WFiIS	1. Dominik Kućma 2. Adam Skorek		Rok 2	Grupa : 2	Zespół: 11
Pracownia Fizyczna 2	Temat: Licznik Geigera - Mullera				Nr ćw. 91
Data wykonania: 28.02.2007	Data oddania: 07.03.2007	Zwrot do poprawy:	Data oddania:	Data zaliczenia:	OCENA:

1. Wyznaczenie charakterystyki licznika Geigera - Mullera

Wyniki pomiarów :

napiecie [V]	1300	1320	1340	1360	1380	1400	1420	1440	1460	1480	1500	1520	1540	1560
zliczenia	309	1046	1040	1050	1047	1032	1035	1051	1024	1060	1090	1056	1048	1083
napiecie [V]	1580	1600	1620	1640	1660	1680	1700	1720	1740	1760	1780	1800	1820	1840
zliczenia	1022	1068	1061	1038	1023	1026	1040	1084	1106	1034	1091	1166	1083	1938

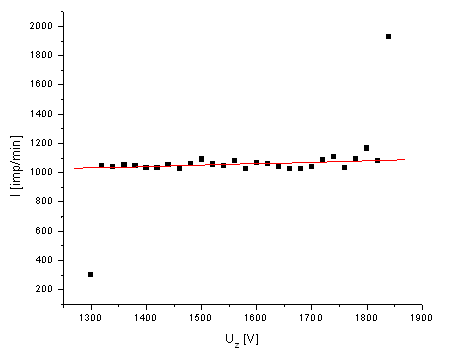
Napięcie progowe (przy którym licznik zaczyna zliczać impulsy) wynosi 1300 V

Za początek plateau przyjmujemy 1320 V, za koniec 1820.

Nachylenie plateau wyznaczamy ze wzoru:

Obliczam nachylenie plateau badając regresję dla punktów pomiarowych

Zatem nachylenie plateau wynosi:

Widzimy, że oba wyniki są zgodne w granicy błędu.

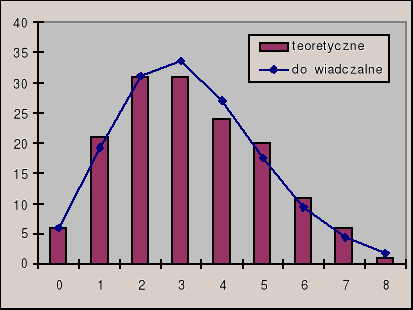
2. Rozkład Poissona

Wykonujemy 148 pomiarów ilości zliczeń licznika w czasie t = 1s

n	k	k*n	P(n)*e	k teoret
0	6	0	1,00	5,96
1	21	21	3,23	19,27
2	31	62	5,22	31,14
3	31	93	5,63	33,54
4	24	96	4,55	27,10
5	20	100	2,94	17,52
6	11	66	1,58	9,44
7	6	42	0,73	4,36
8	1	8	0,30	1,76
suma	151	488

Wartość średnią liczby zliczeń obliczamy ze wzoru:

gdzie N = 151

Wartości teoretyczne obliczamy ze wzoru:

k_teor = NP(n)

gdzie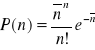

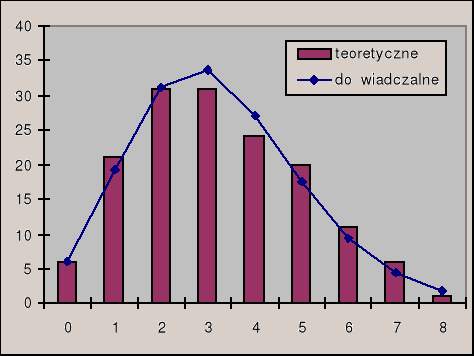
Wyniki doświadczalne oraz teoretyczne zostały przedstawione na wykresie

3. Rozklad Gaussa

Wykonujemy 190 pomiarów ilości zliczeń licznika w czasie t = 4s

n	k	k*n	k(n - n_śr)^2	k teoretyczne
22	1	22	333,4	0,22
23	0	0	0,0	0,34
24	2	48	528,6	0,51
25	1	25	232,8	0,74
26	1	26	203,3	1,05
27	1	27	175,8	1,45
28	2	56	300,5	1,96
29	1	29	126,7	2,59
30	6	180	631,3	3,35
31	3	93	257,1	4,22
32	7	224	477,3	5,20
33	6	198	316,1	6,25
34	4	136	156,6	7,34
35	5	175	138,2	8,41
36	7	252	126,9	9,42
37	15	555	159,2	10,29
38	9	342	45,9	10,99
39	10	390	15,8	11,46
40	19	760	1,3	11,67
41	10	410	5,5	11,60
42	12	504	36,4	11,26
43	9	387	67,7	10,68
44	7	308	98,0	9,89
45	7	315	157,4	8,94
46	11	506	362,7	7,90
47	4	188	181,8	6,81
48	10	480	599,4	5,73
49	8	392	611,4	4,71
50	4	200	379,6	3,79
51	2	102	230,8	2,97
52	2	104	275,8	2,27
53	1	53	162,4	1,70
54	3	162	566,5	1,24

Wartość średnią liczby zliczeń obliczamy ze wzoru:

gdzie N = 190

Wartości teoretyczne obliczamy ze wzoru:

k_teor = NP(n)

gdzie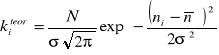

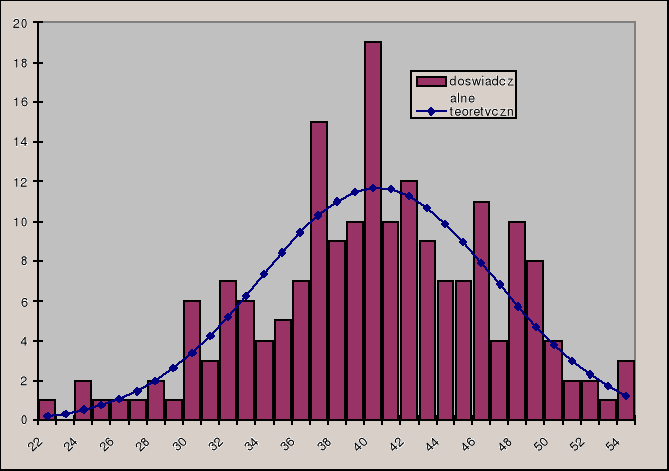
Wyniki doświadczalne oraz teoretyczne zostały przedstawione na wykresie

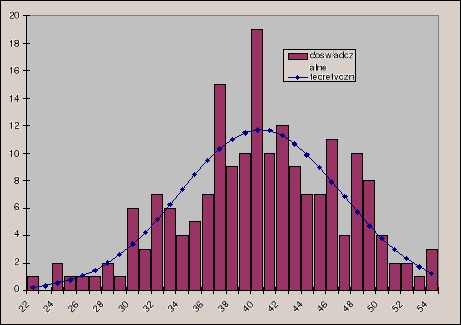
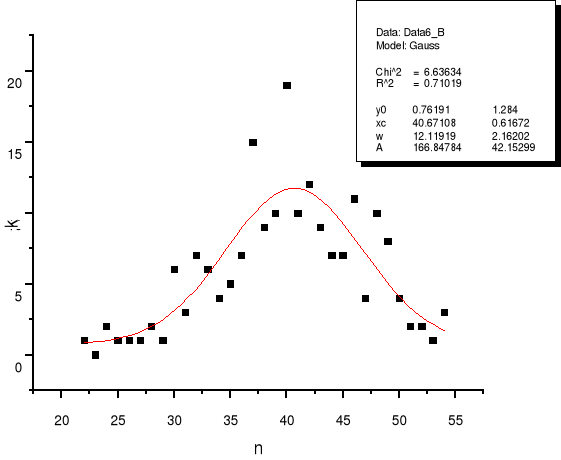
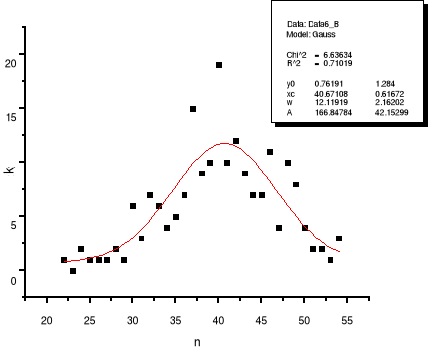
Do punktów pomiarowych dopasowuje krzywą Gaussa w programie Origin:

Widzimy, że wartości średnie wyliczona i dopasowana (40,7+0,6) są równe w granicy błędu. Dużą różnicę odchylenia standardowego należy tłumaczyć innym sposobem liczenia tejże przez program.

Wnioski

Przy wyznaczaniu charakterystyki licznika prawie wszystkie punkty w zakresie plateau można uznać za leżące na jednej prostej (oczywiście w granicach błedu).Jak wynika z wykresu -kąt nachylenia tejze prostej regresji jest rozny od zera.

4. Sprawdzenie testu
dla rozkładu Gaussa:

Wartość X_kryt ² dla stopnia swobody 5 wynosi: 12,59 (poziom ufnosci 0,95) .

Wyznaczona przy pomocy programu Origin wartość testu dla naszych wyników wynosi 6,64.

Zauważamy, że
, zatem obserwowany rozkład nie różni się od normalnego na poziomie ufności 0,95

5. Sprawdzenie testu
dla rozkładu Poissona:

n	k	k*n	P(n)*e	k teoret	Nt=n*pteor	(Nd-Nt)2/Nt
0	6	0	1	5,96	1,32	1,12
1	21	21	3,23	19,27	3,381	1,68
2	31	62	5,22	31,14	22,22	1,20
3	31	93	5,63	33,54	40,3	0,94
4	24	96	4,55	27,1	37,5	2,22
5	20	100	2,94	17,52	26,5	2,05
6	11	66	1,58	9,44	19,992	0,45
7	6	42	0,73	4,36	3,381	4,34
8	1	8	0,3	1,76	1,12	0,65
					suma	14,64

Zauważamy, że
, zatem musimy odrzucić hipotezę, że zaobserwowany rozkład jest rozkładem Poissona.

---