TEMAT ĆWICZENIA:
BADANIE CHARAKTERYSTYKI LICZNIKA GEIGERA-MÜLLERA
I STATYSTYCZNEGO CHARAKTERU ROZPADU PROMIENIOTWÓRCZEGO
1.Wstęp
W wyniku przeprowadzonych badań zostanie określona charakterystyka licznika Geigera-Müllera oraz statystyczny charakter rozkładu promieniotwórczego. Sposób działania licznika GM jest oparty na zasadzie wyładowania lawinowego, powstającego w wyniku wzmacniania procesów jonizacyjnych wywołanych promieniowaniem α, promieniowaniem elektromagnetycznym β lub rentgenowskim X. Jego wielkość nie zależy od energii. Dlatego też licznik GM służy do wykrywania promieniowania a nie określania jego wielkości. W czasie zajęć wykorzystywaliśmy próbkę emitującą promieniowanie beta. Rozkład tego promieniowania można przedstawić następująco:
Na odcinku 90Sr - 90Y rozkład ma postać:
![]()
Wszystkie zjawiska występujące w fizyce jądrowej mają charakter statystyczny. Dlatego podczas pomiarów należy pamiętać, że oprócz niedokładności urządzeń pomiarowych trzeba także uwzględnić odchylenia spowodowane losowością zachodzących procesów.
Do określenia prawdopodobieństwa otrzymania określonej liczby zliczeń stosuje się rozkład prawdopodobieństwa Poissona:
![]()
gdzie:
![]()
- wartość oczekiwana zdarzenia rejestrowanego w stałym czasie t
Rozkład Poissona znajduje zastosowanie w przypadku badania rozpadu promieniotwórczego, ponieważ prawdopodobieństwo rozpadu pojedynczego jądra jest bardzo małe oraz ilość jąder w źródle promieniotwórczym jest bardzo duża.
W przypadku gdy średnia liczba impulsów zliczanych przez licznik Geigera-Müllera jest duża, rozkład Poissona można przybliżyć za pomocą rozkładu Gaussa:
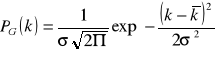
gdzie σ to odchylenie standardowe opisujące rozrzut rejestrowanych wartości impulsów.
2. Układ pomiarowy
Do badania próbki oraz przetwarzania otrzymanych wyników wykorzystywaliśmy:
radiometr wyposażony w sondę Geigera-Müllera
kielichowy licznik Geigera-Müllera
zasilacz prądu zmiennego
komputer z programem Origin.
3. Wykonanie ćwiczenia
1. Pomiar mocy dawki przy użyciu licznika GM przy pomocy cienkiego i grubego okienka mikowego, określenie rodzaju promieniwania
2. Badanie charakterystyki licznika Geigera-Müllera:
wyznaczenie napięcia progowego
wyznaczenie charakterystyki licznika
wyznaczenie obszaru plateau licznika,
określenie Upracy licznika;
3. Badanie statystycznego charakteru rozpadu promieniotwórczego
wykonanie pomiarów przy użyciu programu CWa,
eksport wyników do programu Origin oraz stworzenie wykresów;
4. Opracowanie wyników.
4. Wyniki i ich opracowanie
Pierwszym wykonanym pomiarem był pomiar mocy dawki pochłoniętej przy różnych grubościach okienka licznika Geigera-Müllera:
|
Cienkie okienko |
Grube okienko |
Moc dawki [µGy/h] |
10 |
1,5 |
Z otrzymanych wyników można wywnioskować, że badana próbka emituje promieniowanie beta. Wynika to z tego, iż przy zastosowaniu grubego okienka mikowego większość promieniowania zostało pochłonięte (wyrzucony strumień elektronów został wyhamowany przez okienko licznika).
Kolejnym etapem badania było określenie charakterystyki licznika GM.
Badana próbka została umieszczona w domku pomiarowym. Aby określić napięcie progowe zmniejszaliśmy stopniowo napięcie, aż do momentu gdy impulsy nie były zliczane. Napięcie to jest napięciem progowym ( poniżej tego napięcia nie powstaje wyładowanie lawinowe i impulsy nie są zliczane).
Uprogowe = 435 V
Następnym etapem badania było określenie plateau licznika. W tym celu na początku zostało określone napięcie 720V a następnie było ono zmniejszane. Początkowo co 10V a w miarę zbliżania się do napięcia progowego o coraz mniejsze wartości. Uzyskane wyniki przedstawia poniższa tabela:
U[V] |
720 |
710 |
700 |
690 |
680 |
670 |
660 |
650 |
640 |
630 |
620 |
N[imp] |
1871 |
1968 |
1915 |
1902 |
1946 |
1959 |
1843 |
1902 |
1953 |
1883 |
1827 |
U[V] |
610 |
600 |
590 |
580 |
570 |
562 |
554 |
546 |
538 |
530 |
522 |
N[imp] |
1829 |
1808 |
1851 |
1757 |
1753 |
1691 |
1744 |
1820 |
1749 |
1630 |
1679 |
U[V] |
514 |
506 |
498 |
490 |
484 |
478 |
472 |
466 |
460 |
454 |
448 |
N[imp] |
1630 |
1679 |
1602 |
1688 |
1539 |
1599 |
1578 |
1500 |
1546 |
1518 |
1521 |
U[V] |
445 |
442 |
439 |
436 |
|
|
|
|
|
|
|
N[imp] |
1308 |
927 |
343 |
4 |
|
|
|
|
|
|
|
Uzyskane wyniki zostały przeniesione do programu Origin i za jego pomocą uzyskaliśmy następujący wykres:
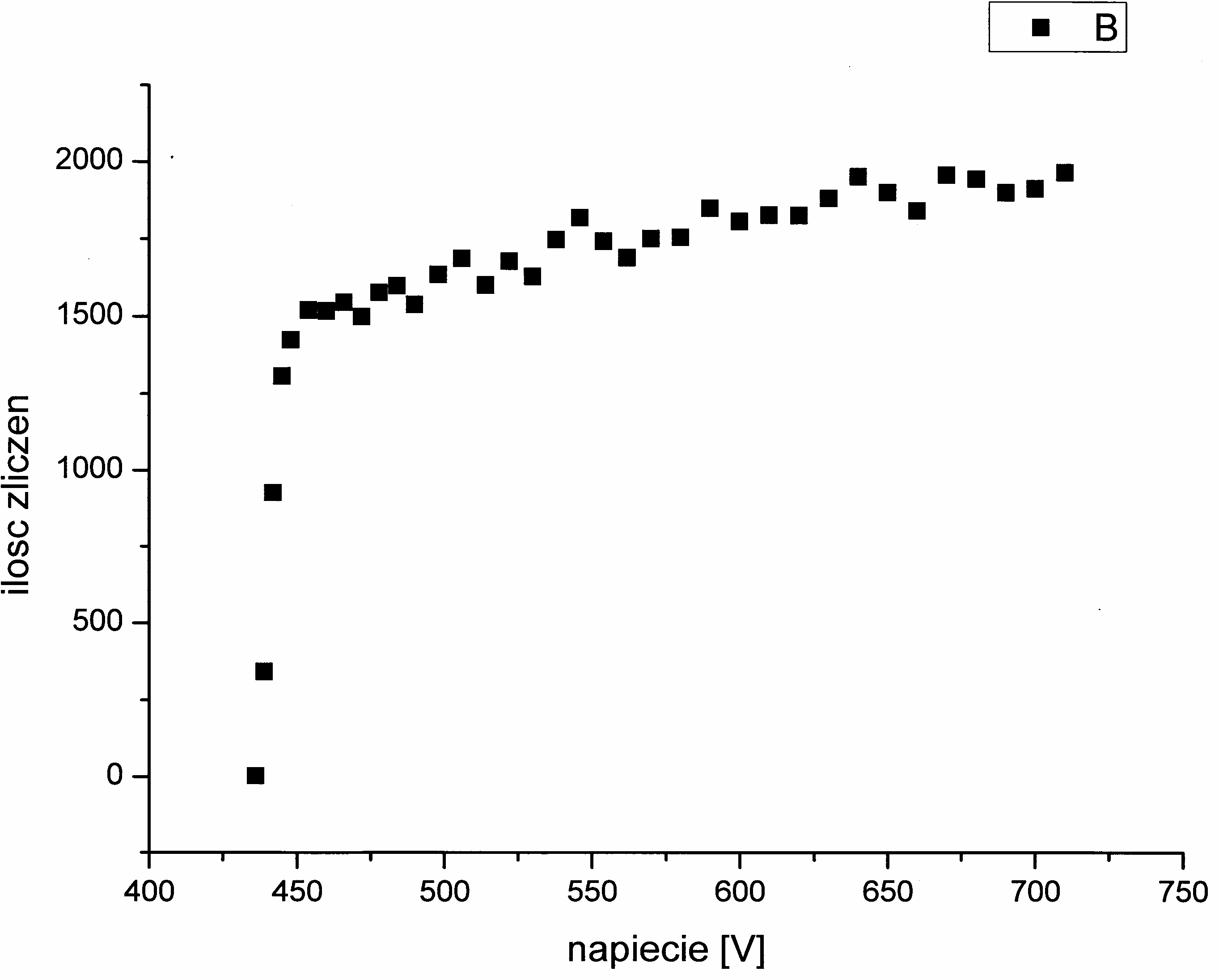
Na Na podstawie otrzymanych wyników określiliśmy obszar plateau:
U1 = 454 V,
U2 = 720 V.
Długość plateau wynosi:
U2 - U1 =720-454=266V
Napięcie pracy licznika znajduje się poprzez określenie środka plateau. A więc:
![]()
W naszym przypadku jest to:
![]()
Następnym parametrem jaki należy sprawdzić w liczniku GM jest nachylenie plateau. Obliczamy je z następującego wzoru:

Gdzie:
I1,I2 to ilości impulsów odpowiadające napięciom U1 i U2
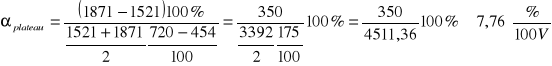
5. Rachunek błędów
Ze względu na to, iż używaliśmy przyrządów cyfrowych błędy obliczymy korzystając z następujących wzorów:
![]()
![]()
Po podstawieniu do wzorów:
![]()
![]()
![]()
![]()
Błąd plateau obliczamy korzystając z następującego wzoru:
![]()
plateau = 7,76 0,06 [%/100V]
6. Badanie statystycznego charakteru rozpadu promieniotwórczego
W celu ukazania statycznego charakteru rozpadu promieniotwórczego w domku pomiarowym zostały umieszczone dwie próbki. Następnie przy pomocy programu CW1a dokonaliśmy 1000 pomiarów co 0,1s. Następnie uzyskane wyniki wyeksportowaliśmy do programu Origin i za jego pomocą stworzyliśmy histogram. Przedstawia on ilość zliczeń dla każdej zmiennej losowej. Do uzyskanego histogramu dopasowaliśmy wykres Gaussa.
Prawdopodobieństwo doświadczalne obliczamy z następującego wzoru:
![]()
gdzie:
k = 40,
n(k) = 94,
n = 1500,
![]()
Określenie prawdopodobieństwa przy pomocy rozkładu Gaussa:
Wzór matematyczny na rozkład Gaussa:
![]()
Po przyrównaniu do niego wzoru z programu origin otrzymujemy:
![]()
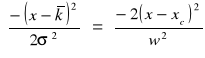
![]()
![]()
Prawdopodobieństwo uzyskania poszukiwanej liczby zliczeń:
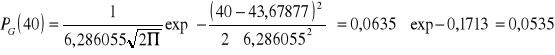
7. Wnioski
Przeprowadzone badanie na początku dowiodło, że badana próbka emituje promieniowanie β. Wynika to z tego, iż przy zastosowaniu grubego okienka mikowego większość promieniowania została pochłonięta. W przypadku pracy z próbką emitującą promieniowanie β należy stosować osłony o małej liczbie atomowej, dzięki czemu wytwarzane podczas tłumienia promieniowanie rentgenowskie będzie miało małe natężenie. Dalsze badania udowodniły zgodność opisu teoretycznego z rzeczywistym licznika GM. Uzyskane nachylenie plateau ok. 7,5 [%/100V] może potwierdza teorię zgodnie, z którą nie powinno ono przekraczać kilku procent. Następne badania potwierdziły statystyczny charakter rozpadu promieniotwórczego. W wyniku zwiększania ilości próbek w domku pomiarowym uzyskiwany wykres przesuwał się w prawą stronę. Działo się tak na skutek zwiększani impulsów w jednostce czasu.
![]()
T1/2 = 28 lat
![]()
Emax = 2,27 MeV
Emax = 0,546 MeV
90Zr
90Sr
90Y
Z
40
39
38

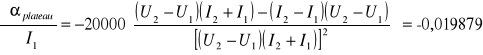
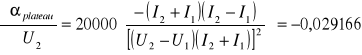
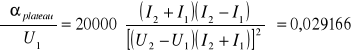
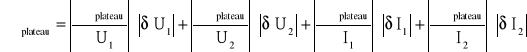
Wyszukiwarka
Podobne podstrony:
ĆWICZENIE 501, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Ćwiczenie 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i b
ĆWICZENIE 501LAST, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
fiza2, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i badanie
Poprawa sprawozdania kwant gamma cw 15, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka l
Ćwiczenie 1 2, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Sprawozdanie nr 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
Sprawko - Licznik Geigera-Mullera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka liczni
LAB 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i badanie
LF 2 lab 4 +wiczenie 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-
1-licznik geigera-mullera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geige
Geigeiron, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i bad
Badanie charakterystyki licznika Geigera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka
+wiczenie1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i ba
Spraw1fizlab, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Lab.Fiz II-1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
sprawoad[1].betti, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
Rozkład doświadczalny 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera
więcej podobnych podstron