LABORATORIUM FIZYKI II |
Ćwiczenie nr 1 |
|
Badanie charakterystyki licznika Geigera - Mullera i statystycznego charakteru rozpadu promieniotwórczego. |
||
Nazwisko i imię |
Karabin Maciej |
|
Grupa/zespół |
Grupa 2.2 Wydział Inżynierii Materiałowej / zespół 2 |
|
Data |
20.10.2008 |
|
Badanie charakterystyki licznika Geigera - Mullera i statystycznego charakteru rozpadu promieniotwórczego.
Wstęp.
Celem ćwiczenia było zapoznanie się z budową oraz zasadą działania licznika Geigera - Mullera oraz wyznaczenie charakterystyk dla urządzenia użytego w doświadczeniu. Zadaniem zespołu było także zidentyfikowanie próbki materiału promieniotwórczego oraz wykazanie, że proces rozpadu promieniotwórczego ma charakter statystyczny,który da się opisać rozkładami Gaussa i Poissona.
Układ pomiarowy.
Układ pomiarowy składał się z licznika Geigera-Mullera zamontowanego na pojemniku z preparatem promieniotwórczym. Układ połączony był z zasilaczem (niezbędnym do działania radiometru) oraz z komputerem zliczającym liczebność impulsów.
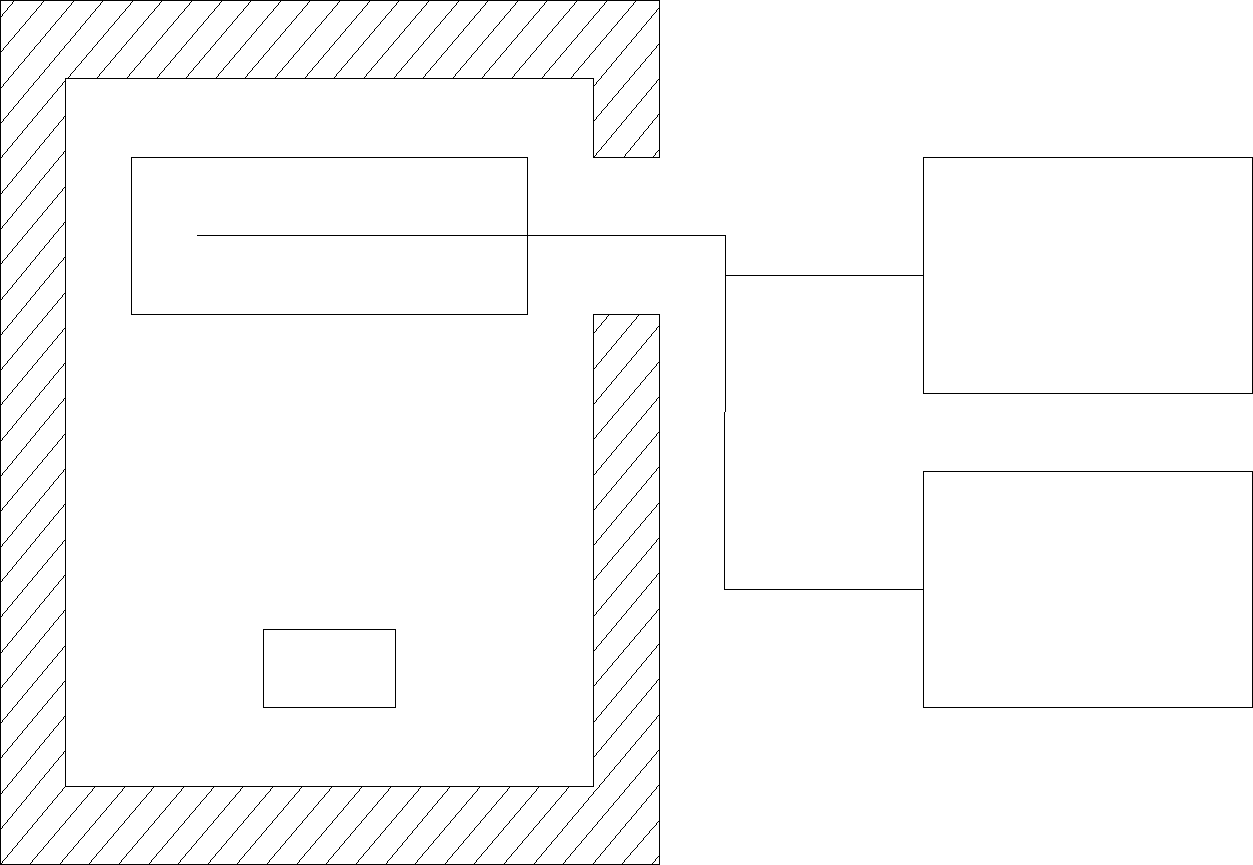
Przebieg ćwiczenia.
Zidentyfikowanie próbki (określenie rodzaju promieniowania).
Pomiar charakterystyki licznika Geigera - Mullera.
Badanie statystycznego charakteru rozpadu promieniotwórczego.
Wykonanie ćwiczenia.
Identyfikacja próbki:
Pomiar wykonano przy pomocy licznika Geigera - Mullera wykorzystując cienkie i grube okno radiometru. Uzyskano wyniki 125 [μGy/h] dla okna cienkiego oraz 5 [μGy/h] dla okna grubego. Otrzymane wyniki mogą sugerować, że badacz ma do czynienia z emisją strumienia elektronów (rozpad β-). Wartość dawki dla cząstki gamma byłaby z pewnością większa, gdyż cząstka ta jest bardziej przenikliwa oraz powoduje powstawanie elektronów wtórnych na obudowie licznika co zwiększyłoby wskazania. Dodatkowym spostrzeżeniem był fakt iż osłony urządzeń wykonane są ze szkła, które pochłania promieniowanie beta a nie pochłania promieniowania alfa.
Okazało się, że badana próbka faktycznie emitowała strumień elektronów (promieniowanie β):
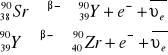
Pomiar charakterystyki licznika Geigera - Mullera.
Dla różnych wartości napięcia wykonano następującą charakterystykę:
U[V] |
I [imp/10s] |
U[V] |
I [imp/10s] |
720 |
2479 |
560 |
2161 |
715 |
2509 |
555 |
2165 |
711 |
2440 |
547 |
2197 |
706 |
2453 |
539 |
2062 |
702 |
2515 |
528 |
2155 |
697 |
2461 |
522 |
2081 |
693 |
2506 |
517 |
2077 |
689 |
2466 |
513 |
2094 |
684 |
2439 |
509 |
2193 |
678 |
2391 |
505 |
2104 |
675 |
2312 |
503 |
2095 |
670 |
2452 |
498 |
2068 |
665 |
2363 |
494 |
1992 |
659 |
2382 |
489 |
2031 |
655 |
2438 |
484 |
2108 |
651 |
2335 |
481 |
2029 |
646 |
2401 |
475 |
1949 |
642 |
2390 |
472 |
1970 |
637 |
2337 |
467 |
1967 |
633 |
2374 |
465 |
1930 |
628 |
2259 |
460 |
1902 |
623 |
2420 |
455 |
1906 |
616 |
2478 |
452 |
1886 |
610 |
2361 |
447 |
1907 |
603 |
2320 |
444 |
1835 |
593 |
2287 |
440 |
1769 |
587 |
2335 |
436 |
1427 |
581 |
2334 |
431 |
604 |
572 |
2294 |
429 |
103 |
566 |
2240 |
428 |
8 |
Na podstawie pomiarów sporządzony został wykres:
Z wykresu odczytana została orientacyjna wartość napięcia progowego oraz wartości napięć początku plateau i końca plateau charakterystyki:
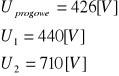
Na podstawie tych danych policzone zostało napięcie pracy licznika:
![]()
Policzono także długość plateau:
![]()
oraz nachylenie plateau αplateau:
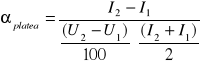
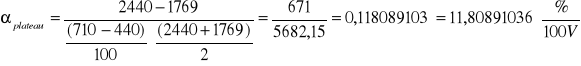
Rachunek błędu:
Wyznaczenie błędu systematycznego pomiaru napięcia:
Błąd wyznaczamy w sposób następujący:
δU1=0,3% mierzonej wielkości + 1/2 ostatniej cyfry = 440×0,003 + 0 = 1,32 [V]
δU2=0,3% mierzonej wielkości + 1/2 ostatniej cyfry = 710×0,003 + 0 = 2,13 [V]
Ostateczny wynik pomiaru to:
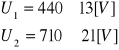
Obliczono błąd systematyczny zliczeń liczby impulsów I1 i I2 zgodnie ze wzorem:
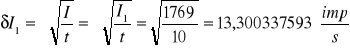
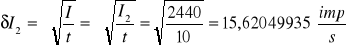
Ostateczny wynik to:
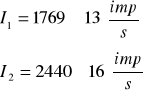
Błąd systematyczny wyznaczenia nachylenia ![]()
obliczony został metodą różniczki zupełnej:
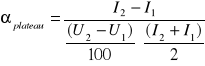
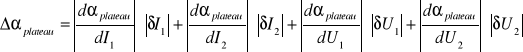
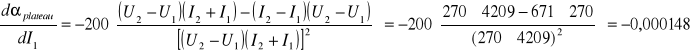

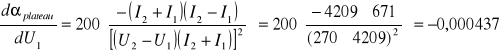
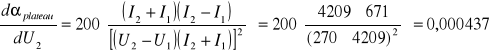
![]()
![]()
Ostateczny wynik:
![]()
Badanie statystycznego charakteru rozpadu promieniotwórczego:
Obserwację rozpadu promieniotwórczego jako funkcji statystycznej dokonano za pomocą licznika Geigera - Mullera umieszczonego nad próbką oraz programu zliczającego ilość impulsów w czasie.
Wyniki pomiaru (k oraz n(k))zostały zapisane w pliku tekstowym MK2 a następnie na ich podstawie policzono prawdopodobieństwa doświadczalne oraz prawdopodobieństwa wynikające z rozkładu Gaussa i rozkładu Poissona.
k |
n(k) |
P(k) |
k(p)k |
k^2p(k) |
Pp(k) |
Np(k) |
Xp(k) |
x |
pg(x) |
Pg(k) |
Xg |
Xg(k) |
6 |
1 |
0,00 |
0,01 |
0,0 |
0,00 |
0 |
0,61 |
-2,8 |
0,01 |
0,00 |
2 |
0,3 |
7 |
2 |
0,00 |
0,01 |
0,1 |
0,00 |
1 |
0,46 |
-2,6 |
0,01 |
0,00 |
3 |
0,4 |
8 |
3 |
0,00 |
0,02 |
0,2 |
0,00 |
3 |
0,00 |
-2,4 |
0,02 |
0,01 |
6 |
1,1 |
9 |
7 |
0,01 |
0,06 |
0,6 |
0,01 |
6 |
0,16 |
-2,1 |
0,04 |
0,01 |
9 |
0,5 |
10 |
20 |
0,02 |
0,20 |
2,0 |
0,01 |
11 |
6,92 |
-1,9 |
0,06 |
0,01 |
14 |
2,4 |
11 |
24 |
0,02 |
0,26 |
2,9 |
0,02 |
19 |
1,33 |
-1,7 |
0,10 |
0,02 |
21 |
0,4 |
12 |
34 |
0,03 |
0,41 |
4,9 |
0,03 |
29 |
0,69 |
-1,5 |
0,14 |
0,03 |
30 |
0,5 |
13 |
43 |
0,04 |
0,56 |
7,3 |
0,04 |
42 |
0,01 |
-1,2 |
0,18 |
0,04 |
40 |
0,2 |
14 |
46 |
0,05 |
0,64 |
9,0 |
0,06 |
56 |
1,88 |
-1,0 |
0,24 |
0,05 |
52 |
0,7 |
15 |
61 |
0,06 |
0,92 |
13,7 |
0,07 |
70 |
1,14 |
-0,8 |
0,29 |
0,06 |
64 |
0,1 |
16 |
71 |
0,07 |
1,14 |
18,2 |
0,08 |
81 |
1,35 |
-0,6 |
0,34 |
0,07 |
74 |
0,2 |
17 |
91 |
0,09 |
1,55 |
26,3 |
0,09 |
89 |
0,03 |
-0,4 |
0,37 |
0,08 |
83 |
0,8 |
18 |
91 |
0,09 |
1,64 |
29,5 |
0,09 |
93 |
0,03 |
-0,1 |
0,39 |
0,09 |
87 |
0,1 |
19 |
97 |
0,10 |
1,84 |
35,0 |
0,09 |
91 |
0,42 |
0,1 |
0,40 |
0,09 |
88 |
0,9 |
20 |
80 |
0,08 |
1,60 |
32,0 |
0,08 |
85 |
0,26 |
0,3 |
0,38 |
0,08 |
84 |
0,2 |
21 |
71 |
0,07 |
1,49 |
31,3 |
0,08 |
75 |
0,23 |
0,5 |
0,35 |
0,08 |
77 |
0,5 |
22 |
67 |
0,07 |
1,47 |
32,4 |
0,06 |
64 |
0,17 |
0,7 |
0,30 |
0,07 |
67 |
0,0 |
23 |
52 |
0,05 |
1,20 |
27,5 |
0,05 |
52 |
0,00 |
1,0 |
0,25 |
0,06 |
55 |
0,2 |
24 |
41 |
0,04 |
0,98 |
23,6 |
0,04 |
40 |
0,02 |
1,2 |
0,20 |
0,04 |
44 |
0,2 |
25 |
32 |
0,03 |
0,80 |
20,0 |
0,03 |
30 |
0,15 |
1,4 |
0,15 |
0,03 |
33 |
0,0 |
26 |
25 |
0,03 |
0,65 |
16,9 |
0,02 |
21 |
0,59 |
1,6 |
0,11 |
0,02 |
23 |
0,1 |
27 |
12 |
0,01 |
0,32 |
8,7 |
0,01 |
15 |
0,53 |
1,9 |
0,07 |
0,02 |
16 |
1,0 |
28 |
12 |
0,01 |
0,34 |
9,4 |
0,01 |
10 |
0,47 |
2,1 |
0,05 |
0,01 |
10 |
0,3 |
29 |
3 |
0,00 |
0,09 |
2,5 |
0,01 |
6 |
1,75 |
2,3 |
0,03 |
0,01 |
6 |
1,8 |
30 |
7 |
0,01 |
0,21 |
6,3 |
0,00 |
4 |
2,39 |
2,5 |
0,02 |
0,00 |
4 |
2,8 |
31 |
2 |
0,00 |
0,06 |
1,9 |
0,00 |
2 |
0,06 |
2,7 |
0,01 |
0,00 |
2 |
0,0 |
32 |
3 |
0,00 |
0,10 |
3,1 |
0,00 |
1 |
1,91 |
3,0 |
0,01 |
0,00 |
1 |
3,2 |
33 |
0 |
0,00 |
0,00 |
0,0 |
0,00 |
1 |
0,78 |
3,2 |
0,00 |
0,00 |
1 |
0,6 |
34 |
0 |
0,00 |
0,00 |
0,0 |
0,00 |
0 |
0,43 |
3,4 |
0,00 |
0,00 |
0 |
0,3 |
35 |
1 |
0,00 |
0,04 |
1,2 |
0,00 |
0 |
2,62 |
3,6 |
0,00 |
0,00 |
0 |
6,1 |
36 |
1 |
0,00 |
0,04 |
1,3 |
0,00 |
0 |
6,61 |
3,8 |
0,00 |
0,00 |
0 |
16,2 |
Σ |
1000 |
|
|
Σ=368 |
σ=4,52 |
|
Σ=34 |
|
|
|
|
Σ=42 |
Na podstawie danych zamieszczonych w tabeli, które zostały przeliczone na potrzeby rozkładów Gaussa i Poissona sporządzony został wykres:
Dla wyznaczonych punktów wartości prawdopodobieństwa wynoszą odpowiednio:
Dla k=17:
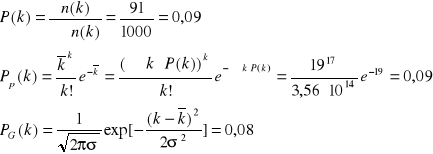
Dla k=23:
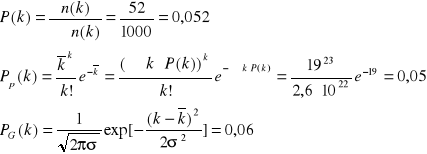
Wnioski
W ćwiczeniu została wyznaczona charakterystyka licznika Geigera - Mullera. Niestety na wykreślonym wykresie nie jest widoczna górna granica plateau charakterystyki. Mogło to być spowodowane niedokładnością pomiaru w punktach przegięcia wykresu. Dlatego też wartość górnej granicy plateau została wyznaczona dosyć orientacyjnie.
W doświadczeniu udało się także udowodnić, że rozpad promieniotwórczy ma charakter statystyczny. Oznacza to, że możliwe jest tylko wyznaczenie prawdopodobieństwa, z jakim zajdzie dana przemiana.. Na wykresie widać doskonale jak zbliżone są rozkład Gaussa i Poissona do rozkładu uzyskanego drogą eksperymentalną. Także prawdopodobieństwa wyliczone na trzy sposoby nie różnią się od siebie znacznie.
Zasilacz
Radiometr
Geigera - Mullera
Licznik impulsów
Osłona ochronna licznika
Preparat promieniotwórczy
Wyszukiwarka
Podobne podstrony:
ĆWICZENIE 501, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Ćwiczenie 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i b
LABORATORIUM FIZYKI cw1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera
ĆWICZENIE 501LAST, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
fiza2, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i badanie
Poprawa sprawozdania kwant gamma cw 15, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka l
Ćwiczenie 1 2, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Sprawozdanie nr 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
Sprawko - Licznik Geigera-Mullera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka liczni
LAB 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i badanie
LF 2 lab 4 +wiczenie 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-
1-licznik geigera-mullera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geige
Geigeiron, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i bad
+wiczenie1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i ba
Spraw1fizlab, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Lab.Fiz II-1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
sprawoad[1].betti, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
Rozkład doświadczalny 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera
więcej podobnych podstron