Politechnika Warszawska

2003

Laboratorium Fizyki II

Sprawozdanie

TEMAT: Badanie charakterystyki licznika Geigera-Mullera i statystycznego charakteru rozpadu promieniotwórczego.

AUTOR: Beata Pachniewicz

Zespół 6

WIP PO-71

1. Cel ćwiczenia.

Podstawowym zadaniem realizowanym podczas tego ćwiczenia było badanie charakteru promieniowania jonizującego, a ściślej stochastycznej natury promieniowania β. Wśród aparatury wykorzystywanej przy wykonywaniu ćwiczenia wymienić trzeba przede wszystkim licznik Geigera-Mullera oraz komputer PC, na którym następowała obróbka uzyskanych danych.

2. Budowa licznika Geigera-Mullera

Licznik G-M zbudowany jest z dwóch elektrod: cylindrycznej katody i umieszczonej wzdłuż jej osi i odizolowanej nici - anody. Całość jest szczelnie zamknięta i wypełniona gazem pod zmniejszonym ciśnieniem. Ciśnienie dobierane jest tak, by droga swobodna elektronów była mała w stosunku do wymiarów licznika. Przebiegające przez obszar licznika promienie (α, β, γ ) lub neutrony jonizują na swej drodze cząsteczki gazu. Tak otrzymane jony przyspieszane silnym polem elektrycznym rozpędzają się. W wyniku ich zderzeń z atomami obojętnymi następuje jonizacja kolejnych atomów, co prowadzi do jonizacji lawinowej i w konsekwencji przepływu prądu. Prąd ten maleje bardzo szybko, ponieważ w czasie jego przepływu spada gwałtownie napięcie na dołączonym do obwodu oporze R. Tym samym spada natężenie pola wewnątrz licznika, na skutek czego przerwany zostaje proces jonizacji lawinowej. Wyładowanie lawinowe może być również przerwane (wygaszone) dzięki zastosowaniu w komorze licznika odpowiedniej mieszaniny gazów (liczniki samogasnące). Przerwanie wyładowania lawinowego jest nieodzowne, ażeby licznik mógł zarejestrować przejście kolejnej cząstki. Czas wygaszania wyładowania jest bardzo krótki (rzędu 10^-4 s), jednak proces ten nie jest natychmiastowy. Ze skończonością tego czasu związany jest tzw. czas martwy licznika, czyli czas, w którym licznik nie jest zdolny do zadziałania pod wpływem nowej cząstki jonizującej.

Prawidłowość pracy licznika zależy od wartości przyłożonego napięcia - przy zbyt niskim napięciu jonizacja lawinowa nie rozwija się i licznik nie działa. Napięcie, poniżej którego impulsy nie są zliczane nazywamy napięciem progowym U_p. Z kolei po przekroczeniu pewnego napięcia granicznego U₂ dochodzi do zbyt dużego wzmocnienia gazowego i liczba rejestrowanych impulsów wzrasta bardzo szybko, lecz są to impulsy zdublowane lub nawet uwielokrotnione. Pomiędzy napięciem progowym i granicznym występuje obszar tzw. plateau, w zakresie pracy którego licznik rejestruje ponad 99% dostających się do niego cząsteczek naładowanych. W obszarze plateau, którego nachylenie nie powinno przekraczać 2-3%, znajduje się napięcie pracy licznika.

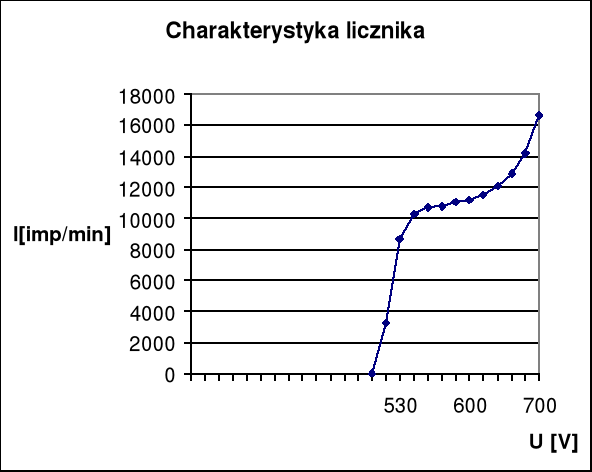
Krzywa w układzie napięcie - szybkość zliczania impulsów otrzymana przy stałym natężeniu promieniowania nazywa się charakterystyką roboczą licznika i jest jego podstawowym parametrem. Przebieg typowej charakterystyki licznika G-M przedstawia poniższy rysunek:

3. Badanie charakterystyki licznika Geigera-Mullera

Podstawowe znaczenie przy badaniu charakterystyki roboczej licznika G-M ma wyznaczenie:

1. napięcia pracy

2. długości plateau

3. nachylenia plateau

ad. a)

Dokonując pomiarów szybkości zliczania impulsów dla różnych napięć określono U_p (napięcie, przy którym licznik rozpoczął zliczanie) oraz U₁ i U₂, gdzie U₁ i U₂ odpowiednio - początek i koniec plateau. Wyboru U₁ oraz U₂ dokonano w sposób arbitralny, korzystając z wyników zamieszczonych w protokole pomiarowym.

Jako napięcie pracy licznika przyjęto:

U_robocze = (U₁+U₂)/2

gdzie U_p= 526 [V]; U₁ = 540 [V]; U₂= 660 [V]

czyli U_robocze = 600 [V]

U[V]	N[imp]	I[imp/min]	σ=√I/t
700	16655	16655	129,1
680	14190	14190	119,1
660	12908	12908	113,6
640	12049	12049	109,8
620	11515	11515	107,3
600	11182	11182	105,7
580	11075	11075	105,2
560	10740	10740	103,6
550	10691	10691	103,4
540	10279	10279	101,39
530	8679	8679	93,16
526	3243	3243	56,9

ad. b)

Określenie początku i końca plateau jest równoznaczne z wyznaczeniem jego długości d:

d = U₂ -U₁= 120 [V]

ad. c)

Wyznaczenie nachylenia plateau polega na znalezieniu nachylenia prostej aproksymującej charakterystykę roboczą licznika, która w zakresie pomiędzy U₁ i U₂ przedstawiona jest za pomocą 14 punktów.

4. Wyznaczanie czasu martwego i tła licznika

Przy dostatecznie dużej szybkości liczenia szybkość zarejestrowanych impulsów I jest mniejsza od rzeczywistej Io. Liczba zgubionych w jednostce czasu impulsów równa jest rzeczywistej ilości zliczeń na jednostkę czasu Io pomnożonej przez ułamek czasu, w ciągu którego licznik jest martwy. A zatem:

Io = I +Io* (I*τ)

lub:

Io = I/(1-I*τ)

gdzie:

τ - czas martwy licznika

Podane wyżej wzory pozwalają wyznaczyć czas martwy licznika przy założeniu, że dysponujemy wartościami Io i I. Wobec faktu, że jedyną wartością daną jest wartość I, do wyznaczenia czasu martwego licznika konieczne jest ułożenie równania (równań) pomocniczego. W tym celu wykorzystujemy zależność:

Io_1,2 = Io₁ + Io₂

lub:

I₁₂/(1-I₁₂*τ) = I₁/(1-I₁*τ)+ I₂/(1-I₂*τ)

Rozwiązanie tego równania względem τ (z pominięciem małych wyższego rzędu) pozwala zapisać:

(1)

nr preparatu	t [min]	N [imp]	IN [imp/min]	I = IN - ITł
1	3	31547	10515,7	10499,7
1+2	3	72507	24169	24153
2	3	45207	15069	15053

Podstawiając do wzoru (1) wartości z tabeli otrzymuję:

τ = 3,72*10^-3 [s]

Ponieważ każdy licznik rejestruje impulsy wywołane promieniowaniem kosmicznym, a także zlicza cząstki β z materiałów konstrukcyjnych konieczne jest dla zachowania dokładności pomiarowej licznika wyznaczenie jego tła (t). Definiowane jest ono jako ilość impulsów jaką rejestruje licznik (w jednostce czasu) przy braku preparatów w komorze.

t = 16 [imp/min]

5. Badanie statystycznego charakteru promieniowania

Wyznaczenie charakterystyki licznika G-M, a w szczególności napięcia pracy U_robocze pozwala rozpocząć badanie statystycznego charakteru promieniowania.

Z punktu widzenia statystyki matematycznej grupa atomów stanowi zbiór jednakowych elementów. Każdemu elementowi przyporządkowane jest prawdopodobieństwo p(t) wystąpienia zdarzenia losowego (zajścia przemiany promieniotwórczej) oraz prawdopodobieństwo q(t) nie wystąpienia zdarzenia czyli przeżycia. Ponieważ obydwa zdarzenia są rozłączne zatem q(t) + p(t) =1. Prawdopodobieństwo obserwacji k zdarzeń w zbiorze N elementowym określa rozkład dwumianowy.

Zasadniczym problemem przy wyznaczaniu prawdopodobieństwa określonego rozkładem dwumianowym jest znalezienie liczby N atomów. W praktyce, w badaniach jąder atomowych, niezmiernie trudno jest dysponować próbkami o dokładnie określonej liczbie atomów. Ponieważ jednak w próbkach o masie rzędu grama znajduje się 10²¹-10²³ atomów liczbę N można traktować jako nieskończenie dużą. W takim przypadku do opisu rozkładu prawdopodobieństwa zajścia k przemian promieniotwórczych można użyć aproksymacji rozkładu dwumianowego - rozkładu Gaussa lub rozkładu Poissona. Obydwa rozkłady nie wymagają już znajomości N. Dla rozkładu Gaussa, który stosuje się dla większych k (w rozpatrywanym przykładzie dla k> 20) konieczne jest określenie dwóch parametrów k_śr oraz odchylenia standardowego. Do wyznaczenia rozkładu Poissona (dla k <20 ) wystarcza znajomość k_śr.

W realnym fizycznym eksperymencie niemożliwe jest jednak spełnienie warunków wymaganych dla wyznaczenia rzeczywistej wartości średniej, co wynika ze skończonej ilości pomiarów (z).

Rozwiązaniem jest zastąpienie k_śr. wartością zdefiniowaną jako:

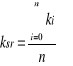
gdzie n - liczba pomiarów

W rezultacie n - krotnego powtarzania pomiaru jednej próbki (przy napięciu roboczym U_robocze) otrzymuje się rozkład doświadczalny zobrazowany w postaci histogramu. Wielokrotne badanie tej samej próbki uzasadnione jest tym, że liczba przemian jest niewielka (co wynika z niskiej wartości stałej rozpadu) i zachowany jest warunek N ≈ ∞, a ilość atomów mogących przemienić się w czasie pojedynczego pomiaru jest w przybliżeniu stała.

Otrzymane rozkłady w sposób oczywisty różnią się od rozkładów rzeczywistych. Wynika to z faktu dokonania tylko odpowiednio 1000 pomiarów. Posługując się testem χ² można dokonać pomiaru tych rozbieżności.

	Rozkład doświadczalny				Rozkład Poissona		Rozkład Gaussa
A	B	C	D	E	F	G	H	I
k	n(k)	B/n	A*C	A*A*C	P1(k)	F*n	P2(k)	H*n
0	5	0,004167	0	0	0,001692	2,030083	0,01267	15,20445
1	10	0,008333	0,008333	0,008333	0,010797	12,95599	0,025161	30,19298
2	36	0,03	0,06	0,12	0,034452	41,34257	0,044464	53,35674
3	72	0,06	0,18	0,54	0,073291	87,94943	0,069926	83,91132
4	103	0,085833	0,343333	1,373333	0,116936	140,3233	0,097863	117,4356
5	137	0,114167	0,570833	2,854167	0,149257	179,1087	0,121884	146,2604
6	172	0,143333	0,86	5,16	0,15876	190,5119	0,135089	162,1071
7	152	0,126667	0,886667	6,206667	0,144744	173,6924	0,133243	159,8914
8	141	0,1175	0,94	7,52	0,115469	138,5631	0,116954	140,3447
9	89	0,074167	0,6675	6,0075	0,081881	98,25667	0,091355	109,6264
10	48	0,04	0,4	4	0,052256	62,7074	0,063504	76,20473
11	16	0,013333	0,146667	1,613333	0,030318	36,3817	0,039284	47,14079
12	10	0,008333	0,1	1,2	0,016124	19,349	0,021626	25,95133
13	5	0,004167	0,054167	0,704167	0,007916	9,49887	0,010595	12,71366
14	1	0,000833	0,011667	0,163333	0,003608	4,330128	0,004619	5,5428
45	2	0,001667	0,075	3,375	2,36E-23	2,84E-20	2,31E-39	2,78E-36
16	0	0	0	0	0,000612	0,734857	0,000619	0,74249
17	1	0,000833	0,014167	0,240833	0,00023	0,275874	0,00019	0,228136

Liczebność serii pomiarowej n=1000

Odchylenie standardowe σ = 6,2755

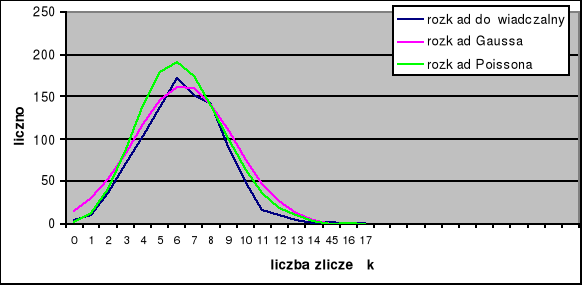
Porównanie wykresu doświadczalnego z rozkładem Gaussa i rozkładem Poissona:

4. Wnioski

Na podstawie pomiarów liczby zliczeń zarejestrowanych w jednostce czasu wyznaczona została charakterystyka robocza licznika. Pamiętać należy o tym, że uzyskane wartości mają w znacznym stopniu charakter przybliżony. Wynika to po części z niedokładności samej aparatury (podziałka elementarna licznika = 2V), oraz, w przypadku określania napięcia roboczego i nachylenia plateau, z arbitralnego wyboru punktów krańcowych. Uzyskana wartość nachylenia plateau - kilkakrotnie większa niż wartość uważana za prawidłową w dobrych licznikach - jest właśnie wynikiem takiego, a nie innego wyboru punktów krańcowych. Jak łatwo zauważyć na wykresie 2, kosztem ograniczenia długości plateau możliwe byłoby zmniejszenie jego nachylenia. Krok ten jednak pociągałby za sobą „wypadnięcie” poza zakres długości plateau uznawanych za dobre.

Analiza czasu martwego licznika pozwala sądzić, że licznik pracuje poprawnie, a uzyskany rząd wielkości (10^-3 s) zgadza się z wartością postulowaną. Poziom tła licznika jest jednocześnie na tyle mały, że nie zakłóca on w znaczący sposób obliczonego czasu, a zatem korekta liczby zliczeń o poziom tła nie jest konieczna. Uwzględniając pewną arbitralność wyboru napięcia progowego można przyjąć, iż również w tym przypadku korekta U_p ze względu ma tło licznika nie jest celowa.

Dane otrzymane w wyniku 1000- krotnego pomiaru tej samej próbki wskazują, że rozpad promieniotwórczy ma naturę stochastyczną. Aby to wykazać zrobiliśmy na zajęciach histogramy. Nie znając całkowitej liczby atomów nie możemy stosować rozkładu dwumianowego dlatego najlepszym wyjściem jest zastosowanie rozkładu Gaussa lub Poissona bowiem one nie wymagają znajomości całkowitej liczby atomów. Poprzez analizę wykresów możemy już stwierdzić, że lepszy byłby rozkład Gaussa gdyż dla mojej próbki k_śr=6,322

---