Łukasz Jońca
Zespół 4
Grupa 2.2
WIM
Ćw. 1. Badanie charakterystyki licznika Geigera-Müllera i statystycznego rozpadu promieniotwórczego
1. Wstęp
Celem ćwiczenia było wyznaczenie charakterystyki licznika GM oraz zbadanie statystycznego charakteru rozpadu promieniotwórczego. Licznik GM jest detektorem promieniowania beta, a także gamma i X. Fotony gamma i X są wykrywane pośrednio, dzięki wybijaniu elektronów wtórnych z obudowy licznika.
2. Układ pomiarowy
W badaniu korzystano z kielichowego licznika GM. Licznik taki składa się z metalowej obudowy w kształcie cylindra oraz cienkiego drutu znajdującego się w jego osi. Pierwszy element pełni rolę katody, zaś drugi - anody. Aparat wypełniony jest argonem pod zmniejszonym ciśnieniem. Dodatkowym elementem układu jest cienkie mikowe okienko umożliwiające rejestrację cząstek beta.
Schemat licznika
Licznik GM służy jedynie do wykrywania obecności cząstek jonizujących, nie mówi jednak nic o energiach tych cząstek ze względu na pojawiające się wyładowanie lawinowe.
3. Przebieg ćwiczenia
- przeprowadzono pomiar mocy dawki źródła promieniotwórczego za pomocą radiometru wyposażonego w sondę GM, pomiar przeprowadzono dla dwóch różnych grubości okienka
- wyznaczono charakterystykę kielichowego licznika GM, zmniejszając wartość napięcia mierzono liczbę zliczanych impulsów
- utworzono histogram źródła promieniotwórczego: liczebność serii pomiarowej - 1500, czas pojedynczego pomiaru - 0,1s.
4. Opracowanie wyników
Dla cienkiego okna radiometru zmierzono moc dawki badanej próbki na poziomie 100±10 [mGy/h], dal grubszego okienka moc dawki wyniosła 5±1 [mGy/h].
Stwierdzono obecność cząstek beta minus, ponieważ zmiana grubości okienka znacząco zmieniła ilość zarejestrowanych cząstek. Promieniowanie gamma jest zbyt przenikliwe, by zmiana była widoczna, natomiast cząstki alfa byłyby praktycznie całkowicie zatrzymane.
Reakcja rozpadu:
![]()
![]()
Charakterystyka licznika GM
U[V] |
I [imp/10s] |
780 |
2313 |
740 |
2268 |
700 |
2279 |
660 |
2267 |
620 |
2362 |
590 |
2208 |
560 |
2229 |
530 |
2147 |
500 |
2151 |
470 |
2004 |
460 |
1920 |
450 |
1988 |
440 |
1889 |
436 |
1888 |
432 |
1890 |
430 |
1731 |
428 |
1645 |
426 |
1204 |
424 |
762 |
422 |
309 |
420 |
0 |
Plateau:
Uprogowe = 420 [V]
U1 = 440 [V] I1 = 1889 [imp/10s]
U2 = 740 [V] I2 = 2268 [imp/10s]
Upracy = 600 [V]
Długość plateau:
U2-U1=740-440=300 [V]
Nachylenie Plateau:
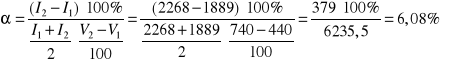
Badanie statystycznego rozpadu promieniotwórczego
Wybrano dwie zmienne losowe: k1=33 oraz k2=43 i policzono ich prawdopodobieństwo doświadczalne, poissonowskie i gaussowskie.
Parametry:
![]()
![]()
Dla k1=33
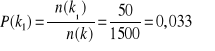
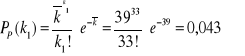
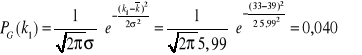
Dla k2=43
![]()
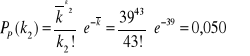
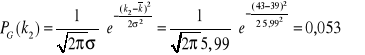
Rozkład Poissona - rozkład dyskretny, wykorzystywany do przedstawiania liczby wystąpień zjawiska w czasie dla określonej liczby prób. Rozkład jest określany na podstawie tylko jednego parametru (średnia). Nie jest symetryczny, a dla bardzo dużej liczby pomiarów można go przybliżać rozkładem Gaussa.
Rozkład Gaussa - podstawowy rozkład prawdopodobieństw dla zdarzeń przypadkowych. Jest to rozkład ciągły i symetryczny. Określany jest przez dwa parametry: średnią i odchylenie standardowe. Odchylenie standardowe jest miarą rozrzutu zmiennej losowej wokół wartości średniej. Rozkład Gaussa odgrywa ważną rolę w statystycznym opisie zagadnień przyrodniczych (np. rozkład natężenia światła), przemysłowych, medycznych czy socjologicznych. Stosowany jest przy opracowywaniu błędów pomiarowych.
Gdyby rozpad promieniotwórczy nie miał charakteru losowego histogram wyglądałby tak:
5. Wnioski
- Na podstawie wykonanych pomiarów udowodniono, że rozpad promieniotwórczy źródła promieniotwórczego ma charakter statystyczny i można go opisać za pomocą rozkładów Poissona oraz Gaussa
- Nachylenie plateau wyniosło kilka procent, a więc można założyć, że obliczenia były poprawne
- Udało się otrzymać dosyć podobne wartości prawdopodobieństwa doświadczalnego, Poissona i Gaussa, jednak prawdopodobieństwo doświadczalne wyraźnie odbiega od wartości Poissona i Gaussa, spowodowane jest to zbyt małą liczbą pomiarów
Wyszukiwarka
Podobne podstrony:
ĆWICZENIE 501, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Ćwiczenie 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i b
LABORATORIUM FIZYKI cw1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera
ĆWICZENIE 501LAST, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
Poprawa sprawozdania kwant gamma cw 15, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka l
Ćwiczenie 1 2, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Sprawozdanie nr 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
Sprawko - Licznik Geigera-Mullera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka liczni
LAB 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i badanie
LF 2 lab 4 +wiczenie 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-
1-licznik geigera-mullera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geige
Geigeiron, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i bad
Badanie charakterystyki licznika Geigera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka
+wiczenie1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i ba
Spraw1fizlab, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Lab.Fiz II-1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
sprawoad[1].betti, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
Rozkład doświadczalny 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera
więcej podobnych podstron