TEMAT ĆWICZENIA:
(1)
BADANIE CHARAKTERYSTYKI LICZNIKA GEIGERA-MÜLLERA
I STATYSTYCZNEGO CHARAKTERU ROZPADU PROMIENIOTWÓRCZEGO
WSTĘP
Celem ćwiczenia było zbadanie charakterystyki licznika Geigera-Müllera oraz statystycznego charakteru rozkładu promieniotwórczego.
Licznik Geigera-Müllera działa na zasadzie wyładowania lawinowego, powstającego wskutek wzmacniania procesów jonizacyjnych wywołanych promieniowaniem , promieniowaniem elektromagnetycznym γ lub rentgenowskim X. Jest on więc w stanie jedynie zarejestrować obecność promieniowania, nie zaś jego energię.
Badana w czasie wykonywana ćwiczenia próbka była źródłem promieniowania , którego rozkład można przedstawić następująco:
+
Na odcinku 90Sr - 90Y rozkład ma postać:
![]()
Zjawiska występujące w fizyce jądrowej mają charakter statystyczny - podczas pomiarów należy więc pamiętać, że oprócz niedokładności urządzeń pomiarowych trzeba także uwzględnić odchylenia spowodowane naturą zachodzących procesów, ich losowością.
Do opisywania prawdopodobieństwa otrzymania określonej liczby zliczeń (licznikiem Geigera-Müllera) stosuje się rozkład prawdopodobieństwa Poissona:
![]()
przy czym:
![]()
- wartość oczekiwana (średnia) zdarzenia rejestrowanego w stałym czasie t (liczba zliczeń, wokół której koncentrują się otrzymane wyniki).
Znajduje on zastosowanie w przypadku badania rozpadu promieniotwórczego, ponieważ prawdopodobieństwo rozpadu pojedynczego jądra jest bardzo małe oraz ilość jąder w źródle promieniotwórczym jest bardzo duża.
Gdy natomiast średnia liczba impulsów zliczanych przez licznik Geigera-Müllera jest duża, rozkład Poissona można przybliżyć rozkładem Gaussa:
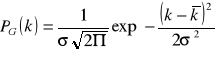
gdzie σ to odchylenie standardowe opisujące rozrzut rejestrowanych wartości impulsów.
UKŁAD POMIAROWY
Podczas wykonywania ćwiczenia wykorzystany został układ pomiarowy składający się z:
radiometru wyposażonego w sondę Geigera-Müllera oraz podłączonego do niego
zasilacza prądu zmiennego;
komputera z zainstalowanym programem Origin.
WYKONANIE ĆWICZENIA
Pomiar mocy dawki przy różnych grubościach okienka licznika Geigera-Müllera,
badanie charakterystyki licznika Geigera-Müllera:
wyznaczenie napięcia progowego (napięcie, poniżej którego wyładowanie lawinowe nie powstaje i promieniowanie nie może być zarejestrowane),
wyznaczenie obszaru plateau licznika,
określenie Upracy licznika;
badanie statystycznego charakteru rozpadu promieniotwórczego
wykonanie pomiarów przy użyciu programu CW1a,
eksport wyników do programu Origin oraz stworzenie wykresów;
opracowanie wyników.
WYNIKI I ICH OPRACOWANIE
Pierwszym pomiarem był pomiar mocy dawki pochłoniętej przy różnych grubościach okienka licznika Geigera-Müllera:
GRUBOŚĆ OKIENKA |
MOC DAWKI [Gy/h] |
ZAKRES LICZNIKA |
cienka |
90 |
300 |
gruba |
4 |
12 |
Na podstawie powyższych wyników stwierdzono, że obecne promieniowanie jest promieniowaniem , gdyż podczas pomiaru przy ustawionym grubym okienku pochłonięta została większość promieniowania - wyrzucony strumień elektronów został wyhamowany przez okienko licznika.
Następnie zbadano charakterystykę licznika Geigera-Müllera.
Po umieszczeniu próbki w domku pomiarowym napięcie progowe licznika wyznaczono stopniowo zmniejszając napięcie na zasilaczu oraz obserwując ilość zliczeń - gdy przestała się ona zmieniać, wartość napięcia została przyjęta za napięcie progowe licznika:
Uprogowe = 465 V
Kolejnym etapem badań było wyznaczenie obszaru plateau licznika. W tym celu, na zasilaczu ustawione zostało napięcie 700 V, które stopniowo było obniżane o 10 V, a następnie o 5V oraz 2 V (w miarę zbliżania się do wyznaczonej wcześniej wartości Uprogowe). Wyniki pomiarów przedstawia poniższa tabela (znajduje się ona także na stronie tytułowej sprawozdania):
U [V] |
700 |
690 |
680 |
670 |
660 |
650 |
640 |
630 |
620 |
610 |
600 |
590 |
N [imp] |
2442 |
2506 |
2486 |
2470 |
2431 |
2452 |
2240 |
2274 |
2346 |
2269 |
2269 |
2173 |
U [V] |
580 |
570 |
560 |
550 |
540 |
530 |
520 |
510 |
500 |
495 |
490 |
485 |
N [imp] |
2093 |
1991 |
1855 |
1855 |
1785 |
1792 |
1734 |
1710 |
1696 |
1640 |
1629 |
1382 |
U [V] |
480 |
478 |
476 |
474 |
472 |
470 |
468 |
466 |
464 |
462 |
460 |
|
N [imp] |
866 |
508 |
53 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Po przeniesieniu danych do programu Origin i stworzeniu wykresu, wygląda on następująco:
Na podstawie wykresu oraz tabeli wyników można określić napięcia U1 oraz U2. Wynoszą one:
U1 = 490 V,
U2 = 620 V.
Długość plateau wynosi zatem 130 V (różnica między U2 i U1).
Napięcie pracy licznika znajduje się pośrodku obszaru plateau (w połowie długości odcinka |U1,U2|)
i jest równe
![]()
Tak więc, w tym przypadku jest to
![]()
Kolejnym parametrem charakteryzującym licznik Geigera-Müllera jest nachylenie plateau, definiowane jako procentowy wzrost liczby impulsów przy zwiększeniu napięcia o 100 V (nie powinno ono przekraczać kilku procent). Wzór pozwalający obliczyć nachylenie plateau wygląda następująco:
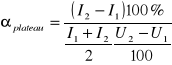
gdzie I1 oraz I2 to ilości impulsów odpowiadające napięciom U1 oraz U2.
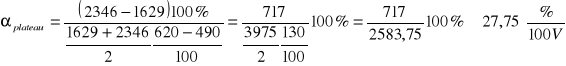
Metryka licznika wygląda zatem następująco:
Uprogowe = 465 V,
Upracy = 555 V,
długość plateau = 130 V,
plateau = 27,75 %/100V.
|
RACHUNEK BŁĘDÓW
![]()
![]()
![]()
![]()
![]()
0,001076 100 = 0,1076
plateau = 27,75 0,11 [%/100V]
BADANIE STATYSTYCZNEGO CHARAKTERU ROZPADU PROMIENIOTWÓRCZEGO
Preparat został poddany badaniom mającym ukazać statystyczny charakter jego rozpadu. W tym celu został on umieszczony w domku pomiarowym. Za pośrednictwem programu CW1a dokonano 2000 pomiarów co 0,1 sek.. Wartość oszacowanej średniej k wyniosła 20,35. Następnie, wyniki zostały wyeksportowane do programu Origin, po czym na ich podstawie stworzono histogram zależności impulsu o danej wartości od liczby jego wystąpień oraz dopasowanie Gaussa dla tych danych. Wydruk histogramu został załączony do sprawozdania. Zawiera on następujące wartości:
k = 21,
n(k) = 151,
kśr = 19,9
Następnie, określone zostanie prawdopodobieństwo doświadczalne dla wskazanej zmiennej losowej:
PRAWDOPODOBIEŃSTWO DOŚWIADCZALNE:
Wyraża się ono wzorem:
![]()
k = 22,
n(k) = 160,
n = 2000, a więc:
![]()
PRAWDOPODOBIEŃSTWO Z ROZKŁADU GAUSSA:
Z tabeli zamieszczonej obok histogramu możemy odczytać następujące wartości:
![]()
![]()
![]()
Wartość w równa jest:
![]()
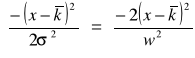
![]()
![]()
Prawdopodobieństwo znalezienia wskazanej liczby zliczeń (k = 22) dla rozkładu Gaussa wynosi:
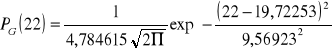
![]()
WNIOSKI
Podczas pracy z preparatami będącymi źródłem promieniowania należy stosować osłony
z materiałów o małej liczbie atomowej Z, co będzie skutkowało małym natężeniem rentgenowskiego promieniowania hamowania powstałym w czasie oddziaływania elektronów
z osłoną,
charakterystyka licznika Geigera-Müllera jest zbliżona do teoretycznej, jednak nachylenie plateau nie powinno przekraczać kilku procent - w czasie badań uzyskano wynik 27,75 0,11 [%/100V], co może świadczyć o niskiej klasie licznika lub jego zużyciu,
przeprowadzone badania potwierdziły statystyczny charakter rozpadu promieniotwórczego.
7
38
39
40
Z
90Y
90Sr
90Zr
Emax = 0,546 MeV
Emax = 2,27 MeV
![]()
![]()
T1/2 = 28 lat
T1/2 = 64 h
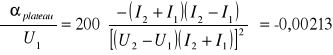
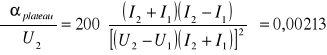
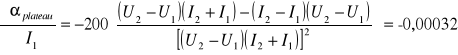
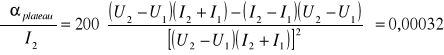
Wyszukiwarka
Podobne podstrony:
ĆWICZENIE 501, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Ćwiczenie 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i b
LABORATORIUM FIZYKI cw1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera
ĆWICZENIE 501LAST, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
fiza2, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i badanie
Poprawa sprawozdania kwant gamma cw 15, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka l
Ćwiczenie 1 2, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Sprawozdanie nr 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
Sprawko - Licznik Geigera-Mullera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka liczni
LAB 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i badanie
LF 2 lab 4 +wiczenie 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-
Geigeiron, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i bad
Badanie charakterystyki licznika Geigera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka
+wiczenie1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i ba
Spraw1fizlab, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Lab.Fiz II-1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
sprawoad[1].betti, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
Rozkład doświadczalny 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera
więcej podobnych podstron