Wstęp teoretyczny
Rozpad promieniotwórczy jest zjawiskiem spontanicznym, w wyniku którego zmienia się bądź skład nukleonowy jądra atomowego ulegającego rozpadowi, bądź też zmienia się stan energetyczny tego jądra. Podstawowe prawa rozpadu promieniotwórczego zostały odkryte i opracowane przez A.H.Becquerela i zbadane przez M.Skłodowską-Curie i P.Curie. Są to przemiany: (alfa), (beta), γ (gamma). Wszystkie przemiany podlegają temu samemu prawu rozpadu spontanicznego: (-t). Stała rozpadu związana jest z okresem połowicznego zaniku . Prawo to określa liczbę jąder w próbce promieniotwórczej tylko statystycznie, tj. z dokładnością do fluktuacji statystycznych.
W warunkach laboratorium studenckiego, ze względu na bardzo długi czas połowicznego zaniku próbki promieniotwórczych nie jesteśmy w stanie udowodnić wykładniczego malenia aktywności próbki. W czasie badania tej aktywności w naszych warunkach jesteśmy w stanie zbadać jedynie niewielki wycinek krzywej, który można uznać za linię prostą o zerowym nachyleniu. Dlatego celem ćwiczenia jest zbadanie stochastycznego (przypadkowego) charakteru rozpadu promieniotwórczego. Dowodem na to jest istnienie pewnych fluktuacji statystycznych (odchyleń), wokół pewnej wartości średniej.
Tak więc, jeżeli rozpad promieniotwórczy jest procesem przypadkowym, należy oczekiwać, że dla jąder o odpowiednio długim okresie połowicznego zaniku, rozkład prawdopodobieństwa rejestracji danej liczby rozpadów w stałym okresie czasu będzie zgodny z teoretycznym rozkładem prawdopodobieństwa zdarzeń przypadkowych.
Przebieg ćwiczenia
Celem ćwiczenia jest zapoznanie się z budową i zasadą działania licznika Geigera-Mullera oraz poznanie statystycznych praw opisujących rozpad promieniotwórczy.
Wyznaczenie charakterystyki roboczej licznika Geigera-Mullera
W pierwszej części ćwiczenia wyznaczaliśmy charakterystykę roboczą licznika
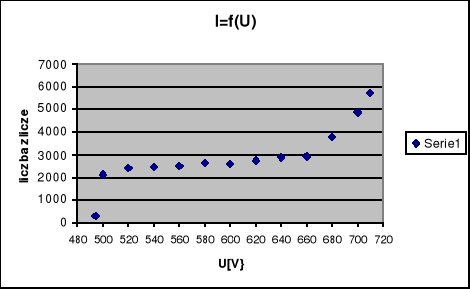
I=f(U), gdzie
I - liczba zliczonych impulsów w danym czasie
U - napięcie pomiędzy katodą a anodą licznika
U[V] |
494 |
500 |
520 |
540 |
560 |
580 |
600 |
620 |
640 |
660 |
680 |
700 |
710 |
liczba zliczeń |
302 |
2128 |
2389 |
2480 |
2528 |
2656 |
2609 |
2740 |
2865 |
2949 |
3803 |
4864 |
5739 |
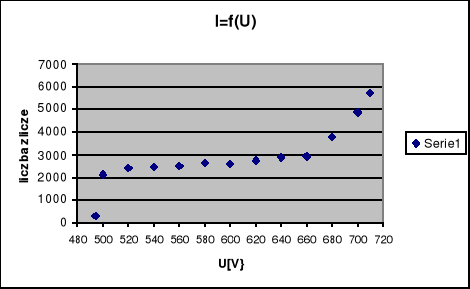
Bazując na otrzymanym wykresie można określić napięcie progowe Vgr=494[V} oraz obszar `plateau' zawarty pomiędzy wartościami:
U1=540[V]
U2=660[V]
Zatem napięcie pracy wynosi:
Up=0.5*(U1+U2)
Up=600[V]
Długość obszaru `plateau' wynosi:
U12=U2-U1
U12=120[V]
Nachylenie `plateau' wynosi:
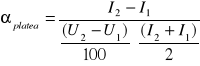
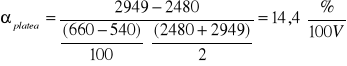
Rachunek błędów
Błąd wyliczenia zarejestrowanych impulsów wynika głównie ze statystycznego rozkładu promieniowania, co powoduje rozrzut punktów pomiarowych względem odcinka prostego `plateau' oraz z tego iż różny odsetek impulsów docierających do licznika zostaje zarejestrowany. Błąd pomiaru czasu można w porównaniu z powyższymi błędami uznać za nie istotny. Zakładam więc graniczny błąd zliczania impulsów równy ΔI=2%.
Stąd ΔI1=ΔI*I1=49.6[impulsów/min]
ΔI2=ΔI*I2=59[impulsów/min]
Zakładam, że graniczny błąd nastawienia napięcia licznika jest równy wartości działki elementarnej pokrętła.
ΔU=ΔU1=ΔU2=2[V]
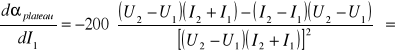
Korzystając z metody różniczki zupełnej:
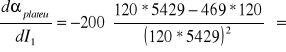
![]()
![]()
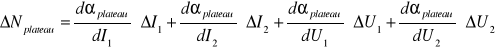
2.8*10-4
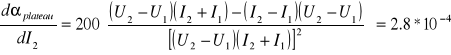
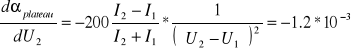
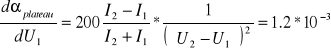
![]()
![]()
%=4,7%/100V
Nplateau=[14,4+-4,7]%/100V
Wnioski:
Wyznaczona charakterystyka ma kształt, który był oczekiwany. Fragment szybkiego wzrostu I(szybkości zliczania impulsów) po przekroczeniu napięcia progowego jest bardzo stromy. Świadczy to o tym, że licznik jest prawie tak samo wrażliwy na większość cząstek do niego docierających. Wynika to z tego, że impulsy wywołane przez dużą część wyzwalających licznik cząstek ma bardzo zbliżoną amplitudę. Obszar plateau charakteryzuje się dość dużym pochyleniem(rzędu 15%), co świadczy o niezbyt wysokiej klasie badanego licznika. Potwierdza to również długość obszaru plateau, która nie jest zbyt duża. Na końcu obszaru plateau charakterystyka rośnie łagodnie parabolicznie, co spowodowane jest wzrostem prawdopodobieństwa wyładowania samoistnego. Wyładowanie takie powoduje zliczenie `fałszywego' impulsu ,który nie jest wywołany przez cząstkę wyemitowaną z badanej próbki promieniotwórczej. Napięcia progowe i napięcia pracy są wysokie, co może sugerować, że badany licznik nie jest licznikiem o obniżonym napięciu pracy. Jego charakterystyka robocza zgadza się z opisem licznika wypełnionego argonem z parami alkoholu w roli gazu gaszącego. Zmierzone promieniowanie tła, które wynosiło Itła=55 imp./min, jest nieznaczne w porównaniu do promieniowania badanego preparatu promieniotwórczego i w znikomy sposób mogło wpłynąć na uzyskane wyniki.
Czas martwy licznika Geigera-Mullera
Nr preparatu |
t[min] |
N[imp] |
In[imp/min] |
I=In-Itła[imp/min] |
1 |
10 |
153734 |
15374 |
15358 |
1+2 |
10 |
300232 |
30230 |
30214 |
2 |
10 |
164122 |
16412 |
16396 |
Korzystając z przybliżonej wartości na czas martwy licznika można określić jego wartość. Zależność ta została wyprowadzona w oparciu o równanie, które stwierdza równość między rzeczywistą aktywnością obu próbek jednocześnie i sumą rzeczywistych aktywności każdej próbek z osobna. Wyniki pomiarów aktywności za pomocą licznika Geigera-Mullera stwierdzają brak takiej zgodności w przypadku aktywności zmierzonych. Wynika ona z tego, że pomiar aktywności obarczony jest błędem wynikającym z istnienia czasu martwego. Czas martwy powoduje, że przy pomiarze większych aktywności pominięta zostanie większa liczba cząstek, które powinny wzbudzić licznik i wywołać zliczenie kolejnego impulsu, niż przy pomiarze mniejszych aktywności. Spowodowane jest to tym, że cząstki są częściej wysyłane i częściej trafiają na licznik w stanie martwym. Dlatego zmierzona aktywność połączonych próbek jest mniejsza niż suma zmierzonych aktywności obu próbek z osobna. Znając zależność między intensywnością rzeczywistą a intensywnością zmierzoną i czasem martwym licznika można dojść do zależności:
![]()
![]()
-czas martwy licznika;
I1-zmierzona intensywność pierwszej próbki;
I2-zmierzona intensywność drugiej próbki;
I1,2-zmierzona intensywność obu próbek;
![]()
=5,25![]()
Analiza błędów
Na błąd wyznaczenia zmierzonej aktywności próbki wpływają następujące czynniki:
-statystyczny charakter rozpadu promieniotwórczego. Powoduje on uzyskanie wartości
wartości zliczonych impulsów dla tej samej próbki i tego samego czasu zliczania
różniących się między sobą w sposób losowy. W celu zmniejszenia tego błędu wydłużono czas pomiaru do 10 min. Zakładam że błąd ten jest z rzędu 0.1%
![]()
![]()
![]()
-błąd wynikający z tego, że przy pomiarze aktywności obu preparatów promieniotwórczych jednocześnie znajdowały się one w innym położeniu względem licznika niż przy pomiarze aktywności każdego preparatu z osobna. W rzeczywistości były one rozsunięte względem pozycji, w której największa cześć promieniowania wysyłanego przez próbkę dociera do aktywnej części licznika. Dlatego wynik pomiaru dla obu próbek jednocześnie jest zaniżony
względem wartości, którą uzyskalibyśmy, gdyby obie próbki można było zespolić i umieścić dokładnie pod licznikiem. Zakładam, że błąd wyznaczenia aktywności wynosi:
![]()
![]()
Podsumowując można wyznaczyć wartości błędów zmierzonych aktywności:
![]()
![]()
![]()
Korzystając z metody różniczki zupełnej można wyznaczyć błąd wartości czasu martwego:
![]()
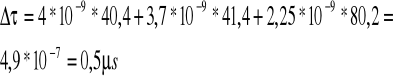
Wynik pomiaru czasu martwego licznika wynosi:
![]()
Wnioski:
Uzyskana wartość czasu martwego licznika jest dość znaczna jak na aktywność preparatów promieniotwórczych stosowanych podczas ćwiczenia. Widać to bezpośrednio na różnicy między sumą aktywności dwóch próbek i aktywności tych próbek razem, która osiąga ok.8%. Świadczy to o konieczności uwzględnienia czasu martwego przy pomiarach próbek o dużej aktywności. Uzyskana wartość ![]()
jest względnie duża, jednak jej zmniejszenie w większości przypadków zastosowań licznika Geigera-Mullera nie ma sensu. Powodowałoby to ono konieczność stosowania urządzeń droższych, których konstrukcja i gaz wypełniający pozwalają zmniejszyć czas martwy.
Zmniejszenie ![]()
kosztem wzrostu ceny licznika mija się z celem, gdyż najczęściej pracuje on jako wskaźnik napromieniowania substancji, mierzący stopień napromieniowania. Zatem zwiększenie dokładności pomiaru aktywności nie jest tu konieczne. Czas martwy wyznaczony został z dość dużym błędem granicznym, który prawdopodobnie powinien być większy ze względu ze względu na źródła błędów, które nie zostały ustalone. Uzyskana wartość nie budzi jednak żadnych zastrzeżeń z mojej strony i mogę ją przyjąć jako poprawną.
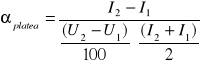
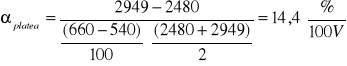
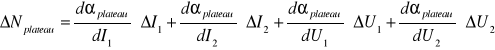
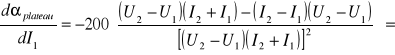
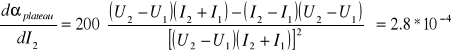
![]()
![]()
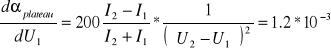
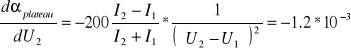
Wyszukiwarka
Podobne podstrony:
ĆWICZENIE 501, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Ćwiczenie 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i b
LABORATORIUM FIZYKI cw1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera
ĆWICZENIE 501LAST, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
fiza2, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i badanie
Poprawa sprawozdania kwant gamma cw 15, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka l
Ćwiczenie 1 2, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Sprawozdanie nr 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
Sprawko - Licznik Geigera-Mullera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka liczni
LAB 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i badanie
LF 2 lab 4 +wiczenie 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-
1-licznik geigera-mullera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geige
Badanie charakterystyki licznika Geigera, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka
+wiczenie1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i ba
Spraw1fizlab, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Lab.Fiz II-1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
sprawoad[1].betti, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
Rozkład doświadczalny 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera
więcej podobnych podstron