1. Ruch po okręgu

Ruch po okręgu jest szczególnym przypadkiem ruchu krzywoliniowego płaskiego, jego najprostszym przykładem. W ogólnym przypadku ruch ten opisujemy równaniami postaci:

x= x₀+ r cos ϕ (t)

y= y₀+ r sin ϕ (t)

Gdy dowolny punkt porusza się po obwodzie koła, to promień łączący go ze środkiem koła, czyli jego promień wodzący r, zakreśla kąt, który rośnie w miarę upływu czasu, czyli kąt ϕ jest funkcją czasu.

Jest to ruch po okręgu o środku w punkcie (x_0, y₀) i promieniu r. Jeżeli początkiem układu odniesienia O jest środek okręgu równania mają postać:

x= r cos ϕ (t)

y= r sin ϕ (t)

Kąt φ - droga kątowa

Drogę liniową przebytą przez ciało po łuku koła, za pomocą drogi kątowej wyraża

s= φr

Prędkość kątowa

=
ϕ=
t [rad/s] dla ruchu jednostajnego:
=
=const.

Jeżeli prędkość kątowa w tym ruchu jest const --> ruch jednostajny po okręgu

0

Gdy ruch jest niejednostajny --> wprowadza się przyspieszenie kątowe

Przyspieszenie kątowe
[rad/s²];

ruch w którym przyspieszenie jest stałe i różne od 0 --> jednostajnie zmiennym po okręgu.

Chwilową prędkość kątową określamy w sposób następujący :

ω=lim(dt -> 0) dϕ/dt.

prędkość liniowa punktu przyjmuje wartość V=ωr lub V=ω ^X r

V=ωrsinϕ

Wektor przyspieszenia jest sumą wektora dośrodkowego przysp. i wektora przysp. stycznego.

a=(α/ω)v-ω²r ; a_s + a_d =a

przysp. dośrodkowe (przyśpieszenie normalne)- a_n=-ω²r (skierowane do środka koła , przeciwnie do r).

A więc i przyśpieszenie chwilowe będzie skierowane ku środkowi, dlatego nazywamy je przyśpieszeniem dośrodkowym. Gdy punkt przebywa cały okręg koła ruchem jednostajnym w czasie T zwanym okresem,

Ruch jednostajny po okręgu jest ruchem periodycznym o okresie T =

częstotliwość

to jego promień wodzący opisuje kąt 2π, zatem ω=2π/T a(n)=4π²r/T²,

Przyspieszenie normalne

a_n=

a_n=
= const.

Przyspieszenie styczne a_s=
a_s= 0

2. Układy inercjalne i nieinercjalne

UKŁAD INERCJALNY - układ w którym ciało, na które nie działają żadne siły lub działające siły się równoważą, pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. Układ odniesienia w którym obowiązuje i spełniona jest zasada bezwładności, czyli I zasada dynamiki. W układach tych obowiązują również pozostałe zasady dynamiki.

Układ odniesienia związany z Ziemią

UKŁAD NIEINERCJALNY - porusza się ruchem jednostajnie przyspieszonym względem inercjalnego, obraca się ruchem jednostajnym względem inercjalnego. W układzie tym trzeba wprowadzić pewne siły pozorne nazywane siłami bezwładności, zależne jedynie od wyboru układu odniesienia:

Siła odśrodkowa bezwładności F_ob = m
²r

Siła Coriolisa bezwładności F_ob = -2m
^x V

Przykładem może być opis zachowania kulki z pkt widzenia obserwatora w układzie inercjalnym i w układzie nieinercjalnym wagonika.

ruszający z miejsca wagon kolejowy

Startująca rakieta dla kosmonauty

Człowiek w windzie

3. Pęd. Zasada zachowania pędu

Pęd: wektorowa wielkość fizyczna charakteryzująca ruch obiektu , równa dla punktu materialnego iloczynowi jego masy i prędkości

p=m*v

(wektor skierowany zgodnie ze zwrotem prędkości)

Jednostką pędu jest 1 kg*m / s

W oparciu o pęd można sformułować II zasadę dynamiki Newtona

F=dp/dt

(siła działająca na ciało jest równa pochodnej pędu względem czasu)

Fdt=dp → (popęd działania siły jest równy przyrostowi pędu)

Zasada zachowania pędu: Jeżeli wypadkowa sił zewnętrznych F_Z=0 to p=const

Jeśli wypadkowa sił wewnętrznych Fw=0 to suma pędów układu = pędowi całkowitemu

Prawo zachowania pędu: Jeżeli na ciało lub układ ciał nie działają siły zewn.

(układ izolowany) to pęd układu jest stały przed i po zjawisku (wektor tego pędu układu jest stały). Zasada ta wynika z II zas dynamiki.

Pęd punktu materialnego jest różny w różnych inercjalnych układach odniesienia, ale zasada zachowania pędu obowiązuje w każdym inercjalnym układzie

4. Moment pędu. Moment siły dla punktu materialnego

Moment pędu punktu materialnego jest to wektor prostopadły do promienia wodzącego r i pędu p=mV punktu w danej chwili czasu

L= r^xp (iloczyn wektorów r i p)

Długość wektora L jest równa z definicji polu równoległoboku zbudowanego na wektorach r i p. Zwrot wektora L określa reguła śruby prawoskrętnej: przy obrocie śruby od r do p o kat mniejszy od półpełnego kierunek przesuwu śruby wskazuje zwrot wektora L. Jeżeli wektory r i p leżą w stałej płaszczyźnie, to wektor L jest stale prostopadły do tej płaszczyzny.

Z definicji momentu pędu wynika, że jest to wielkość zależna od wyboru układu odniesienia, różna nawet w różnych układach odniesienia.

Moment siły jest również wielkością wektorową. Z definicji jest to wektor prostopadły do płaszczyzny wyznaczonej przez wektory r i F przechodzący przez pkt 0.

M= r^xF

Wartość momentu określa równanie M= rFsin(r,F)= rFsin
= F(rsin
)= Fd

Zwrot znajduje się z ruchu postępowego śruby prawoskrętnej jeżeli pierwszy czynnik iloczynu r obraca się do pokrycia z wektorem F.

5. Siły zachowawcze i niezachowawcze

Siła jest to fizyczna wielkość wektorowa, którą mierzymy za pomocą dynamometru, jest ona miarą oddziaływań, które mogą powodować przyspieszenia ciał w układzie inercjalnym i odkształcenia ciał

Siły zachowawcze: przykładem jest siła sprężysta, siła pola grawitacyjnego

Siły niezachowawcze: terminem tym obejmujemy tarcie i inne siły zewnętrzne , dla których nie można wprowadzić pojęcia energii potencjalnej

Praca sił niezachowawczych = zmianie całkowitej energii mechanicznej pkt materialnego podczas ruchu

6. Układ punktów materialnych. Środek masy. Ruch środka masy

Układ punktów materialnych to układ co najmniej dwóch ciał traktowanych jako punkty materialne o masach m_i. Położenia tych punktów określone są w wybranym układzie współrzędnych przez wektory r_i.

Środek masy jest to punkt, którego wektor położenia r_s określony jest wzorem:

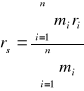
dla rozkładu dyskretnego mas

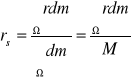
dla rozkładu ciągłego mas

jeżeli masy są sobie równe , to środek masy leży zawsze w połowie odległości między tymi punktami materialnymi. W ogólnym przypadku leży on zawsze na prostej łączącej oba punkty, bliżej tego punktu który ma większą masę.

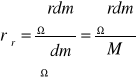
Ruch środka masy środek masy układu punktów materialnych porusza się tak, jak poruszałby się punkt materialny o masie równej całkowitej masie układu pod działaniem siły równej sumie wszystkich sił zewnętrznych, działających na poszczególne punkty układu. Środek porusza się zatem zgodnie z II zasadą dynamiki Newtona

7. Ruch postępowy i obrotowy bryły sztywnej

W zależności od tego, jakim ruchem względem układu odniesienia porusza się układ związany z bryłą, ruchy bryły dzielimy na postępowe, obrotowe i złożone.

Ruch postępowy: w ruchu tym wszystkie punkty bryły poruszają się po identycznych krzywych przesuniętych równolegle względem siebie. W tym przypadku do pełnego opisu ruchu bryły wystarcza opis dowolnego jej punktu Ruch obrotowy: istnieje wiele rodzajów ruchów obrotowych, jednym z nich jest ruch wokół ustalonej osi.

Ruchem obrotowym porusza się bryła której dwa dowolne punkty O i O' zostały unieruchomione względem układu odniesienia. Prosta O'O stanowi oś obrotu bryły.

Opis ruchu bryły sztywnej wokół ustalonej osi polega na określeniu zależności kąta  od czasu

  (

prędkość kątową bryły  definiujemy wartością


znak prędkości kątowej również zależy od kierunku obrotu bryły. Przyspieszenie kątowe bryły

 =
=

Ze względu na stałość odległości między punktami bryły wielkości  ,,  charakteryzują jednocześnie ruchy wszystkich punktów bryły sztywnej po okręgach, z wyjątkiem pkt położonych na osi obrotu.

Wielkości prędkości Vs oraz przyspieszenie styczne as są różne dla różnych pkt, można je wyrazić

gdzie l jest odległością pkt od osi obrotu

wyróżniamy ruch jednostajny

jednostajnie zmienny

niejednostajny opisany wyżej

8. Moment bezwładności bryły sztywnej

występującą wzorze na energię kinetyczną sumę nazywamy momentem bezwładności ciała względem danej osi obrotu z i oznaczamy symbolem I_z [kg*m²]

wielkość momentu bezwładności w istotny sposób zależy od tego, wokół jakiej osi obraca się bryła. Ważną cecha momentu bezwładności jest addytywność- moment bezwładności łożony z kilku części równy jest sumie momentów bezwładności poszczególnych części bryły względem tej samej osi obrotu.

Cienki pręt I₀₀=ml²/12

Cienka tarcza I₀=mr²/2

Cienka obręcz I₀=mr²

Walec-I₀₀=mr²/2

KulaI₀₀=²/₅mr²

9. Energia kinetyczna i moment pędu bryły sztywnej

Energia kinetyczna Traktując bryłę sztywną jako układ n punktów materialnych obliczamy energię kinetyczną bryły obracającej się wokół ustalonej osi, masę poszczególnych pkt materialnych oznaczamy przez m_i a ich prędkości przez V_i ,całkowita energia kinetyczna bryły

Ekin=

W ruchu postępowym prędkości wszystkich pkt bryły są równe, a więc w ruchu postępowym

E_kin=

Gdzie M=
jest masą bryły

W ruchu obrotowym wokół ustalonej osi prędkości Vs różnych pkt są różne można je jednak powiązać z prędkością kątową bryły

V_is=

Gdzie l_i jest odległością i-tego pkt od osi obrotu.

Energię kinetyczną ruchu wokół ustalonej osi obrotu można więc przedstawić w postaci

gdzie
= I_z

prawo Steinera I=Iśr + Md²

M masa bryły

d odległość od osi obrotu przechodzącej przez środek bryły i normalną osi

moment pędu moment pędu bryły sztywnej oznacza się literą L i jest to wektor równy sumie wektorów momentów pędu poszczególnych pkt materialnych składających się na bryłę (może być wielkością dodatnią lub ujemną w zależności od kierunku obrotu bryły )

L=

Jednostka [kg*m²/s]

Wektor prostopadły do wektora pędu p i wektora wodzącego pkt materialnego r wartość równa iloczynowi promienia okręgu i wartości wektora pędu zwrot zależy od kierunku obiegu pkt po okręgu.

Moment pędu można również wyrazić poprzez moment bezwładności i prędkość kątową

10. Zjawisko rezonansu dla drgań harmonicznych

Drgania jakiejkolwiek wielkości fizycznej x nazywamy harmonicznymi jeżeli ich zależność od czasu t ma postać:

x = A⋅sin (ωt + ϕ₀) lub x = A⋅cos (ωt + ϕ₁)

jeżeli częstotliwość padającej na ciało fali harmonicznej jest równa częstotliwości drgań własnych ciała, nawet fala o niewielkiej amplitudzie może wzbudzić silne drgania ciała, mówi się wówczas że ciało drgające znajduje się w rezonansie z innym ciałem drgającym, które stanowi źródło fali padającej. Ciało pobudzone do drgań samo staje się źródłem fali rozchodzącej się w otaczającym ośrodku. Amplituda drgań ciała wzrasta dopóty, dopóki energia wysyłanej przez to ciało fali nie zrówna się z energią fali pochłanianej.

11. Podstawowe prawa statyki cieczy

W zakresie ciśnień bliskich atmosferycznemu, gęstość cieczy uznajemy za stałą to założenie, w połączeniu z prawem Pascala, stanowi podstawę statyki cieczy. Z prawa Pascala wynika że parcie cieczy może zrównoważyć tylko takie siły zewnętrzne które działają prostopadle do powierzchni cieczy, jeżeli wypadkowa siła zewnętrzna ma składową styczną do powierzchni cieczy, to ciecz musi zmienić swój kształt. Ciecz znajduje się w stanie równowagi gdy

1. siły zewnętrzne działające na pow ograniczającą są w każdym pkt prostopadłe do powierzchni

2. siła zewnętrzna przypadająca na każdy element s pow cieczy jest zrównoważona przez siłę parcia cieczy na ten element pow

p=p0+hdg p₀ ciśnienie w dowolnym pkt cieczy

W cieczach obowiązuje również prawo wyporu Archimedesa (W jednorodnym polu grawitacyjnym o natężeniu g na ciało zanurzone w cieczy działa siła wyporu F_w skierowana przeciwnie do kierunku pola, jej wartość równa jest ciężarowi cieczy wypartej przez ciało)

F_w= - Vdg

dg = D -ciężar właściwy

F_w = -VD

12. Przepływ cieczy nieściśliwej

Badaniem zjawiska ruchu cieczy zajmuje się nauka zwana hydrodynamiką. Najprostszym ruchem cieczy jest przepływ stacjonarny idealnej cieczy nieściśliwej. PRZEPŁYW STACJONARNY jest to przepływ w którym prędkość cieczy przepływającej przez każdy ustalony pkt przestrzeni jest stała w czasie, np. przepływ wody w przewodach wodociągowych. CIECZ IDEALNA to ciecz w której ruch jednych warstw cieczy względem innych zachodzi bez tarcia, ciecz w której siły tarcia są mniejsze od sił ciężkości, ciśnienia zewnętrznego. CIECZ NIEŚCIŚLIWA ciecz której gęstość jest stała niezależna od ciśnienia ani innych sił zewnętrznych. Przy przepływie stacjonarnym idealnej cieczy nieściśliwej wzdłuż lini prądu cieczy rządzi prawo Bernoulliego, spełniona jest równość:

p + dV²/2 + dgz = const.

p ciśnienie w danym pkt

d gęstość

V prędkość

g przyspieszenie ziemskie

z wysokość względem dowolnie wybranego poziomu zerowego

LINIA PRĄDU linia w każdym swoim pkt styczna do wektora prędkości cieczy w danym pkt, linia prądu pokrywa się z torem ruchu wybranej cząsteczki cieczy

13. Zastosowanie równań przepływu cieczy dla opisu przepływu w gazach

Pojęcie cieczy nieściśliwej ma pewne zastosowanie przy badaniu przepływu gazów. Dzięki małej gęstości, do wprawiania gazu w ruch wystarczy bardzo mała zmiana ciśnienia. Aby nadać strumieniowi powietrza prędkość 10 m/s, wystarczy dodatkowe ciśnienie rzędu jednej tysięcznej ciśnienia atmosferycznego. Przy tak niewielkich zmianach ciśnienia zmiany gęstości gazu można zaniedbać. Prawo Bernoulliego sformułowane dla cieczy pozwala wyjaśnić zasadę lotu samolotu. Dzięki odpowiedniemu kształtowi skrzydła w stanie stacjonarnym prędkość względnego ruchu cząstek powietrza jest tuż ponad skrzydłem większa, a tuż pod nim mniejsza niż prędkość względnego ruchu cząstek w oddaleniu od skrzydła. Korzystając z prawa Bernoulliego łatwo wykazać że na dolną pow skrzydła działa ciśnienie większe, a na górną mniejsze od atmosferycznego. W związku z tym na skrzydło działa wypadkowa siła F skierowana ku górze, zwana siłą nośną. Aby samolot módl się oderwać od ziemi siła nośna musi być większa od ciężaru samolotu w powietrzu dlatego samolot musi się najpierw rozpędzić. Ciężar samolotu w powietrzu to ciężar zmniejszony o siłę wyporu

14. Fale. Równanie falowe

Fala - zaburzenie stanu ośrodka lub pola elektromagnetycznego, rozchodzące się w przestrzeni ze skończoną prędkością i niosące ze sobą en (fale umożliwiają przepływ en na duże odległości), przepływowi en nie towarzyszy przepływ masy, np. światło, dźwięk.

elektromagnetyczne- zaburzenia stanu pola elektr. Rozchodzące się w przestrzeni, w próżni i ośrodkach materialnychświatło

fale długie, średnie, krótkie, ultrakrótkie

sprężyste- zaburzenia stanu ośrodków materialnych, w gazach zaburzenia gęstości, cieczach zaburzenia gęstości kształtu pow swobodnej, ciałach stałych zaburzenia gęstości lub kształtu(regularności sieci krystalicznej)dźwięk

Periodyczne (harmoniczne), nieperiodyczne

Podłużne, poprzeczne

kuliste (promienie fali układają się radialnie, powierzchnie falowe tworzą wycinki sferyczne),

walcowe,

płaskie jeżeli zaburzenie rozchodzi się w jednym kierunku fala jest nazywana płaską (powierzchnie falowe są płaszczyznami, a promienie fali liniami prostymi równoległymi do siebie)

akustyczne

Impulsowe

Fale mogą być jedno-, dwu-, trójwymiarowe.

Równanie falowe:

15. Fale podłużne, poprzeczne, fale na powierzchni cieczy

Jeżeli ruchy cząstek materii przenoszącej falę są prostopadłe do kierunku rozchodzenia się fali, wówczas mamy do czynienia z falą poprzeczną np. zaburzenie porusza się wzdłuż liny (rozchodzą się w ciałach stałych)

Jeżeli cząsteczki przenoszące falę mechaniczną poruszają się do przodu i do tyłu wzdłuż kierunku rozchodzenia się fali, wówczas mamy do czynienia z falą podłużną np. naprzemiennie rozciągana i ściskana sprężyna pionowa (rozchodzą się w cieczach i gazach, ciałach stałych)

Fale mogą być mieszane tj. poprzeczne i podłużne np. fale wody. Po swobodnej pow cieczy mogą rozchodzić się fale, które sprawiają wrażenie fal poprzecznych. Poprzeczne wychylenie w warstwie powierzchniowej prowadzi do zwiększenia pow swobodnej. Przeciwdziałają temu siły napięcia pow. W rzeczywistości w ruchu falowym pow cieczy biorą udział głębsze warstwy cieczy, toteż przebieg zjawisk jest bardziej skomplikowany. Cząstki cieczy poruszają się po torach kołowych i eliptycznych w płaszczyznach równoległych do kierunku rozchodzenia się fali. Fala na pow cieczy nie jest więc ani falą podłużną ani poprzeczną

16. Interferencja fal. Fale stojące

Interferencja zjawisko nakładania się na siebie dwóch lub więcej fal harmonicznych o tej samej długości, prowadzącej do powstania ustalonego w czasie rozkładu przestrzennego obszarów wzmocnienia i osłabienia fali.

Fala stojąca fala o jednakowych amplitudach a i o częstotliwościach , ale rozchodzących się w przeciwnych kierunkach.

Wynikiem interferencji jest to ze każdy punkt na osi x drga ruchem harmonicznym z częstotliwością , ale amplitudy drgań różnych punktów są różne. Tego rodzaju obraz interferencyjny nosi nazwę fali stojącej. Punkty w których amplituda drgań równa jest 0 noszą nazwę węzłów fali stojącej, odległość między sąsiednimi węzłami jest równa połowie długości fali. Fala stojąca zawdzięcza swoją nazwę temu, ze węzły i strzałki fali zajmują stałe położenie, niezależne od czasu.

17. Fale akustyczne. Efekt Dopplera

Fala akustyczna (dźwiękowa):

Falą akustyczną nazywamy podłużną falę zagęszczeń i rozrzedzeń ośrodka, mogące rozchodzić się w ciałach stałych, ciekłych i gazach. Fale dźwiękowe obejmują pasmo częstotliwości od ok.16 do 20 000 Hz. Fale o częstotliwościach drgań niższych niż 16 Hz nazywane są infradźwiękami, wyższe niż 20 000 Hz nazywane są ultradźwiękami.

Cechy dźwięku:

-wysokość - zależy od częstotliwości drgań źródła

-barwa (brzmienie) - cecha charakterystyczna danego źródła dźwięku pozwalająca określić co wydaje dźwięk

-głośność (siła brzmienia) - wrażenie słuchowe uzależnione również od częstotliwości dźwięku

Zjawisko Dopplera polega na pozornej zmianie wysokości dźwięku, wywołanego przez źródło, w wyniku względnego ruchu obserwatora i źródła.

' = 

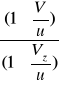
gdzie

u to prędkość fali,

 to częstotliwość źródła,

' to rejestrowanie

Obserwator zbliżający się do źródła słyszy dźwięk o częstotliwości wyższej od częstotliwości własnej źródła, natomiast obserwator oddalający się od źródła słyszy dźwięk o częstotliwości niższej od częstotliwości własnej źródła

18. OPORNOŚĆ FALOWA OŚRODKA

in. impedancja falowa, Z , wielkość charakteryzująca reakcję ośrodka na zaburzenie wywołane rozchodzącą się w nim falą. Jednostką jest [om].

Z= p _max/V _o Z=  u

V _o maksymalna prędkość cząsteczek

 gęstość ośrodka

u prędkość rozchodzenia się fali w ośrodku

Z₁<Z₂ ośrodek Z₁ rzadszy od ośrodka Z₂

 

Z₁>Z₂  

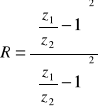
odbicie Z₁=Z₂R= 0

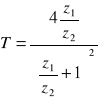
przejście

19. Rozkład Boltzmana dla gazu doskonałego

Statystyczne prawo rozkładu prędkości cząsteczek gazu doskonałego, poruszających się w polu sił: Rozkład Boltzmana pozwala określić prawdopodobieństwo posiadania przez cząstkę Ep

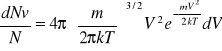
f(V)

prawdopodobieństwo znalezienia w gazie cząstki o pr. V

Prawo to pozwala wyznaczyć wzór określający zmniejszanie się liczby cząsteczek wraz ze wzrostem wysokości w polu sił ciężkości, służy do wyznaczania stałej Avogadra.

20. Rozkład Maxwella dla gazu doskonałego

Statyczne prawo rozkładu prędkości ruchu postępowego cząsteczek gazu doskonałego przy ustalonej temperaturze.

V _śr= ok. 10⁴-10^{5 cm} /_s T=300K

Warunek cząstki nie mogą się zderzać

Jedno z podstawowych praw kinetycznej teorii gazów. Zgodnie z prawem rozkładu Maxwella na wykresie przedstawiającym zależność

n / n od u (n całkowita ilość cząstek,  n ilość cząstek, których prędkości są zawarte między u i u + u), maksimum krzywej wyznacza prędkość najbardziej prawdopodobną u_p. Wartość u_p w danej temp jest tym większa im mniejsze są masy cząsteczek.

Prawo to nie uwzględnia oddziaływań między cząsteczkami , sił zewnętrznych, ani ruchu wewnątrzcząsteczkowego.

21. Transport pędu i energii- opis mikroskopowy

Transport pędu Zmiana pędu następuje na skutek przejścia cząstek z jednej warstwy do drugiej. Z transportem pędu bezpośrednio wiąże się zjawisko lepkości, o którego istnieniu świadczy ruch dolnych warstw cieczy podczas ruchu ciała stałego w niej. Lepkość pojawia się wtedy kiedy warstwy poruszają się z różnymi prędkościami

Transport energii

22. Średnia droga swobodna. Dyfuzja

Dyfuzja - wzajemne przenikanie się gazów , cieczy oraz ciał stałych w wyniku przemieszczania się cząsteczek jednego pomiędzy cząsteczki drugiego

W przypadku mieszaniny gazów przyczyną dyfuzji jest różnica koncentracji poszczególnych gazów w różnych częściach mieszaniny. Dyfuzja jest procesem wyrównywania koncentracji.

J= - ¹/₃
l Jn₀ / J_z

¹/₃
l współczynnik dyfuzji

Średnia droga swobodna

Średnia odległość jaką przebywają cząstki gazu bez zderzenia z innymi cząstkami. Średnia droga swobodna λ_m zależy od gęstości gazu ρ i od przekroju czynnego na zderzenia cząstek σ w następujący sposób

23. I zasada termodynamiki. Rodzaje przemian gazowych

W istocie zasada zachowania en. Zmiana energii wewnętrznej ciała lub układu ciał jest równa sumie wykonanej pracy oraz ciepła wymienionego z otaczjącymi ciałami.

ΔU = Q + W

dla układu istnieje taka funkcja stanu zwana en wewnętrzną , że zmiana tej en wywołana jest zmianą ciepła lub pracy

dU = dQ + dW

ENERGIA WEWNĘTRZNA suma en wszystkich cząsteczek plus en oddziaływań

Ciepło i praca dotyczy przepływu en.PRACA wykonana w jakimś procesie zależy od drogi. ENERGIA jest wlk niezależną, zależy jedynie od procesu

rodzaje przemian

przemiana POLITROPOWA (ciepło właściwe gazu =const.) odwracalny termodynamiczny proces zmiany stanu gazu, opisywany równaniem równanie ogólne dla 1 mola gazu dosk., ponieważ C=const, zatem

CdT = CvdT + pdV.

Rónanie różniczkowe tego procesu: dp/p+k(dV/V)=0 gdzie k- wykładnik politropowy, =(C-Cp)/(C-Cv); przekształcają go → ciepło właściwe: C=(Cp-kCv)/(1-k).

Przemiana adiabatyczna (dQ=0), przemiana zachodząca bez wymiany ciepła z otocz. Realizuje się bądź przez izolowanie cieplne układu, bądź przeprowadzając go bardzo szybko. Jeśli układ wykonuje pracę, to odbywa się to kosztem en wewnętrznej układu zatem temp jego obniża się.

Stosując I zasadę termodynamiki dla 1 mola gazu dosk. → CvdT= -pdV ; TV^χ-1=const , wyrażając T=pV (z równania Claperona)→ pV^χ =const. gdzie χ - stosunek ciepeł molowych, =Cp/Cv

Przemiana izotermiczna (T=const.)

Proces termodynamiczny podczas którego temp układu nie ulega zmianie, np. przemiany fazowe (topnienie, parowanie, sublimacja). Przemiany izotermiczne dla gazu doskonałego opisuje prawo Boyle'a- Mariotte'a

Z równania Claperona → p=(nRT / V). Ponieważ

T= const więc również nie ulega zmianie energia wewnętrzna, zatem dU = 0ΔQ = ΔW

Przemiana izochoryczna ( V =const.)

Proces termodynamiczny, podczas którego układ nie zmienia objętości, np. reakcje chemiczne zachodzące w gazach w zamkniętych naczyniach. W przemianie tej układ nie wykonuje pracy. Dla gazu doskonałego opisuje ta przemianę prawo Charlesa

dU=nCvdTΔQ = ΔU

Przemiana izobaryczna (p=const.)

Proces termodynamiczny podczas którego ciśnienie nie ulega zmianie np. reakcje chem zachodzące pod stałym ciśnieniem . praca wykonana przez gaz rozprężający się izobarycznie od obj V1 do V2 wynosi W = p(V2 - V1). Dla gazu doskonałego prawo Gay- Lussaca.

ΔQ = ΔU + ΔW

24. Ciepło molowe. Stopnie swobody

Ciepło molowe (pojemność cieplna) C - jest to iloczyn masy molowej  i danego ciepła właściwego c.

C =  c

Ciepło molowe przy stałej objętości niezależnie od rodzaju gazu wynosi

Cv = i / 2*R

a przy p = const.

Cp = (i + 2) / 2R

Ciepło molowe C wyrazi się w prosty sposób przez liczbę stopni swobody i.

Liczbą stopni swobody nazywamy liczbę niezależnych sposobów absorpcji en.

Stopnie swobody

Stopień swobody:

• jest to liczba niezależnych współrzędnych które są potrzebne do opisu cząstki lub atomu

• liczba możliwych ruchów niezależnych, które może wykonywać cząsteczka

gaz jednoatomowy i=3

gaz dwuatomowy i=5

gaz wieloatomowyi=6

25. Entropia. II zasada termodynamiki

II zasada termodynamiki określa nieodwracalność procesów makroskopowych przebiegających ze skończoną prędkością. Nie jest możliwy taki proces którego jedynym końcowym efektem jest otrzymanie pracy kosztem ciepła pobranego ze źródła o stałej temp. Ciepło nie może samorzutnie przejść z ciała o temp. niższej do ciała o temp. wyższej. Prawo to formułuje się jako prawo wzrostuENTROPII, w układzie odosobnionym wszystkie procesy zachodzą w taki sposób, że entropia układu wzrasta.

Trzy sformułowania 2-giej zasady Termodynamiki:

1)Entropowe: w układzie zamkniętym entropia nie maleje dS≥0 gdy >proc nie odwracalny gdy= stabilny

2)CLASIUSA: nie istnieje taki proces którego jedynym skutkiem jest przeniesienie ciepła z ciała zimnego do cieplejszego.

3)KELWINA - nie istnieje proces zmieniający całkowicie ciepło w prace.

Entropia: miano nie uporządkowania, jedna z funkcji stanu termodynamicznego. W dowolnym odwracalnym procesie termodynamicznym zachodzącym w stałej temp T zmiana entropii ΔS równa się ilorazowi dostarczonej ilości ciepła ΔQ i temp T

ΔS = ΔQ / T

w dowolnym nieodwracalnym procesie termodynamicznym entropia wzrasta. W temp zera bezwzględnego entropia dowolnego układu termod. w równowadze jest równa 0 (III zas. termodynamiki)

entropię można wyrazić jako:

S = k ln Ω

K stała Boltzmanowska

• liczba sposobów na ile może być realizowany dany układ termodynamiczny w określonych warunkach

układ pozostawiony sam sobie będzie miał pewną entropię. Cały układ może być realizowany na 2^N sposobów, przyjmie stan o możliwie największej entropii, realizowany na możliwie największej liczbie sposobów dąży do max nieuporządkowania. Obniżenie temp uporządkuje układ.

26. Funkcje stanu. Potencjały termodynamiczne

Funkcja stanu to w termodynamice funkcja zależna tylko od stanu układu. Nie zależy zatem od jego historii. Zmiana funkcji stanu zależy tylko od stanu początkowego i końcowego, a nie od rodzaju przemiany (równowagowej czy też nie), która do tej zmiany doprowadziła.
W praktyce stosuje się następujące funkcje stanu: energia wewnętrzna, energia swobodna, entalpia, entalpia swobodna, entropia, potencjał chemiczny oraz dla reakcji chemicznych stosuje się jeszcze stężenie molowe i aktywność molowa.

Potencjały termodynamiczne

27. III zasada termodynamiki

Zasada Nernsta- Plancka: entropia ciała maleje do 0, gdy temp. tego ciała zbliża się do 0 bezwzględnego, wynika z niej niemożność osiągnięcia 0 bezwzględnego. Entropia układu w temp 0 bezwzględnego jest stałą uniwersalną, którą można przyjąć za równą 0

S_T0 = 0

28. Dipol elektryczny

Układ dwóch równych co do wielkości ładunków elektrycznych, przeciwnego znaku zwykle w małej od siebie odległości, układ taki wytwarza wokół siebie pole elektryczne szybko malejące ze wzrostem odległości. Jeżeli odległość zmienia się periodycznie, wówczas dzięki zmianom pola elektrycznego związanym z ruchem ładunków, dipol jest źródłem fal elektromagnetycznych.

Jeden z najprostszych układów promieniujących, którego moment pędu zmienia się w czasie.

29. Prawo Gaussa dla pola elektrycznego

Strumień wektora indukcji elektrycznej przepływający przez dowolną powierzchnię zamkniętą jest równy ładunkowi jaki obejmowany jest przez ta powierzchnię.

POWIERZCHNIA GAUSSA - jest to dowolna powierzchnia zamknięta, którą przeprowadza się przez punkt w którym zaznacza się natężenie pola elektrycznego

Strumień indukcji Ф_D przez dowolną powierzchnię zamkniętą jest równy całkowitemu ładunkowi Σq zawartemu wewnątrz tej powierzchni: Ф_D= §Dds= Σq

Rozpatrzmy przypadek szczególny: pole E od pojedynczego ładunku. Strumień

ogólnie definiuje się : dФ_ε=EdA → Ф_ε=§EdA=E§dA

Ponieważ: E=F/q=Q/4πε_oR² , A=4πR² więc Ф_ε=EA=Q/ε_o

Porównują wzory otrzymujemy:

pole kuli: §EˉdAˉ=E§dA=EA=E4πx²=Q/ε_o Q=σ(4/3)πR³ E= σR³/3ε_ox²

pole naładowanej plyty: §EˉdAˉ=2EA=Q/ε_o Q=GA -> E=G/2ε_o

30. Energia pola elektrycznego

Można wykazać ogólnie, że jeżeli w przestrzeni istnieje pole elektryczne, to jest z nim związana pewna energia. Jeżeli w małym elemencie objętości  ΔV istnieje pole elektryczne E(r) , to energia tego pola jest równa

Początkowo nie naładowany kondensator ładuje się od 0 do napięcia U. Wtedy ładunek wzrasta od 0 do Q, gdzie Q = CU.

Praca zużyta na przeniesienie ładunku dq z okładki "-" na "+" wynosi

dW = Udq

Całkowita praca wynosi więc

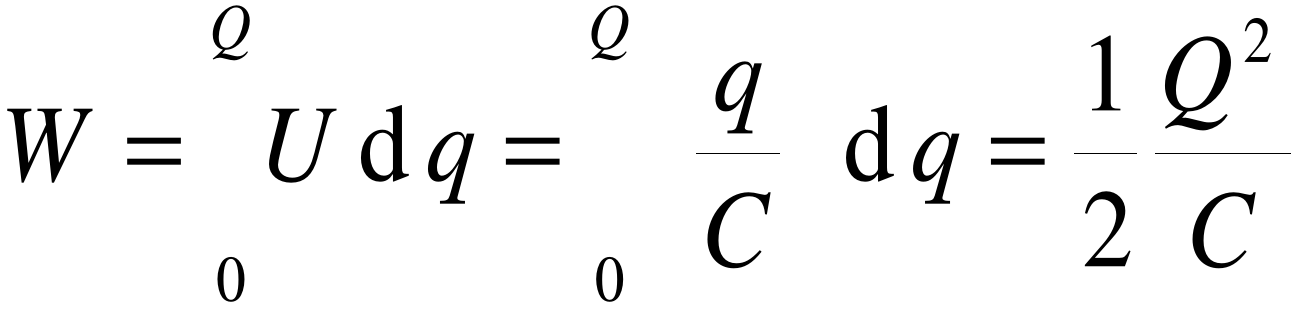
Dla kondensatora płaskiego

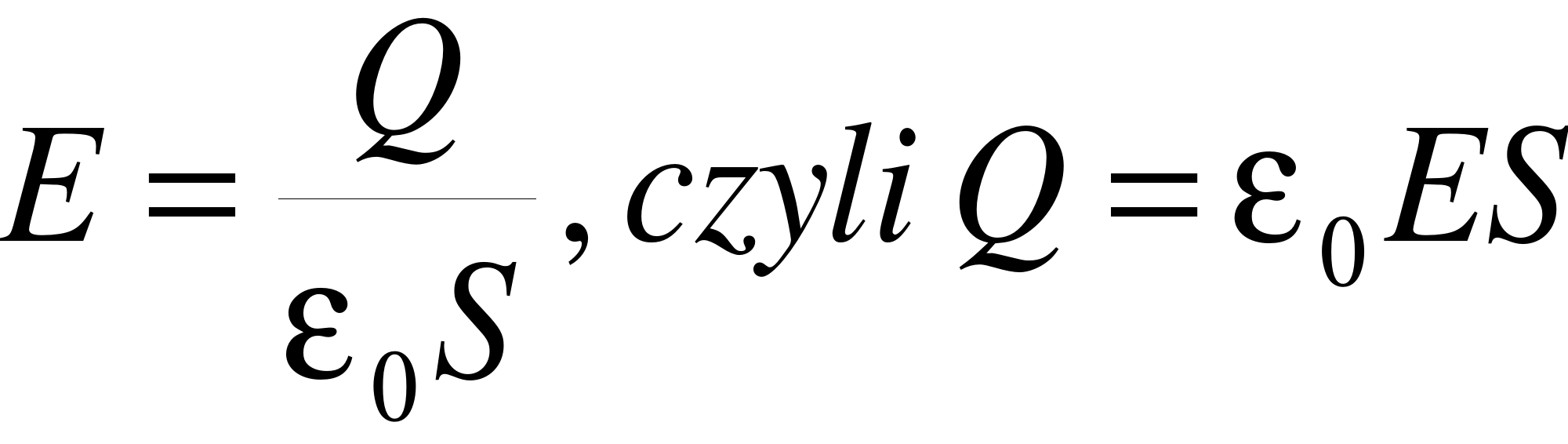
Podstawiamy to do wzoru na energię i otrzymujemy

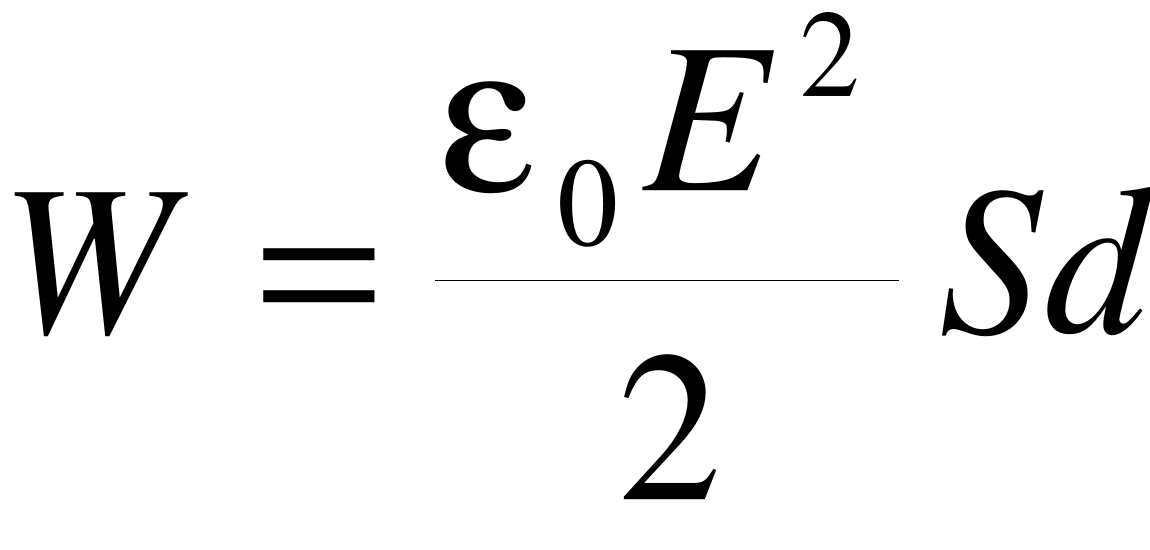
Podstawiając wyrażenie na C dostajemy

Sd - objętość kondensatora, więc gęstość energii w = W/Sd

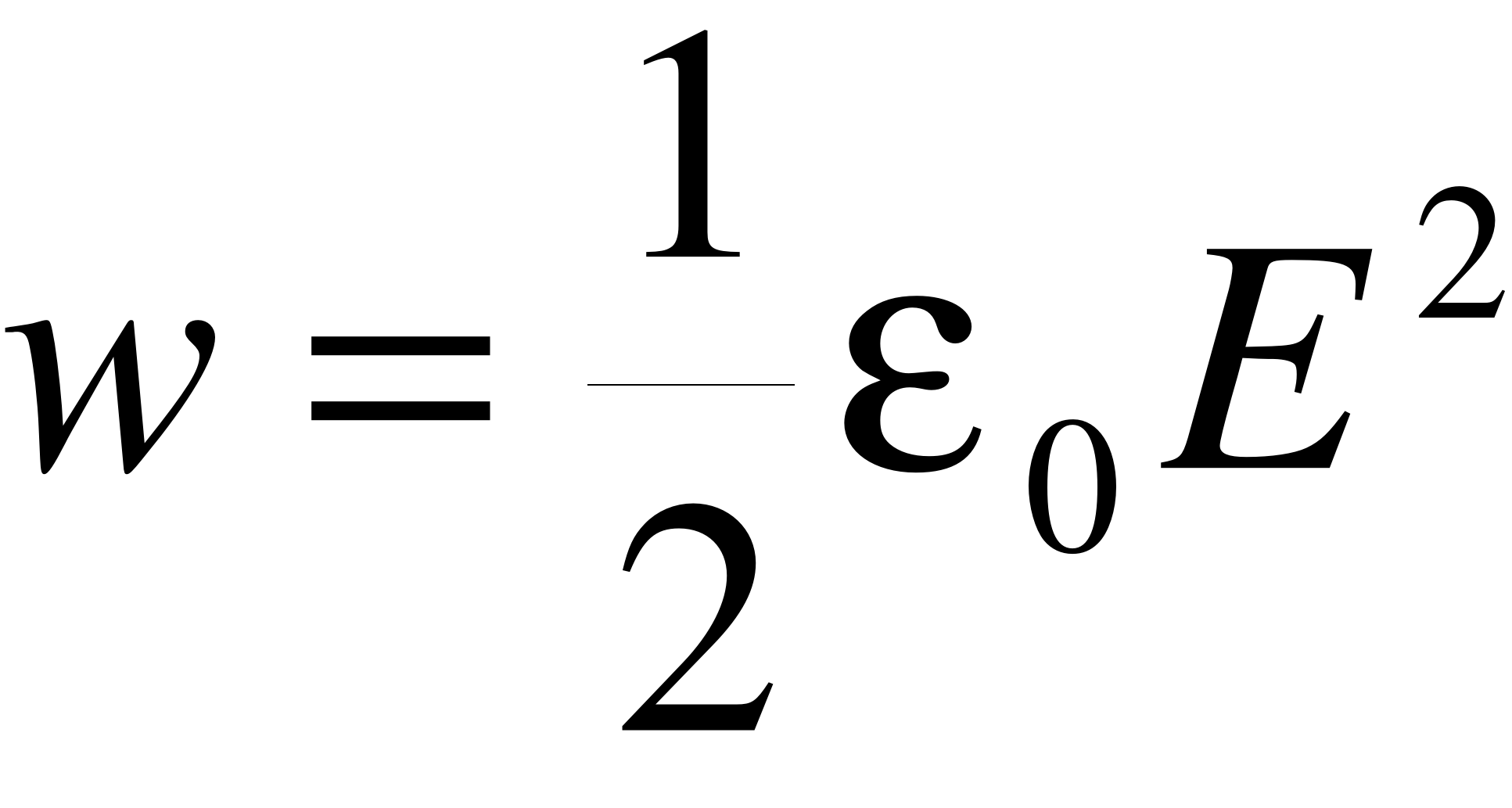
Jeżeli w jakimś punkcie przestrzeni jest pole E to możemy uważać, że jest tam zmagazynowana energia w ilości na jednostkę objętości.

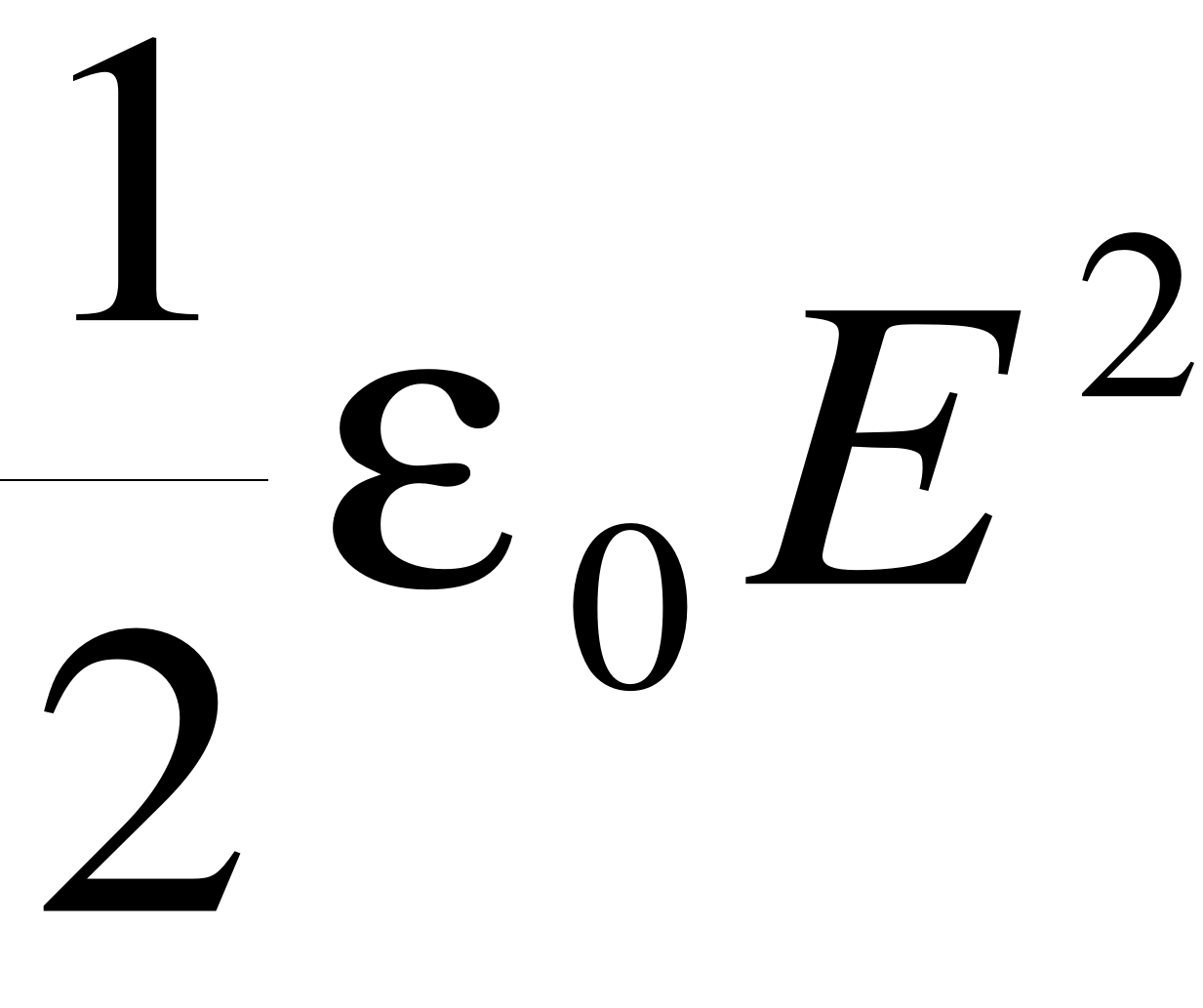
31. Pojemność elektryczna

Wielkość charakteryzująca zdolność ciała przewodzącego lub układu ciał przewodzących. Pojemność elektryczna dwóch ciał (elektron) tworzących kondensator jest to stosunek ładunku Q na jednej z elektrod do napięcia U między elektrodami:

C= Q/U [farad]

Zależy od kształtu i rozmiarów przewodnika oraz stałej dielektrycznej ε otaczającego ośrodka. Całkowita pojemność elektryczna równolegle połączonych kondensatorów elektrycznych równa jest sumie ich pojemności , w przypadku kondensatorów połączonych szeregowo zachodzi związek 1/C=Σ1/Ci

32. Prawa Kirchhoffa dla obwodów prądowych

1)W dowolnym węźle obwodu suma algebraiczna natężeń prądów wpływających i wypływających do węzła równa jest zeru: Σ Ii=0

2)W dowolnym oczku obwodu algebraiczna suma wszystkich sił elektromotorycznych i spadków napięć jest równa zeru, czyli: Σ i+ Σ IiR=0

33. Siła Lorenza. Ruch ładunku w polu magnetycznym

SIŁA LORENTZA Siła F z jaką pole elektromagnetyczne działa na poruszającą się cząstkę naładowaną

e ładunek elektryczny cząstki

E natężenie pola elektrycznego

B indukcja pola magnetycznego

V prędkość cząstki

c prędkość światła w próżni

pierwszy składnik wzoru przedstawia siłę działającą na cząstkę w polu elektrycznym, drugi siłę działającą w polu magnetycznym (ta ostatnia powoduje zakrzywienie toru cząstki). Działania siły Lorentza na elektrony w metalach i półprzewodnikach prowadzi do występowania zjawisk termomagnetycznych i galwanometrycznych.

RUCH ŁADUNKU W POLU

Jeżeli naładowana ruchoma cząstka znajdzie się w polu magnetycznym, to będzie na nią działać magnetyczny składnik siły Lorenza. Ruch ładunku w polu magnet. zależy od wartości prędkości oraz położenia wektorów v i B.

1.v=0 v v<>0   i   kąt(v,B) = 0 v 180 pole nie oddziaływuje na ładunek.

2.v<>0  i  v prostop do B  ? F=qvB.

Siła Lorenza jest siłą dośrodkową. Pod wpływem tej siły prędkość zmienia kierunek, lecz nie zmienia wartości prędkości - ładunek porusza się ruchem jednostajnym po okręgu.  qvB=(Ul*v^2)/r  to r=(Ul*v)/q*B  3.v<>0  i  kąt(v,B)= tu RYSUNEK. Złożeniem ruchów względem osi OB i Ovy jest ruch pospiralny;  OB-nie działa żadna siła; OVy-siła dośrodkowa powoduje ruch po okręgu   Vy=Vc*sin(alfa).

34. Strumień pola magnetycznego. Prawo Gaussa dla pola magnetycznego

Strumień pola magnetycznego
Jest to ilość linii przechodzących przez daną powierzchnię :

Strumień pola magnetycznego ma wartość 1 Webera, gdy przez powierzchnię 1 metra ustawioną ^ do linii pola przechodzą linie o indukcji 1 Tesli.

 strumień pola magnetycznego;

B natężenie pola elektromagnetycznego (indukcja);

S pole powierzchni

Prawo Gaussa dla pola magnetycznego
Strumień pola magnetycznego przechodzącego przez dowolną powierzchnię zamkniętą jest równy 0.

35. Prawo indukcji Faradaya

Zjawisko indukcji elektromagnetycznej polega na powstawaniu siły elektromotorycznej SEM w obwodzie podczas przemieszczania się względem siebie źródła pola magnetycznego i tego obwodu.

Mówimy, że w obwodzie jest indukowana siła elektromotoryczna (SEM indukcji). W obwodzie zamkniętym SEM indukcji wywołuje przepływ prądu indukcyjnego. 

Na podstawie powyższych obserwacji Faraday doszedł do wniosku, że o powstawaniu siły elektromotorycznej indukcji decyduje szybkość zmian strumienia magnetycznego B. Ilościowy związek przedstawia prawo Faradaya 

Jeżeli mamy obwód złożony z N zwojów to

36. Indukcja pola magnetycznego

Wektor indukcji magnetycznej B wlk charakteryzująca pole magnetyczne w ośrodku dia- para- ferro- magnetycznym

[tesl]

μ₀ przenikalność magnetyczna próżni

μ_r przenikalność względna ośrodka

H wektor natężenia pola magnetycznego umieszczenie ośrodka w polu magnetycznym powoduje jego namagnesowanie, w wyniku którego powstaje w nim dodatkowe pole magn.. natężenie wypadkowe pola magn. W ośrodku wynosi

I wektor namagnesowania

37. Obwody RLC. Rezonans w obwodach RLC

OBWODY RLC tradycyjny obwód zwiera indukcyjność L oraz pojemność C. Tymczasem każdy obwód ma pewien opór R, przykładowo jest to opór drutu z którego nawinięto cewkę. Obecność oporu w obwodzie powoduje straty energii w postaci wydzielającego się ciepła. Energia zawarta w obwodzie maleje i otrzymujemy drgania tłumione analogiczne do drgań tłumionych sprężyny, przy czym współczynnik tłumienia 1/2t jest równy R/2L.
Drgania w obwodzie RLC można podtrzymać jeżeli obwód będziemy zasilać napięciem sinusoidalnie zmiennym

REZONANS W OBWODACH RLC. Rezonansowy obwód, obwód elektryczny składający się z kondensatora i cewki indukcyjnej, w którym przez doprowadzenie zmiennego przebiegu elektrycznego są wzbudzane elektryczne drgania.

Prawa Kirhoffa w obwodzie zawierającym elementy R, L i C.

Obwód RL - narastanie i zanik prądu w solenoidzie.

Obwód LC - elektromagnetyczne drgania swobodne. Obwód RLC - elektromagnetyczne drgania tłumione

Obwód RL - narastanie i zanik prądu: U_R-U_L=ε IR+LdI/dt =ε dI/dt-(R/L)I-ε/L-0

u=RI/L-ε/L → du/dt=RdI/Ldt → dI/dT=Ldu/Rdt, Ldu/Rdt+u=0 du/u=-Rdt/L

lnu=-Rt/L+C u=Cexp(-Rt/L) RI/L-ε/L=Cexp(-Rt/L) dla t=0, I=0 → C= -ε/L

RI/L=(ε/L)(1-exp(-Rt/L)) I=I_o(1-exp(-Rt/L) - prąd narastania

IR+LdI/dt=0 dI/dt+RI/L=0 dI/dt=-RI/L dI/I= -Rdt/L → lnI=-Rt/L+C

I=Cexp(-Rt/L) dla t=0 I=I_o → C=I_o I=I_oexp(-Rt/L) - prąd zanikania

drgania tłumione w RLC: U_R+U_L+U_C=0 → (d/dt)(IR+LdI/dt+Q/C)=0

RdI/dt+Ld²I/dt²+I/LC=0 → d²I/dt²-(R/L)(dI/dt)+(I/LC)=0 (???) - analogiczne

równanie jak dla oscylatora tłumionego: 2β=R/L ω_o²=1/LC

I=I_oexp(-Rt/wL)cos(ωt+α)

c)obwód LC - elektryczne drgania swobodne U_C+U_L=0 LdI/dt+Q/C=0 →

(d/dt)(dI/dt)+Q/LC)=O d²I/dt²+(I/LC)=0 jest to równanie analogiczne jak dla

oscylatora swobodnego: I=I_Ocos(ω_ot+ α) → ω_o²=1/LC → ω_o=1/√(LC)

układ RLC - drgania wymuszone: U_R+U_L+U_C= ε → ε=IR+LdI/dt+Q/C

38. Prąd przesunięcia. Wirowe pole elektryczne i magnetyczne

PRĄD PRZESUNIĘCIA szybkość zmian w czasie wektora indukcji elektrycznej D ^,gęstość j wyraża się wzorem

E natężenie pola elektrycznego

ε₀ przenikalność elektr próżni

P polaryzacja dielektryku

Charakter prądu przesunięcia związany z polaryzacją dielektryku jpol jest taki jak prądu przewodzenia (obydwa są wywołane ruchem ład elektr), natomiast prąd związany ze zmianą natężenia pola elktr jpr ma charakter odmienny i nie prowadzi do wydzielenia ciepła Joule'a-Lenza. Wspólną cechą zarówno prądu przewodzenia, jak i jpr oraz jpol jest wytwarzanie wirowego pola magnetycznego.

WIROWE POLE

39. Równania Maxwella. Emisja fal elektromagnetycznych

Równania Maxwella:

1)
- uogólnione prawo indukcji Faradaya (zmienne pole magnetyczne wytwarza wirowe pole elektryczne które może wywołać prąd elektryczny) 2)
- uogólnione prawo Ampera ( prąd elektryczny lub zmienne pole elektryczne wytwarza wirowe pole magnetyczne)

3)
- (dla pola niejednorodnego) Prawo Gaussa dla pola elektrycznego (ładunek wytwarza pole elektrostatyczne o indukcji proporcjonalnej do kwadratu odległości, w przypadku dynamicznym może istnieć wirowe bezźródłowe pole elektryczne)

4)
- prawo Gaussa dla pola magnetycznego (nie istnieje w przyrodzie ładunek magnetyczny, linie indukcji są krzywymi zamkniętymi).

40. Hipoteza de'Broglie'a

HIPOTEZA O FALACH MATERII fale reprezentujące cząstki w ujęciu mechaniki kwantowej. Ruch każdej cząstki ma cechy falowe, przy czym długość fali cząstki swobodnej λ = h / p

H stała Plancka

P pęd cząstki

fale mogą być rozpatrywane jako fale prawdopodobieństwa, gdyż kwadrat ich amplitudy w danym punkcie przestrzeni określa gęstość prawdopodobieństwa znalezienia w tym pkt cząstki. Potwierdzenie słuszności tej hipotezy jest zjawisko dyfrakcji cząstek.

41. Postulaty mechaniki kwantowej

I POSTULAT Obiekt kwantowy może być opisany w postaci fali (paczki falowej). Kwadrat amplitudy tej fali określa prawdopodobieństwo znalezienia tej cząstki w danym miejscu w przestrzeni τ(x,t) ² = τ τ*

Największe prawdopodobieństwo znalezienia cząstki, jest tam gdzie en związana z falą jest największa (teoria probabilistyczna)

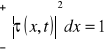
jeśli cząstka znajduje się w przestrzeni

II POSTULAT istnieją wlk kanoniczne sprzężone, których nie można wyznaczyć jednocześnie z dowolną dokładnością

Δx *Δp>= h

Δy*Δp_y >= h

Δϕ*ΔJz >= h

Δt*ΔE >= h wszystkie mają wymiar J * s

zasada nieokreśloności istnieje kwant działania równy stałej Planta przez 2 π ( nieokreśloność rzędu stałej Planta jest poniżej możliwości pomiarowych przyrządów, kwant działania jest b malutki)

II POSTULAT jeśli napiszę dla obiektu równanie, które nazywa się równaniem Schrodingera (równanie to sprawdziło się dla oscylatora harmonicznego) to rozwiązanie daje mi funkcję falową opisującą obiekt kwantowy. Jest to funkcja falowa opisująca falę płaską

równanie S dla jednego wymiaru

τ(x,t) = A e^i(kx-ωt)

p² / 2m = F

p = hk

h²k² / 2m = E = hω

42. Studnia potencjału- podstawowe wnioski i zastosowania

STUDNIA POTENCJAŁU, JAMA POTENCJAŁU obszar małej wartości potencjału otoczony obszarem dużej wartości potencjału (tzw. barierą potencjału), np. elektron w atomie znajduje się w studni potencjału. Ciało (cząstka) może się wydostać ze studni po otrzymaniu z zewnątrz energii.

Potencjał nieskończenie głębokiej prostokątnej studni ma tę własność, że wiąże cząstkę o skończonej energii E  0. W mechanice klasycznej dozwolona jest dowolna wartość energii, natomiast w mechanice kwantowej dozwolone są tylko pewne dyskretne wartości własne En. Dla niezbyt dużych wartości liczby kwantowej n odpowiadające im wartości własne i funkcje własne użyte być mogą jako przybliżenie odpowiadających im wartości własnych i funkcji własnych dla potencjału o dużym, lecz skończonym V0.

---