EGZAMIN
16 czerwca 2003
Podstawowe struktury danych
Z ilu wartości elementarnych składają się poniższe struktury:
Pierwsza z 1224, druga z 3.
Pierwsza z 1224, druga z 2.
Pierwsza z 36, druga z 3.
Pierwsza z 36, druga z 2.
Array[-1..10] of record A: array[Boolean] of 1..100; B: integer; C: char; End; Record case Boolean of False: (i1, i2: integer); True: (i3: integer); End; |
Poniższy algorytm oblicza ujemne potęgi liczby 2 i wypisuje je na ekranie. Zdefiniuj podany algorytm w postaci procedury lub funkcji z argumentami oraz zmień algorytm tak, żeby wypisanie ujemnych potęg liczby 2 było zrealizowane nie w procedurze (lub funkcji), a w programie głównym. Wykorzystaj do tego argumenty procedury (lub funkcji).
program abc; const n=10; type cyfra = 0..9; var i, k, r: integer; d: array[1..n] of cyfra; begin for k:=1 to n do begin write(`.'); r:=0; for i:=1 to k-1 do begin r:=10*r + d[i]; d[i]:=r div 2; r:=r - 2*d[i]; write(chr(d[i]+ord(`0'))) end; d[k]:=5; writeln(`5'); end; end. |
Pracownicy pewnej księgarni prowadzą komputerową kartotekę, w której umieszczają tytuł i nazwę wydawnictwa każdej sprzedanej książki. Dane trafiają do kartoteki w tej samej kolejności, w której książki są sprzedawane. Co dwa tygodnie właściciel księgarni oblicza ręcznie, ile sprzedano egzemplarzy każdego tytułu oraz książek każdego wydawcy. Następnie grupuje wyniki obliczeń według alfabetycznej listy wydawnictw i korzysta z nich przy zamawianiu kolejnych dostaw. Proszę o stworzenie programu wykonującego powyższe zadanie zgodnie z poniższym wzorcem..
Program prog;
Procedure wczytywanie; Begin Writeln(”Wczytywanie”); End;
Procedure sortowanie; Begin Writeln(”Sortowanie”); End;
Procedure zliczanie; Begin Writeln(”Zliczanie”); End;
Procedure drukowanie; Begin Writeln(”Drukowanie”); End;
Begin
Wczytywanie;
Sortowanie;
Zliczanie;
Drukowanie;
End.
Zaznacz poprawne definicje typów.
Odcinek = 0..1.0;
Zakres = -0.1E20..+0.1E20;
Znaki = 'a'..'9';
T = 7..7;
Figura = (trojkat, okrag, prosta, okrag);
Poniżej dany jest algorytm przeszukiwania połówkowego. Zdefiniuj ten algorytm za pomocą procedury z argumentami dotyczącymi tablicy a i zastąp w nim pętlę repeat pętlą while. Wywołaj procedurę w programie głównym.
program progA; const n=10; type cyfra = 0..9; var i, j, k: integer; a: array[1..n] of cyfra; begin i:=1; j:=n; repeat k:=(i+j) div 2; if a[k] < x then i:=k else j:=k; until (a[k]=x) or (i>=j); end. |
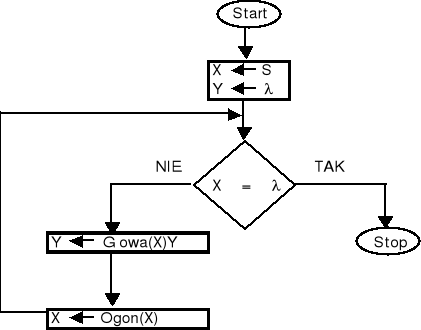
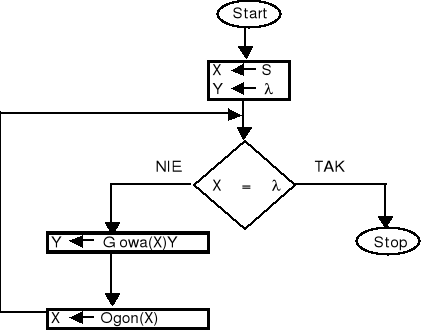
Zapisz poniższy algorytm w postaci programu komputerowego. S jest tekstem, lambda jest tekstem pustym, Głowa(X) jest operacją pobrania pierwszego znaku z tekstu X, Ogon(X) jest operacją usunięcia pierwszego znaku z tekstu X.
|
Po wykonaniu poniższego programu zostaną wypisane następujące liczby:
0 i 2
1 i 2
0 i 0
1 i 0
Program p; Var i, j: integer; Procedure q(x: integer; var y: integer); Begin x:=y+1; y:=x+1; End; Begin i:=0; j:=0; q(i,j); Write(i: 2, j: 2); End. |
Sortowanie
Niech będą dane trzy algorytmy sortowania (Sortowanie stogowe, Sortowanie metodą Shella, Sortowanie przez proste wstawianie). Które z nich są stabilne?
Tylko sortowanie metodą Shella.
Tylko sortowanie metodą Shella i przez proste wstawianie.
Tylko sortowanie stogowe.
Wszystkie wymienione.
Poniżej dany jest wektor liczb i jego zmiany w trakcie realizacji sortowania. Co to za algorytm sortowania?
Przez proste wstawianie
Przez proste wybieranie
Przez prostą zamianę
4, 3, 5, 6, 7, 1, 2 1, 3, 5, 6, 7, 4, 2 1, 2, 5, 6, 7, 4, 3 1, 2, 3, 6, 7, 4, 5 1, 2, 3, 4, 7, 6, 5 1, 2, 3, 4, 5, 6, 7 |
Poniżej dany jest algorytm sortowania przez wstawianie połówkowe. Algorytm ten będzie działał nadal poprawnie, jeżeli:
W instrukcji while warunek l<=p zostanie zastąpiony warunkiem l<p
Instrukcja p:=m-1; zostanie zastąpiona przez p:=m;
Instrukcja l:=m+1; zostanie zastąpiona przez l:=m;
procedure wstawianiePolowkowe; var i, j, l, p, m: index; x: obiekt; d: array[1..n] of cyfra; begin for i:=2 to n do begin x:=a[i]; l:=1; p:=i-1; while l<=p do begin m:=(l+p) div 2; if x.klucz<a[m].klucz then p:=m-1 else l:=m+1 end; for j:=i-1 downto l do a[j+1]:=a[j]; a[l]:=x; end; end. |
Algorytmy rekurencyjne
Przy założeniu, że n jest liczbą całkowitą nieujemną, poniższy algorytm wykonuje:
Sumowanie wartości zmiennych indeksowanych x[1], x[2], ..., x[n].
Sumowanie wartości zmiennych indeksowanych x[1], x[2], ..., x[n-1].
Sumowanie wartości zmiennych indeksowanych x[0], x[2], ..., x[n].
Sumowanie wartości zmiennych indeksowanych x[0], x[2], ..., x[n-1].
function abc(x: tablica; n: integer); begin if n=0 then abc:=0 else abc:=x[n] + abc(n-1); end; |
Sprawdź rekurencyjnie, czy słowo jest palindromem.
Poniżej dany jest algorytm obliczający wartość funkcji silnia. Czy obie wersje są równoważne?
tak
nie
function silnia(n: integer): integer; var i, s: integer; begin i:=0; s:=1; while i>n do begin i:=i+1; s := i * s; end; silnia := s; end; |
function silnia(n: integer): integer; var i, s: integer; begin if n>0 then silnia := n * silnia(n-1) else silnia := 1; end |
Dynamiczne struktury informacyjne
Poniżej dana jest funkcja wykonująca pewną operację na liście L. Niech head[L] będzie operacją, która zwraca początek listy, key[x] operacją, która zwraca klucz elementu listy wskazywanego przez wskaźnik x, a next[x] operacją, która zwraca wskaźnik do następnego elementu listy w stosunku do elementu wskazywanego przez wskaźnik x. Co ona wykonuje?
funkcja LIST (L, k) argumenty wejściowe: L - lista, k - klucz; zwraca: ? x := head[L] dopóki x<>NIL i key[x] <>k x := next[x] koniec dopóki zwróć x
|
Pokaż, jak odwrócić listę (w miejscu). Zmień na przykład listę (A, B, C, D) na (D, C, B, A). Zapisz algorytm w postaci procedury.
Odwróć zawartość stosu używając jednej pomocniczej kolejki
Napisz program, który korzystając z kolejki lub stosu dokona konwersji liczby z zapisu dziesiętnego na dwójkowy
Poniżej dane są: definicja drzewa i procedura znajdująca element drzewa o danym kluczu x i wykonująca na nim określoną operację. Zamień w procedurze search instrukcję while na instrukcję repeat.
Type wsk = ^drzewo; drzewo = record klucz: integer; lewe, prawe: wsk; end;
|
Function search (node: wsk, key: integer): wsk; Var znaleziony: boolean; Begin Znaleziony := false; while (node <> nil) and not znaleziony do begin if (key = node^.klucz) then znalzeiony := true else if (key < node^.klucz) node := node^.lewe; else node := node^.prawe; end; write(node^.klucz); search:=node; end; |
Narysuj drzewo powstałe w wyniku działania poniższego algorytmu z wczytanego ciągu liczb (3, 7, 5, 9, 15, 8, 27, 53, 45, 13, 11). Jakie ciągi węzłów otrzymamy drukując drzewo? Podaj ciągi otrzymane w procedurze drukowania, gdyby w trakcie drukowania było wywołane przeglądanie wzdłużne, poprzeczne i wsteczne.
PROGRAM budujDrzewo; TYPE typElementu = integer; wskaznik = ^wezel; wezel= record klucz: typElementu; lewy, prawy: wskaznik; end; VAR n: integer; korzen: wskaznik; FUNCTION drzewo(n: integer): wskaznik; VAR nowyWezel: wskaznik; x, nl, np: integer; Begin if n=0 then drzewo:=nil else begin nl:=n div 2; np:=n-nl-1; read(x); new(nowyWezel); with nowyWezel^ do begin klucz:=x; lewy := drzewo(nl); prawy := drzewo(np); end; drzewo := nowyWezel; end; End; PROCEDURE drukujDrzewo(t: wskaznik; h: integer); VAR i: integer; Begin if t<>nil then with t^ do begin drukujDrzewo(lewy, h+1); for i:=1 to h do write (' '); writeln(klucz); drukujDrzewo(prawy, h+1) end; End; Begin read(n); korzen := drzewo(n); drukujDrzewo(korzen, 0); End. |
Wyszukiwarka
Podobne podstrony:
kolokwia egzaminy 2003 2005
I kolokwium, Informatyka PWr, Algorytmy i Struktury Danych, Algorytmy i Struktury Danych, kolokwia i
I kolokwium(1), Informatyka PWr, Algorytmy i Struktury Danych, Algorytmy i Struktury Danych, kolokwi
II1 kolokwium, Informatyka PWr, Algorytmy i Struktury Danych, Algorytmy i Struktury Danych, kolokwia
I1 kolokwium, Informatyka PWr, Algorytmy i Struktury Danych, Algorytmy i Struktury Danych, kolokwia
II kolokwium, Informatyka PWr, Algorytmy i Struktury Danych, Algorytmy i Struktury Danych, kolokwia
Kolokwia,egzaminy, Dzienni07, Wyniki z zaliczenia ćwiczeń i wykładów z Genetyki i hodowli roślin ogr
Wymagania do kolokwium zaliczeniowego oraz egzaminu
II kolokwium(1), Informatyka PWr, Algorytmy i Struktury Danych, Algorytmy i Struktury Danych, kolokw
kolokwia egzaminy 2003 2005
fizjologia kolokwium zaliczeniowe 2006stoma
Zagadnienia do kolokwium zaliczeniowego 2013-2014, Inżynieria materiałowa pwr, Inżynieria chemiczna
WARIANT C, FIR UE Katowice, SEMESTR IV, Ubezpieczenia, chomik, Ubezpieczenia (kate evening), Ubezpie
Zadania egzaminacyjne 2003, Nieorganiczna, chemia2, Arkusze powtórzeniowe, Pobieranie1, studia 1.2,
Kolokwia, egzaminy Mercik kolokwium ćwiczenia
Zagadnienia do opracowania na kolokwium zaliczeniowe2
Kolokwium zaliczeniowe
Wyniki kolokwium zaliczeniowego z kompleksowej ochrony lasu dla studentów III roku OZL, Dokumenty se
egzamin z diagnostyki zaocznych, Zaliczenia diagnostyka
więcej podobnych podstron