STATYKA
1. Zasady statyki
Zasada pierwsza (zasada równoległoboku) - działanie dwóch sił P1 i P2 można zastąpić działaniem jednej siły R, działającej na ten sam punkt i będącej przekątną równoległoboku ABCD zbudowanego na wektorach sił P1 i P2. ![]()
Gdy siły P1 i P2 działają wzdłuż jednej prostej i są zgodnie skierowane to R= P1+P2.
Natomiast, gdy siły są przeciwnie skierowane i P2>P1 to R= P1-P2.
Zasada druga - jeżeli do ciała przyłożone są dwie siły, to równoważą się one tylko wtedy gdy mają te samą linię działania, te same wartości liczbowe i przeciwne zwroty. Aby siły te równoważyły się, muszą być spełnione zależności: ![]()
i ![]()
. Na podstawie tej zasady można, wyprowadzić pojęcie siły zerowej, czyli siły, której wartość jest równa zeru. Z zasady tej wynika także pojęcie siły przeciwnej do siły P1, której bezwzględna wartość oraz linie działania są takie same, ale zwrot jest przeciwny. Siłę przeciwną oznacza się ze znakiem minus (-P2).
Zasada trzecia - skute działania układu sił przyłożonego do ciała nie zmienia się, jeśli do tego układu dodamy lub odejmiemy dowolny układ równoważących się sił, czyli tzw. układ zerowy. Z zasady tej wynika następujący wniosek: każdą siłę działającą na ciało sztywne można przesunąć dowolnie wzdłuż jej linii działania.
Zasada czwarta (zasada zesztywnienia) - jeżeli ciało odkształcalne znajduje się w równowadze pod działaniem pewnego układu sił, to również pozostanie w równowadze ciało odkształcalne sztywne (nieodkształcalne) identyczne z poprzednim, pod działaniem tego samego układu sił. Wynika stąd wniosek, że warunek konieczny i wystarczający do równowagi ciała sztywnego jest tylko warunkiem koniecznym, ale nie wystarczającym do równowagi ciała odkształcalnego.
Zasada piąta (zasada działania i przeciwdziałania) - każdemu działaniu towarzyszy równe co do wartości, o przeciwnym zwrocie i leżące na tej samej prostej przeciwdziałanie.
Zasada szósta (zasada oswobodzenia od więzów) - każde ciało nie swobodne można myślowo oswobodzić z więzów, zastępując ich działanie reakcjami, a następnie rozważać jako ciało swobodne znajdujące się pod działaniem sił czynnych i biernych (reakcji więzów).
2. Prawa Newtona
I Prawo Newtona Jeżeli na ciało nie działają żadne siły lub działające siły równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym po lini prostej.
II Prawo Newtona Jeżeli na ciało działa siła (wypadkowa wszystkich sił działających na punkt materialny jest różna od zera), to porusza się ono względem inercjalnego układu odniesienia ruchem zmiennym z przyspieszeniem wprost proporcjonalnym do siły, a odwrotnie proporcjonalnym do masy ciała. Kierunek i zwrot wektora przyspieszenia są zgodne z kierunkiem i zwrotem wektora siły.
![]()
![]()
III Prawo Newtona Jeżeli dwa ciała A i B działają wzajemnie na siebie, to siła ![]()
AB, z jaką ciało A działa na ciało B i siła ![]()
BA, z jaką ciało B działa na ciało A, są równe co do wartości, mają ten sam kierunek, ale przeciwne zwroty![]()
AB= -![]()
BA
3. Stopnie swobody, więzy i ich oddziaływania
Więzami nazywamy warunki, które nakładają ograniczenia na ruch ciała lub jego położenie w przestrzeni. Jeżeli ograniczenia te dotyczą ruchu ciała (prędkości, przyśpieszenia), to mamy do czynienia z więzami kinematycznymi; natomiast gdy ograniczenia dotyczą położenia ciała w przestrzeni, to takie więzy nazywamy więzami geometrycznymi.
Każde ciało sztywne można myślowo uwolnić od więzów, jeżeli zastąpi się działanie więzów odpowiednimi reakcjami, a następnie rozpatrywać je jako ciało swobodne znajdujące się pod działaniem sił czynnych i reakcji więzów (sił biernych).
Rodzaje podpór:
Podpora przegubowa przesuwna:
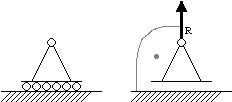
Jedna niewiadoma reakcja R.
Podpora przegubowa stała:
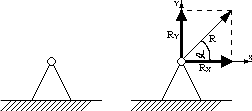
Dwie niewiadome reakcje Rx i Ry ( lub R i α )
Zawieszenie na cięgnach wiotkich:
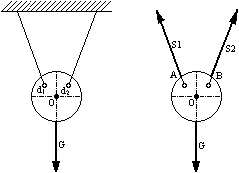
Dwie niewiadome S1 i S2
Podparcie na gładkiej lub chropowatej powierzchni:
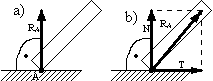
a) więzły idealne
b) więzły normalne ( z tarciem )
Utwierdzenie sztywne:
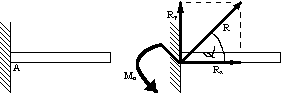
Trzy niewiadome Rx, Ry i Mo ( moment utwierdzenia )
Pręt przegubowy:
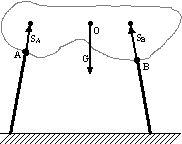
Po jednej niewiadomej na każdy pręt
Przegub kulisty
Łożysko szyjne
Łożysko oporowe lub stopowe
Zawias
Usztywnienie całkowite
4. Moment siły względem punktu, zmiana bieguna redukcji
Momentem siły względem punktu (nazwanego punktem „O”) nazywamy wektor momentu ![]()
O równy iloczynowi wektorowemu promienia ![]()
wyprowadzonego z punktu O do wektora ![]()
i wektora siły ![]()
.
![]()
O ![]()
=![]()
![]()
![]()
Zwrot ![]()
O zgodny z regułom śruby prawoskrętnej.
![]()
![]()
Jego kierunek (![]()
O) jest prostopadły do płaszczyzny utworzonej przez wektory![]()
i ![]()
.
Jego wartość jest równa ![]()
=Fd.
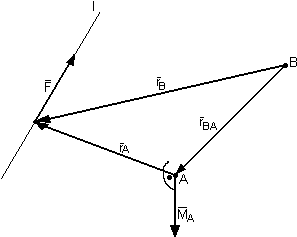
Zmiana bieguna (punktu O) momentu siły
Moment względem punktu A:
![]()
Moment względem punktu B:
![]()
Patrz rysunek - dodawanie wektorów metodą trójkąta:
![]()
![]()
![]()
Moment siły względem punktu B jest równy sumie dwóch momentów, z których jeden obliczany jest względem dowolnego punktu, natomiast drugi jest momentem tej siły uczepionym w punkcie A liczonym względem punktu B.
5. Moment siły względem osi
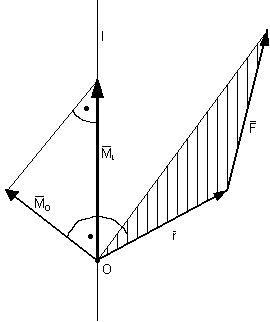
Momentem siły ![]()
względem dowolnej prostej l nazywamy rzut, wektora momentu obliczanego względem dowolnego punktu leżącego na prostej l, na prostą l.
6. Para sił
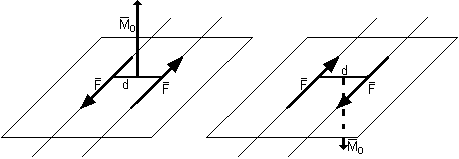
Układ dwóch sił równoległych o takich samych wartościach liczbowych lecz przeciwnie zwróconych nazywamy parą sił.
Wypadkowa pary sił równa się zero, czyli pary sił nie można zastąpić jedną siłą.
Oddziaływanie pary sił wyraża się momentem pary sił.
Momentem pary sił - jest wektor prostopadły do płaszczyzny działania pary sił, o wartości równej iloczynowi wartości siły i ramienia, o zwrocie zgodnym z regułą śruby prawo skrętnej. ![]()
Własności pary sił:
- Dwie pary sił o tej samej płaszczyźnie działania są sobie równe, gdy posiadają równe momenty.
- Zachowując niezmieniony moment, parę sił można przenieść do dowolnej płaszczyzny równoległej do jej płaszczyzny działania nie zmieniając równowagi układów.
- Dwie pary sił działające w jednej płaszczyźnie można zastąpić przez jedną parę sił, działającą w tej samej płaszczyźnie o momencie równym sumie momentów dwóch par sił.
- Dwie pary sił działające w przecinających się płaszczyznach są równoważne jednej parze sił o momencie równym wektorowej sumie momentów tych par.
7. Redukcja i równowaga dowolnego przestrzennego układu sił
Elementy redukcję dowolnego płaskiego układu sił:
- wektor główny Fg,
- moment główny Mg,
- parametr układu tzw. wyróżnik k
Wektor główny - równy jest sumie geometrycznej wszystkich sił układu traktowanych jako wektory swobodne. Wektor główny nie zależy od bieguna do którego redukujemy układ sił. ![]()
![]()
Moment główny (ogólny) - równy jest sumie momentów wszystkich sił względem bieguna redukcji O. Moment główny zależy od wyboru bieguna. ![]()
Parametr układu (wyróżnik) - to iloczyn skalarny wektora głównego i momentu ogólnego.
![]()
, czyli: ![]()
k≤0
Przypadki redukcji dowolnego układu sił.
Wektor główny |
Moment główny |
Parametr układu k |
Wynik redukcji |
=0 |
=0 |
=0 |
Ukł. w równowadze |
=0 |
≠0 |
=0 |
Para sił |
≠0 |
=0 |
=0 |
Wypadkowa |
≠0 |
≠0 |
≠0 |
Skrętnik, dwie siły skośne |
Warunki równowagi dowolnego płaskiego układu sił
Dowolny płaski układ sił jest w równowadze jeśli algebraiczne sumy wszystkich rzutów sił na osie układu i suma momentów wszystkich sił względem dowolnie obranego bieguna na płaszczyźnie działania tych sił są równe zeru.
Warunki równowagi dowolnego przestrzennego układu sił
Przestrzenny dowolny układ sił znajduje się w równowadze jeżeli algebraiczne sumy rzutów wszystkich sił na trzy osie układu współrzędnych i algebraiczne sumy momentów wszystkich sił względem tych osi są równe 0.
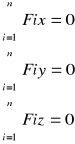
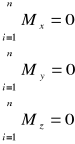
8. Redukcja sił wewnętrznych w prętach płaskich
Siły wewnętrzne w prętach płaskich i prostych.
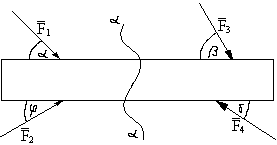
Pręty płaskie - leżą na płaszczyźnie (nie mają przekroju).
W prętach płaskich wyróżniamy jedynie siły wzdłużne ![]()
, siły poprzeczne ![]()
i moment gnący ![]()
.
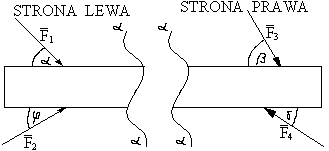
Aby wyznaczyć siły wewnętrzne należy dokonać myślowego przekroju i obliczyć siły i momenty dla jednej strony.
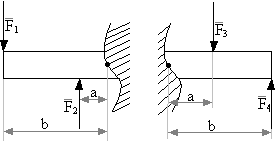
Siłą wzdłużną inaczej normalną ![]()
w danym przekroju α-α, nazywamy sumę rzutów wszystkich sił znajdujących się po jednej stronie przekroju na kierunek styczny do osi przekroju. Siłę wzdłużną uważamy za dodatnią jeżeli działa od
rozważanego przekroju, czyli powoduje rozciąganie pręta. Natomiast siła działająca do przekroju pręta jest siłą ujemną powodującą ściskanie pręta.
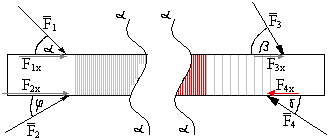
A więc dla rysunku obok dla lewej strony:
![]()
=![]()
natomiast dla prawej:
![]()
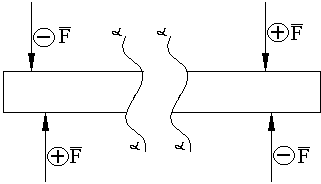
Siłą poprzeczną przekroju α-α, nazywamy sumę rzutów wszystkich sił znajdujących się po jednej stronie przekroju na kierunek prostopadły do stycznej do osi pręta lub prostopadły do osi pręta w przypadku prętów prostych. Siłę poprzeczną uważamy za dodatnią jeżeli rozpatrując lewą część pręta siła będzie skierowana do góry, w pozostałych siła będzie miała znak przeciwny. Po stronie prawej siła skierowana do góry znak ujemny, a siła kierowana na dół dodatni. Znak siły zależy od strony dla której badamy przekrój.
![]()
Momentem gnącym w danym przekroju α-α nazywamy sumę momentów wszystkich sił znajdujących się po jednej stronie przekroju, liczonych względem tego przekroju. Moment gnący uważamy za dodatni jeżeli powoduje wygięcie pręta wypukłością w dół, natomiast za ujemny jeżeli powoduje wygięcie pręta wypukłością do góry. Znak momentu nie zależy od wyboru strony rozważanego przekroju.
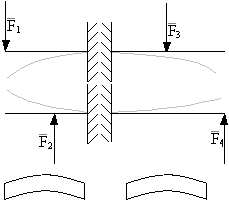
WNIOSKI
- Jeżeli na pewnym odcinku belki występuje obciążenie ciągłe q to wykresem sił poprzecznych T na tym odcinku jest prosta nachylona pod kątem do osi belki, natomiast wykresem momentów gnących jest parabola.
- Jeżeli na pewnym odcinku belki nie występuje obciążenie ciągłe to wykresem sił poprzecznych T jest prosta równoległa do osi belki i T=const. Natomiast wykresem momentów gnących jest prosta nachylona pod kątem do osi pręta.
- Moment gnący osiąga ekstremalne wartości w miejscach zerowania siły poprzecznej.
- W miejscu działania siły skupionej na wykresie sił poprzecznych wystąpi nieciągłość siły poprzecznej objawiająca się skokiem o wartość siły skupionej. W przekroju w punkcie przyłożenia momentu skupionego na wykresie Mg wystąpi skok o wartość momentu.
- Jeżeli na brzegach belki nie występuje moment skupiony - to wartość momentu w punktach brzegowych jest równa 0.
9. Zależności różniczkowe między siłami wewnętrznymi
Wzory Schedlera - zależności różniczkowe między siłami w pręcie:
Pochodna momentu gnącego względem współrzędnej osi pręta jest równa sile poprzecznej:
![]()
Druga pochodna momentu gnącego względm współrzędnej osi pręta jest równa natężeniu obciążenia ciągłego:
![]()
Pochodna siły poprzecznej względm wsółrzędnych osi pręta równa się natężeniu obciążenia ciągłego:![]()
10. Tarcie i prawa tarcia
Tarciem nazywamy zjawisko powstawania sił stycznych do powierzchni styku dwu ciał. Są to siły bierne. Tarcie występuje między stykającymi się ciałami stałymi, spowodowane jest działaniem siły normalnej dociskającej te ciała oraz siły stycznej przemieszczającej je względem siebie (tarcie kinetyczne) bądź te usiłującej je przemieścić (tarcie styczne)
Tarcie spoczynkowe - przeciwdziała sile która działa na ciało i chce je wyprowadzić ze stanu spoczynku.
Tarcie kinetyczne - występuje tylko w czasie ruchu.
Rodzaje tarcia:
Tarcie ślizgowe ciała sztywnego o powierzchnię płaską
F=T N=G ΣFix=0 ΣFiy=0
T=<μN spoczynek μ - współczynnik tarcie statycznego
T=μN tarcie rozwinięte
T=μkN ruch μk - współczynnik tarcie kinetycznego
Tarcie toczne to opór toczenia ciała sztywnego w kształcie walca po powierzchni płaskiej. Tarcie toczne jest momentem, a nie siłą jak tarcie statyczne N*f [Nm]
F-T0=0
N-Q=0
Nf-Fr=0 f - współczynnik tarcia tocznego
Prawa tarcia
- Siła tarcia jest niezależna od wielkości powierzchni stykających się ze sobą a zależy tylko od ich rodzaju.
- Wartość siły tarcia dla ciała znajdującego się w spoczynku może zmieniać się od zera do granicznej wartości proporcjonalnej do całkowitego nacisku ciała.
- Gdy ciało ślizga się po powierzchni siła tarcia jest przeciwnie skierowana do kierunku ruchu i jest mniejsza od wartości granicznej.
KINEMATYKA
1. Kinematyka punktu, prędkość i przyspieszenie punktu
Opis ruchu punktu, układu punktów, bryły sztywnej lub układów brył sztywnych, bez wnikania w przyczyny ruchu. Wielkościami charakteryzującymi ruch są: przemieszczenie, prędkość, przyspieszenie.
x=f(t) y=f(t) z=f(t)
vx=dx/dt vy=dy/dt vz=dz/dt
ax=d2x/dt2 ay=d2y/dt2 az=d2z/dt2
Prędkość pkt materialnego:
- wektor prędkości pkt w danej chwili jest równy pochodnej wektora promienia wodzącego względem czasu
- wektor prędkości v pkt leży na stycznej do toru i ma kierunek ruchu pkt A
Przyspieszenie pkt bryły materialnej to całkowite przyspieszenie dowolnego pkt bryły sztywnej poruszającej się ruchem obrotowym jest wektorową sumą 2 przyspieszeń: przyspieszenia stycznego (obrotowego), przyspieszenia normalnego (dośrodkowego)
Przyspieszenie styczne atA=εR[m/s2] kierunek wektora przyspieszenia stycznego jest kierunkiem stycznym do toru rozpatrywanego pkt. Zwrot zależy od tego czy ruch jest przyspieszony czy opóźniony. Jeżeli jest przyspieszony to zwrot wektora przyspieszenia stycznego jest zgodny ze zwrotem toru rozpatrywanego pkt.
Przyspieszenie normalne anA=ω2R kierunek wektora przyspieszenia normalnego jest prostopadły do kierunku wektora prędkości kątowej (prostopadły do osi obrotu) i prostopadły do wektora prędkości liniowej rozpatrywanego pkt czyli pokrywa się z promieniem okręgu po którym w danej chwili porusza się rozpatrywany pkt.
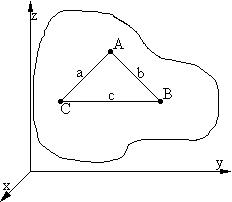
2. Kinematyka bryły sztywnej
Położenie bryły w przestrzeni określone przez trzy punkty.
A(xA, xA, xA)
B(xB, xB, xB)
C(xC, xC, xC)
Równania maja postać:
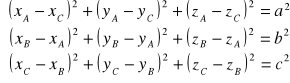
Bryły sztywne mogą wykonywać:
- ruch postępowy (ruch jednoparametrowy)
- ruch obrotowy
- ruch płaski
- ruch kulisty
- ruch złożony (względny)
- ruch ogólny
3. Ruch postępowy ciała sztywnego
To ruch w którym wszystkie punkty bryły doznają tych samych przesunięć. Jest to najprostszy przypadek ruchu bryły sztywnej zwany jednoparametrowym (wystarczy podać tylko jedną wielkość określającą ruch aby jednoznacznie opisać ruch bryły).
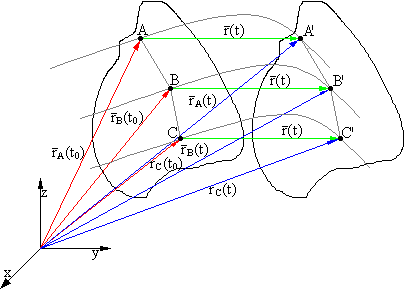
Równania ruchu poszczególnych punktów:
Prędkość punktów w ruchu postępowym, wektor prędkości:
![]()
Wektor przyspieszenia:
![]()
4. Ruch obrotowy ciała sztywnego
Jeżeli unieruchomimy dwa dowolne punkty bryły sztywnej, to wszystkie punkty leżące na prostej łączącej te dwa punkty (będące nieruchome, stanowiące oś obrotu) będą mogły poruszać się po okręgach w płaszczyznach prostopadłych do osi obrotu o środkach na niej leżących.
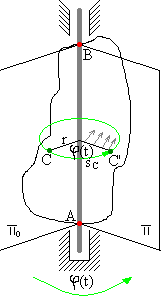
Tor każdego ciała poruszającego się ruchem obrotowym jest okręgiem leżącym w płaszczyźnie prostopadłej do osi obrotu o środku leżącym na tej osi i opisany jest promieniem o długości równej odległości punktu od osi obrotu. sC=φ(t)·r
Prędkość liniowa punktu:
WIELKOŚCI KĄTOWE (określają ruch całej bryły) |
WIELKOŚCI LINIOWE (dotyczą tylko określonego punktu ) |
|
|
|
|
|
|
![]()
Prędkość kątowa ω.
sc=φ(t)·r
![]()
![]()
![]()
Kierunek przyspieszenia normalnego równoległy do promienia CO, zwrot od C do O.
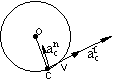
![]()
Kierunek przyspieszenia stycznego prostopadły do promienia, zwrot zgodny ze zwrotem ε.
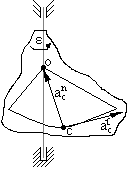
![]()
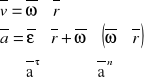
![]()
5. Ruch płaski ciała sztywnego; równania ruchu; metody wyznaczania prędkości i przyśpieszeń
To ruch w którym wszystkie punkty ciała poruszają się w płaszczyznach równoległych do płaszczyzny zwanej płaszczyzną kierującą.
Ruch płaski bryły sztywnej można przedstawić:
- jako przemieszczenie i obrót
- jako obrót wokół szczególnego punktu
Ruch płaski jako złożenie przemieszczenia i obrotu:
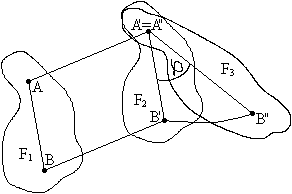
Równania:
xA=xA(t) xB=xB(t)
yA=yA(t) yB=yB(t)
Rych obrotowy:
![]()
Obrót wokół chwilowego środka obrotu:
Twierdzenie Eulera - dowolne przemieszczenie figury płaskiej w jej płaszczyźnie, może być dokonane za pomocą pewnego punktu zwanego środkiem obrotu. Wokół każdego środka, obrót trwa nieskończenie krótko, dlatego też punkty te nazywamy chwilowymi środkami obrotu.
Metody wyznaczania prędkości w ruchu płaskim:
- analityczna
- rzutów prędkości
- superpozycji
- chwilowego środka obrotu
- prostej przechodniej
- prędkości odwróconych
Metody wyznaczania przyspieszeń w ruchu płaskim:
- superpozycji
- chwilowego środka przyspieszeń
6. Ruch kulisty ciała sztywnego; prędkość i przyśpieszenie w ruchu kulistym
To taki ruch ciała sztywnego podczas którego jeden punkt zwany środkiem ruchu kulistego jest nieruchomy, zaś torami pozostałych punktów są powierzchnie kuli o środku w punkcie będącym środkiem ruchu kulistego.
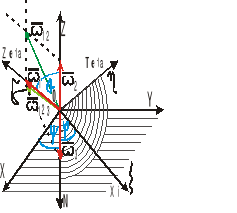
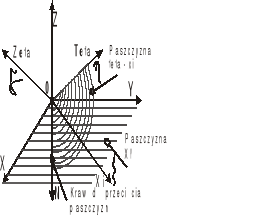
Ruch kulisty opisujemy przy pomocy kątów Eulera.
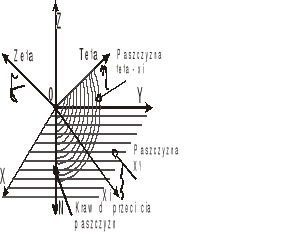
φ - kąt obrotu własnego
ψ - kąt precesji
![]()
-kąt nutacji
Kąty Eulera:
Podczas ruchu ciała sztywnego wartości kątów obrotu własnego, precesji, nutacji zmieniają się w czasie:
![]()
![]()
![]()
Aby jednocześnie określić ruch należy podać trzy równania. Ruch ciała sztywnego w ruchu kulistym ma trzy stopnie swobody.
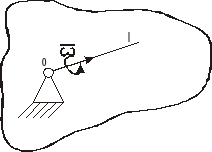
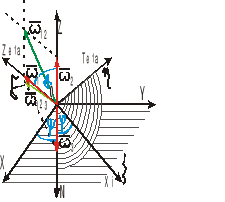
Prędkość kątowa w ruchu kulistym
![]()
- prędkość kątowa obrotu własnego
![]()
- prędkość kątowa precesji
![]()
- prędkość kątowa nutacji
Prędkość kątowa wyrażona jest jako suma geometryczna: ![]()
Prędkość dowolnego punktu w ruchu kulistym
![]()
Przyspieszenie w ruchu kulistym
![]()
![]()
![]()
stąd 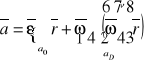
Precesja regularna: kąt nutacji jest stały, a prędkość nutacji równa się 0 - wartości prędkości obrotu własnego i precesji są stałe.
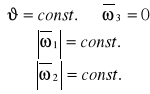
Prędkość kątowa precesji wynosi: ![]()
Suma geometryczna: ![]()
Przyspieszenie kątowe: ![]()
Wektor przyspieszenia kątowego ![]()
jest prostopadły do płaszczyzny wyznaczonej wektorami ![]()
oraz![]()
.
7. Ruch złożony
Ciało porusza się względem pewnego układu odniesienia, który to układ porusza się względem innego układu odniesienia.
- Wielkości kinematyczne to wielkości występujące w kinematyce: tor prędkości, przyspieszenie, droga.
- Wielkości kinematyczne bezwzględne to wielkości kinematyczne dotyczące poruszającego się pkt P odniesione do stałego układu odniesienia.
- Wielkości kinematyczne względne to wielkości kinematyczne dotyczące poruszającego się pkt P odniesione do ruchomego układu odniesienia.
- Wielkości kinematyczne unoszenia to wielkości kinematyczne przynależne temu pkt ruchomego układu odniesienia, który w danej chwili pokrywa się z pkt P. Inaczej mówiąc są to wielkości opisujące ruch układu ruchomego względem nieruchomego.
- Ruch pkt P w układzie stałym nazwiemy ruchem bezwzględnym.
- Ruchem pkt P w ruchomym układzie nazwiemy ruchem bezwzględnym.
- Ruchem układu ruchomego względem układu stałego nazwiemy ruchem unoszenia
DYNAMIKA
1. Dynamiczne równania ruchu punktu materialnego.
Badanie ruchu punktu materialnego o masie m i przyśpieszeniu a, na który działa siła F, sprowadza się do analizy drugiego prawa Newtona: Fa=m
Wektorowe równanie różniczkowe ruchu punktu materialnego:
![]()
![]()
![]()
2. Zasada d'Alemberta.
Suma sił rzeczywistych i siły bezwładności działających na punkt materialny jest w każdej chwili równa zeru.
![]()
Siłą bezwładności (siłą d'Alemberta) nazywamy fikcyjną siłę ![]()
równą co do wartości iloczynowi masy i przyspieszenia punktu materialnego lecz przeciwnie do tego przyspieszenia skierowana.
W układzie Kartezjańskim: ![]()
Z równania ![]()
wynikają następujące równania różniczkowe: ![]()
.
3. Pęd masy. Impuls siły. Kręt.
Pędem punktu materialnego o masie m i prędkości v nazywamy iloczyn masy punktu i jego prędkości: p = mv
Pęd jest wektorem o kierunku prędkości, a więc jest wektorem stycznym do toru punktu materialnego.
Impuls siły (popęd siły) wielkość charakteryzująca działanie wywierane na ciało przez siłę F(t) w ciągu pewnego czasu Δt=t2-t1, wynosząca 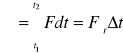
Krętem kO punktu materialnego o masie m względem punktu O nazywamy moment pędu vpm= tego punktu materialnego względem punktu O: ![]()
Jest wektorem prostopadłym do płaszczyzny wyznaczonej przez punkt O i wektor prędkości v
4. Praca mechaniczna
Pracą mechaniczną nazywamy energię dostarczoną z zewnątrz za pomocą układu sił do rozpatrywanego układu materialnego w czasie jego ruchu.
Pracą elementarną siły P na przesunięciu elementarnym ds, równym przyrostowi promienia wodzącego dr, nazywamy iloczyn skalarny siły P i przemieszczenia dr: dL=P.dr
5. Energia kinetyczna. Zasada równowartości pracy i energii kinetycznej.
Energią kinetyczną punktu materialnego o masie m, poruszającego się z prędkością v, nazywamy połowę iloczynu masy punktu i kwadratu jego prędkości: ![]()
Zasada równowartości pracy i energii kinetycznej
Przyrost energii kinetycznej układu punktów materialnych w skończonym przedziale czasu jest równy pracy wykonanej w tym samym czasie przez wszystkie siły zewnętrzne i wewnętrzne.
E2-E1=LZ+LW
Przyrost energii kinetycznej bryły sztywnej w skończonym przedziale czasu jest równy pracy wykonanej w tym samym czasie przez wszystkie siły zewnętrzne działające na tę bryłę.
E2-E1=LZ
6. Potencjalne pole sił. Energia potencjalna.
Widzimy, że praca wykonana przez siłę opisaną wzorem ![]()
![]()
![]()
na przemieszczeniu jej z położenia początkowego do końcowego jest równa ubytkowi funkcji U. Funkcję tę nazywamy potencjałem albo energią potencjalną, siłę P spełniającą powyższy warunek siłą potencjalną lub zachowawczą, a pole sił polem potencjalnym lub zachowawczym.
Potencjał w określonym punkcie przestrzeni jest równy pracy, którą wykonują siły potencjalne przy przemieszczaniu punktu materialnego z danego punktu do punktu, w którym potencjał jest równy zeru. Ponieważ punkt ten może być obrany dowolnie, potencjał jest określony z dokładnością do dowolnej stałej C.
Własności sił potencjalnych:
- Praca siły potencjalnej nie zależy od toru jej punktu przyłożenia, lecz jedynie od położenia tego punktu w chwilach początkowej i końcowej.
- Praca wykonana przez siłę potencjalną jest równa ubytkowi energii potencjalnej wynikającemu z przemieszczania się punktu przyłożenia siły. Wynika stąd również, że praca po torze zamkniętym jest równa zeru.
7. Zasada zachowania energii.
Gdy na układ materialny działają siły potencjalne, wtedy suma energii kinetycznej i potencjalnej tego układu jest wielkością stałą.
Układy materialne, do których odnosi się zasada zachowania energii mechanicznej, nazywamy układami zachowawczymi, a siły siłami zachowawczymi. Układy, których nie dotyczy ta zasada, nazywamy układami rozpraszającymi lub dyssy-patywnymi, np. układy z tarciem.
8. Zasada ruchu środka masy.
Środek masy układu materialnego porusza się tak jak punkt materialny o masie równej całkowitej masie układu, na który działa siła równa wektorowi głównemu sił zewnętrznych działających na ten układ. maC=W
Siły wewnętrzne nie mogą zmienić ruchu środka masy ani jego położenia.
9. Zasada pędu i zachowania pędu.
Zasada pędu punktów materialnych
![]()
Pochodna względem czasu pędu układu punktów materialnych jest równa wektorowi głównemu sił zewnętrznych działających na ten układ.
Prawo zmienności pędu (zasada pędu i popędu)
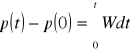
Przyrost pędu układu materialnego w skończonym przedziale czasu jest równy popędowi wektora głównego sił zewnętrznych działających na ten układ.
Zasada zachowania pędu
p=const
Jeżeli wektor główny układu sił zewnętrznych działających na układ materialny jest równy zeru, to pęd tego układu materialnego jest stały.
10. Zasada krętu i zachowania krętu.
Zasada krętu
![]()
Pochodna względem czasu krętu układu punktów materialnych względem dowolnego nieruchomego punktu jest równa momentowi głównemu wszystkich sił zewnętrznych względem tego samego punktu.
Zasada zachowania krętu
kO(t)-kO(0)=0 czyli kO(t)=kO(0)=const lub jeżeli MO=0 to kO=const
Jeżeli moment główny sił zewnętrznych względem nieruchomego punktu redukcji O jest równy zeru, to kręt układu materialnego (bryły) względem tego punktu jest wielkością stałą.
11. Momenty bezwładności
Momentem bezwładności punktu materialnego względem bieguna (punktu), płaszczyzny lub osi nazywamy iloczyn masy tego punktu i kwadratu jego odległości od bieguna, płaszczyzny lub osi.
Rodzaje momentów bezwładności:
- biegunowe (momenty bezwładności względem punktu)
- względem płaszczyzn
- względem osi (osiowe momenty bezwładności)
Momenty bezwładności układu punktów materialnych
Biegunowym momentem bezwładności IO układu punktów materialnych względem punktu O nazywamy sumę iloczynów mas mk i kwadratów ich odległości rk2 od punktu O, czyli ![]()
Momentami bezwładności Ixy, Iyz, Izx względem płaszczyzn xy, yz, zx układu punktów materialnych nazywamy sumy iloczynów mas mk przez kwadraty ich odległości od tych płaszczyzn. ![]()
![]()
![]()
Momentami bezwładności Ix, Iy, Iz względem osi x, y, z układu punktów materialnych nazywamy sumy iloczynów mas mk oraz kwadratów ich odległości od tych osi:
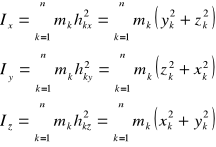
Momenty dewiacyjne
Momentami dewiacyjnymi Dxy, Dyz, Dzx układu punktów materialnych nazywamy sumę iloczynów mas mk przez iloczyn ich odległości od dwóch prostopadłych płaszczyzn yz i zx, zy i xy, xy i yz. Momenty te wyrażają wzory:
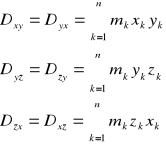
Momenty dewiacyjne mogą przyjmować wartości zarówno dodatnie, jak i ujemne, ponieważ w powyższych wzorach − w przeciwieństwie do momentów bezwładności − występują iloczyny, a nie kwadraty współrzędnych. Jeżeli układ materialny ma dwie płaszczyzny symetrii, to wszystkie momenty dewiacyjne będą równe zeru.
Momenty bezwładności bryły
Biegunowy moment bezwładności jest równy sumie momentów bezwładności względem trzech prostopadłych płaszczyzn przechodzących przez ten biegun: IO=Iyz+Izx+Ixy
Zależności na momenty bezwładności względem osi mają postać:
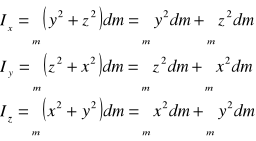
Moment bezwładności względem osi jest równy sumie momentów bezwładności względem dwóch prostopadłych płaszczyzn przecinających się wzdłuż tej osi. Ix=Izx+Ixy Iy=Ixy+Iyz Iz=Iyz+Izx
Biegunowy moment bezwładności jest równy połowie sumy momentów bezwładności względem trzech prostopadłych osi przechodzących przez ten biegun. ![]()
12. Energia kinetyczna w ruchu postępowym i obrotowym.
Energia kinetyczna ciała w ruchu postępowym
W ruchu postępowym ciała sztywnego prędkości wszystkich jego punktów w każdej chwili są geometrycznie równe.
![]()
Energia kinetyczna ciała w ruchu postępowym jest równa połowie iloczynu masy ciała i kwadratu jego prędkości.
Energia kinetyczna ciała w ruchu obrotowym
![]()
Energia kinetyczna ciała w ruchu obrotowym jest równa połowie iloczynu momentu bezwładności ciała względem osi obrotu i kwadratu prędkości kątowej ciała.
13. Twierdzenie Koeniga.
Energia kinetyczna układu punktów materialnych jest równa energii tegoż układu w jego ruchu względem środka masy oraz energii kinetycznej masy całkowitej poruszającej się z prędkością środka masy.
![]()
Energia kinetyczna bryły w ruchu ogólnym jest sumą energii kinetycznej bryły w jej chwilowym ruchu obrotowym względem środka masy i energii kinetycznej masy całkowitej poruszającej się z prędkością środka masy.
14. Dynamika ciała sztywnego - ruch postępowy, obrotowy i płaski
Ruch postępowy
Aby ciało sztywne mogło się poruszać ruchem postępowym, suma geometryczna momentów względem środka masy sił zewnętrznych działających na to ciało nie musi być równa zeru.
![]()
![]()
![]()
Ruch obrotowy
![]()
Jeżeli ![]()
to ![]()
ciało porusza się ruchem przyspieszonym
Jeżeli ![]()
to ![]()
ciało porusza się ruchem jednostajnym
Jeżeli ![]()
to ![]()
ciało porusza się ruchem opóźnionym
Ruch płaski
W kinematyce ruchu bryły sztywnej ruchem płaskim nazywamy ruch, w czasie którego wszystkie punkty bryły zakreślają tory równoległe do pewnej płaszczyzny nazywanej płaszczyzną ruchu lub płaszczyzną kierującą.
- oś z′ jest główną centralną osią bezwładności
- ruch bryły odbywa się pod wpływem sił działających w płaszczyźnie ruchu
![]()
![]()
![]()
15. Wahadło fizyczne i matematyczne
Wahadło fizyczne
Ciało materialne, które może się swobodnie obracać dookoła poziomej osi.
Wzór na okres drgań wahadła fizycznego dla małych wychyleń:
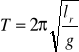
wprowadzając wielkość długość zredukowana wahadła lr
![]()
gdzie:
d - odległość od punktu zawieszenia do środka ciężkości,
g - przyspieszenie ziemskie,
I - moment bezwładności ciała względem osi obrotu,
m - masa ciała
Dzięki wahadłu fizycznemu można wyznaczać momenty bezwładności brył.
Wahadło matematyczne
Punkt materialny zawieszony na nierozciągliwej i nieważkiej nici. Jest to idealizacja wahadła fizycznego.
Ważną cechą wahadła fizycznego i matematycznego jest stałość okresu drgań dla niewielkich wychyleń wahadła.
16. Reakcje dynamiczne łożysk osi obrotu
MO. ω=MOx' ωx'+ MOy' ωy'+ MOz' ωz'=0
Reakcje dynamiczne występują tylko w czasie ruchu ciała sztywnego, tzn. gdy ω≠0
Jeżeli oś obrotu bryły jest główną centralną osią bezwładności, czyli bryła jest wyważona statycznie i dynamicznie, to reakcje dynamiczne są równe zeru.
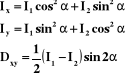
Wzory pomocne przy obliczaniu reakcji dynamicznych
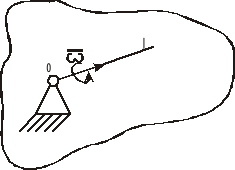
17. Oś swobodna
To oś przechodząca przez środek masy i taka, że wypadkowa sił odśrodkowych i ich momentów działających na ciało wynosi zero.
Na ogół ustabilizowany obrót ciała odbywa się wokół tej osi symetrii, której odpowiada największy moment bezwładności. Swobodna oś obrotu nie wymaga łożysk.
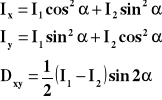
Wyszukiwarka
Podobne podstrony:
Statyka egzamin statyka ściąga, pojęci a-1
statyka egzamin - pytania 1 termin, Inżynieria Środowiska, 5 semestr, Statyka budowli, wykład
pytania z egzaminu ze statyki z zeszłego roku
statyka egzamin
Egzamin zaoczne
Pytania egzaminacyjneIM
ANALIZA WYNIKÓW EGZAMINU GIMNAZJALNEGO DLA UCZNIÓW KLAS III
zadania egzaminacyjne
4 Statyka Kinetyka
Egzamin 2008 2009
więcej podobnych podstron