1.Opis teoretyczny :

Teorii kinetyczno-molekularnej zawdzięczamy specjalne, "mikroskopowe" ujęcie zjawisk zachodzących w otaczającym nas świecie . Teoria ta opiera się na następujących założeniach ogólnych :

ciała mają budowę nieciągłą , składają się z drobnych elementów w postaci atomów lub cząsteczek (molekuł)

cząsteczki gazu znajdują się w szybkim nieustannym , chaotycznym ruchu, poruszają się we wszystkich możliwych kierunkach, przy czym żaden z tych kierunków nie jest wyróżniony

pomiędzy poszczególnymi cząsteczkami występują siły wzajemnego oddziaływania

cząsteczki doznają zderzeń sprężystych między sobą i ścianami naczynia w których się znajdują ,

czas trwania zderzenia jest znacznie krótszy od czasu , który upływa między zderzeniami .

między zderzeniami cząsteczki poruszają się po liniach prostych

Oddziaływania międzycząsteczkowe w dużym stopniu zależą od wzajemnych

odległości między cząsteczkami i gwałtownie maleją ze wzrostem tych odległości,

dlatego dzięki stosunkowo dużym średnim odległościom międzycząsteczkowym

można w pierwszym przybliżeniu zaniedbać siły wzajemnego oddziaływania

cząsteczek .Dzięki temu można założyć, że każda cząsteczka gazu porusza się

swobodnie ( bez działania sił ) aż do momentu zderzenia z inną cząsteczką lub ze

ścianką naczynia .Stąd wniosek , że odcinki dróg między kolejnymi zderzeniami są

przebywane ruchem jednostajnym prostoliniowym . Wobec zupełnej przypadkowości

zderzeń drogi te mają różne długości

Cząsteczki podczas zderzeń zmieniają swe prędkości. Zderzenia cząsteczek

gazowych można traktować jako zderzenia doskonale sprężyste , a średnia długość

prostoliniowego przebiegu między dwoma zderzeniami , wyliczona z bardzo wielkiej

liczby tych przelotów, nosi nazwę średniej drogi swobodnej . Jej wartość dla tlenu w

warunkach normalnych wynosi 6,4·10-8 m . Wyznaczono też średnie prędkości ruchu

cząsteczek . Dla tlenu w temperaturze 0C wynosi 425 m/s.

Wyróżniamy następujące przemiany gazowe :

1. Przemiana izotermiczna - zachodzi w stałej temperaturze ( T = const )Do przemiany

tej odnosi się prawo Boyle'a - Mariotte'a.

p1· V1/T = p2 · V2 /T / T

p1· V1 = p2· V2

czyli

p· V = const.

W przemianie izotermicznej ciśnienie jest odwrotnie proporcjonalne do objętości.

W stałej temperaturze średnia energia kinetyczna cząsteczek jest niezmienna . Jeśli

masa jest określona , to liczba cząsteczek N zawartych w tej masie jest stała

p· V = 2/3N· m2/2

Jeśli zrobimy wykres izotermy p = f(V) , otrzymamy gałąź hiperboli równobocznej.

Przy przemianie izotermicznej gaz rozszerzając się wykonuje pracę .

Ponieważ energia wewnętrzna gazu przy tej przemianie jest stała , z pierwszego prawa termodynamiki wynika , że gaz może wykonywać izotermiczne pracę tylko kosztem dostarczonego z zewnątrz ciepła . Praca wykonana przez gaz przy rozprężaniu jest równa

W = pV

Stosując rachunek całkowy , pracę tę możemy wyrazić dokładniej wzorem :

W = pdV

Z równania gazów doskonałych

p = RT/V

gdzie R - stała gazowa

a zatem

W =RTdV/V = RT ( ln V2- lnV1)

stąd ostatecznie

W = RT ln(V2/V1)

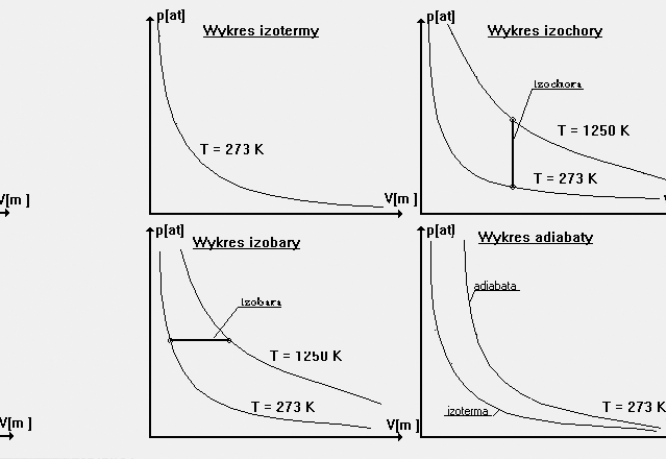
2. Przemiana izochoryczna- zachodzi przy stałej objętości (V = const ).Realizujemy

ją gdy w zamkniętym pomieszczeniu znajduje się gaz który oziębiamy lub ogrzewamy.

Z równania stanu gazu doskonałego wynika że dla przemiany izochorycznej

p/T = const

czyli ciśnienie jest wprost proporcjonalne do temperatury bezwzględnej gazu .

Wykresem p = f(V) tej przemiany jest odcinek równoległy do osi rzędnych .Przy

przemianie tej gaz nie wykonuje pracy na zewnątrz , natomiast rośnie jego energia

wewnętrzna w związku ze zmianą temperatury.

3. Przemiana izobaryczna - zachodzi przy stałym ciśnieniu (p = const).

Z równania gazów doskonałych wynika , że pod stałym ciśnieniem

V/T = const

czyli objętość jest wprost proporcjonalna do temperatury w K. Na wykresie p = f( V )

izobarę przedstawia odcinek równoległy do osi odciętych . Przy przemianie

izobarycznej gaz rozprężając się wykona pracę

W = p(V2 - V1)

gdyż V2 - V1 oznacza przyrost objętości.

4. Przemiana adiabatyczna - zachodzi bez wymiany ciepła z otoczeniem .

Q = 0 , Q = const

Ponieważ dla jednego mola gazu doskonałego

U = CVT

mamy dla przemiany adiabatycznej na podstawie pierwszej zasady termodynamiki

CVT = -pV

gdzie CV - ciepło molowe przy stałej objętości .

Na podstawie równania Clapeyrona , ciśnienie p wyrażone jest wzorem

p = RT/V ,

a zatem mamy:

CVT+RT/VV = 0

dzieląc przez T znajdziemy stąd

CVT/T+R V/ v = 0

Przechodząc do różniczek możemy związek ten napisać w postaci

CVdT/T+R dV/ v = 0

zaś ostatni związek możemy od razu scałkować korzystając z tego , że dT/T jest

pochodną lnT , zaś dV/V pochodną lnV . A zatem po scałkowaniu mamy

CVlnT+RlnV = const

R = Cp-CV

gdzie Cp -ciepło molowe przy stałym ciśnieniu.

Ten związek przybierze postać

TCvV Cp-CV = const

ciągniemy jeszcze z obu stron pierwiastki stopnia CV ,znajdziemy wtedy

TV(Cp-CV)/Cv= const

wprowadzimy oznaczenie

= Cp/CV

związek TV(Cp-CV)/Cv= const możemy napisać w postaci

TV-1 =const

z równania gazu doskonałego

T = pV/R

ostatecznie otrzymujemy równanie adiabaty w postaci :

p· V = const

Wykres p = f(V) adiabaty przebiega bardziej stromo niż izotermy .

Oprócz wymienionego wyżej prawa Boyle'a - Mariotte'a przemiany gazowe opisują

jeszcze prawa : Avogadra i Daltona . Prawo Avogadra mówi , że w jednakowych

objętościach różnych gazów mierzonych pod tym samym ciśnieniem i w tej samej

temperaturze znajduje się jednakowa liczba cząsteczek

N1 = N2

Prawo Daltona mówi zaś , że ciśnienie jest równe sumie ciśnień cząstkowych p1,

p2,p3, .... jakie wywierają poszczególne gazy wchodzące w skład mieszaniny zajmując

każdy z osobna całą objętość V :

p = p1+p2+p3+.....

Ciepło właściwe dowolnego ciała wyraża się liczbowo jako ilość ciepła potrzebna do

ogrzania 1 kg ciała o 1 deg ( 1C lub 1K ) . Jednostką ciepła właściwego , jest:

J/(KG· deg)

Ciepło właściwe jest nie tylko funkcją temperatury , zależy ono także od tego czy

ogrzewanie ciała odbywa się z zachowaniem stałej objętości , czy też pod stałym

ciśnieniem . Podczas ogrzewania ciała z zachowaniem stałej objętości ciepło musi być

dostarczone jedynie na wykonanie przyrostu energii wewn. związanego ze wzrostem

temperatury , natomiast podczas ogrzewania pod stałym ciśnieniem ciało rozszerza się

i pokonuje opór wynikający z istnienia zewnętrznego ciśnienia , a zatem wykonuje

pracę . W tym przypadku ciepło zużywane jesz na zwiększenie energii wewnętrznej

ciała oraz na wykonanie pracy związanej ze zmianą objętości . Ciepło właściwe pod

stałym ciśnieniem Cp jest większe od ciepła właściwego stałej objętości Cv .Często

posługujemy się ciepłem molowym zdefiniowanym jako ilość ciepła , które należy

dostarczyć 1 molowi ciała , aby podnieść jego temperaturę o 1C. Między ciepłem

molowym C , a ciepłem właściwym istnieje związek C = C gdzie - masa drobinowa

danego ciała .

Przy ogrzewaniu pod stałym ciśnieniem

Cp - Cv = R R - stała gazowa

Cp = Cv+R = {(i+2)/2}· R i - ilość stopni swobody

Biorąc pod uwagę oba równania mamy :

= Cp/Cv = (i+2)/2 - dla danego gazu jest wielkością stałą

Przez liczbę stopni swobody drobin rozumiemy liczbę niezależnych współrzędnych

koniecznych do opisania jej ruchu . Drobiny gazu mogą wykonywać tylko ruchy

postępowe ( gaz jednoatomowy ) . Opisanie tego ruchu wymaga 3 współrzednych .

Drobiny gazu dwu i wieloatomowych mogą wykonywać także ruchy rotacyjne oraz

oscylacyjne . W przypadku gazów dwuatomowych i = 5 ( 3 współrzędne ruchu

postępowego + 2 rotacyjne - dookoła dwóch wzajemnie prostopadłych osi ).

Uwzględnienie możliwości oscylacji zwiększa liczbę stopni swobody do 7 ( 2

dodatkowe współrzędne do opisania energii kinetycznej drgań oraz wzajemnej energii

potencjalnej atomów ) . W myśl prawa ekwipartycji energii na każdy stopień swobody

przypada średnio ta sama ilość energii . Energia wew. gazu doskonałego jest suma

energii kinetycznej ruchu cieplnego wszystkich cząsteczek gazu , znajdujących się

w danej objętości:

U = N· f kT/ 2 = f RT/2 N- liczba Avogadro

f- liczba stanów swobody

Jeśli 1kmol ogrzewamy w stałej objętości przy czym przyrost temp = dT , to

doprowadzone ciepło dQ = CvdT , ponieważ gaz nie zmienia objętości , czyli nie

wykona pracy dW = 0 więc dQ = dU = CvdT

U = f R/2 T = Cv T Cv = fR/2

Przypuśćmy , że w zbiorniku mamy 1 kmol gazu . Ciepło dQ potrzebne do ogrzania o dT:

dQ = Cp

dQ+ dW = dU lub CpdT- pdV= CvdT

pV = RT - różniczkując dla procesu izobarycznego p = const

pdV = RdT podstawiając CpdT- RdT = CvdT /:dT

Cp-Cv = R

Zgodnie z poprzednim

Cv = fR/2 = dU/dT więc

Cp = Cv+R = fR/2 + R = R (f+2)/2 a = Cp/Cv = (f+2)/f

Metoda doświadczalna znajdowania .

W dużym naczyniu szklanym N o objętości kilkudziesięciu litrów zawarty jest

badany gaz , znajdujący się pod ciśnieniem p niewiele wyższym od ciśnienia

atmosferycznego . Gaz zamknięty jest kurkiem , który w pewnej chwili otwieramy i

zamykamy ponownie z chwilą wyrównania się ciśnienia z ciśnieniem atmosferycznym .

Powietrze rozpręża się , przy czym można przyjąć , że rozprężenie to zachodzi

adiabatycznie , ulega ono przy tym oziębieniu .

Po pewnym czasie dzięki wymianie z otoczeniem temperatura powietrza pozostałego

w naczyniu zrówna się w temp. otoczenia i wskutek ogrzania ciśnienie gazu podniesie

się , wytworzy się więc nadwyżka ciśnienia , tym razem mniejsza od nadwyżki

początkowej.

Niech początkowa nadwyżka = p1 , wypuszczenie gazu na zewnątrz odpowiada

rozprężeniu o V , rozprężeniu temu odpowiada spadek ciśnienia

(-p) q = p1

Przypuśćmy , że po wyrównaniu się temperatur nadwyżka ciśnienia wynosi p2 .

W porównaniu z ciśnieniem początkowym nastąpił spadek o p1-p2 , ale ten sam

spadek otrzymaliśmy rozprężając gaz izotermicznie o tę samą V zatem (-p) T = p1-p2 ze wzoru na adiabatę

(p) q/V = - p/V

z izotermy

(p) T/T = - p/V

porównując stronami znajdujemy

= (p) q/ (p) T

Ponieważ w obu przypadkach mamy te same wartości p i V to:

= p1/(p1-p2) = h1/(h1-h2)

2.Układ pomiarowy.

3. Tabela pomiarowa.

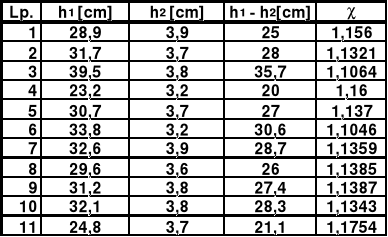
4.Opracowanie wyników

Na podstawie otrzymanych wyników obliczamy stosunek Cp/Cv ze wzoru:

= Cp/Cv = h1/(h1-h2)

Np. dla pomiaru pierwszego otrzymujemy:

= 28,9/(28,9 - 3,9) = 1,156

Wartość średnia tego stosunku dla wszystkich pomiarów wynosi:

= 1/n· i = 1,1381

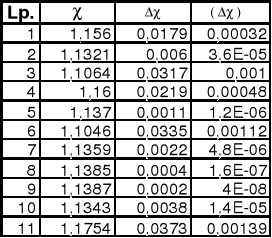
Błędy pomiarowe obliczamy metodą Gaussa.

obliczamy błędy poszczególnych pomiarów ( wyniki w tabeli ) ze wzoru:

i = - i

Dla pierwszego pomiaru mamy:

i = 1,1381 - 1,156 =0,0179

obliczamy sumę kwadratów błędów poszczególnych pomiarów

( i )2 = 0,0043

obliczamy średni błąd kwadratowy wartości średniej

= ( i )2/n· (n-1)

= 0,0043/ 11· (11-1) = 0,0062

Ostateczny wynik stosunku Cp/Cv podajemy w postaci:

=

czyli:

= 1,1381 0,0062

Jest to najbardziej prawdopodobny wynik serii pomiarów.

5. Uwagi i spostrzeżenia.

Błąd w głównej mierze spowodowany jest mylnymi odczytami wysokości słupa

wody oraz nieszczelnością układu pomiarowego ( w założeniu przemiana adiabatyczna zachodzi bez wymiany ciepła z otoczeniem ).

Niepewność odczytu wynika ze skończonej wartości grubości podziałki na przyrządzie pomiarowym ( miara krawiecka ) oraz przyciąganie między cząsteczkowym , które powoduje powstawanie na powierzchni cieczy . Niemożliwe więc było jednoznaczne ( w każdym z 11 pomiarów ) określenie wysokości słupa wody co spowodowało powstanie odchyłek w przeprowadzonych pomiarach .

Porównanie otrzymanego wyniku z wartością tablicową.

Cząstki jednoatomowe mają trzy stopnie swobody , odpowiadające trzem wzajemnie prostopadłym translacjom x,y,z , a więc dla gazów a więc dla gazów jednoatomowych :

= 5/3 = 1,67

Cząstki dwuatomowe mogą ponadto wykonywać obroty wokół dwóch wzajemnie prostopadłych osi i drgania łączącej oba atomy . Czyli mają 6 stopni swobody ( 3 translacje , 2 rotacyjne i 1 oscylacyjny ) . A zatem dla gazów dwuatomowych przy załorzeniu . że cząstki nie wykonują oscylacji :

= 7/5 = 1,4

Załorzenie powyższe jest uzasadnione , ponieważ w temperaturach pokojowych ruchy oscylacyjne dla większości lekkich cząstek dwuatomowych są całkowicie "zamrożone" . Uruchomienie iscylacji w wyższych temperaturach powoduje obniżenie wartości , natomiast zamrożenie ruchów rotacyjnych cząstki występującej w niższych temperaturach prowadzi do wzrostu wartości

Ponieważ powietrze z większości składa się z tlenu i azotu można przyjąć że wartość dla powietrza wynosi 1,4 .

Natomiast dla powietrza wyznaczone doświadczalnie wynosi :

1,13810,0062

W rzeczywistości otrzymana doświadczalnie wartość jest różna od przewidywań teorii . Wynika to z wielu uproszczeń występującyh w tej klasycznej metodzie kinetyczno - cząstkowej teorii. Jak wiadomo teoria ta nie uwzględnia rotacyjnych stopni swobody atomów w cząsteczce . Nie uwzględnia także elektronowych ijądrowych stopni swobody w atomie . Wpływ może mieć także fakt że powietrze oprócz azotu itlenu składa się dodatkowo z 1%innych gazów .

---