Politechnika Częstochowska

Katedra Fizyki

Ćwiczenie nr 10

Temat: Wyznaczanie współczynnika

przewodnictwa temperaturowego

ciał stałych.

Ćwiczenie wykonali:

Sergiusz Jowsa

Marcin Rokoszewski

Wprowadzenie teoretyczne.

1.Makroskopowy opis przewodnictwa cieplnego.

Ciało stałe posiadające różne temperatury w różnych punktach, odizolowane od wpływu otoczenia dąży do wyrównania temperatur, zgodnie z drugą zasadą termodynamiki. Szybkość wyrównywania się temperatur zależy od ich różnicy i rodzaju ciała. Każde ciało charakteryzuje tzw. współczynnik przewodnictwa temperaturowego zwany też współczynnikiem dyfuzji cieplnej. Wyrównywanie się temperatur spowodowane jest przepływem ciepła z obszarów o wyższej temperaturze do obszaru o temperaturze niższej. Zdolność przewodzenia ciepła przez ciało charakteryzuje współczynnik przewodnictwa cieplnego ().

Oba powyższe współczynniki powiązane są prostą relacją:

gdzie: - gęstość ciała; c-ciepło właściwe ciała.

2.Mikroskopowy mechanizm przewodnictwa cieplnego.

2.1.Dielektryki

W mechanice kwantowej ruch cząsteczek wiąże się z rozchodzeniem fal. I przeciwnie rozchodzenie się fal w dowolnym ośrodku można powiązać formalnie z ruchem pewnego zbioru cząstek. W tym sensie można falom sprężystym związanym z drganiami atomów sieci przypisać zbiór cząstek zwanych fononami, których energia wynosi () zaś pęd (k). W temperaturze zera bezwzględnego fonony nie istnieją, zaś ze wzrostem temperatury liczba ich rośnie. W temperaturze wysokiej liczba ta jest proporcjonalna do temperatury T, a w temperaturach niższych od 0 /temp. Deday'a / jest proporcjonalna do T³.Z fizyki statystycznej wiadomo, że przewodnictwo cieplne gazu wyraża się wzorem ; przenieśmy ten wzór na gaz fononowy, wtedy (c)-będzie ciepłem właściwym substancji, (l)-średnią drogą fononów pomiędzy dwoma zderzeniami, (u)-prędkością dźwięku /czyli fononu /. Średnia droga swobodna będzie zależała od liczby fononów. Liczba fononów przy T<0 rośnie z temperaturą proporcjonalnie do T³, a dla T>0 już tylko jak T. Droga swobodna, a nią przewodnictwo cieplne zachowują się odwrotnie. Dla T<0 maleje dość szybko, dla T>0 maleje nadal, lecz wolniej - tak jak T^-1. W bardzo niskich temperaturach gdy droga swobodna fononów osiąga rozmiary kryształu przestaje ona wpływać na przewodnictwo cieplne. Wtedy przewodnictwo cieplne zależy tylko od ciepła właściwego, które w niskich temperaturach maleje do zera tak jak T³, a w wysokich jest niezależna od temperatury.

2.2.Metale.

Metale różnią się od dielektryków tym, że oprócz gazu fononowego nośnikami ciepła są elektrony swobodne tworzące tzw. gaz elektronowy. Elektrony tak wydatnie pomagają fononom w przewodzeniu ciepła, że przewodnictwo cieplne metali jest większe średnio 100 razy w porównaniu z przewodnictwem cieplnym dielektryków /pozbawionych swobodnych elektronów /.W temperaturze wyższej przewodzą ciepło prawie wyłącznie elektrony, udział fononów jest do pominięcia. Przewodnictwo w tym zakresie jest stałe ponieważ wzrost energii przenoszonej przez elektrony o wyższej temperaturze jest kompensowany zmniejszeniem się średniej drogi swobodnej. Półprzewodniki o bardzo małej koncentracji elektronów w paśmie przewodnictwa mają przewodnictwo cieplne podobne do przewodnictwa izolatorów, natomiast półprzewodniki o dużej ilości elektronów w paśmie przewodnictwa są bliższe pod tym względem metalom.

2.3.Szkła, ciała amorficzne i polikrystaliczne.

Całkiem odmiennie zmienia się z temperaturą przewodnictwo cieplne w ciałach polikrystalicznych, w których krystality są małe w porównaniu z średnią drogą swobodną fononów, a także w ciałach amorficznych, które można traktować jak ciała polikrystaliczne z krystalitami o rozmiarach atomów. W ciałach takich przewodnictwo cieplne w bardzo niskich temperaturach powinno rosnąć z temperaturą tak jak ciepło właściwe / ∼ T³ /, a następnie ponieważ ani (c), ani (l) nie zależą od temp. przewodnictwo cieplne pozostaje stałe.

3.Pomiar temperatury za pomocą termopary.

Termoparę, czyli termoogniwo stanowią dwa kawałki drutu albo prętów z różnych metali, spojone ze sobą na końcach. Jeżeli końce te znajdą się w różnych temperaturach, t₁ i t₂ , np. wskutek ogrzania jednego ze spojeń płomieniem palnika, to w obwodzie takim zaczyna płynąć prąd elektryczny. Kierunek prądu zależy od tego, które ze spojeń ma temperaturę wyższą.

TABELA 1

Lp.	Temperatura [^0C]	Temperatura [K]	STEM [dz]	STEM [mV]
1	20.5	293.5	0	0
2	22	295	2	0.06
3	24	297	6	0.18
4	26	299	10	0.3
5	28	301	12.5	0.375
6	30	303	15	0.45
7	32	305	17.5	0.525
8	34	307	22	0.66
9	36	309	24.5	0.735
10	38	311	28	0.84
11	40	313	31.5	0.945
12	42	315	35	1.05
13	44	317	39	1.17
14	46	319	43	1.29
15	48	321	46.5	1.395

TABELA 2

Lp.	STEM [dz]	STEM [mV]	DT=TO-TP [K]	Czas [s]	lnDT
1	48.5	1.455	31.9	0	3.46
2	47.5	1.425	31.2	180	3.44
3	45	1.35	29.6	360	3.39
4	40	1.2	26.3	540	3.27
5	34.5	1.035	22.7	720	3.12
6	29	0.87	19.1	900	2.95
7	22	0.66	14.5	1080	2.67
8	19.5	0.585	12.8	1260	2.55
9	16	0.48	10.5	1440	2.35
10	13	0.39	8.5	1620	2.15
11	11	0.33	7.2	1800	1.98
12	10.5	0.315	6.9	1980	1.93
13	8.5	0.255	5.6	2160	1.72
14	6.5	0.195	4.3	2340	1.45
15	5	0.15	3.3	2520	1.19
16	4	0.12	2.6	2700	0.97

Cechowanie termopary STEM=f(T)

03 [mV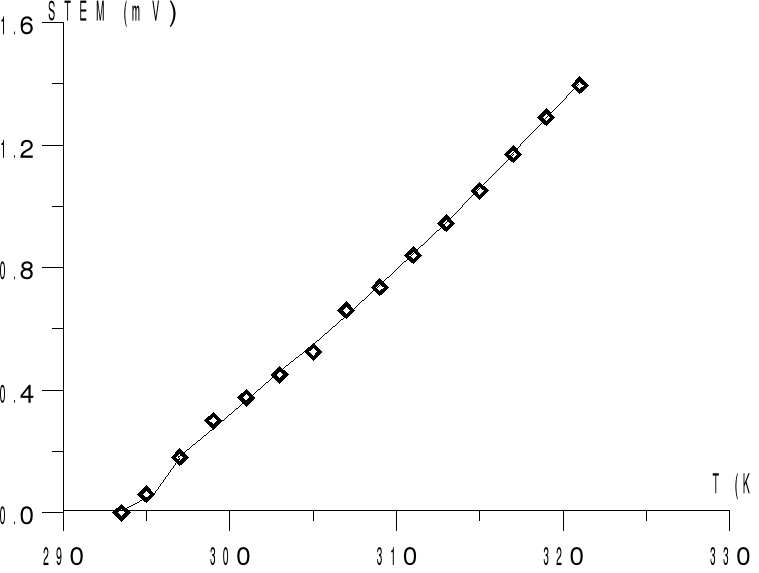

Wyznaczanie współczynnika K lnDT=f(t)

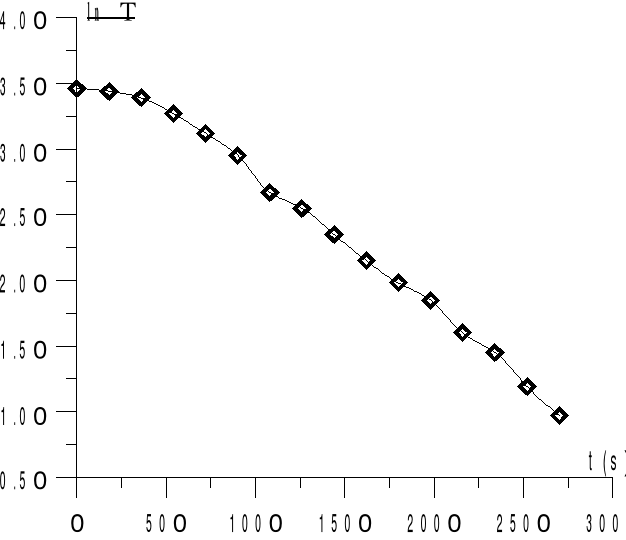
Przykładowe obliczenia.

Siła termoelektryczna STEM.

1. STEM [mV]=0.03 [mV/dz]* STEM[dz]

1. np. STEM [mV]=0.03*6=0.18 [mV]

Współczynnik temperaturowy napięcia termopary.

a_T=STEM_max - STEM_min/(T_K-T_P)

a_T=(1.395 - 0.3)/ (321 - 297)= 1.095/ 24 =45.63 * 10^-6 [V/K]

Różnica temperatur.

DT=T_O - T_P E_T =a_T*(T_O -T_P)= a_T*DT DT=E_T / a_T

np. DT= 1.35 [mV]/ 45.63 * 10^-6 [V/K]=29.6 [K] lnDT=3.39

Współczynnik przewodnictwa temperaturowego plexiglasu.

z pomiarów

tga= K*l_m.,n,l K=tga / l_m.,n,l = 4.9 *10^-8

z tablic

parametry plexiglasu: = 0.193 [W/ m. K]

r= 1190 [kg/ m³]

C_W= 1380 [I/ kg K]

[m²/s]

Wnioski.

Ćwiczenie polegało na wyznaczeniu współczynnika przewodnictwa temperaturowego ciała stałego, jakim był plexiglas. W tym celu w pierwszej części należało przeprowadzić cechowanie termopary, dzięki czemu znając różnicę temperatur DT=T_O -T_P można wyznaczyć charakterystykę lnDT=f(t), z której następnie można odczytać tangens kąta nachylenia prostoliniowej części charakterystyki. Obliczając l_m.,n,l łatwo można wyznaczyć współczynnik przewodnictwa temperaturowego ze wzoru, tga=K*l_m.,n,l . Dość duży błąd wyznaczonego współczynnika K wynika z kilku przyczyn. Jedną z nich był niedokładny pomiar czasu, błąd jednak nie był zbyt duży, gdyż czas był mierzony z dokładnością co do sekundy, co przy 42 minutach trwania pomiarów nie wprowadza większego błędu. Większy błąd wynika z niedokładnego odczytu STEM na galwanometrze w określonym czasie. Dodatkowym błędem jest nie dość dokładne wyznaczenie tangensa kąta nachylenia, ponieważ niewielkie odstępstwa w przyjęciu prostoliniowego odcinka wprowadzają duże różnice wartości tangensa kąta.

---