Zad.1
Przez ile miesięcy z kapitału równego 20 tys. zł może być wypłacana renta stała w wysokości 2 tys. zł miesięcznie z dołu, przy założeniu miesięcznej kapitalizacji zarówno renty jak i kapitału? Miesięczna stopa procentowa wynosi 1%.
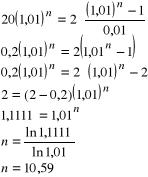
Odp. Przez 10,6 miesięcy.
Zad.2
Zwycięzca teleturnieju ma do wyboru cztery formy odebrania nagrody:
dostaje od razu 10000 zł
dostaje od razu 5000 zł, a po dwóch latach dostaje 7000 zł
będzie dostawał co roku przez 5 lat z góry 2500 zł (pierwsza płatność od razu)
będzie dostawał 1500 zł co roku z dołu do końca życia
Która forma nagrody jest najkorzystniejsza dla zwycięzcy teleturnieju? Roczna stopa procentowa 20%.
Porównywać można wyłącznie wartości tych nagród sprowadzone do tego samego momentu w czasie, np.:
na chwilę obecną. Liczymy wtedy Present Value każdej formy nagrody:
Ad. a) PV=10000
![]()
Ad. b) PV=5 + 7(1,2)-2 = 9861,11
Ad. c)
Ad. d) Tu nie da się policzyć PV, bo nie wiemy, ile ta osoba ma żywota przed sobą. Policzmy, ile musiałaby żyć, aby PV z tych corocznych wypłat po 1500 było równe 10000.
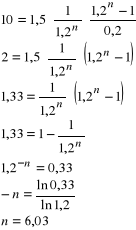
Aby PV corocznych płatności po 1500 zł każda była równa tej z podpunktu a), klient musiałby żyć jeszcze co najmniej 6,03 lat. Nie wiadomo, czy klient jest młody czy stary. Według mnie powinno się wybrać odp. a).
Zad. 3
Jaka jest efektywna stopa oprocentowania lokat, jeżeli kwartalna stopa nominalna wynosi 5%, a kapitalizacja jest roczna?
![]()
Zad.4 (?)
Zad.5 (?)
Zad.6 (?)
Zad.7
Jaka jest wartość wewnętrzna akcji, jeżeli spółka w zeszłym roku wypłaciła dywidendę w wysokości 50 zł i zamierza co roku zwiększać wysokość dywidendy o 2%? Rynkowa stopa zwrotu wynosi 0,22.
![]()
Zad. 8
Bank A udziela kredytów przy nominalnej rocznej stopie procentowej 22% przy kapitalizacji ciągłej, a Bank B udziela kredytów przy kapitalizacji miesięcznej z roczną stopą procentową 22,5%. Który bank posiada lepszą ofertę?
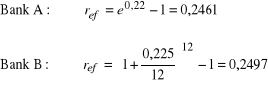
Odp.: Lepszą ofertą dysponuje Bank A (ma niższą efektywną stopę oprocentowania kredytów).
Zad. 9 (?)
Zad. 10
Jaka była średnia stopa procentowa w ciągu ostatnich 10 lat, jeżeli bank zmieniał sposoby naliczania odsetek w następujący sposób:
w ciągu trzech pierwszych lat stosował stopę dyskontową d=0,2
w ciągu trzech kolejnych lat intensywność oprocentowania wynosiła δ=0,18
przez 4 ostatnie lata obowiązywała stopa procentowa i=0,16
![]()
stopa procentowa równoważna stopie dyskontowej 0,2:
![]()
stopa procentowa równoważna efektywności oprocentowania 0,18 (kapitalizacja ciągła):
![]()
Średnia stopa procentowa:
Odp.: Średnia stopa procentowa w ciągu ostatnich 10 lat wyniosła 19,48%.
Zad. 11
Ile wynosi rata kredytu hipotecznego zaciągniętego na 10 lat na sumę 200 mln zł, jeżeli stopa dyskontowa wynosi 0,2?
![]()
Odp.: Wysokość raty równa jest 44,812 mln zł.
Zad. 12 (?)
Zad. 13
Ile wynosi rzeczywista stopa procentowa, jeżeli stopa inflacji wynosi 11%, roczna stopa procentowa wynosi 16%, a kapitalizacja jest kwartalna?
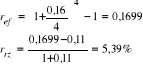
Odp.: Rzeczywista stopa procentowa wyniosła 5,39%.
Zad. 14
Jaka jest cena bieżąca obligacji 10-letniej o nominalnej cenie 5000 zł oprocentowanej 18% rocznie (odsetki płatne co roku z dołu), jeżeli do terminu wykupu pozostało 5 lat, a rynkowa stopa procentowa wynosi 16%?
![]()
Odp.: Wartość bieżąca obligacji wynosi 5327,43 zł.
Zad. 15
Dane są dwa kapitały: jeden wynosi 200 zł w dniu 01.01.1999r., a drugi 297,68 zł w dniu 01.01.2001r. Czy oba te kapitały są równoważne na dzień 01.01.2000r.? Oprocentowanie złożone, stopa procentowa 22%, kapitalizacja roczna.
Z twierdzenia dotyczącego oprocentowania złożonego wynika, że jeśli dwa kapitały są równoważne na jakiś moment w czasie, to są one również równoważne na każdy inny moment. Zatem wystarczy dowieść, że są one równoważne np. na dzień 01.01.2001r.
![]()
Kapitał o wartości 200 zł oprocentowujemy na dwa lata:
Jest on zatem równoważny kapitałowi drugiemu na dzień 01.01.2001r., a więc także na każdy inny dzień (w tym na 01.01.2000r.)
Zad. 16
Klient kupił 28-dniowy bon skarbowy opiewający na 1000 zł po cenie nominalnej 992 zł. Po 18 dniach sprzedał go na rynku wtórnym przy stopie dyskontowej 24%. Jaki był roczny realny zysk klienta?
![]()
![]()
Obliczam dyskonto emitenta bonu:
Obliczam dyskonto rynkowe 28-dniowe (tzn. wyrażone w tym samym okresie co dyskonto emitenta):
Miesięczny (28-dniowy) zysk realny klienta wynosi: 0,8% - 1,87% = -1,07% (strata)
Zatem roczny zysk realny klienta wynosi ok.: 12 x (-1,07%) = -12,84% = -0,1284 (strata)
Zad. 17
Jaka jest wartość bieżąca rent wypłacanych kwartalnie z góry przez 10 lat w wysokości 5000 zł, jeżeli roczna stopa procentowa wynosi 20%, a kapitalizacja jest kwartalna?
![]()
Zad. 18 (?)
Zad. 19
Po ilu kwartałach kapitał potroi swą wartość, jeżeli zakładamy oprocentowanie złożone, kapitalizację kwartalną z góry oraz roczną stopę dyskontową d=0,16?
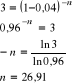
Odp.: Po 27 kwartałach (dokładnie po 26,91 kwartałach).
Zad. 20
Jaka jest wartość bieżąca (t=0 początek roku) ciągu dwóch płatności - jednej w wysokości 300 zł na koniec marca oraz drugiej w wysokości 500 zł na koniec września? Oprocentowanie proste z roczną stopą dyskontową 0,2.
![]()
Dyskontujemy obie wartości na dzień t=0, czyli 01.01.:
Odp.: Wartość bieżąca tego ciągu płatności wynosi 710 zł.
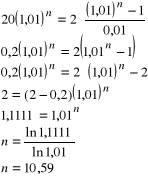
![]()
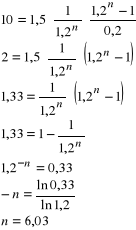
![]()
![]()
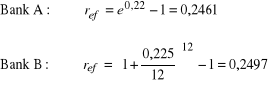
![]()
![]()
![]()
![]()
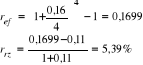
![]()
![]()
![]()
![]()
![]()
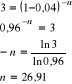
![]()
Wyszukiwarka
Podobne podstrony:
Matematyka finansowa zadania z rozwiązaniami 2
Matematyka finansowa zadania z rozwiązaniami
Zadania z rozwiązaniem - matematyka finansowa, Zadania
matematyka finansowa zadania z wykladu
Matematyka finansowa - zadania 2
Matematyka finansowa - zadania, Zadanie 13
Matematyka finansowa zadania
Matematyka finansowa - zadania 2, INNE KIERUNKI, matematyka
Matematyka finansowa zadania 2
Matematyka finansowa - zadania, INNE KIERUNKI, matematyka
MATEMATYKA FINANSOWA-ZADANIA 2
matematyka finansowa zadania z wykladu
więcej podobnych podstron