ZADANIE 1
Czas zdatności obiektu może być opisany rozkładem wykładniczym. Jakie jest prawdopodobieństwo tego, że po upływie czasu równego oczekiwanemu czasowi zdatności tego obiektu, obiekt ten będzie jeszcze zdatny?
![]()
![]()
Odp.: 0,36.
ZADANIE 2
Czas zdatności urządzenia opisany jest rozkładem wykładniczym. Jaki co najmniej musi być oczekiwany czas zdatności tego urządzenia, aby przed upływem 100 godzin jego pracy funkcja niezawodności nie przyjęła wartości mniejszych od 0,99.
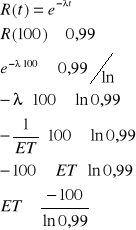
Jak się dzieli obie strony przez liczbę mniejszą od 0, to zmieniamy znak.
Odp.: ![]()
ZADANIE 3
Stwierdzono, że intensywność uszkodzeń pewnego urządzenia jest wprost proporcjonalna do czasu jego pracy. Oblicz funkcję niezawodności tego urządzenia.
![]()
; a - proporcjonalność
Wzór WIENERA ![]()
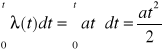
![]()
ZADANIE 4
Stwierdzono, że gęstość prawdopodobieństwa uszkodzeń można przedstawić w postaci zależności:
![]()
. Oblicz funkcję niezawodności, intensywności uszkodzeń i oczekiwany czas zdatności tych urządzeń.
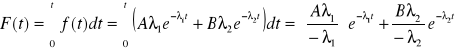
![]()
![]()
Funkcja niezawodności
![]()
Intensywność uszkodzeń
![]()
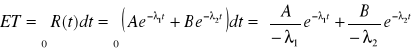
![]()
![]()
Ten sam wyrób produkują dwa zakłady: zakład A, produkujący x % oraz zakład B produkujący y %.
x + y = 100%.
Jeden produkuje trochę lepiej, drugi gorzej.
ZADANIE 5
Stwierdzono, że funkcja niezawodności pewnych urządzeń ma postać:
![]()
Obliczyć gęstość prawdopodobieństwa uszkodzeń tych urządzeń.
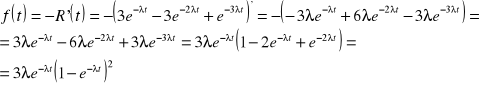
ZADANIE 6
(POTENCJALNE EGZAMINACYJNE)
Urządzenie o szeregowej strukturze niezawodnościowej składa się z II jednakowych elementów, których funkcje niezawodnościowe są znane. Obliczyć intensywność uszkodzeń urządzenia.
(tramwaj)
R1(t) R2(t)
![]()
gdzie:
λ - intensywność uszkodzeń U - urządzenia
![]()
→→→ ![]()
→→→
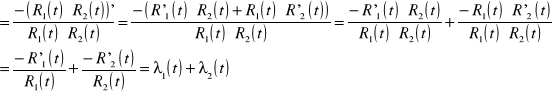
Odp.: ![]()
ZADANIE 7
Urządzenie o równoległej strukturze niezawodnościowej składa się z II jednakowych elementów, których
intensywność uszkodzeń nie zależy od czasu pracy urządzenia. Oblicz ile razy oczekiwany czas zdatności urządzenia przewyższa oczekiwany czas zdatności elementu.
λ
λ
![]()
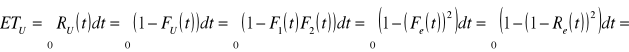
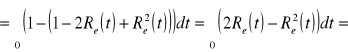
![]()
→→→ →→→
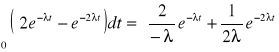
![]()
![]()
![]()
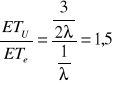
Odp.: 1,5.
ZADANIE 8
Urządzenie o równoległej strukturze niezawodnościowej składa się z III jednakowych elementów, których czasy zdatności opisane są rozkładem jednostajnym na przedziale od 0 do a. Stwierdzono, że oczekiwany czas zdatności tego urządzenia wynosi 90 jednostek czasu. Oblicz gęstość prawdopodobieństwa uszkodzeń elementów.
![]()
![]()
![]()
- kres górny czasu zdatności elementu
fe(t)
1/a
α t
![]()
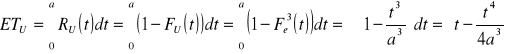
![]()
![]()
![]()
Odp.: ![]()
ZADANIE 9
Urządzenie o równoległej strukturze niezawodnościowej składa się z n jednakowych elementów, których czasy zdatności opisane są rozkładem jednostajnym na przedziale od 0 do k. ![]()
Stwierdzono, że oczekiwany czas zdatności tego urządzenia jest 1,8 raza większy od oczekiwanego czasu zdatności elementu. Z ilu elementów składa się to urządzenie?
![]()
![]()
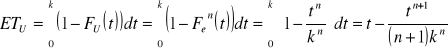
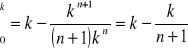
![]()
![]()
![]()
Odp.: n = 9
ZADANIE 10
Urządzenie o strukturze mieszanej przedstawionej na rysunku składa się z 4 jednakowych elementów, których czasy zdatności opisane są rozkładem wykładniczym o parametrze λ. Oblicz oczekiwany czas zdatności tego urządzenia.
A B
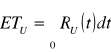
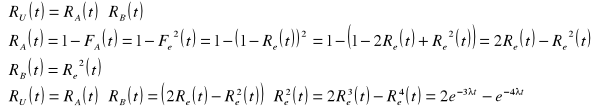
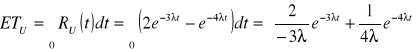
![]()
![]()
Odp.: ![]()
.
ZADANIE 11
Urządzenie o strukturze niezawodnościowej przedstawionej na rysunku, składa się z 6 jednakowych elementów, których intensywność uszkodzeń nie zależy od czasu ich pracy. Obliczyć do jakiej wartości dąży intensywność uszkodzeń urządzenia, gdy czas jego pracy dąży do +∞.
B
C
A
C
Funkcja niezawodności elementu opisana jest funkcją wykładniczą.
![]()
![]()
intensywność uszkodzeń: ![]()
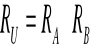
![]()
to jest zawodność elementu
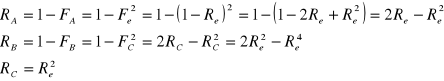
![]()
![]()
![]()
![]()
![]()
(skracamy przez ![]()
) = ![]()
![]()
ZADANIE 12
Urządzenie składa się z elementu podstawowego i jednego elementu rezerwowego będącego rezerwą nieobciążoną. Czasy zdatności elementów opisane są rozkładami wykładniczymi o jednakowych parametrach = λ. Obliczyć funkcję niezawodności, gęstość prawdopodobieństwa uszkodzeń i oczekiwany czas zdatności tego urządzenia.
1
2
Czas zdatności ![]()
Dystrybuantą sumy zmiennych losowych niezależnych
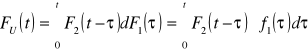
t
f1(τ)dτ - prawdopodobieństwo tego, że element 1 uszkodził się w „chwili” δ (w bardzo małym przedziale czasu, którego środkiem jest δ); F2(t - τ) prawdopodobieństwo tego, że element drugi przepracował mniej niż (t - δ) jednostek czasu.
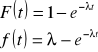
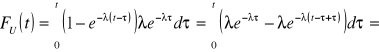
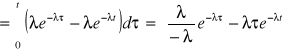
![]()
![]()
Funkcja niezawodności
![]()
![]()
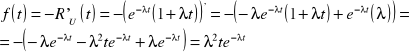
![]()
Wartość oczekiwana sumy niezależnych zmiennych losowych = sumie wartości oczekiwanych tych zmiennych losowych.
![]()
![]()
ZADANIE 13
Urządzenie z rezerwą nieobciążoną. Intensywność uszkodzeń nie zależy od czasu pracy. Obliczyć funkcję niezawodności urządzenia.
![]()
![]()
- gdyż elementy te „są połączone” szeregowo
![]()
ZADANIE 14
Urządzenie o strukturze niezawodnościowej, przedstawionej na rysunku składa się z III jednakowych elementów, których intensywności uszkodzeń nie zależą od czasu ich pracy. Obliczyć intensywność uszkodzeń urządzenia.
![]()
![]()
![]()
![]()
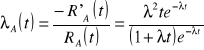
![]()
ZADANIE 15
Urządzenie o szeregowej strukturze niezawodnościowej, składa się z 20 elementów. W rozpatrywanej chwili czasu wartość funkcji niezawodności każdego z tych elementów jest równa ![]()
. Dysponujemy 40-stoma elementami rezerwowymi, które mogą być wykorzystane do rezerwowania ogólnego lub indywidualnego tego urządzenia.
0,9 - niezawodność
Obliczyć wartość funkcji niezawodności urządzenia w rozpatrywanej chwili bez rezerwowania oraz w przypadku rezerwowania ogólnego i indywidualnego (rezerwa obciążona)
Bez rezerwowania
![]()
Rezerwowanie ogólne
![]()
Rezerwowanie indywidualne
![]()
Wnioski!!!
Urządzenie o niezawodności haniebnej!!! Ru = 0,12.
Niezawodność 3x podnosimy przy rezerwowaniu ogólnym - niezawodność nadal podła Ruo = 0,32.
Przy rezerwowaniu indywidualnym podnosimy 8x → jest O.K.
ZADANIE 16
Urządzenie o równoległej strukturze niezawodnościowej, składa się z II jednakowych elementów. Intensywność uszkodzeń elementu = λ, a intensywność jego odnowy wynosi μ. Obliczyć stacjonarny współczynnik gotowości tego urządzenia, zakładając, że nie występują żadne ograniczenia co do liczby elementów, które mogą być jednocześnie odnawiane i nie występują tzw. uszkodzenia o wspólnej przyczynie. EGZAMIN!!!
Stany:
0 - wszystkie elementy zdatne,
1 - jeden element niezdatny,
2 - dwa elementy niezdatne
Ponieważ nie uwzględniamy uszkodzeń o wspólnej przyczynie, tego przejścia nie nanosimy na grafie
Układ równań (układ równań tożsamościowych czyli trzecie wynika z dwóch wcześniejszych):
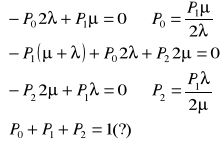
Ostatnie równanie tworzymy korzystając z warunku normującego (konieczne jest wprowadzenie warunku normującego)
Mamy teraz IV równania i trzy niewiadome... Co robimy? !!! Pozbywamy się najdłuższego (tj. 2)
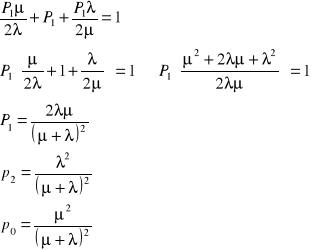
Stacjonarny współczynnik gotowości urządzenia kg.
Urządzenie ma strukturę równoległą - gdy co najmniej jeden element jest zdatny to urządzenie jest zdatne co można zapisać jak niżej:
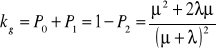
ZADANIE 17
Urządzenie o równoległej strukturze niezawodnościowej, składa się z II jednakowych elementów, których intensywność uszkodzeń i odnowy wynoszą odpowiednio λ i μ. Obliczyć stacjonarne prawdopodobieństwo tego, że w urządzeniu nie ma elementów uszkodzonych, przy założeniu, że uszkodzone elementy są odnawiane kolejno.
2λ λ
0 1 2
μ μ
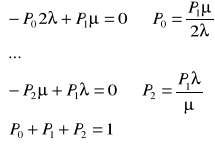
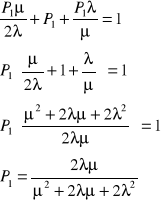
![]()
ZADANIE 19
Urządzenie składa się z elementu podstawowego i jednego elementu rezerwowego. Intensywność uszkodzeń elementu jest równa λ1 w okresie pracy i λ2 w okresie rezerwowania. Uszkodzone elementy są odnawiane kolejno, a intensywność odnowy jest równa μ. Obliczyć stacjonarny współczynnik gotowości tego urządzenia, gdy element rezerwowy będzie rezerwą:
obciążoną
nieobciążoną
częściowo obciążoną
Wypisujemy stany:
0 - wszystkie elementy zdatne
1 - jeden element niezdatny
2 - dwa elementy niezdatne
Ad. c
λ1 + λ2 λ1
2
1
0
μ
μ
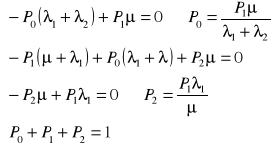
usuwamy największe
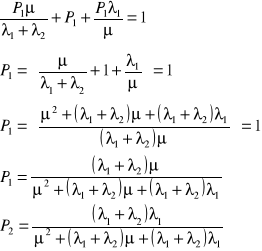
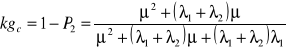
Ad. a
λ1 + λ1 1 λ1
0
0 2
μ μ
μ
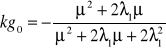
Ad. b
λ1 λ1
0 1 2
μ
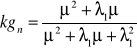
Nie ma sensu liczyć gdy można wykorzystać fakt, że dla przypadku a) λ2 = λ1, a w przypadku b) λ2 = 0.
ZADANIE 20
Czas zdatności urządzenia między kolejnymi uszkodzeniami opisany jest rozkładem wykładniczym. Zakładając, że czas odnowy uznajemy za pomijalnie mały, obliczyć dystrybuantę czasu pracy tego urządzenia do III uszkodzenia.
Oś czasu
T T T
0 1 2 3
Zmienna losowa ma rozkład wykładniczy.
Dystrybuanta czasu do drugiego uszkodzenia była wyprowadzona w jednym z poprzednich zadań
![]()
Korzystamy ze wzoru rekurencyjnego:
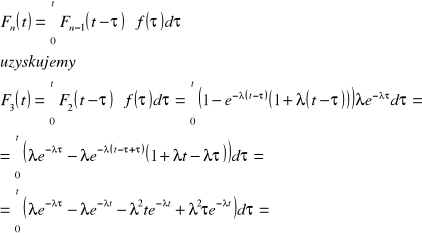
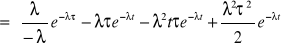
![]()
![]()
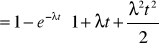
ZADANIE 21
Oczekiwany czas zdatności urządzenia jest znany i wynosi 10 lat. Urządzenie to do chwili obecnej bezawaryjnie przepracowało 4 lata. Ile wynosi oczekiwany pozostały czas zdatności tego urządzenia, jeżeli czas jego zdatności jest zmienną losową o rozkładzie wykładniczym, a ile jeśli zmienną losową o rozkładzie jednostajnym z kresem dolnym = 0.
W przypadku rozkładu wykładniczego, pozostały czas zdatności urządzenia równa się oczekiwanemu czasowi zdatności urządzenia = 10 lat.
Przy rozkładzie jednostajnym:
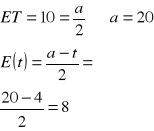
ZADANIE 22
Urządzenie o strukturze niezawodnościowej przedstawionej na schemacie składa się z III jednakowych elementów. Czas zdatności elementu opisany jest rozkładem jednostajnym o kresie dolnym = 0. Oczekiwany czas zdatności urządzenia jest znany i równy 1000 godzin. Obliczyć:
oczekiwany czas zdatności elementu
oczekiwany czas zdatności urządzenia
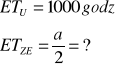
f(t)
![]()
a
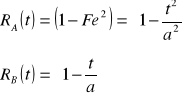
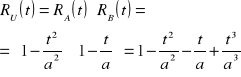
funkcja niezawodności
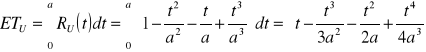
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
teoria niez, Zadania z niezawodności ok, ZADANIE 1
teoria niez, ZADANIE 1, ZADANIE 1
Algebra z geometrią teoria, przykłady, zadania
FUNKCJA KWADRATOWA teoria oraz zadania
Teoria ryzyka - zadania, STUDIA
teoria niez, Teoria niezawodności
teoria gier zadanie K6ALSIDLZEKVSGXKBVI6IMHVAVXRNTMUBWM5WOY
Gewert, Skoczylas Równania różniczkowe zwyczajne , teoria przykłady, zadania
Gewert M, Skoczylas Z Wstęp do analizy i algebry Teoria, przykłady, zadania wyd 2
cz1 teoria czwórników zadania
cz1 teoria czwórników zadania
Logistyka [ teoria], MRP zadanie1, HARMONOGRAM ZAPOTRZEBOWANIA - ZADANIE 2
raporty, teoria1, Celem zadania jest pomiar siły elektromotorycznej SEM generowanej w ogniwie organi
FUNKCJA WYKŁADNICZA – teoria oraz zadania
CIĄGI – teoria oraz zadania
Teoria maszyn zadania
DZIAŁANIA NA LOGARYTMACH teoria oraz zadania
TRYGONOMETRIA – teoria oraz zadania
więcej podobnych podstron