Ć w i c z e n i e 7

WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY

PODCZAS JEJ PRZEPŁYWU PRZEZ KAPILARĘ

7.1 Opis teoretyczny

Lepkość jest to właściwość cieczy i gazów polegająca na powstawaniu w nich naprężeń stycznych
zależnych od prędkości przesuwania się warstw cieczy.
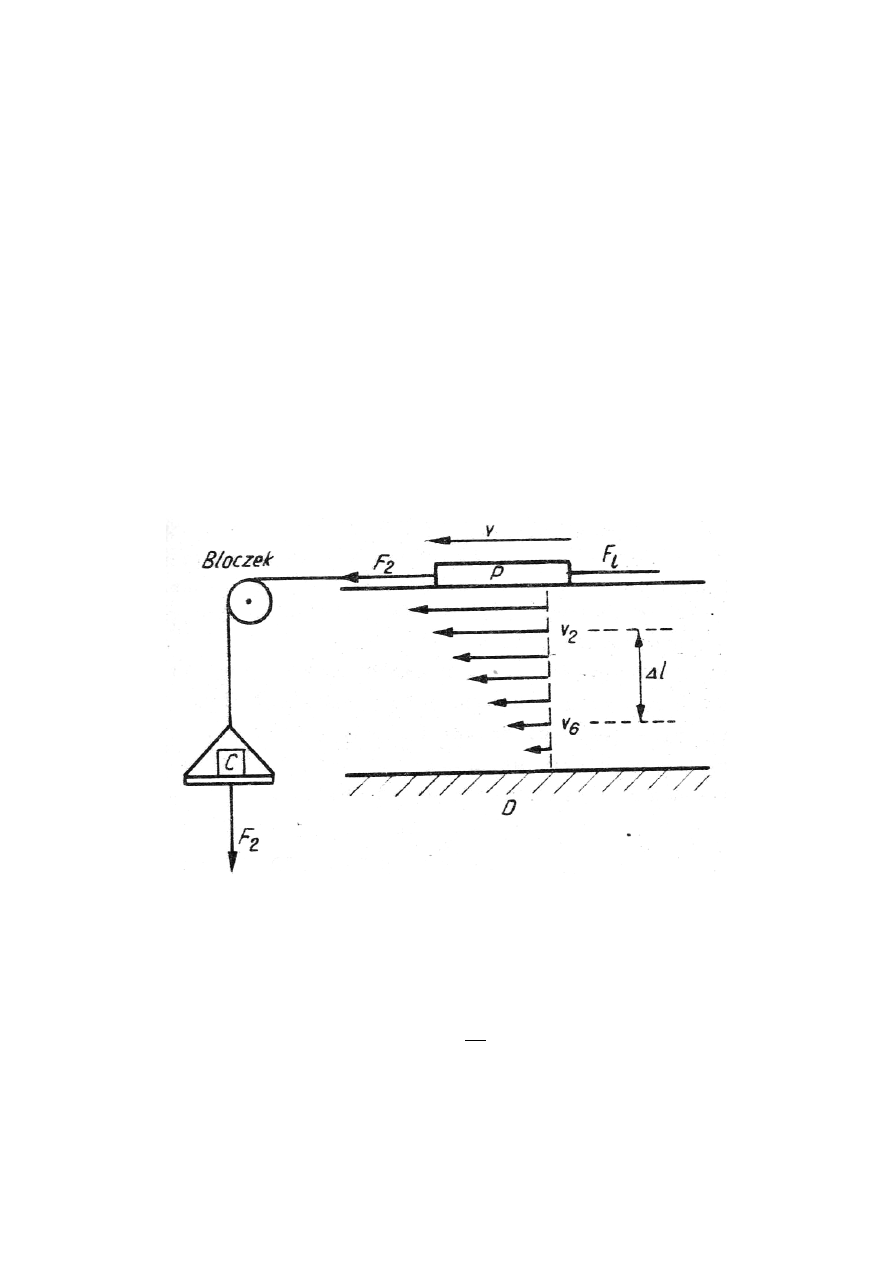
Zasadę pomiaru oporu lepkości cieczy przedstawia rys.7.1. Na płycie D została rozlana warstwa
cieczy, na której spoczywa płytka P. Szalka z ciężarkiem C wprawia płytkę w ruch (działa siła F

2

).

Sile F

2

przeciwstawia się siła tarcia wewnętrznego cieczy F

1

, gdyż płytka pociąga za sobą najbliż-

szą przylegającą warstewkę cieczy, a ta z kolei pociąga z nią sąsiadującą położoną pod nią itd.
(dzieje się tak, gdyż działają przyciągające siły cząsteczkowe między cząsteczkami cieczy jak i
między cząsteczkami cieczy i cząsteczkami płytki i podłoża).W ten sposób warstewki górne poru-
szają się szybciej niż warstewki dolne. Zjawisku towarzyszy więc określony gradient prędkości
dv/dl.

Rys.7.1. Zasada pomiaru oporu lepkości cieczy

Eksperymentalnie możemy tak dobrać ciężarek C, aby płytka P poruszała się ruchem jednostajnym
i wówczas F

2

= F

1

. W ten sam sposób można wyznaczyć wielkość siły F

1

. Na bazie takich do-

świadczeń ustalono, że siła F

1

jest proporcjonalna do powierzchni S płytki oraz gradientu prędkości

dv/dl. Wyraża to wzór

dl

dv

S

η

F

1

=

(7.1)

gdzie

η jest współczynnikiem lepkości (zwanym również lepkością dynamiczną), charakteryzują-

cym wielkość wzajemnego oddziaływania cząsteczek w danej cieczy.

Jak łatwo sprawdzić, jednostką współczynnika lepkości w układzie SI jest Ns/m

2

, czyli paskalose-

kunda. Stosuje się też zwyczajowo jednostkę zwaną puaz (skrót P) od nazwiska francuskiego bada-
cza Poiseuille'a, przy czym 1Ns/m

2

= 10 P). Lepkość dynamiczna wody w temperaturze 20

0

C jest

bardzo bliska wartości 1 centypuaza (1cP = 10

-2

P = 10

-3

Ns/m

2

) (tabl. 7). Widzimy więc, że współ-

czynnik lepkości zależy nie tylko od rodzaju cieczy, ale również od temperatury. Ze wzrostem ru-
chu termicznego cząsteczek, siły międzycząsteczkowe słabną, a więc również maleje

η. Zależność

η = f(T) jest zależnością wykładniczą , co można zapisać:

T

B

e

A

η

=

(7.2)

gdzie: A i B - stałe charakteryzujące daną ciecz, T - temperatura [K].

Siła oporu lepkości występuje w dwóch typach zjawisk:
1. Podczas ruchu cieczy względem nieruchomych ścianek naczynia - doświadczalnie realizowane

w tym ćwiczeniu.

2. Podczas ruchu ciała względem nieruchomej cieczy - wyznaczanie współczynnika lepkości me-

todą Stokesa (patrz ćwicz.8).

Rys.7.2. Rozkład prędkości laminarnego przepływu cieczy w rurce.

Rysunek 7.2. przedstawia rozkład prędkości przy laminarnym przepływie cieczy przez rurkę. W
przepływie laminarnym (czyli warstwowym) cieczy, poszczególne jej warstewki charakteryzujące
się stałymi prędkościami ruchu trą o siebie, ale nie zaburzają wzajemnie swojego ruchu. Nie ma
wymiany cząsteczek między warstwami.

Chcąc pokonać opór lepkości cieczy F

1

należy zastosować różnicę ciśnień

∆p = p

1

- p

2

między jed-

nym końcem rurki a drugim i tylko wówczas możemy obserwować wypływ cieczy z cienkiej rurki.
Objętość V cieczy wypływającej z cienkiej rurki w czasie t można znaleźć stosując zasadnicze rów-
nanie lepkości (wzór 7.1) oraz znany w tym wypadku paraboliczny rozkład prędkości ( rys.7.2).

t

d

η

8

∆p

r

π

V

4

=

( 7.3)

gdzie: d - oznacza długość rurki (kapilary).

Wzór ten wyraża prawo Poiseuille'a opisujące laminarny przepływ cieczy przez cienkie rurki. Pra-
wo to często przedstawia się w powiązaniu ze średnią prędkością wypływu cieczy z rurki.
Dla jednostkowego czasu (np. t = 1 s ) można zapisać:

v

r

π

t

V

2

=

(7.4)

gdzie:

v - jest średnią prędkością laminarnego przepływu cieczy.

Korzystając z tej zależności i ze wzoru (7.3) otrzymujemy wyrażenie na średnią prędkość przepły-
wu cieczy

d

η

8

∆p

r

v

2

=

(7.5)

Średnia prędkość przepływu cieczy przez cienką rurkę jest wprost proporcjonalna do różnicy ci-
śnień i kwadratu promienia rurki, a odwrotnie proporcjonalna do jej długości i lepkości dynamicz-
nej cieczy.
Powyższe wzory są słuszne jedynie dla przepływu laminarnego. Dlatego też ważne jest kryterium
przepływu laminarnego cieczy. Jest nim wartość liczby Reynoldsa zdefiniowanej wyrażeniem:

η

ρ

v

r

2

Re

=

(7.6)

gdzie

ρ oznacza gęstość cieczy.

Gdy wartość Re jest mniejsza od pewnej wartości krytycznej (Re<Re

kr

), to mamy do czynienia z

przepływem warstwowym, w przeciwnym razie z przepływem burzliwym. Dla przepływu cieczy
przez rurkę Re

kr

= 2300.

W ćwiczeniu przeprowadzamy pomiar współczynnika lepkości metodą względną, tzn. porównując
ciecz o nieznanym

η z cieczą wzorcową o znanym η = η

0

. W naszym przypadku cieczą wzorcową

jest woda destylowana. W tym celu wystarczy zmierzyć czas przepływu równych objętości obu
cieczy przez tę samą rurkę (kapilarę) w jednakowych warunkach. Wówczas stosując wzór Poiseuil-
le'a (7.3) otrzymujemy:

a) dla cieczy wzorcowej:

0

0

0

4

t

d

η

8

∆p

r

π

V

=

(7.7)

b) dla cieczy badanej:

t

d

η

8

∆p

r

π

V

4

=

(7.8)

Porównując równania (7.7) i (7.8) otrzymujemy:

0

0

0

t

∆p

t

∆p

η

η

=

(7.9)

Jeżeli przepływ cieczy w rurce zachodzi pod wpływem własnego ciężaru (jak w wiskozymetrze
Ostwalda), to różnice ciśnień wynoszą odpowiednio:

śr

0

0

h

g

ρ

∆p

=

śr

h

g

ρ

∆p

=

gdzie:

ρ, ρ

0

- gęstość cieczy, h

śr

- średnia wysokość słupa cieczy podczas przeprowadzania pomia-

ru.

Stąd

0

0

0

t

t

η

η

ρ

ρ

=

(7.10)

7.2 Opis układu pomiarowego

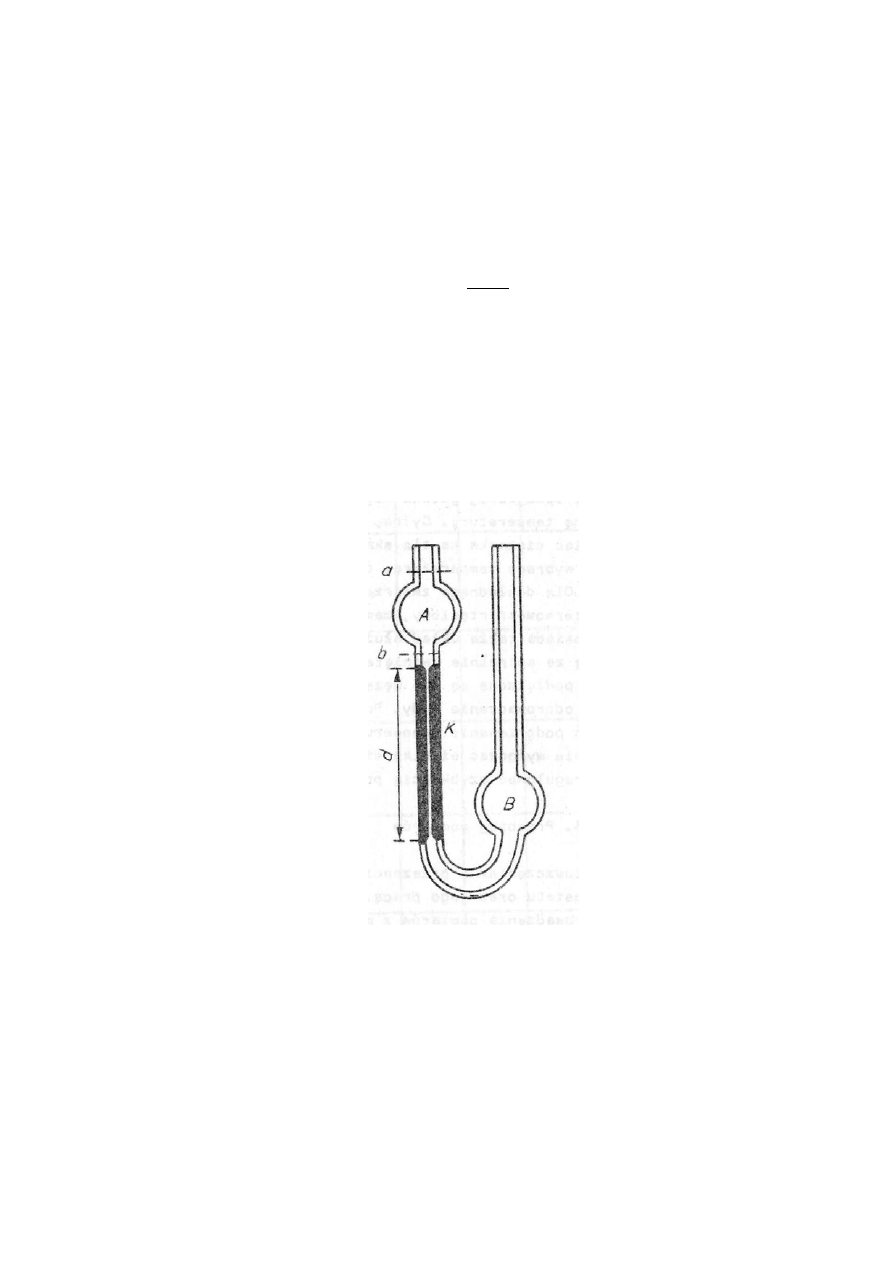
W ćwiczeniu do pomiaru lepkości cieczy zastosowano wiskozymetr Ostwalda (rys.7.3) przeznaczo-
ny do szybkich pomiarów względnych. Jest on zbudowany z dwóch zbiorniczków A i B umiesz-
czonych na różnych poziomach i połączonych ze sobą U - rurką. Na jej kilkucentymetrowym od-
cinku znajduje się przewężenie kapilarne K. Górny zbiorniczek (A) służy za miarę objętości prze-
pływającej cieczy i dlatego jego górny oraz dolny poziom jest zaznaczony kreskami a i b.

Rys.7.3. Wiskozymetr Ostwalda

Chcąc zmierzyć względny współczynnik lepkości badanej cieczy wlewamy ją do wiskozymetru
przez szersze ramię, aż do wypełnienia dolnego rozszerzenia rurki. Napełniając następnie przez
wessanie górną bańkę, mierzymy czas jej opadania między zaznaczonymi na szkle kreskami. Tak
samo mierzymy czas przepływu cieczy wzorcowej. Ponieważ współczynnik lepkości zależy od
temperatury, wiskozymetr umieszcza się w termostacie, którego temperaturę można regulować.
Urządzenia termostatu używanego w ćwiczeniu są doskonale widoczne, ponieważ jego obudowę
stanowi szklane akwarium. Aby je uruchomić, należy włączyć silnik poruszający mieszadełko słu-
żące do wyrównania temperatury kąpieli oraz włączyć układ podgrzewający kąpiel termostatu.
Włączenie i wyłączenie podgrzewania odbywa się automatycznie za pomocą termoregulatora (tzw.
termometr stykowy). Sygnałem włączenia grzałki jest zapalenie się neonowej lampki. Nastawienie

termoregulatora na żądaną temperaturę odbywa się za pomocą specjalnej główki magnetycznej.
Kręcąc nią można ustalić żądaną temperaturę. Cyfra, naprzeciw której zatrzyma się górny koniec
ciężarka na tle skali termometrycznej, oznacza w przybliżeniu wybraną temperaturę, do której na-
grzeje się kąpiel termometru. Dla dokładnego zmierzenia temperatury kąpieli służy oddzielny ter-
mometr rtęciowy, zamocowany w pokrywie termostatu. Termostat posiada także układ służący do
chłodzenia kąpieli, składający się ze spiralnie zwiniętej metalowej rurki (chłodnicy), do której pod-
łączone są dwa węże - jeden do sieci wodociągowej, drugi do odprowadzania wody. Przy chłodze-
niu termostatu należy wyłączyć podgrzewanie (manewrując odpowiednio główką magnetyczną) i
nie wyłączać silnika mieszadełka. Szybkość chłodzenia można regulować szybkością przepływu
wody.

7.3. Przebieg pomiarów

1. Zapoznać się z rozmieszczeniem i przeznaczeniem poszczególnych elementów termostatu oraz

jego pracą.

2. Wiskozymetr wyjąć z termostatu i dokładnie przepłukać wodą destylowaną.
3. Napełnić za pomocą pipety zbiornik B wiskozymetru wodą destylowaną do 3/4 jego objętości,

zanotować objętość zużytej wody ( pipeta posiada podziałkę w cm

3

). Wiskozymetr ustawić na

jego stałe miejsce do wnętrza termostatu i zamocować go za pomocą przeznaczonej do tego
śruby.

4. Sprawdzić za pomocą termometru, czy temperatura kąpieli jest równa lub niższa od temperatury

otoczenia. Jeżeli jest wyższa, obniżyć ją przez włączenie silnika mieszadełka i chłodzenia, pa-
miętając o ustawieniu termoregulatora na temperaturę niższą od temperatury otoczenia.

5. Ustawić termoregulator na temperaturę 20

0

C, odczekać aż lampka neonowa zgaśnie, po czym

wciągnąć za pomocą gruszki gumowej wodę ze zbiornika B do zbiornika A tak, aby górny po-
ziom wody znalazł się powyżej kreski a.

6. Odłączyć gruszkę i zmierzyć czas wypływu wody z objętości zawartej pomiędzy kreskami a i b.
7. Czynności z punktów 5 i 6 powtórzyć pięciokrotnie.
8. Zmierzyć czas przepływu wody jeszcze przy temperaturze 25, 30, 35 i 40

0

C (ważne jest, aby

różnica pomiędzy kolejnymi pomiarami wynosiła około 5

0

C), postępując tak jak w punktach 5 i

6.

9. Czynności według punktów 5-8 wykonać dla alkoholu etylowego (dokładnie w taki sam sposób

i dla takich samych temperatur jak w przypadku wody). Przy zmianie wody na alkohol, należy
wiskozymetr przemyć dwukrotnie alkoholem. Przy pomiarach objętości alkoholu powinna być
taka sama objętość wody. Po zakończeniu pomiarów alkohol z wiskozymetru wlać do przygo-
towanej butelki.

10. Obliczyć średnie czasy przepływu cieczy t

0

śr

i t

śr

oraz

oszacować błędy ich wyznaczania

s

t

0

śr

i

s

t

śr

.

Wpisać je do tabeli 7.1.

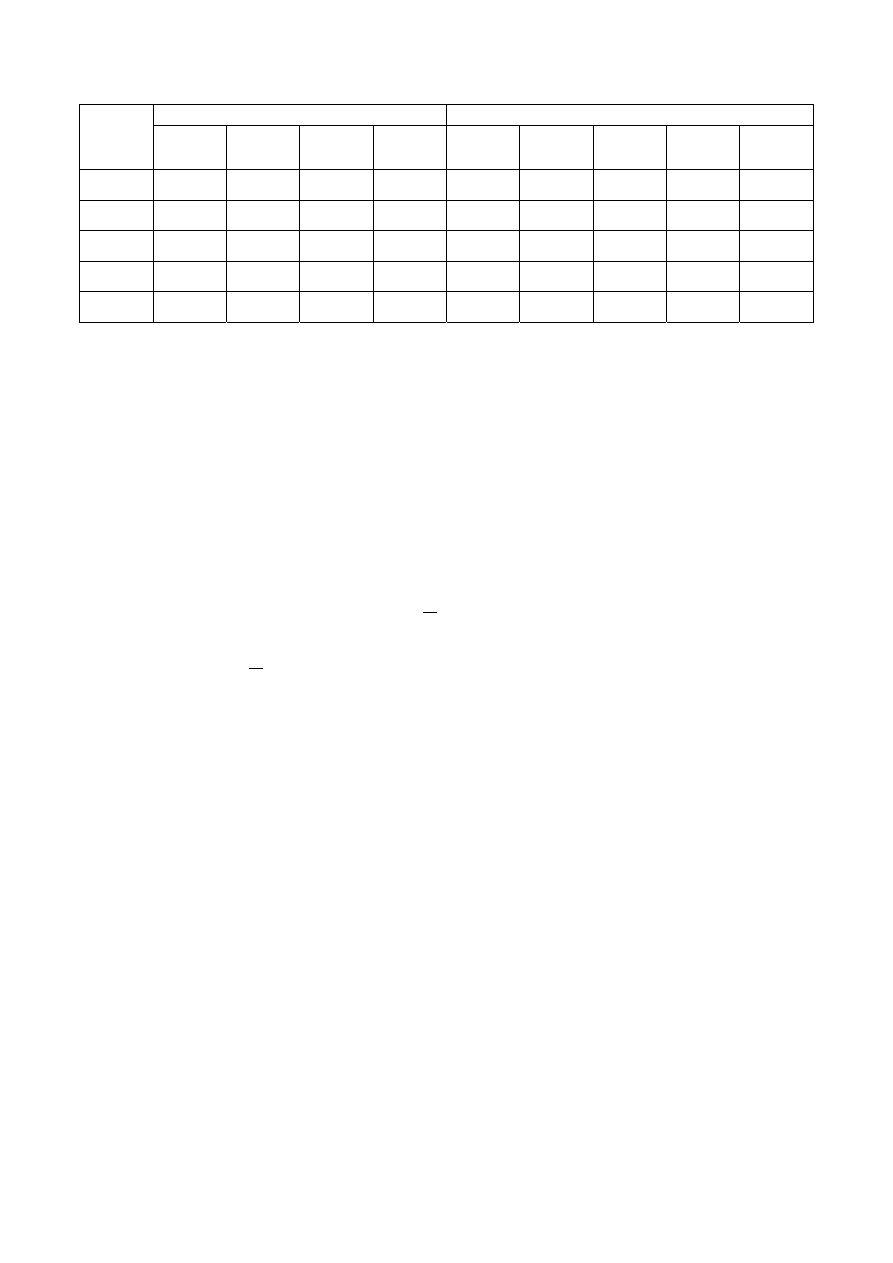
Tabela 7.1

Woda Alkohol

T

[

°C]

t

0

śr

[s]

St

0

śr

[s]

ρ

0

[g/cm

3

]

η

0

[Ns/m

2

]

t

śr

[s]

St

śr

[s]

ρ

[g/cm

3

]

η

[Ns/m

2

]

S

η

[Ns/m

2

]

T

1

T

2

T

3

T

4

T

5

7.4. Opracowanie wyników pomiarów.

1. Uzupełnić tabelę 7.1 o dane tablicowe dla wartości

η

0

,

ρ

0

,

ρ .

2. Korzystając ze wzoru (7.10) obliczyć współczynniki lepkości alkoholu dla wszystkich mierzo-

nych temperatur.

3. Zakładając, że stałe tablicowe

η

0 ,

ρ

0

,

ρ nie są obarczone błędami, obliczyć metodą różniczki

zupełnej (patrz wzór (W.2.12) we wstępie) bezwzględne odchylenie średnie

s

η

dla wszystkich

temperatur.

4. Logarytmując naturalnie zależność ( 7.2) otrzymujemy:

T

1

B

η

+

lnA

ln

=

Funkcja

]

T

1

[

F

lnη

=

jest więc linią prostą. Na podstawie danych doświadczalnych sporządzić

wykres tej funkcji. Z nachylenia prostej wyznaczyć współczynnik B, a z jej przecięcia z osią
rzędnych wielkości ln A oraz A.

5. Ocenić stopień laminarności strumienia cieczy w rurce kapilarnej, obliczając liczby Reynoldsa

według wzorów (7.6) i (7.4). Obliczenia przeprowadzić dla najwyższej temperatury, jaką miały
ciecze w warunkach naszego ćwiczenia. Średnica kapilary i objętość bańki potrzebne do obli-
czenia Re podane są przy zestawie pomiarowym.

7.5. Pytania kontrolne

1. Co nazywamy lepkością cieczy?
2. Sformułować i wyrazić wzorem prawo Poiseuille'a.
3. Sformułować kryterium laminarności przepływu cieczy.
4. Jakie warunki należy spełnić, aby wzór Poiseuille'a był słuszny?

L i t e r a t u r a

[1] Dryński T.: Ćwiczenia laboratoryjne z fizyki, PWN, Warszawa 1976.
[2] Feynman R. P., Leighton R.B., Sanos M.: Feynmana wykłady z fizyki, t.2, cz.2. PWN, W
wa 1974.

arsza-