Politechnika Rzeszowska
Wydział Budownictwa
i Inżynierii Środowiska
Katedra Konstrukcji Budowlanych

Rok akademicki 2009/2010

KONSTRUKCJE BETONOWE

PROJEKT STROPU PŁYTOWO- ŻEBROWEGO

W POMIESZCZENIU PARTERU BUDYNKU

WIELOKONDYGNACYJNEGO

temat nr

Konsultacja:

Wykonał:

PŁYTA

Zestawienie obciążeń ( obciążenia stałe)

Obciążenia zmienne

P

k

=

6

kN

m

2

γ

f

=

1,5

P

o

=

9

kN

m

2

Obciążenia całkowite:

q

k

=

g

k



P

k

=

9,385

kN

m

2

q

0

=

g

0



P

0

=

13,57

kN

m

2

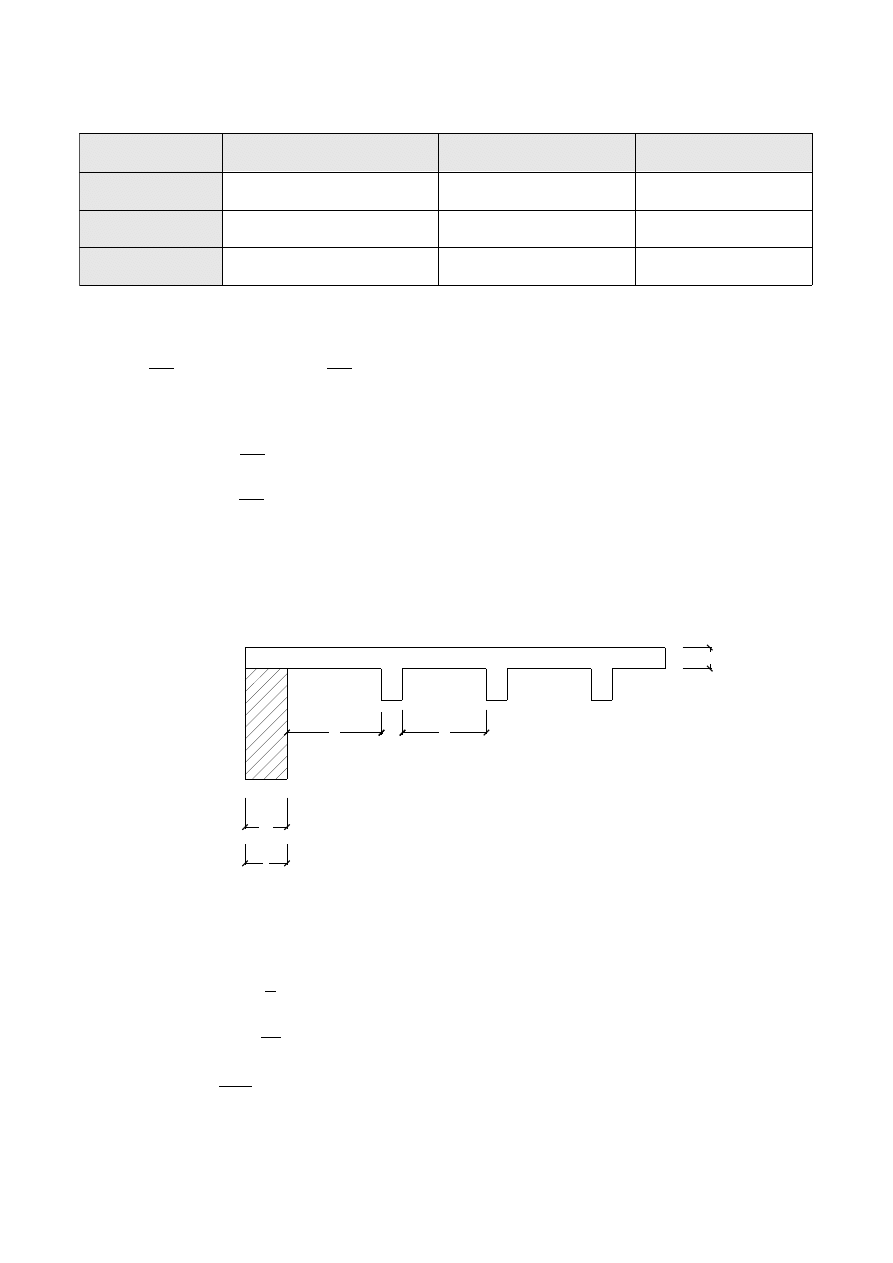
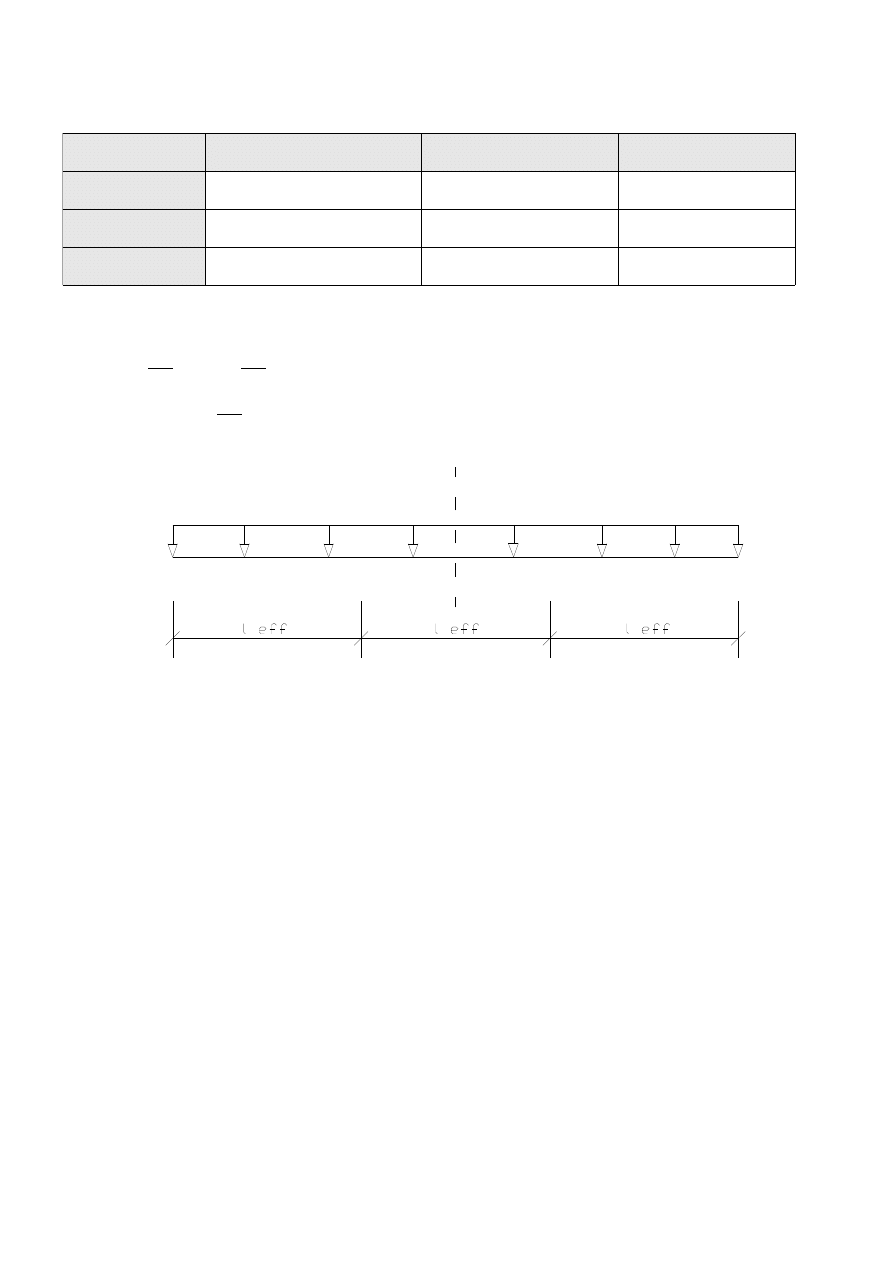
Rozpiętość przęseł

1. Przęsło skrajne

l=2 m⇒ l

n

=

2−0,25−0,1=1,65 m

l

eff

=

l

n



a

n1



1

n2

a

n1

, a

n2

=

min

{

t

2

h

f

2

}

a

n1

=

a

n2

=

0,08

2

=

0,04

l

eff 1

=

1,650,040,04=1,73 m

A

B

C

D

51

ln

ln

t

hf

20

rodzaj warstwy

obciążenie charakterystyczne

współczynnik obliczeniowy

obciążenie obliczeniowe

g( kN/ m^2)

go (kN/m^2)

Posadzka 5 cm

1,1

1,35

1,485

0,05 *22
ciężar własny płyty

2

1,35

2,700

0,08*25
ciężar tynku

0,29

1,35

0,385

0,015*19
suma

gk=3,385 kN/m^2

go=4,57 kN/m^2

2. Przęsło środkowe

l=2 m⇒ l

n

=

2−0,1−0,1=1,8 m

l

eff

=

l

n



a

n1



1

n2

a

n1

, a

n2

=

{

t

2

h

f

2

}

a

n1

=

a

n2

=

0,08

2

=

0,04

l

eff 2

=

1,80,040,04=1,88 m

Momenty przęsłowe i podporowe, siły poprzeczne

a) przęsłowe

M

1

=

a⋅g

o

⋅

l

eff1

2



b⋅P

o

⋅

l

eff1

2

=

0,0781⋅4,57⋅1,73

2



0,1⋅9⋅1,73

2

=

3,76 kNm

M

2

=

a⋅g

o

⋅

l

eff2

2



b⋅P

o

⋅

l

eff2

2

=

0,0331⋅4,57⋅1,88

2



0,0787⋅9⋅1,88

2

=

3,65 kNm

M

3

=

a⋅g

o

⋅

l

eff3

2



b⋅P

o

⋅

l

eff3

2

=

0,0462⋅4,57⋅1,88

2



0,111⋅9⋅1,88

2

=

3,47 kNm

b) podporowe

M

B

=

a⋅g

o

⋅

l

eff3

2



b⋅P

o

⋅

l

eff3

2

=−

0,105⋅4,57⋅

1,731,88

2



2

−

0,119⋅9⋅

1,731,88

2



2

=−

5,05 kNm

M

C

=

a⋅g

o

⋅

l

eff3

2



b⋅P

o

⋅

l

eff3

2

=−

0,079⋅4,57⋅1,88

2

−

0,111⋅9⋅1,88

2

=−

4,81 kNm

c) siły poprzeczne

Q

AP

=⋅

g

o

⋅

l

eff

⋅

P

o

⋅

l

eff

=

0,395⋅4,57⋅1,730,447⋅9⋅1,73=10,55 kN

Q

BL

=⋅

g

o

⋅

l

eff

⋅

P

o

⋅

l

eff

=−

0,606⋅4,57⋅1,73−0,620⋅9⋅1,73=−14,44 kN

Q

BP

=⋅

g

o

⋅

l

eff

⋅

P

o

⋅

l

eff

=

0,526⋅4,57⋅1,880,598⋅9⋅1,88=14,64 kN

Q

CL

=⋅

g

o

⋅

l

eff

⋅

P

o

⋅

l

eff

=−

0,474⋅4,57⋅1,88−0,576⋅9⋅1,88=−13,87 kN

Q

CP

=⋅

g

o

⋅

l

eff

⋅

P

o

⋅

l

eff

=

0,500⋅4,57⋅1,880,597⋅9⋅1,88=14,40 kN

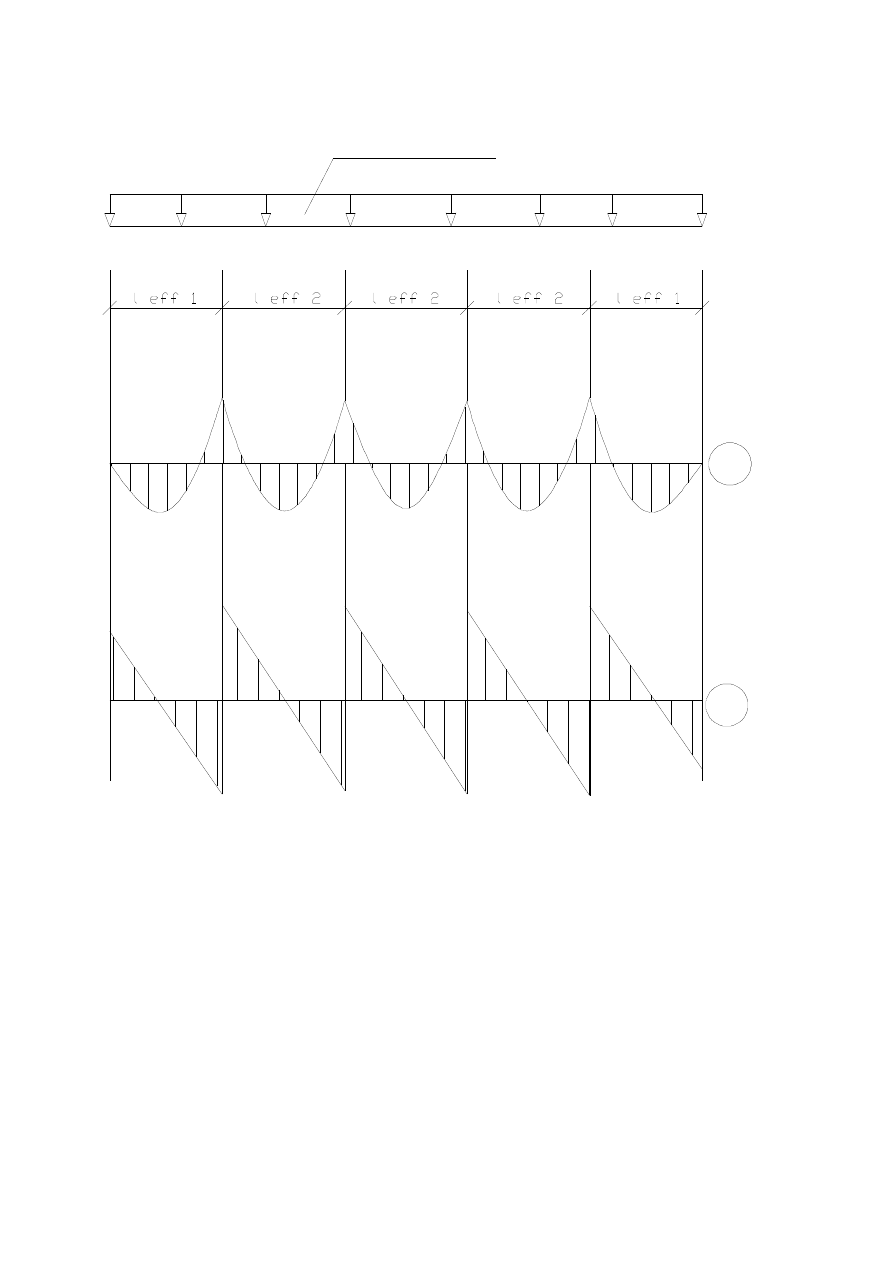
13,57 kN/m

A

B

C

D

E

F

10,55

10,55

14,44

14,64

14,40

13,87

14,44

13,87

14,40

14,64

3,73

5,05

3,65

4,81

3,47

3,65

3,73

5,05

4,81

M

Q

WYMAIROWANIE NA ZGINANIE

a

1

= 2 cm

Dobór materiałów:

•

beton C20/25,

f

ck

=

20 MPa

f

cd

=

13,3 MPa

f

ctm

=

2,2 MPa

E

cm

=

30 GPa

f

ctk

=

1,5 MPa

•

•

stal SPB B500

f

yd

=

420 MPa

f

yk

=

500 MPa

E

s

=

200 GPa

•



efflim

=

0,5

c

strzem

=

20 mm

c

zbroj.gł

=

30 mm

Przęsło skrajne:

M

Ed

=

3,76 kNm=376 kNcm

d =h−a

1

⇒

d =8−2=6cm



M

AS1

=

0 ⇒ x

eff

⋅

b⋅f

cd

⋅

b−

x

eff

2

−

M

Ed

=

0

x

eff

⋅

100⋅1,33⋅6−

x

eff

2

−

376=0

−

66,5 x

eff

2



798 x

eff

−

376=0

=

798

2

−

4⋅−66,5⋅−376=536788



=

732,7

x

eff1

=

−

798−732,7

−

2⋅66,5

=

11,518 cm x

eff2

=

−

798732,7

−

2⋅66,5

=

0,49 cm

0,49

6

=

0,0820,5 ⇒ zbrojenie pojedyncze

d

8

b=100

a1

x

eff

*b*f

cd

A

s1

*f

yd

A

s1

M

Ed

h



M A

CC

=

0

A

S1

=

M

Ed

f

cd

⋅

d −

0,51
2



=

376

42⋅6−

0,49
2



=

1,56 cm

2

Przyjęto 6 6 co 16 cm o A

S1

=

1,70 cm

2

Przęsło przyskrajne tak samo jak skrajne.

Nad podporą:

M

C

=−

5,05 kNm=−505 kNcm

d =h−a

1

⇒

d =8−2=6cm



M

AS1

=

0⇒ x

eff

⋅

b⋅f

cd

⋅

b−

x

eff

2

−

M

Ed

=

0

x

eff

⋅

100⋅1,33⋅6−

x

eff

2

−

540=0

−

66,5 x

eff

2



798 x

eff

−

505=0

=

798

2

−

4⋅−66,5⋅−505=502474



=

708,9

x

eff1

=

−

798−708,9

−

2⋅66,5

=

11,338 cm

x

eff2

=

−

798708,9

−

2⋅66,5

=

0,67 cm

0,67

6

=

0,110,5⇒ zbrojenie pojedyncze



M A

CC

=

0

A

S1

=

M

C

f

cd

⋅

d −

0,51

2



=

505

42⋅6−

0,67

2



=

2,12 cm

2

Przyjęto 8 6 co 12 cm o A

S1

=

2,26 cm

2

WYMIAROWANIE NA ŚCINANIE

V

Rd , c

=

[

C

Rd ,c

⋅

k⋅100⋅

1

⋅

f

ck



1
3



k

1

⋅

cp

]

⋅

b

w

⋅

d

C

Rd , c

=

0,18

1,5

=

0,12

k =1



200

d

=

1



200

60

=

2,832⇒ przyjmujemy 2



1

=

A

S1

b

w

⋅

d

=

156

100⋅6

=

2,6⋅10

−

3

f

ck

=

20 MPa=2

kN

cm

2

k

1

=

0,15



cp

=

N

Ed

A

c

=

0

b

w

=

100cm

b=6cm

V

Rd , c

=

0,12⋅2⋅100⋅2,6⋅10

−

3

⋅

2



1
3



⋅

100⋅6=115,8 kN

V

Rd , c

=

115,8 kN V

Ed

=

14,64 kN ⇒element nie wymaga dodatkwego zbrojenia na ścinanie

ŻEBRO

Zestawienie obciążeń zmiennych:

P

K

=

6

kN

m

2

⋅

2 m=12

kN

m

P

O

=

9⋅2=18

kN

m

M

Ed

=

a⋅g

o

⋅

l

eff

2



b⋅P

o

⋅

l

eff

2

V

Ed

=⋅

g

o

⋅

l

eff

⋅

P

o

⋅

l

eff

rodzaj warstwy

obciążenie charakterystyczne

współczynnik obliczeniowy

obciążenie obliczeniowe
go (kN/m)

płyta

6,77

1,35

9,140

ciężar własny żebra

1,6

1,35

2,160

ciężar tynku

0,02

1,35

0,031

suma

Go=11,33 kN/m

gk( kN/ m)

gk= 3,385 * l(płyty)

0,08*(h-hf)*25

Gk= 8,4 kN/m

A

B

C

D

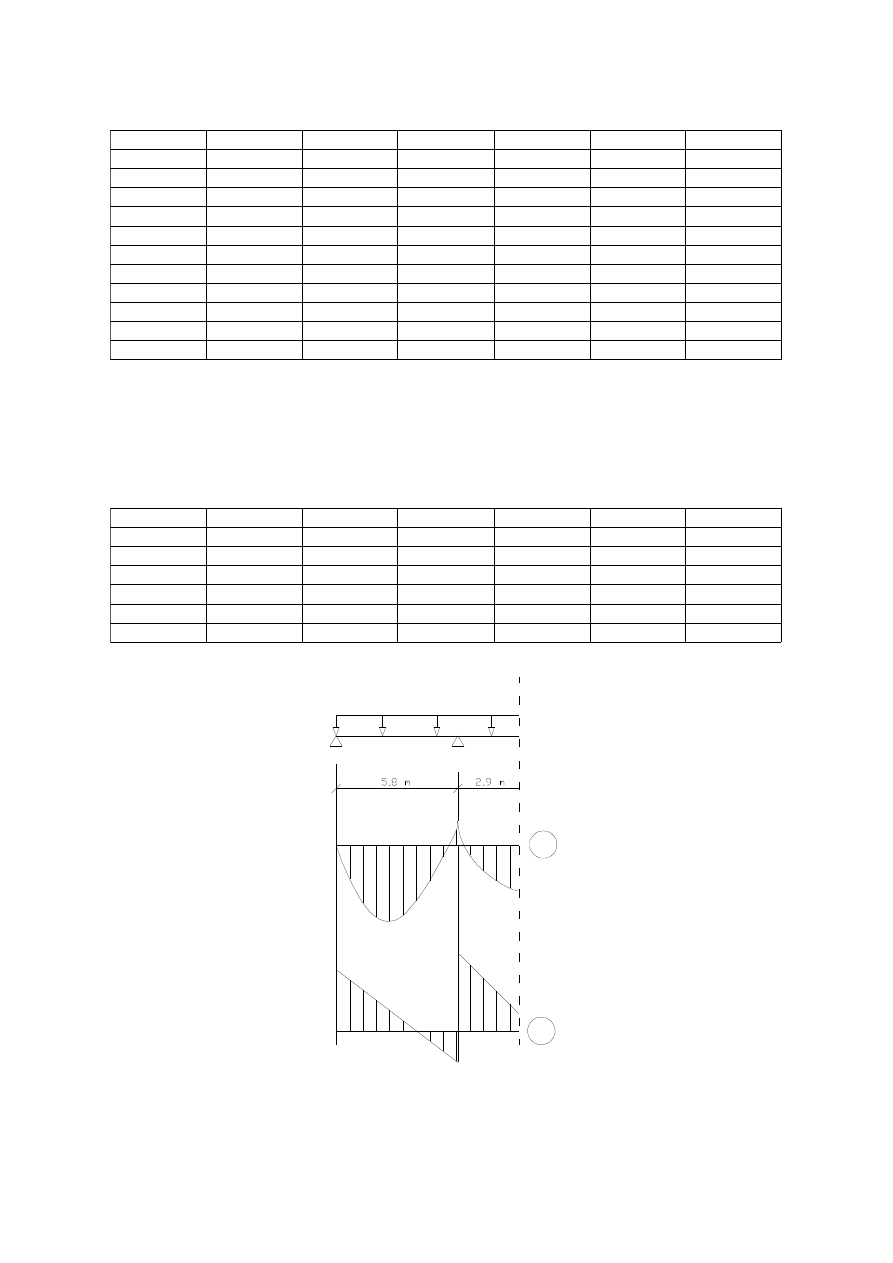
M

Q

91,04

54,94

28,02

93,75

20,66

-37,68

73,27

Przęsło skrajne:

x/l

a

b

α

β

M

V

0,0

0,000

0,000

0,4

0,4500

0,00

73,27

0,1

0,035

0,040

0,3

0,3560

37,56

56,88

0,2

0,060

0,070

0,2

0,2752

65,25

41,87

0,3

0,075

0,090

0,1

0,2065

83,08

28,13

0,4

0,080

0,100

0,0

0,1496

91,04

15,62

0,5

0,075

0,100

-0,1

0,1042

89,14

4,31

0,6

0,060

0,090

-0,2

0,0694

77,37

-5,90

0,7

0,035

0,070

-0,3

0,0443

55,73

-15,09

0,8

0,000

0,04022

-0,4

0,0280

24,35

-23,36

0,9

-0,045

0,02042

-0,5

0,0193

-4,79

-30,84

1,0

-0,100

0,01667

-0,6

0,0167

-28,02

-37,68

11,330

18,000

5,800

Przęsło przyskrajne:

x/l

a

b

α

β

M

V

0,0

-0,100

0,01667

0,5

0,5833

-28,02

93,75

0,1

-0,055

0,01514

0,4

0,4870

-11,80

77,13

0,2

0,000

0,05000

0,3

0,3991

30,28

61,38

0,3

0,005

0,05500

0,2

0,3210

35,21

46,66

0,4

0,020

0,07000

0,1

0,2537

50,01

33,06

0,5

0,025

0,07500

0,0

0,1979

54,94

20,66

g

0

P

0

l

eff

WYMIAROWANIE NA ZGINANIE

a

1

= 4 cm

Dobór materiałów:

•

beton C20/25,

f

ck

=

20 MPa

f

cd

=

13,3 MPa

f

ctm

=

2,2 MPa

E

cm

=

30 GPa

f

ctk

=

1,5 MPa

•

stal SPB B500

f

yd

=

420 MPa

f

yk

=

500 MPa

E

s

=

200 GPa

•



efflim

=

0,5



strzem

=

8 mm

c

strzem

=

30 mm

c

zbroj.gł

=

40 mm

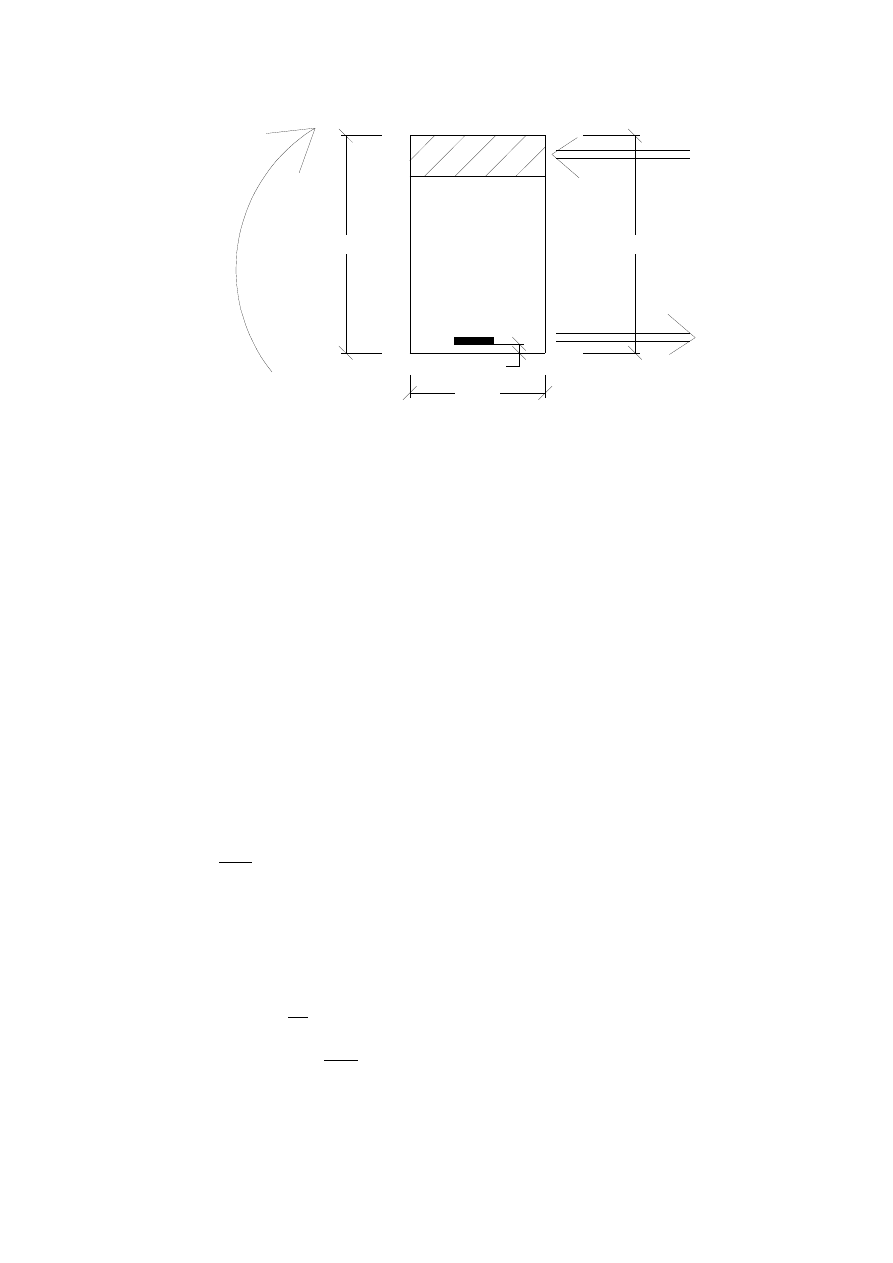
b

eff ,i

=

0,2 b

i



0,1 l

0

b

eff ,i

=

0,2⋅5,8−

0,15

2



0,1⋅0,85⋅5,8=1,06 m

b

eff

=

b

eff ,i



b

ż

b

eff

=

1,060,15=1,21 m

Sprawdzenie czy przekrój jest pozornie teowy:

M

hf

=

cc

⋅

b

eff

⋅

h

f

⋅

f

cd

⋅

d −

h

f

2



M

hf

=

1⋅1,21⋅0,08⋅13,3⋅0,36−

0,08
2

=

0,178 MNm=180 kNm

M

hf

=

180 kNm  M

Ed

=

91,04 kNm ⇒ przekrój wymiarujemy jako h x b

eff

d

40

b=15

a1

x

eff

*b*f

cd

A

s1

*f

yd

A

s1

M

Ed

A

S1

=

M

Ed

f

yd

⋅

d −

x

eff

2



=

0,091

420⋅0,36−

0,016

2



=

6,16 cm

2

przyjęto 4 14 o A

S1

=

6,16 cm

2

Podpora B

M

Ed

=

28,02 kNm=0,028 MNm

d =h−a

1

⇒

d =40−4=36cm



M

AS1

=

0⇒ x

eff

⋅

b

ż

⋅

f

cd

⋅

d −

x

eff

2

−

M

Ed

=

0

x

eff

⋅

0,15⋅13,3⋅0,36−

x

eff

2

−

0,028=0

−

0,998⋅x

eff

2



0,718⋅x

eff

−

0,028=0

=

0,718

2

−

4⋅−0,998⋅−0,028=0,404



=

0,636

x

eff1

=

−

0,718−0,636

−

2⋅0,998

=

0,68 m0,40 m

x

eff2

=

−

0,7180,636

−

2⋅0,998

=

0,041 m

0,041

0,36

=

0,110,5 ⇒ zbrojenie pojedyncze

A

S1

=

M

Ed

f

cd

⋅

d −

x

eff

2



=

0,028

420⋅0,36−

0,041

2



=

1,96 cm

2

przyjęto 4  8 o A

S1

=

2,01 cm

2

M

Ed

=

91,04 kNm=0,091 MNm

d =h−a

1

⇒

d =40−4=36cm



M

AS1

=

0 ⇒ x

eff

⋅

b

eff

⋅

f

cd

⋅

b−

x

eff

2

−

M

Ed

=

0

x

eff

⋅

1,21⋅13,3⋅0,36−

x

eff

2

−

0,091=0

−

8,05⋅x

eff

2



5,79⋅x

eff

−

0,091=0

=

5,79

2

−

4⋅−8,05⋅−0,091=30,59



=

5,53

x

eff1

=

−

5,79−5,53

−

2⋅8,05

=

0,7 m0,4 m x

eff2

=

−

5,795,53

−

2⋅8,05

=

0,016 m

0,016

0,36

=

0,0440,5⇒ zbrojenie pojedyncze

WYMIAROWANIE NA ŚCINANIE

V

Rd , c

=[

C

Rd.C

⋅

k⋅100⋅

L

⋅

f

ck





1
3





k

1

⋅

cp

]⋅

b

w

⋅

d

C

Rd , c

=

0.18

A

c

=

0.18
1.5

=

0.12

k

1

=

0.15

k =1



200
d

=

1



200

360

=

1.75



L

=

A

s1

b

w

⋅

d

=

1.96
15⋅36

=

3,6⋅10

−

3

f

ck

=

20

MN
m

2



cp

=

N

Ed

A

c

=

0

b

w

=

0,15 m d =0,37 m

V

Rd , C

=[

0.12⋅1.75⋅100⋅0,0036⋅20

 1

3





0.15⋅0]⋅0,15⋅0,36=0,0219 MN =21,9 kN V

Ed

=

88.61 kN

lecz nie mniej niż :
V

Rd , c

=

min



k

1



cp



b

w

d



min

=

0,035⋅k

3
2

⋅

f

ck

1

2

=

0,035⋅1,75

3
2

⋅

20

1
2

=

0,362

V

Rd , c

=

0,362⋅0,15⋅0,36=0,020 MN =20 kN

V Rd , c=21,9 kN

Siła poprzeczna na odcinkach nie wymagających zbrojenia na ścinanie musi zawsze spełniać
warunek:

V

Ed



0,5⋅b

w

⋅⋅

f

cd

=

0,61−

f

ck

250



=

0,6

1−20

250

=

0,55

0,5⋅0,15⋅0,37⋅0,55⋅13,3=0,203 MN =203 kN  V

Ed

Odcinki wymagające zbrojenie na ścinanie:

V

Rd , max

=



cw

⋅

b

w

⋅

z⋅

1

⋅

f

cd



cot tan 



cw

=

1,0

z =0,9 d =0,36⋅0,9=0,32

cot =1.5

tan =0.67



1

=

0.6⋅1−

f

ck

250

=

0.6⋅1−

20
250

=

0.55

V

Rd , max

=

1⋅0,15⋅0,32⋅0,55⋅13,3



1,50,67

=

0,162 MN =162 kN

V

Rd , max

=

162 kN  V

Ed

=

93,75 kN ⇒

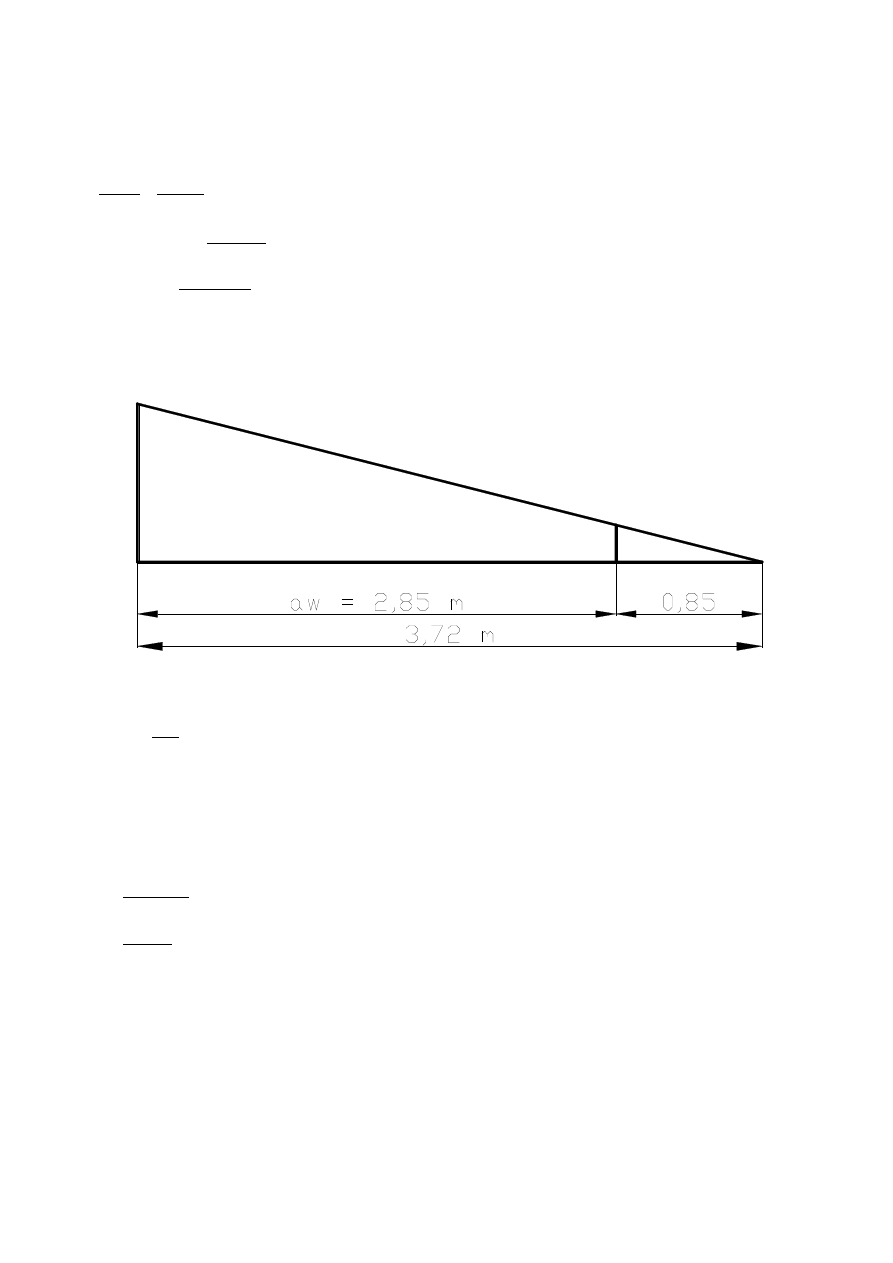
Wymiary przekroju poprzecznego belki dobrano prawidłowo.

l

n

=

3,72 m

V

Ed

V

Rd , c

=

l

n

l

n

−

a

w

a

w

=

l

n

−

l

n

⋅

V

Rd , c

V

Ed

a

w

=

3,72−

3,72⋅21,9

93,75

=

2,85 m

V

Rd , s

=

A

sw

s

⋅

z⋅f

ywd

⋅

cot 

Przyjęto strzemiona dwucięte 8mm ze stali klasy C ⇒ f

ywd

=

420MPa

A

sw

=

2⋅a

sw

=

1 cm

2

Rozstaw strzemion s

1

określamy ze wzoru :

s≤

A

sw

⋅

f

ywd

V

Ed

⋅

z⋅cot 

s≤

1,0⋅42
93,75

⋅

32⋅1,5

s≤21,5 cm  przyjęto s=20 cm

RYSY

–

C20/25

–

XC1

–

f

ck

=20 MPa

–

f

cd

= 13.3 MPa

V

Ed

=

93,75 kN

V

Rd,c

= 21,9 kN

w

k

=

S

r , max

⋅

sm

−

cm





sm

−

cm

=



s

⋅

k

t

⋅

f

ct ,eff



p , eff

⋅

1

e

⋅

p ,eff



E

s



0.6⋅

s

E

s



s

=

M

Ed



d

⋅

d⋅A

s1



s

=

9104kNcm
0.8⋅36 cm⋅6,16

2

=

51,32

kN
cm

2

k

t

=

0.4



e

=

E

s

E

cm

=

200

30

=

6.67

f

ct , eff

=

f

ctm

=

2.2 MPa



d

=

0.9
0.85
0.8

gdy



0.5 %

0.5 

p



1 %



p



1 %



p

=

A

S1

b⋅d

=

6,16 cm

2

36 cm⋅15 cm

=

0.011=1,1 %⇒ 

d

=

0.8



p , eff

=

A

S1

A

c ,eff

A

c , eff

=

2.5⋅70−66=10



p , eff

=

6,16
10

=

0,62



sm

−

cm

=



s

⋅

k

t

⋅

f

ct ,eff



p , eff

⋅

1

e

⋅

p ,eff



E

s

=

51,32⋅0.4⋅

0.22

0,62

⋅

16.67⋅0,62

20500

=

0,0018

0.6⋅

s

E

s

=

0.6⋅51,32
20500

=

0,0015  0,0018

S

r , max

=

k

3

⋅

ck

1

⋅

k

2

⋅

k

4

⋅




p , eff

k

1

=

0.8

k

2

=

0.5

k

3

=

3.4

k

4

=

0.425

c=3 cm

S

r , max

=

3.4⋅30.8⋅0.5⋅0.425⋅

6,16
0,62

=

11,89 cm

w

k

=

S

r , max

⋅

sm

−

cm

=

11,89⋅0,0018=0,021 cm=0,21 mm0.4 mm

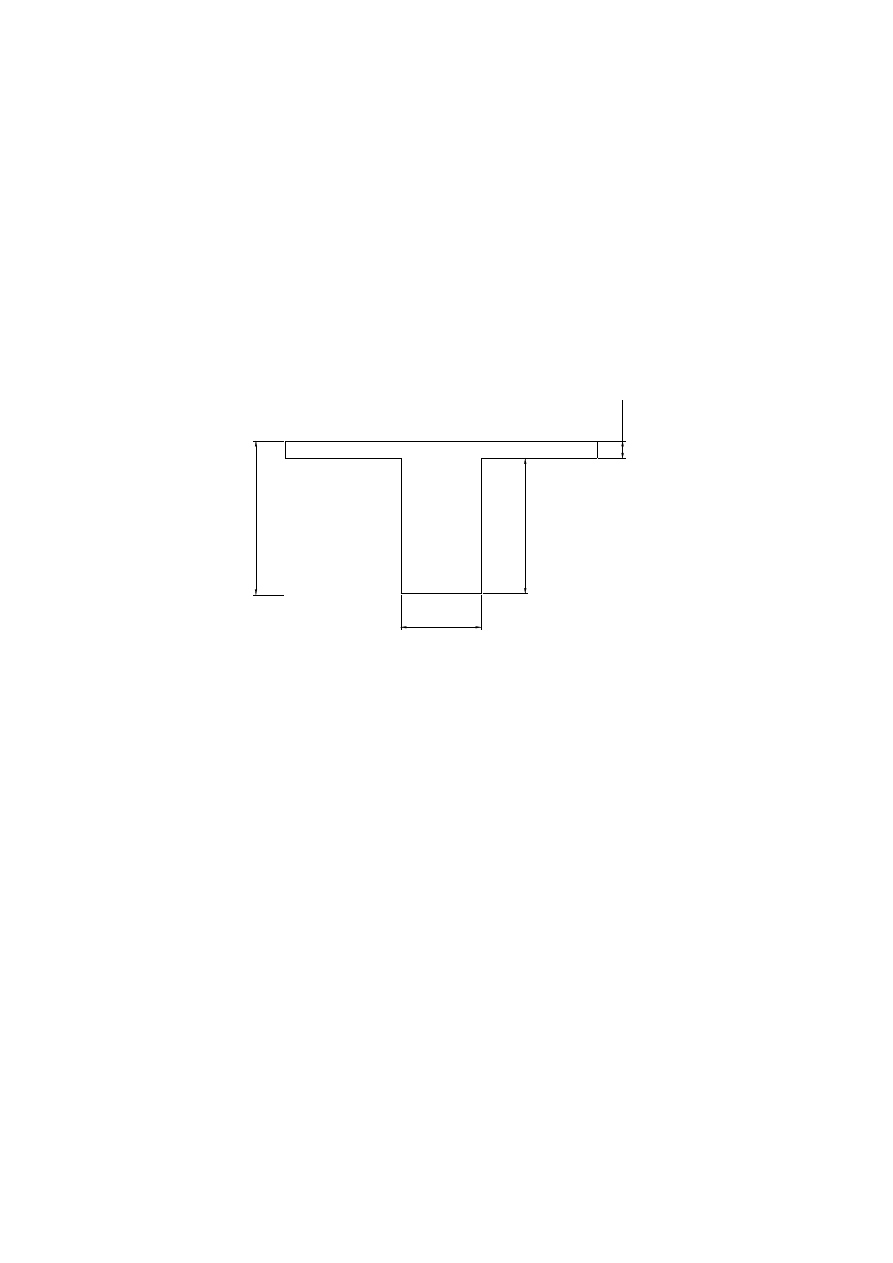
PODCIĄG

Zestawienie obciążeń:

V

Ed

=−

0,6⋅11,33⋅5,80,0167⋅18⋅5,8=−37,68 kN

V

Ed

=

0,5⋅11,33⋅5,80,5833⋅18⋅5,8=93,75 kN

-obciążenia stałe:

G=0,6⋅11,33⋅5,80,5⋅11,33⋅5,8=72,29 kN

-obciążenia zmienne

P=0,0167⋅18⋅5,80,5833⋅18⋅5,8=62,64 kN

Q

i

=

a⋅Gb⋅P

Q

A

=

1,098⋅72,291,299⋅62,64=160,74 kN

Q

BL

=−

1,902⋅72,29−1,952⋅62,64=−259,77 kN

Q

BP

=

1,634⋅72,291,885⋅62,64=236,20 kN

Q

CL

=−

1,366⋅72,29−1,768⋅62,64=−209,50 kN

h

f=

0

,0

8

m

0

,6

2

b=0,35m

h

=

0

,7

m

M

i

=

a⋅G⋅l

eff



b⋅P⋅l

eff

Q=a⋅q

o



b⋅P

o

M

1

=

0.299⋅72,29⋅60.400⋅62,64⋅6=280,02 kNm

M

2

=

0.165⋅72,29⋅60.333⋅62,64⋅6=196,72 kNm

M

B

=−

0.402⋅72,29⋅6−0.452⋅62,64⋅6=−344,24 kNm

M

C

=−

0.268⋅72,29⋅6−0.402⋅62,64⋅6=−267,33 kNm

Dobór materiałów:

•

beton C20/25,

f

ck

=

20 MPa

f

cd

=

13,3 MPa

f

ctm

=

2,2 MPa

E

cm

=

30 GPa

f

ctk

=

1,5 MPa

•

stal SPB B500

f

yd

=

420 MPa

f

yk

=

500 MPa

E

s

=

200 GPa

•



efflim

=

0,5



strzem

=

8 mm

c

strzem

=

30 mm

c

zbroj.gł

=

40 mm

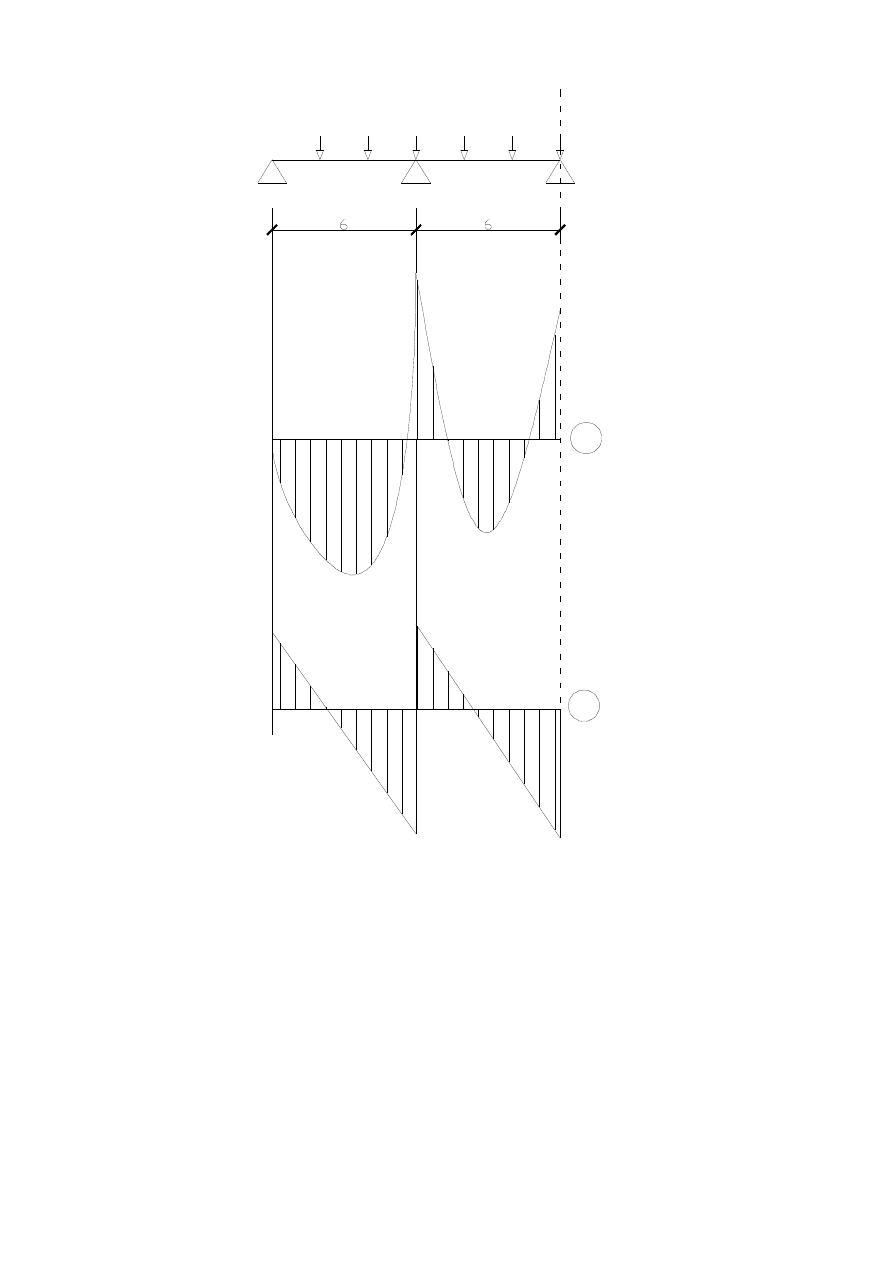
A

B

C

G +P

G +P

G +P

G +P

G +P

G +P

280,02

196,72

344,24

267,33

M

Q

160,74

236,20

259,77

209,50

Podpora B

M

Ed

=

344,24 kNm=0,344 MNm

f

cd

⋅

b⋅x

eff

⋅

d −

x

eff

2

−

M

Ed

=

0

1⋅13,3⋅0,35⋅x

eff

⋅

0,67−

x

eff

2

−

0,344=0

−

2,33 x

eff

2



3,12 x

eff

−

0,344=0

=

6,53⇒



=

2,56

x

eff1

=

0,910,70 m

x

eff2

=

0,09 m



eff

=

9
67

=

0.130.5



M

Acc

=

0

A

S1

⋅

f

yd

⋅

d −

x

eff

2

−

M

Ed

=

0

A

S1

=

M

Ed

f

yd

⋅

d −

x

eff

2



=

0,344

420⋅0,67−

0,09
2



=

31,09 cm

2

przymmuje 4  22 o A

s1

=

13,1 cm

2

Przęsło I

b

eff ,i

=

0,2 b

i



0,1 l

0

b

eff ,i

=

0,2⋅3−

0,35

2



0,1⋅0,85⋅6=1,08 m

b

eff

=

b

eff ,i



b

ż

b

eff

=

1,080,35=1,43 m

M

Ed

=

280 kNm=0,280 MNm

h

f

=

8cm

h

p

=

0.7m=70 cm

b

p

=

0.35 m=35 cm

d =h

p

−

a

1

⇒

d =70−4=66cm

M

hf

=

0,08⋅1,43⋅13,3⋅0,66−

0,08

2

=

0,943 MNm=943kNmM

Ed

=

280 kNm⇒

przekrój

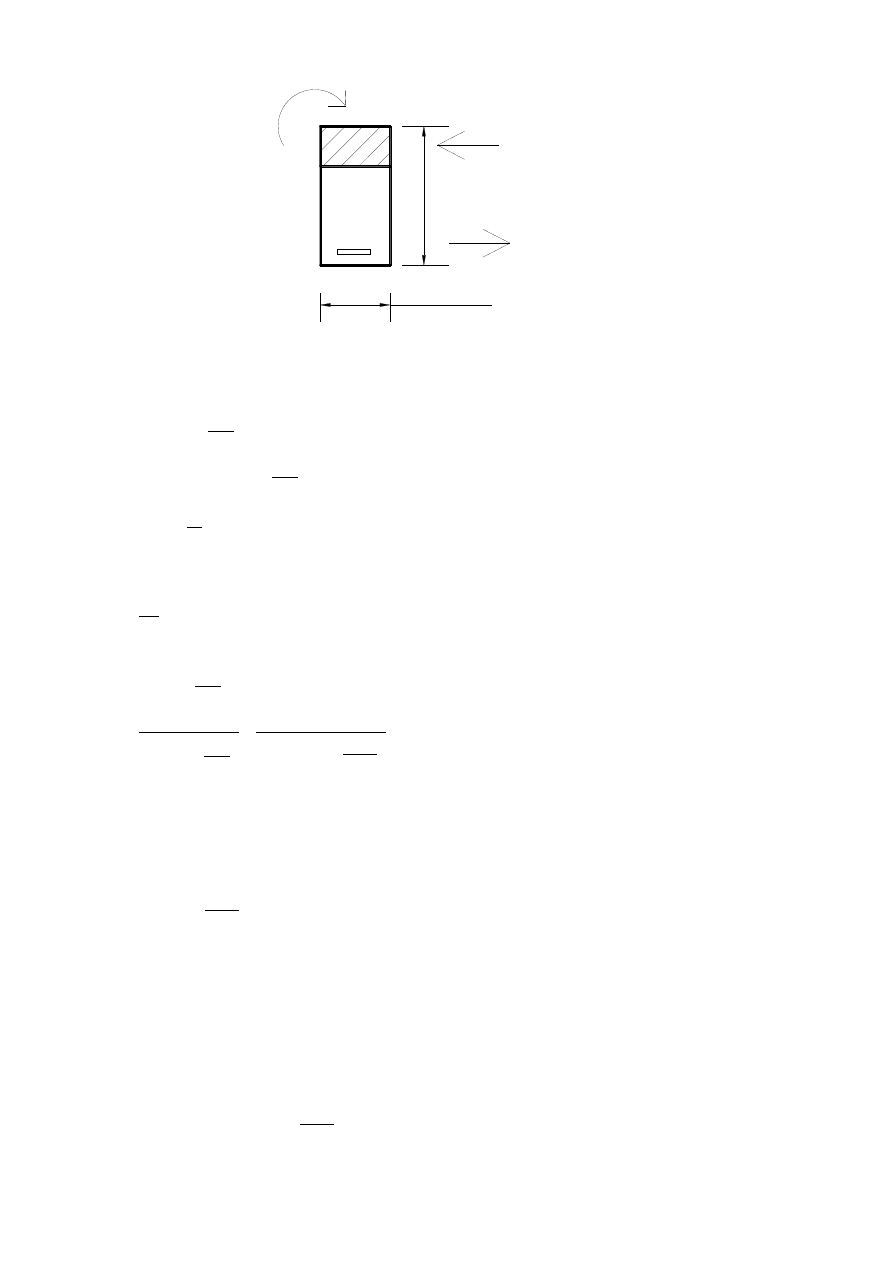
pozornie teowy

hp

=

0

.7

m

beff=1.85m

A

cc

*f

cd

A

s1

*f

yd

M

Ed

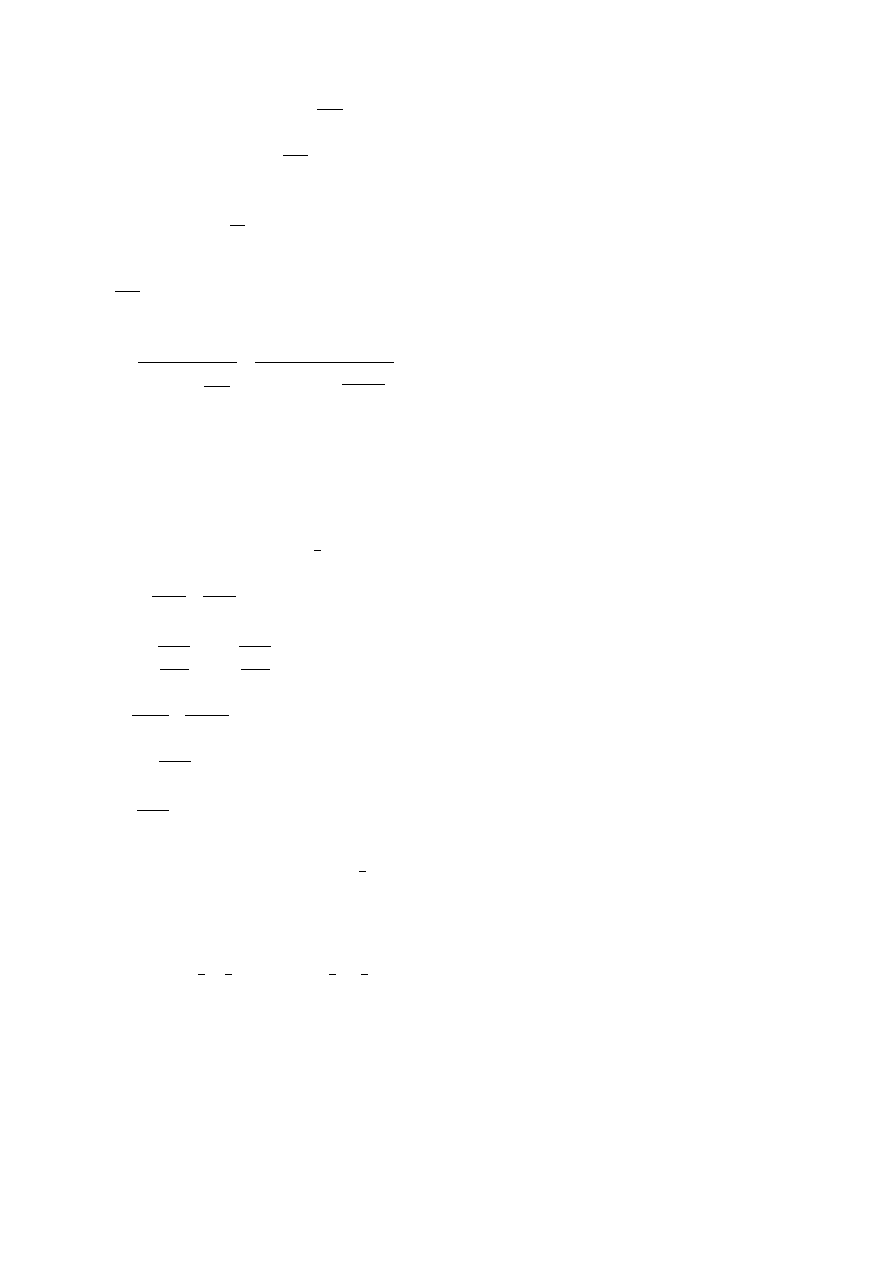
A

S1

=

M

Ed

f

cd

⋅

d −

x

eff

2



=

0,280

420⋅0,66−

0,023

2



=

10,28 cm

2

przymmuje 4 20 o A

s1

=

12,56 cm

2

WYMIAROWANIE NA ŚCINANIE

V

Rd , c

=[

C

Rd.C

⋅

k⋅100⋅

L

⋅

f

ck





1
3





k

1

⋅

cp

]⋅

b

w

⋅

d

C

Rd , c

=

0.18

A

c

=

0.18
1.5

=

0.12

k

1

=

0.15

k =1



200
d

=

1



200

660

=

1.55



L

=

A

s1

b

w

⋅

d

=

12,56
35⋅66

=

0,0054

f

ck

=

20

MN
m

2



cp

=

N

Ed

A

c

=

0

b

w

=

0,35 m d =0,66 m

V

Rd , C

=[

0.12⋅1.55⋅100⋅0,0054⋅20



1
3





0.15⋅0]⋅0,35⋅0,66=0,095 MN =95 kN V

Ed

=

260 kN

lecz nie mniej niż :
V

Rd , c

=

min



k

1



cp



b

w

d



min

=

0,035⋅k

3
2

⋅

f

ck

1

2

=

0,035⋅1,55

3
2

⋅

20

1
2

=

0,302

V

Rd , c

=

0,302⋅0,35⋅0,66=0,070 MN =70 kN

V Rd , c=95 kN



M

AS1

=

0⇒ x

eff

⋅

b

eff

⋅

f

cd

⋅

d −

x

eff

2

−

M

Ed

=

0

x

eff

⋅

1,43⋅13,3⋅0,66−

x

eff

2

−

0,280=0

−

9,51⋅x

eff

2



12,55⋅x

eff

−

0,280=0

=

146,85



=

12,12

x

eff1

=

1,30h

f

=

0,08 x

eff2

=

0,023 m

2,3

66

=

0.0350,5⇒ zbrojenie pojedyncze

Siła poprzeczna na odcinkach nie wymagających zbrojenia na ścinanie musi zawsze spełniać
warunek:

V

Ed



0,5⋅b

w

⋅⋅

f

cd

=

0,61−

f

ck

250



=

0,6

1−20

250

=

0,55

0,5⋅0,35⋅0,66⋅0,55⋅13,3=1,536 MN =1536 kN  V

Ed

Odcinki wymagające zbrojenie na ścinanie:

V

Rd , max

=



cw

⋅

b

w

⋅

z⋅

1

⋅

f

cd



cot tan 



cw

=

1,0

z =0,9 d =0,66⋅0,9=0,60

cot =1.5

tan =0.67



1

=

0.6⋅1−

f

ck

250

=

0.6⋅1−

20
250

=

0.55

V

Rd , max

=

1⋅0,35⋅0,60⋅0,55⋅13,3



1,50,67

=

0,708 MN =708 kN

V

Rd , max

=

708 kN  V

Ed

=

269 kN ⇒

Wymiary przekroju poprzecznego belki dobrano prawidłowo.

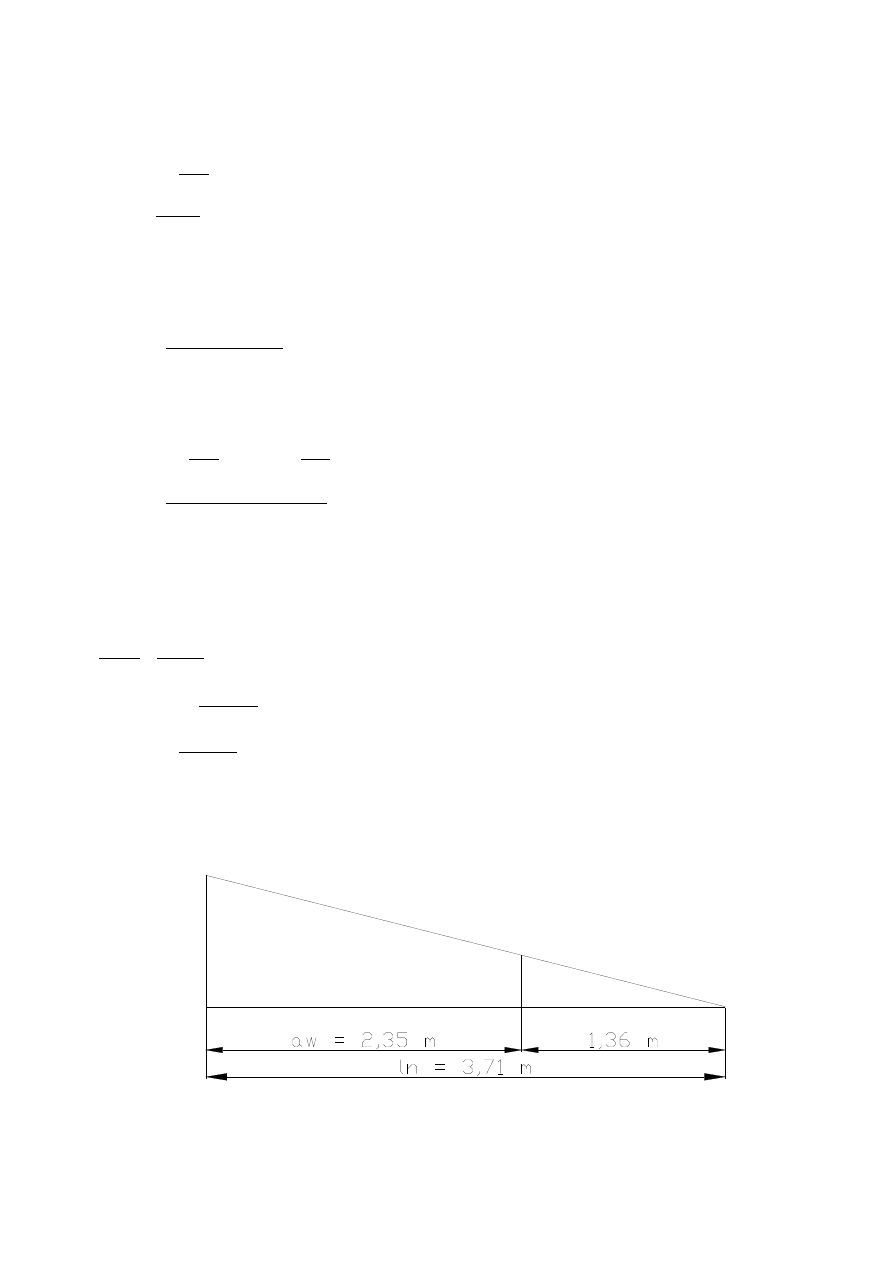
l

n

=

3,71 m

V

Ed

V

Rd , c

=

l

n

l

n

−

a

w

a

w

=

l

n

−

l

n

⋅

V

Rd ,c

V

Ed

a

w

=

3,71−

3,71⋅95

260

=

2,35 m

V

Ed

=

260kN

V

Rd,c

= 95 kN

V

Rd , s

=

A

sw

s

⋅

z⋅f

ywd

⋅

cot 

Przyjęto strzemiona dwucięte 8mm ze stali klasy C ⇒ f

ywd

=

420MPa

A

sw

=

2⋅a

sw

=

1 cm

2

Rozstaw strzemion s

1

określamy ze wzoru :

s≤

A

sw

⋅

f

ywd

V

Ed

⋅

z⋅cot 

s≤

1,0⋅42
260

⋅

60⋅1,5

s≤14,54 cm przyjęto s=14 cm

RYSY

–

C20/25

–

XC1

–

f

ck

=20 MPa

–

f

cd

= 13.3 MPa

w

k

=

S

r , max

⋅

sm

−

cm





sm

−

cm

=



s

⋅

k

t

⋅

f

ct ,eff



p , eff

⋅

1

e

⋅

p ,eff



E

s



0.6⋅

s

E

s



s

=

M

Ed



d

⋅

d⋅A

s1



s

=

28000kNcm

0.85⋅70 cm⋅13,1 cm

2

=

35,92

kN
cm

2

k

t

=

0.4



e

=

E

s

E

cm

=

200

30

=

6.67

f

ct , eff

=

f

ctm

=

2.2 MPa



d

=

0.9
0.85
0.8

gdy



0.5 %

0.5 

p



1 %



p



1 %



p

=

A

S1

b⋅d

=

13,1 cm

2

70 cm⋅35 cm

=

0.005=0,5 %⇒ gp

d

=

0.85



p , eff

=

A

S1

A

c ,eff

A

c , eff

=

2.5⋅70−66=10



p , eff

=

13,1
10

=

1,31



sm

−

cm

=



s

⋅

k

t

⋅

f

ct ,eff



p , eff

⋅

1

e

⋅

p ,eff



E

s

=

35,92⋅0.4⋅

0.22

1,31

⋅

16.67⋅1,31

20500

=

0,0011

0.6⋅

s

E

s

=

0.6⋅35,92
20500

=

0,0011  0,0011

S

r , max

=

k

3

⋅

ck

1

⋅

k

2

⋅

k

4

⋅




p , eff

k

1

=

0.8

k

2

=

0.5

k

3

=

3.4

k

4

=

0.425

c=3 cm

S

r , max

=

3.4⋅30.8⋅0.5⋅0.425⋅

13,1
1,31

=

11,90 cm

w

k

=

S

r , max

⋅

sm

−

cm

=

11,9⋅0,0011=0,013 cm=0,18 mm0.4 mm