TEMAT ĆWICZENIA
Wyznaczanie zależności temperatury wrzenia wody od ciśnienia
CEL ĆWICZENIA
Głównym celem ćwiczenia jest wyznaczenie zależności temperatury wrzenia wody od
ciśnienia.
PODSTAWY TEORETYCZNE DO SAMODZIELNEGO OPRACOWANIA
Para nasycona sucha i para mokra, para przegrzana, stopień suchości, utajone ciepło
parowania (utajona entalpia parowania), zależność ciśnienia pary wodnej nasyconej od
temperatury, wykres stanów dla wody w układach współrzędnych p-v, T-s, h-s, punkt
potrójny wody, punkt krytyczny wody, równanie Clausiusa-Clapeyrona, równanie Antoine'a,
metoda najmniejszych kwadratów.
ZESTAW POMIAROWY
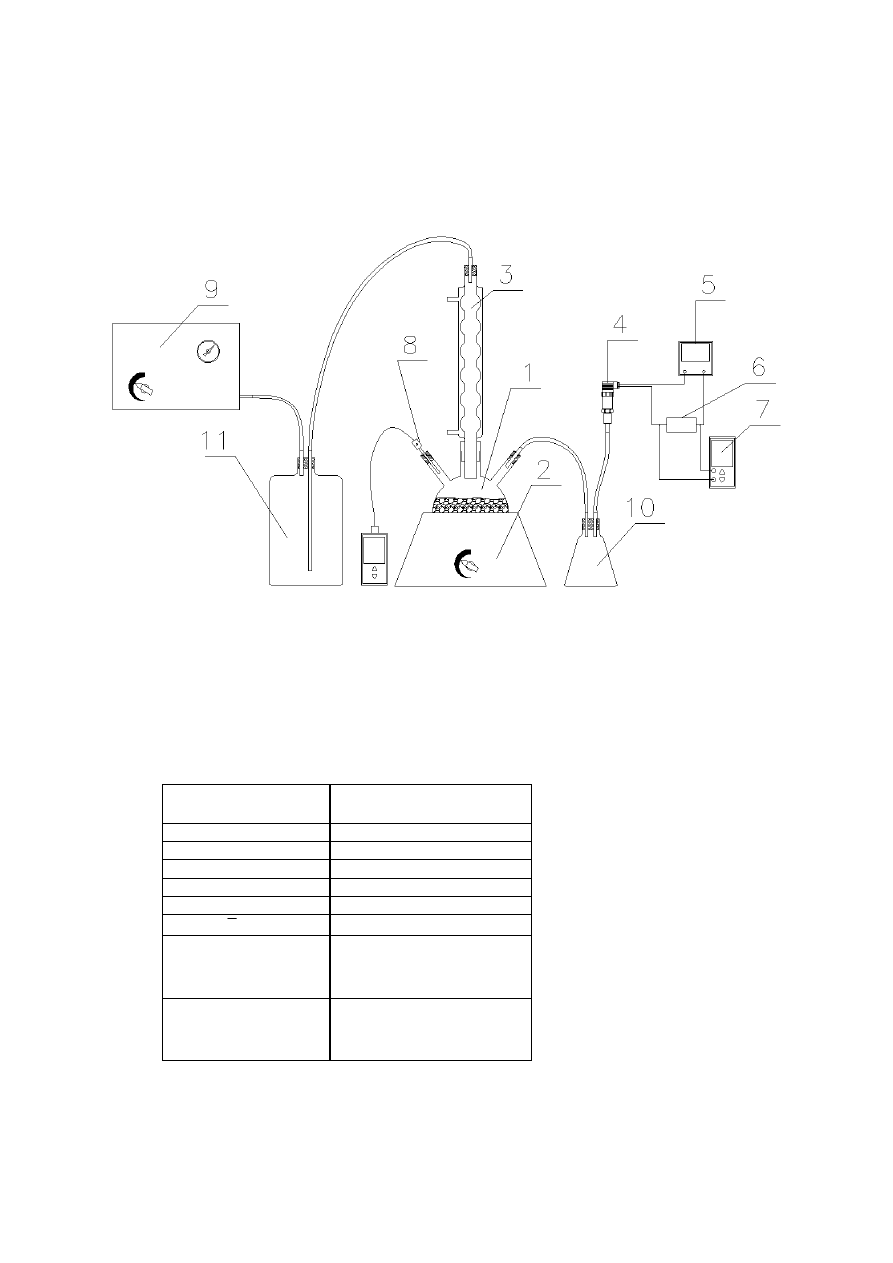
Przedstawiony na rys.1 zestaw pomiarowy składa się z membranowej pompy próżniowej o
regulowanej mocy ssania 9, dzięki której jest możliwe uzyskanie podciśnienia nad
powierzchnią wody znajdującą się w szklanej kolbie 1. Do ogrzewania wody znajdującej się
w kolbie wykorzystywana jest czasza grzejna o regulowanej mocy grzewczej 2. Wytworzona
w kolbie para wodna jest skraplana w szklanej chłodnicy wodnej 3.
Pomiar temperatury pary znajdującej się w kolbie jest realizowany za pomocą
rezystancyjnego czujnika temperatury 8 (Pt100) pracującego w układzie trójprzewodowym o
rezystorze pomiarowym wykonanym w klasie B wg PN - EN 60751 + A2: 1997 (dla klasy B
niepewność pomiaru temperatury wyrażonej w
o
C jest równa
(
)
T
,
,
⋅
+
±
005
0
3
0
). Odczyt
temperatury odbywa się za pomocą przenośnego miernika o temperatury o zakresie
pomiarowym −50÷200
o
C i niepewności pomiaru ±(0,15%zakresu + 1dgt). Do pomiaru zmian
ciśnienia pary wodnej zastosowano przetwornik ciśnienia 4 o zakresie pomiarowym −1÷0,6
bar z prądowym sygnałem wyjściowym (4÷20 mA) i liniowej charakterystyce. Dopuszczalna
temperatura pomiaru ciśnienia dla tego przetwornika wynosi 80
o
C. Niepewność pomiarowa
przetwornika wynosi 0,25% zakresu pomiarowego. Przetwornik jest zasilany przy pomocy
stabilizowanego zasilacza prądu stałego 5. Pomiar ciśnienia w kolbie odbywa się na
podstawie pomiaru spadku napięcia na rezystorze 6 o znanej rezystancji R, przy pomocy
cyfrowego woltomierza 7 o niepewności pomiaru napięcia DC ±(0,5% wartości zmierzonej+
2dgt).
Do pomiaru ciśnienia barometrycznego zastosowano rtęciowy barometr stacyjny.
W cylindrze 11 znajduje się substancja osuszająca (sito molekularne). Naczynie 10
stanowi rodzaj buforu zabezpieczającego przetwornik ciśnienia.
PROCEDURA POMIAROWA
Przed uruchomieniem stanowiska należy sprawdzić szczelność wszystkich połączeń oraz ilość
wody w kolbie. Włączyć zasilacz stabilizowany i zanotować wskazanie woltomierza 7 przy
ciśnieniu atmosferycznym panującym w kolbie. Zanotować wskazanie barometru. Następnie
włączyć zasilanie czaszy grzejnej, ustawiając jednocześnie regulator mocy grzewczej na
maksymalną moc, i podgrzać wodę do temperatury ok. 30
o
C. Zmniejszyć moc grzewczą do
ok. 50%. Włączyć przepływ wody chłodzącej przez chłodnicę. Uruchomić pompę próżniową
i ustawić maksymalną moc ssania za pomocą regulatora. Po wystąpieniu wrzenia i ustaleniu
się parametrów zanotować temperaturę wrzenia i dopowiadające jej podciśnienie dla
pierwszego punktu pomiarowego (wykonać co najmniej po pięć odczytów temperatury i
spadku napięcia ). Następnie należy zwiększyć ciśnienie nad powierzchnią wody,
zmniejszając moc ssania pompy próżniowej i ponownie doprowadzić do stanu, wrzenia cały
czas grzejąc wodę w kolbie za pomocą czaszy grzejnej. Ponownie zanotować ciśnienie i temp.
wrzenia. Procedurę powtórzyć, aż do osiągnięcia w kolbie ciśnienia atmosferycznego. Aby
wykonać, pomiar w warunkach ciśnienia atmosferycznego należy wyłączyć pompę próżniową
i wyjąc wąż z króćca ssawnego pompy. Wykonać pomiar dla co najmniej pięciu punktów
pomiarowych.
Rys.1. Schemat stanowiska pomiarowego
OPRACOWANIE WYNIKÓW POMIARÓW
Przed rozpoczęciem pomiarów należy zanotować ciśnienie atmosferyczne oraz temperaturę
panującą w laboratorium. Wykonać co najmniej pięć odczytów ciśnienia atmosferycznego.
Wyniki zestawić w tabeli 1. Obliczyć średnie z wielkości mierzonych oraz standardową
niepewność wyniku (średniej).
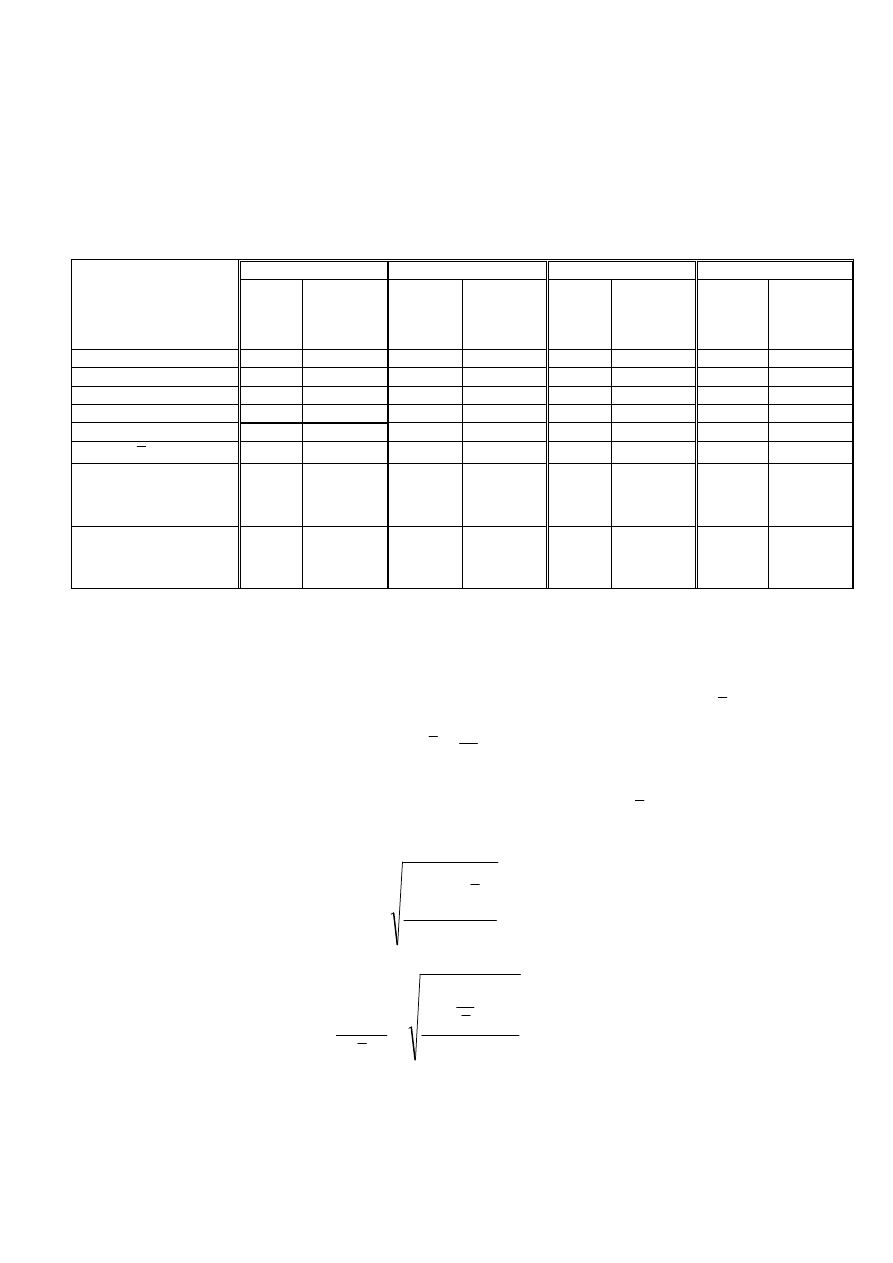
Tabela 1. Wyniki pomiarów ciśnienia atmosferycznego
W trakcie pomiaru dla każdego punktu pomiarowego (dla każdej temperatury wrzenia)
zanotować temperaturę i spadek napięcia na rezystorze pomiarowym. Wykonać co najmniej
po pięć odczytów. Wyniki zestawić w tabeli 2 przedstawionej poniżej.
L.p.
Ciśnienie atmosferyczne, p
a
mmHg
Odczyt nr 1
-/- nr 2
-/- nr 3
-/- nr 4
-/- nr 5
Średnia,
x
Niepewność
standardowa
średniej
)
p
(
u
a
A
Względna niepewność
standardowa
średniej,
)
x
(
e
A
%
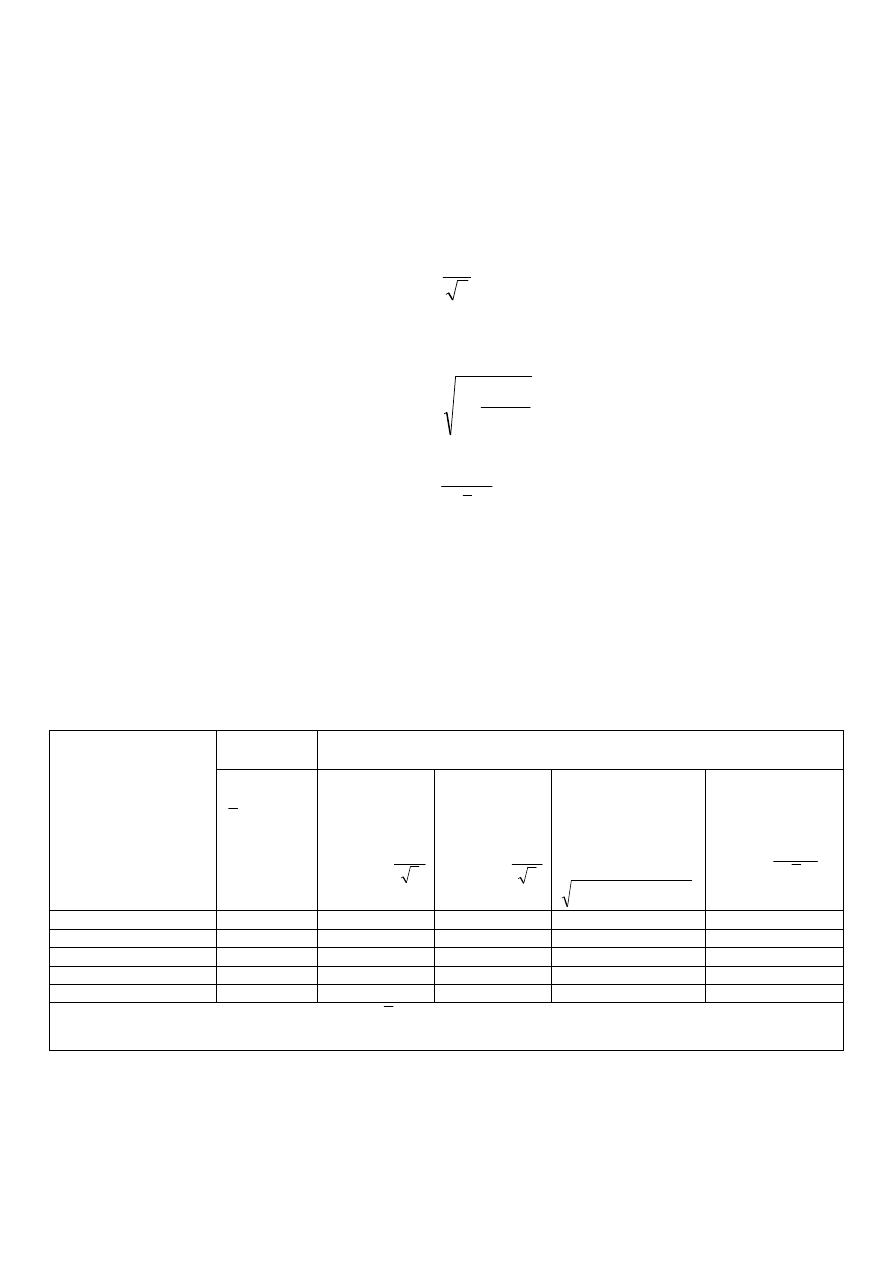
Dla każdego punktu pomiarowego obliczyć średnie z wielkości mierzonych oraz standardową
niepewność wyniku (średniej).
Tabela 2. Wyniki pomiarów ciśnienia nasycenia w funkcji temperatury.
Uwaga: Przyjąć zasadę podawania jednej cyfry znaczącej niepewności. Ostatnia cyfra
znacząca w każdym wyniku powinna być tego samego rzędu (stać na tym samym miejscu
dziesiętnym) co błąd.
Dla liczby N niezależnych pomiarów eksperymentalnej wielkości x, o jednakowych
niepewnościach, najbardziej wiarygodnym przybliżeniem jest średnia arytmetyczna
x
∑
=
⋅
=
N
i
i
x
N
x
1
1
,
(1)
gdzie : N -liczba pomiarów.
Najlepszym przybliżeniem niepewności średniej arytmetycznej
x
jest odchylenie
standardowe średniej (jest to tzw. niepewność typu A, -jest oparta na metodzie określania
niepewności pomiaru na podstawie analizy statystycznej serii wyników pomiarów)
(
)
(
)
1
1
2
−
⋅
−
=
∑
=
N
N
x
x
)
x
(
u
N
i
i
A
,
(2)
lub operując niepewnością względną:
(
)
1
1
1
2
−
⋅
−
=
=
∑
=
N
N
x
x
x
)
x
(
u
)
x
(
e
N
i
i
A
A
.
(3)
Aby określić niepewność całkowitą pomiaru wielkości mierzonej, należy dodatkowo
uwzględnić niepewność typu B, która jest obliczana na podstawie rozkładu
prawdopodobieństwa przyjętego przez eksperymentatora. Generalnie metoda B służy do
I punkt pomiarowy
II punkt pomiarowy
i-ty punkt pomiarowy V punkt pomiarowy
Temp.
wrzenia
o
C
Spadek
napięcia na
rezystorze,
V
Temp.
wrzenia,
o
C
Spadek
napięcia na
rezystorze,
V
Temp.
wrzenia
o
C
Spadek
napięcia na
rezystorze
V
Temp.
wrzenia
o
C
Spadek
napięcia na
rezystorze
V
Odczyt nr 1
-/- nr 2
-/- nr 3
-/- nr 4
-/- nr 5
Średnia,
x
Niepewność
standardowa
średniej
)
x
(
u
A
Względna niepewność
standardowa
średniej,
)
x
(
e
A
%
szacowania niepewności instrumentalnej. Niepewność standardową typu B określa się na
drodze analizy, opartej na wszystkich możliwych informacjach.
W skład niepewności typu B wchodzą np.: niepewność wzorcowania (kalibracji) przyrządu
pomiarowego, niepewność eksperymentatora, niepewność tablicową (niepewność danych
zaczerpniętych z literatury) itp.
Przyjmuje się, że standardowa niepewność typu B jest równa odchyleniu
standardowemu rozkładu jednostajnego, czyli:
3
x
)
x
(
u
i
B
∆
=
,
(6)
gdzie:
−
x
i
∆
(błąd graniczny) np. niepewność wzorcowania przyrządu pomiarowego,
niepewność eksperymentatora, niepewność tablicowa itp.
Łączna niepewność standardowa typu B może być przedstawiona zależnością:
(
)
∑
=
i
i
B
x
)
x
(
u
3
2
∆
,
(7)
lub operując niepewnością względną:
x
)
x
(
u
)
x
(
e
B
B
=
.
(8)
Uwaga: W dokumentacji technicznej, informacje o dokładności pomiaru przyrządem
cyfrowym podawane są często w postaci uproszczonej: np. ±(0,1%+2dgt). Taki zapis należy
interpretować jako sumę błędu równego 0,1% wartości mierzonej i błędu, odpowiadającego
2-krotnej rozdzielczości pola odczytowego.
Wyniki obliczeń niepewności temperatury, napięcia i ciśnienia atmosferycznego
należy przedstawić w tabelach 3,4, i 5.
Tabela 3. Niepewność typu B pomiaru temperatury .
L.p.
Temperatura
Niepewność standardowa typu B temperatury, u
B
(T)
Średnia
arytmetyczna
T
,
o
C
Niepewność
standardowa
czujnika
temperatury,
o
C
3
T
)
T
(
u
cz
cz
B
∆
=
Niepewność
standardowa
miernika
temperatury,
o
C
3
T
)
T
(
u
m
m
B
∆
=
Łączna
niepewność
standardowa typu B
temperatury, u
B
(T)
o
C
)
T
(
u
)
T
(
u
m
cz
B
B
2
2
+
Łączna
względna
niepewność
standardowa typu B
temperatury, %
T
)
T
(
u
)
T
(
e
B
B
=
I punkt pomiarowy
II punkt pomiarowy
III punkt pomiarowy
IV punkt pomiarowy
V punkt pomiarowy
Błąd graniczny czujnika temp.:
(
)
T
,
,
T
cz
⋅
+
±
=
005
0
3
0
∆
Błąd graniczny miernika temp.:
(
)
dgt
zakresu
%
,
T
m
⋅
+
±
=
1
15
0
∆
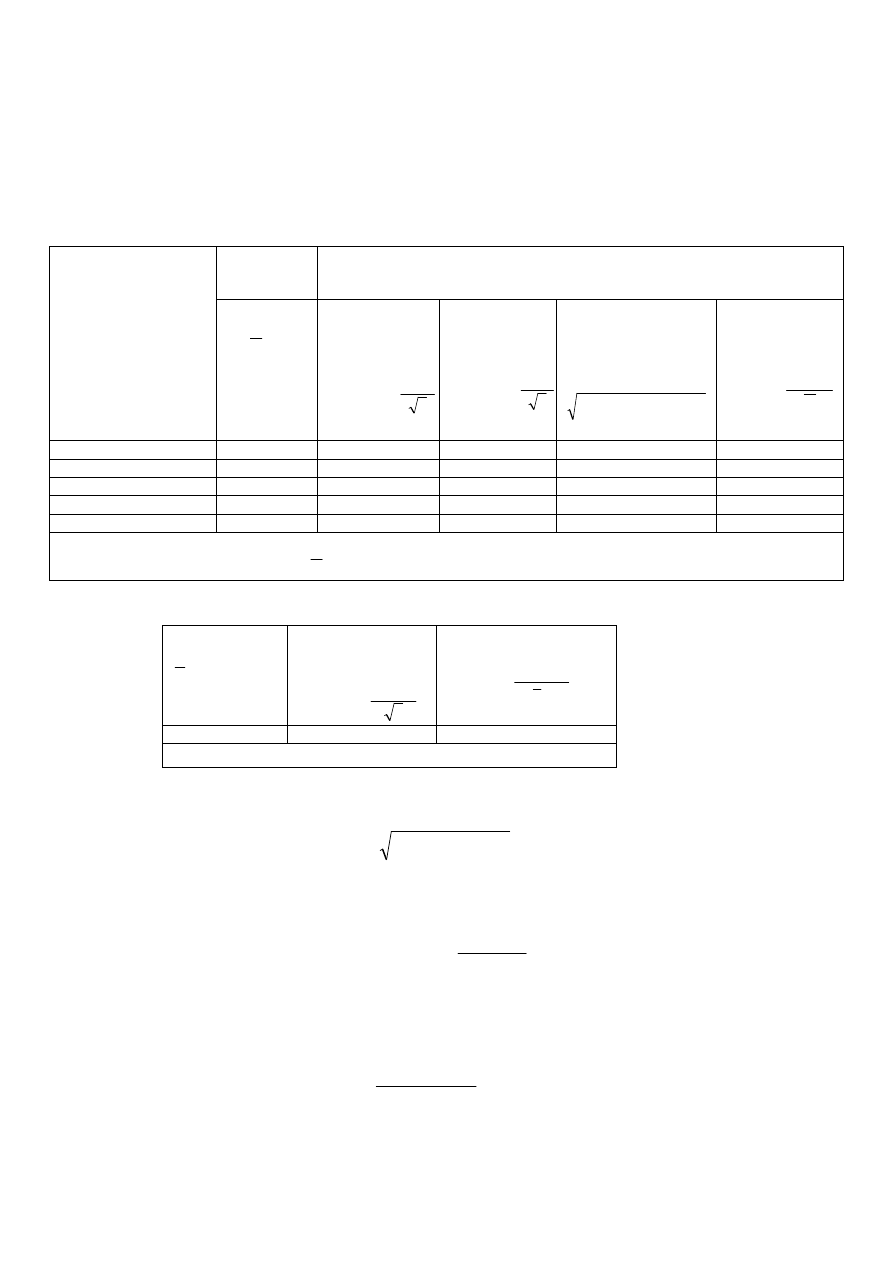
Tabela 4. Niepewność typu B pomiaru napięcia .
Tabela 5. Niepewność typu B pomiaru ciśnienia atmosferycznego
Niepewność standardowa wielkości mierzonych bezpośrednio jest sumą niepewności
standardowych typu A i typu B:
)
x
(
u
)
x
(
u
)
x
(
u
B
A
2
2
+
=
.
(9)
Aby określić ciśnienie bezwzględne jakie panuje w kolbie należy na podstawie
charakterystyki przetwornika przeliczyć wskazywane napięcie na wartość ciśnienia z
następującej zależności:
R
S
U
U
p
p
i
at
at
i
⋅
−
−
=
,
(10)
gdzie: p
at
- ciśnienie atmosferyczne, S-czułość przetwornika, U
at
-napięcie na rezystorze
odpowiadające ciśnieniu atmosferycznemu, U
i
-napięcie na rezystorze odpowiadające
podciśnieniu w kolbie w i-tym punkcie pomiarowym, R- rezystancja rezystora pomiarowego.
Dla przetwornika liniowego czułość S wyraża się zależnością:
min
max
min
max
X
X
Y
Y
S
−
−
=
, (11)
L.p.
Spadek
napięcia
na
rezystorze
Niepewność standardowa B napięcia, u
B
(V)
Średnia
arytmetyczna
U
, V
Niepewność
standardowa
przetwornika
ciśnienia,
V
3
U
)
U
(
u
cz
cz
B
∆
=
Niepewność
standardowa
miernika, V
3
U
)
U
(
u
m
m
B
∆
=
Łączna
niepewność
standardowa typu B
napięcia,
V
)
U
(
u
)
U
(
u
m
cz
B
B
2
2
+
Łączna względna
niepewność
standardowa typu
B, %
U
)
U
(
u
)
U
(
e
B
B
=
I punkt pomiarowy
II punkt pomiarowy
III punkt pomiarowy
IV punkt pomiarowy
V punkt pomiarowy
Błąd graniczny czujnika ciśnienia:
(
)
zakresu
%
,
R
S
U
cz
25
0
⋅
⋅
±
=
∆
(bez uwzględnienia niepewności rezystora)
Błąd graniczny miernika.:
(
)
dgt
U
%
,
U
m
⋅
+
±
=
2
5
0
∆
Ciśnienie
atmosferyczne,
at
p
, bar
Niepewność
standardowa średniej,
bar
3
at
cz
at
B
p
)
p
(
u
∆
=
Względna
niepewność
standardowa
średniej,
at
at
B
at
B
p
)
p
(
u
)
p
(
e
=
%
Błąd graniczny barometru.:
hPa
p
at
cz
1
±
=
∆
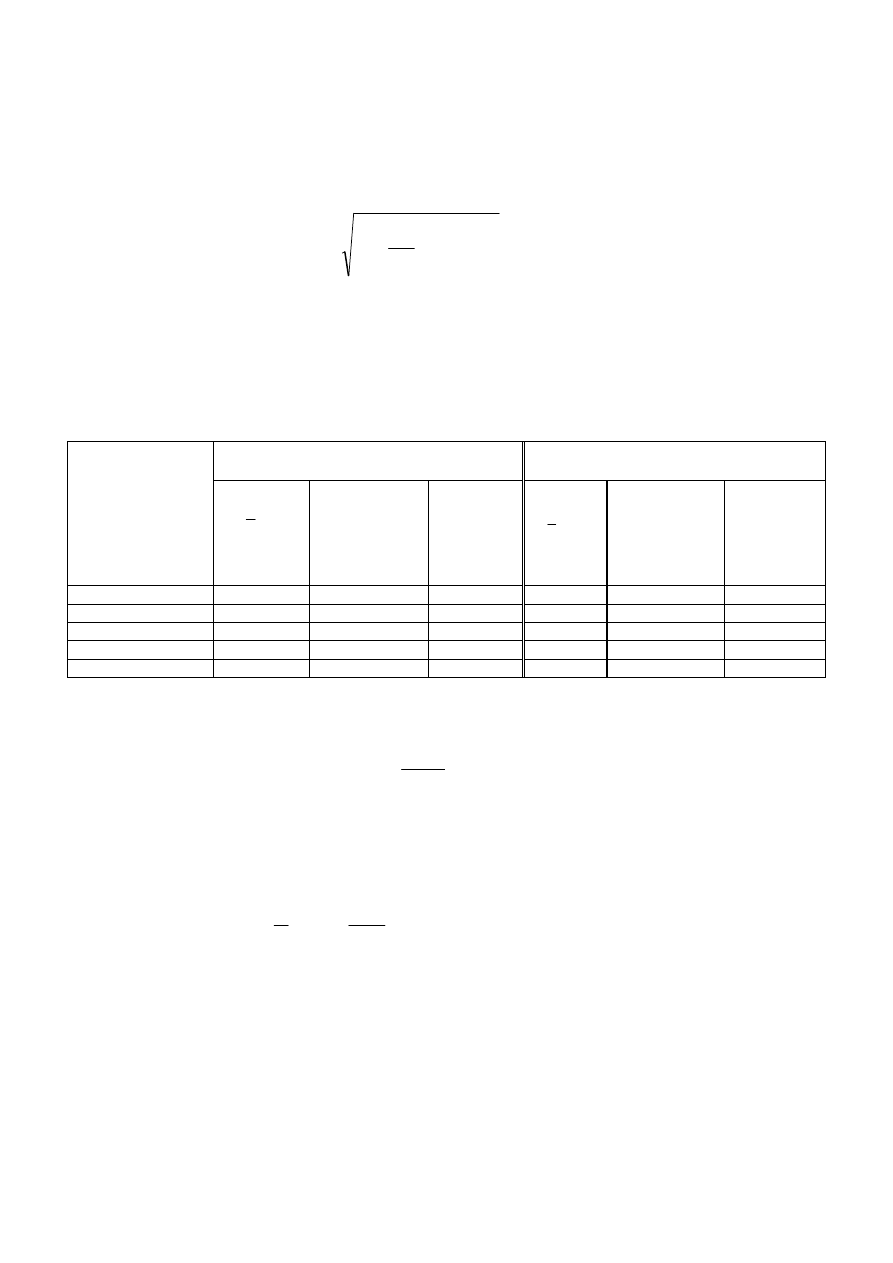
gdzie: X
max
- maksymalny sygnał wejściowy przetwornika, X
min
- minimalny sygnał wejściowy
przetwornika Y
max
- maksymalny sygnał wyjściowy, Y
max
- minimalny sygnał wyjściowy.
Całkowita niepewność standardowa ciśnienia może być obliczona na podstawie prawa
propagacji
niepewności
w
pomiarach
pośrednich
dla
wielkości
wejściowych
nieskorelowanych:
∑
⋅
∂
∂
=
i
i
i
c
)
x
(
u
x
p
)
p
(
u
2
2
.
(12)
Całkowita niepewność standardowa temperatury może być obliczona na podstawie
wyrażenia (9).
Wyniki pomiarów temperatury, ciśnienia i ich niepewności całkowite dla wszystkich punktów
pomiarowych należy zestawić w tabeli 6.
Tabela 6. Wyniki pomiarów ciśnienia i temperatury wrzenia.
Następnie wykorzystując metodę najmniejszych kwadratów dokonać aproksymacji danych
pomiarowych przy pomocy równania Clausiusa –Clapeyrona:
C
T
R
h
)
p
ln(
i
lg
+
⋅
−
=
∆
,
(13)
gdzie:
lg
h
∆
-utajona entalpia (ciepło) parowania kJ/kg, R
i
- indywidualna stała gazowa
kJ/kgK, C-stała całkowania, T- temperatura, K.
Powyższe równanie można przekształcić do postaci:
( )
b
a
+
⋅
=
τ
τ
π
,
(14)
gdzie:
( )
p
ln
=
π
,
T
1
=
τ
,
i
lg
R
h
a
∆
−
=
, b=C.
Ostatecznie otrzymuje się równanie linii prostej w układzie współrzędnych π,τ.
Wykorzystując metodę najmniejszych kwadratów można obliczyć współczynniki a i b
równania (14):
L.p.
Temperatura
Ciśnienie
Średnia
arytmet.
T
, K
Całkowita
niepewność
standardowa
średniej
u(T), K
(z równania 9)
Całkowita
względna
niepewność
standardowa
średniej, %
Średnia
arytmet.
p
,
bar
Całkowita
niepewność
standardowa
średniej
u(p), bar
(z równania 12)
Całkowita
względna
niepewność
standardowa
średniej, %
I punkt pomiarowy
II punkt pomiarowy
III punkt pomiarowy
IV punkt pomiarowy
IV punkt pomiarowy
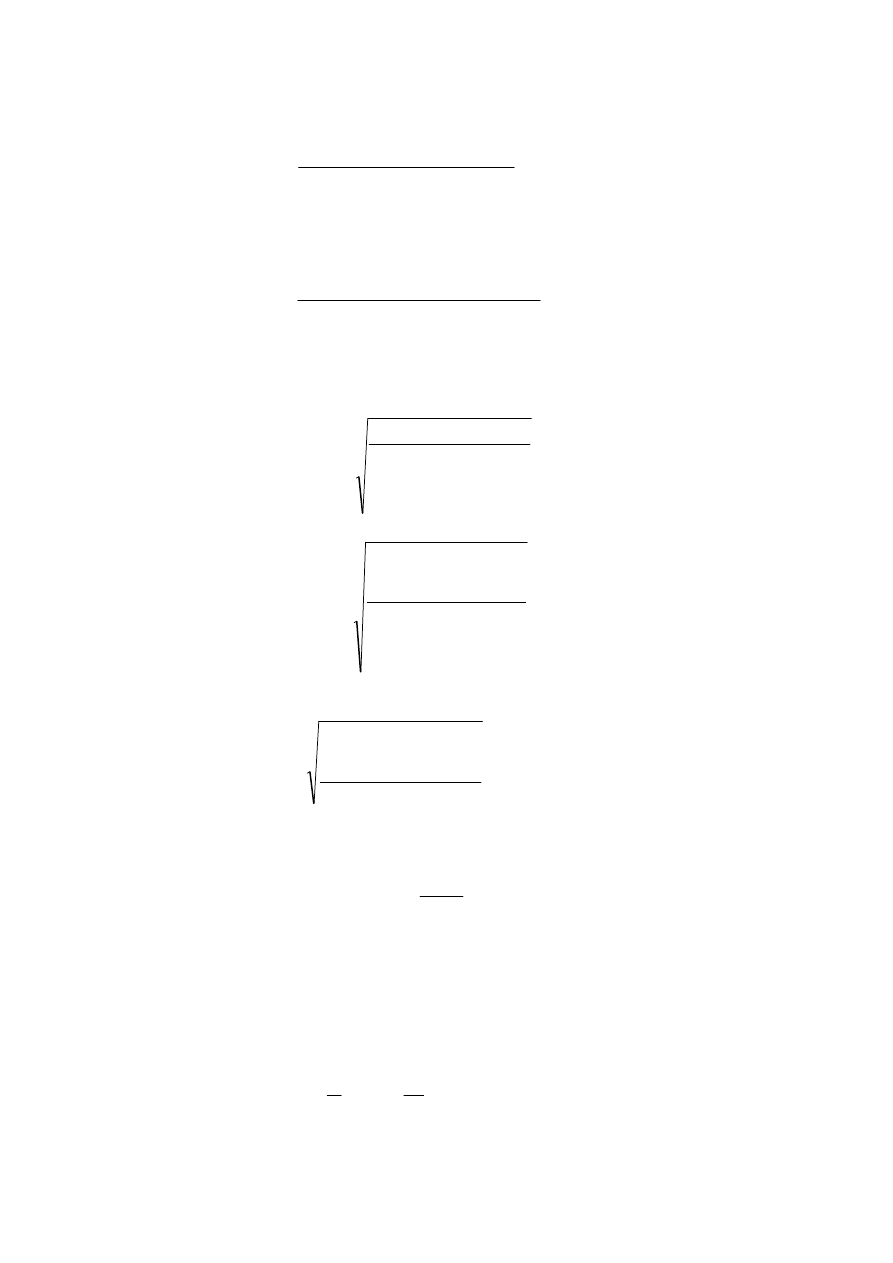
2
1
1
2
1
1
1
−
⋅
⋅
−
⋅
⋅
=
∑
∑
∑
∑
∑
=
=
=
=
=
N
j
j
N
j
j
N
j
j
N
j
j
N
j
j
j
N
N
a
τ
τ
π
τ
π
τ
,
(15)
2
1
1
2
1
1
1
1
2
−
⋅
⋅
⋅
−
⋅
=
∑
∑
∑
∑
∑
∑
=
=
=
=
=
=
N
j
j
N
j
j
N
j
N
j
j
j
N
j
j
j
N
j
j
N
b
τ
τ
π
τ
τ
π
τ
,
(16)
gdzie: N- liczba punktów pomiarowych.
Niepewności standardowe współczynników a i b oblicza się następująco:
2
1
1
2
−
⋅
⋅
=
∑
∑
=
=
N
j
j
N
j
j
y
N
N
s
)
a
(
u
τ
τ
,
(17)
2
1
1
2
1
2
−
⋅
⋅
=
∑
∑
∑
=
=
=
N
j
j
N
j
j
N
j
j
y
N
s
)
b
(
u
τ
τ
τ
,
(18)
(
)
[
]
2
1
2
−
+
⋅
−
=
∑
=
N
b
a
s
N
j
j
j
y
τ
π
.
(19)
Wykorzystując metodę najmniejszych kwadratów dokonać
aproksymacji danych
pomiarowych przy pomocy równania Antoine’a:
( )
T
ln
B
T
R
A
C
)
p
ln(
i
⋅
+
⋅
−
=
,
(20)
gdzie: A, B- stałe w równaniu entalpii parowania w funkcji temperatury (do wyprowadzenia
równania
Antoine’a
przyjęto,
że
entalpia
parowania
jest
liniową
funkcją
temperatury:
T
B
A
h
lg
⋅
+
=
∆
), R
i
- indywidualna stała gazowa kJ/kgK, C-stała całkowania,
T- temperatura, K.
Powyższe równanie można przekształcić do postaci:
( )
( )
γ
τ
β
τ
α
τ
π
+
⋅
+
⋅
=
−1
ln
,
(21)
gdzie:
( )
p
ln
=
π
,
T
1
=
τ
,
i
R
A
−
=
α
, β=B, γ=C.
Przedstawić wyniki pomiarów wraz z ich niepewnościami całkowitymi dla wszystkich
punktów pomiarowych na wykresie w układzie ln(p), T
-1
.
Aby wyznaczyć stałe α,β,γ występujące w równaniu (21), należy rozwiązać układ równań:
( )
( )
( )
( )
(
)
( )
( )
( )
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
=
=
−
=
=
=
−
=
−
=
−
=
−
=
−
=
=
⋅
+
⋅
⋅
+
⋅
=
⋅
⋅
+
⋅
+
⋅
⋅
=
⋅
⋅
+
⋅
+
⋅
=
N
j
j
N
j
j
j
N
j
j
N
j
j
j
N
j
j
N
j
j
N
j
j
j
N
j
j
j
N
j
j
N
j
j
N
j
j
ln
ln
ln
ln
ln
N
ln
1
1
1
1
2
1
1
1
1
2
1
1
1
1
1
1
1
1
1
τ
γ
τ
τ
β
τ
α
τ
π
τ
γ
τ
β
τ
τ
α
τ
π
γ
τ
β
τ
α
π
.
(22)
Naszkicować na wykresie równanie (14) i (20). Porównać własne wyniki pomiarów z danymi
literaturowymi. Dodatkowo wyznaczyć utajone ciepło parowania wody na podstawie
równania Clausiusa –Clapeyrona oraz Antoine’a
lg
h
∆
(wykorzystać
i
lg
R
h
a
∆
−
=
,
T
B
A
h
lg
⋅
+
=
∆
).
Uwaga: Równania (15,16,17,18,19,22) są słuszne, w przypadku gdy niepewności
pomiaru temperatury są znikomo małe w stosunku do niepewności pomiaru ciśnienia oraz gdy
niepewności ciśnienia są jednakowe.