Wyznaczanie współczynnika tarcia statycznego

Ćw.6

Cel ćwiczenia

Poznanie metody wyznaczania współczynnika tarcia statycznego oraz wykazanie zależności siły tarcia od

rodzaju materiału.

Zakres obowiązującego materiału teoretycznego

Zasady dynamiki. Rozkład sił na równi pochyłej. Współczynniki tarcia statyczny i dynamiczny.

Przyrządy i materiały użyte w doświadczeniu

Równia pochyła z płynnie regulowanym kątem nachylenia, zestaw płyt i klocków wykonanych z różnych

materiałów.

Wprowadzenie

Efekt tarcia zewnętrznego pojawia się przy stycznym przesuwaniu kontaktujących się powierzchni dwu

ciał. Jest to proces rozpraszania energii w wyniku działania siły kontaktowej leżącej w płaszczyźnie powierzchni

styku i skierowanej przeciwnie do kierunku ruchu. Tarcie jest zjawiskiem bardzo złożonym, zależnym zarówno

od makroskopowej jak i mikroskopowej struktury przemieszczających się względem siebie warstw

powierzchniowych, a także od wielu czynników zewnętrznych.

Struktura makroskopowa (geometria obszarów rzeczywistego styku, chropowatości i mikronierówności)

decyduje o występowaniu tzw. składowej mechanicznej oporów tarcia. Związana jest ona z odkształcaniem

powierzchni trących i ze wzajemnym wnikaniem kontaktujących się materiałów w mikroszczeliny powierzchni.

Wygładzanie powierzchni początkowo powoduje zmniejszenie siły tarcia, jednak po przekroczeniu pewnego

stopnia gładkości siła tarcia ponownie wzrasta. Wynika to ze zwiększenia się składowej adhezyjnej oporów

tarcia wraz ze wzrostem obszarów rzeczywistego styku. Jest to związane z oddziaływaniami

międzycząsteczkowymi pomiędzy stykającymi się powierzchniami. Niejednorodność powierzchni sprawia, że

pomiary siły tarcia są słabo powtarzalne i dlatego dla wyznaczenia siły tarcia dla danej pary trących się

powierzchni konieczne jest wielokrotne powtórzenie pomiarów i uśrednienie uzyskanych wyników.

Zjawisko adhezji zależne jest od mikroskopowej struktury warstw powierzchniowych, w szczególności od

budowy chemicznej i struktury krystalicznej. Oddziaływania adhezyjne mogą być wynikiem działania sil Van der

Waalsa (im większa polarność powierzchni, tym większa adhezja); sił elektrostatycznych (jeśli występuje

zjawisko elektryzowania się warstw powierzchniowych); a także dyfuzji (szczególnie w przypadku

kontaktujących się polimerów możliwe jest wzajemne dyfuzyjne wnikanie łańcuchów makrocząsteczek).

Jak silny wpływ na tarcie ma struktura chemiczna widać na przykładzie policzterofluoroetylenu (PTFE)

zwanego popularnie teflonem. Współczynnik tarcia PTFE jest mniejszy nie tylko od współczynników tarcia

innych polimerów, np. polietylenu, polistyrenu czy polimetakrylanu metylu, ale jest niższy nawet od

współczynników tarcia szkła. Współczynnik tarcia PTFE jest zbliżony do współczynnika tarcia lodu.

1

Do

najważniejszych czynników zewnętrznych wpływających na opory tarcia należą: temperatura

otoczenia, wielkość i czas działania siły nacisku oraz prędkość poślizgu. W wykonywanym ćwiczeniu można

przyjąć, że wymienione czynniki zewnętrzne nie mają wpływu na pomiary porównawcze różnych par badanych

materiałów, gdyż pomiary wykonywane są w podobnych warunkach przy podobnych i niewielkich siłach

nacisku, w warunkach statycznych.

Podstawy fizyczne metody wyznaczania współczynnika tarcia statycznego

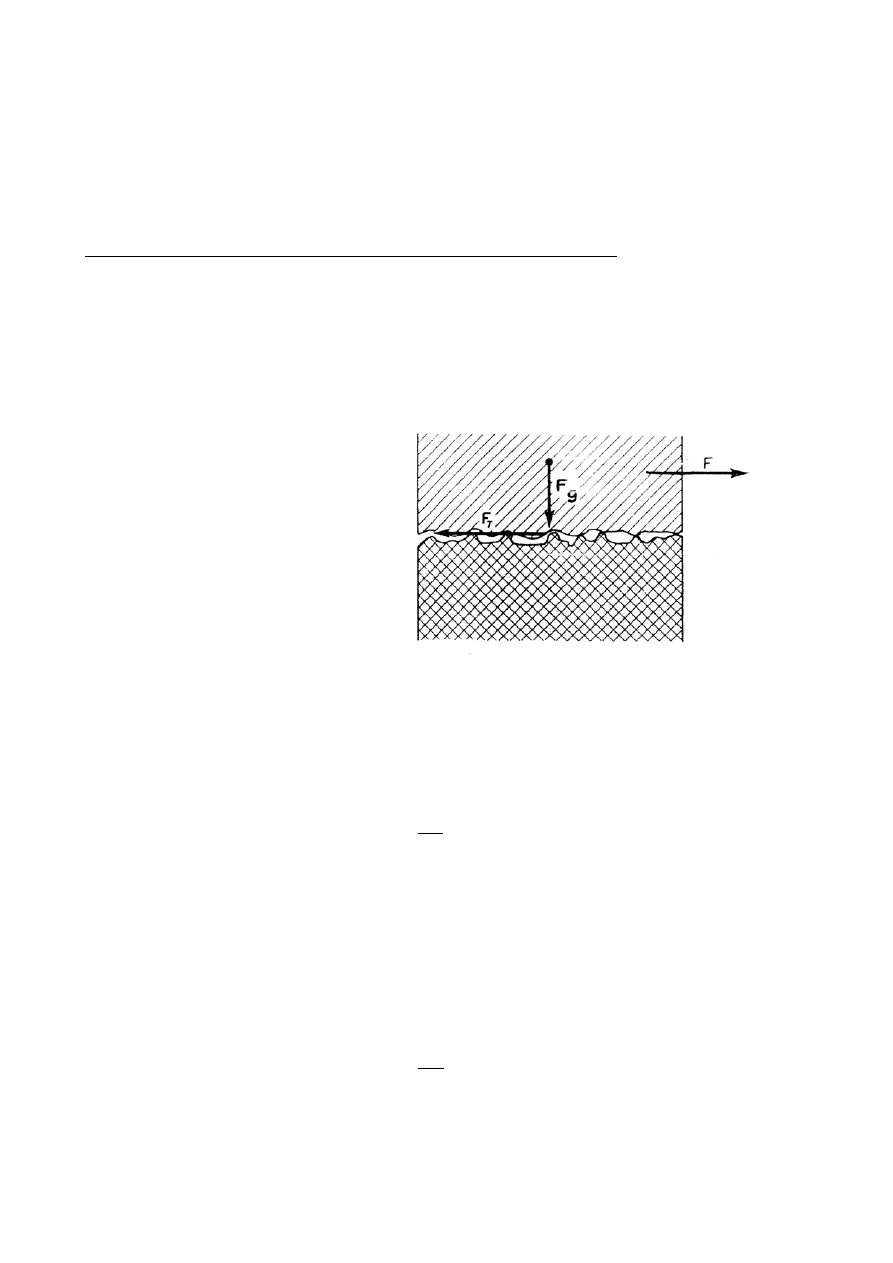
Siły występujące przy przesuwaniu ciała o masie m po poziomej powierzchni przedstawione są na

rysunku 1. Gdy przyłożona siła F jest mniejsza od krytycznej siły tarcia statycznego, ciało spoczywa

nieruchomo. Ze wzrostem siły F siła tarcia statycznego wzrasta do wartości maksymalnej F

TS

, przy której ciało

m zacznie się poruszać.

Rys.1 Siły działające na klocek

przesuwany po powierzchni

poziomej pod wpływem siły

zewnętrznej

F

przy

występowaniu siły tarcia F

T

.

F

TS

jest maksymalną wartością siły tarcia statycznego, która określa współczynnik tarcia statycznego

µ

S

(przy założeniu niezależności

µ

S

od siły nacisku) zgodnie z zależnością:

N

s

TS

F

F

µ

=

(1)

czyli:

N

TS

s

F

F

=

µ

(2)

gdzie F

N

jest siłą nacisku (równą w tym przypadku co do wartości sile ciężkości działającej na klocek: F

g

=mg).

Gdy F przekroczy wartość F

TS

, wypadkowa sił działających na ciało jest różna od zera i zaczyna się ono

poruszać. Przeciwdziałać ruchowi będzie wówczas siła tarcia kinetycznego F

TK

:

N

K

TK

F

F

µ

=

(3)

gdzie µ

K

jest współczynnikiem tarcia kinetycznego zdefiniowanym zależnością:

N

TK

K

F

F

=

µ

(4)

2

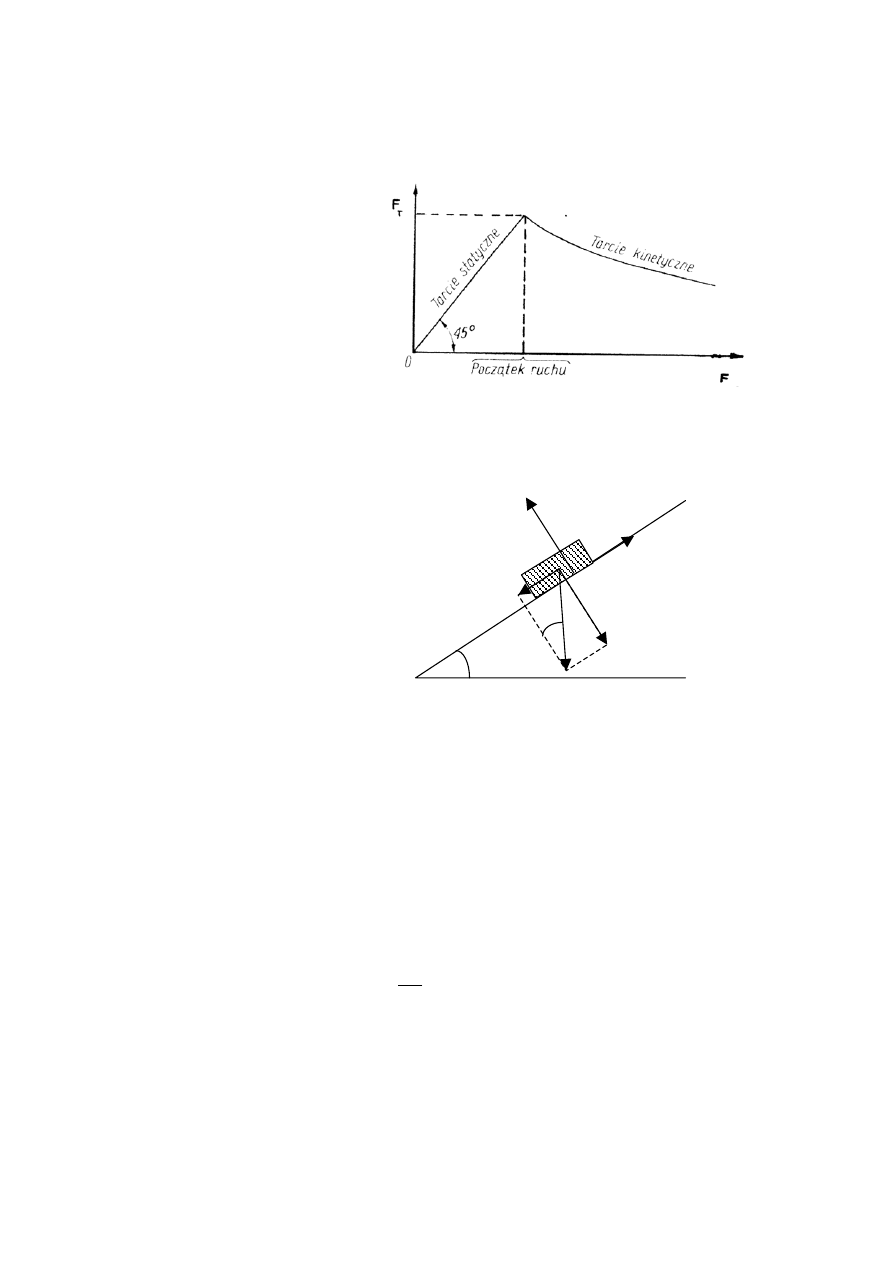
Na ogół siła F

TK

jest mniejsza od F

TS

(µ

K

<µ

S

), tzn., że do poruszenia ciała potrzebna jest większa siła zewnętrzna

niż do dalszego podtrzymywania ruchu tego ciała. Obrazuje to wykres na rys. 2.

Rys.2 Zależność siły tarcia od

siły zewnętrznej F.

Najprostszą metodą wyznaczania współczynnika tarcia statycznego dla danej pary materiałów jest

wyznaczenie najmniejszego kąta nachylenia płaszczyzny dla którego położony na niej klocek zacznie się

zsuwać. Siły działające na klocek leżący na równi pochyłej przedstawione są na rysunku 3.

Rys.3 Siły działające na klocek

leżący na równi pochyłej przy

występowaniu siły tarcia F

T

.

''

g

F

T

F

N

F

g

F

'

g

F

α

α

Klocek pozostaje w spoczynku gdy suma wektorowa działających sił (czyli siła wypadkowa) jest równa zero:

0

=

+

+

T

N

g

F

F

F

r

r

r

. Kąt

α pomiędzy wektorami F

g

i F

N

jest równy kątowi nachylenia równi pochyłej, co wynika z

twierdzenia o kątach o ramionach wzajemnie prostopadłych.

Gdy klocek zaczyna się zsuwać siła tarcia F

T

osiąga wartość maksymalną równą F

TS

. W tym przypadku

prawdziwe są następujące zależności:

α

=

=

α

=

=

cos

sin

''

'

mg

F

F

mg

F

F

g

N

g

TS

a równanie (2) można zapisać w postaci:

α

=

=

µ

tg

F

F

N

TS

s

(5)

gdzie

α jest najmniejszym kątem nachylenia równi przy którym klocek zacznie się zsuwać.

3

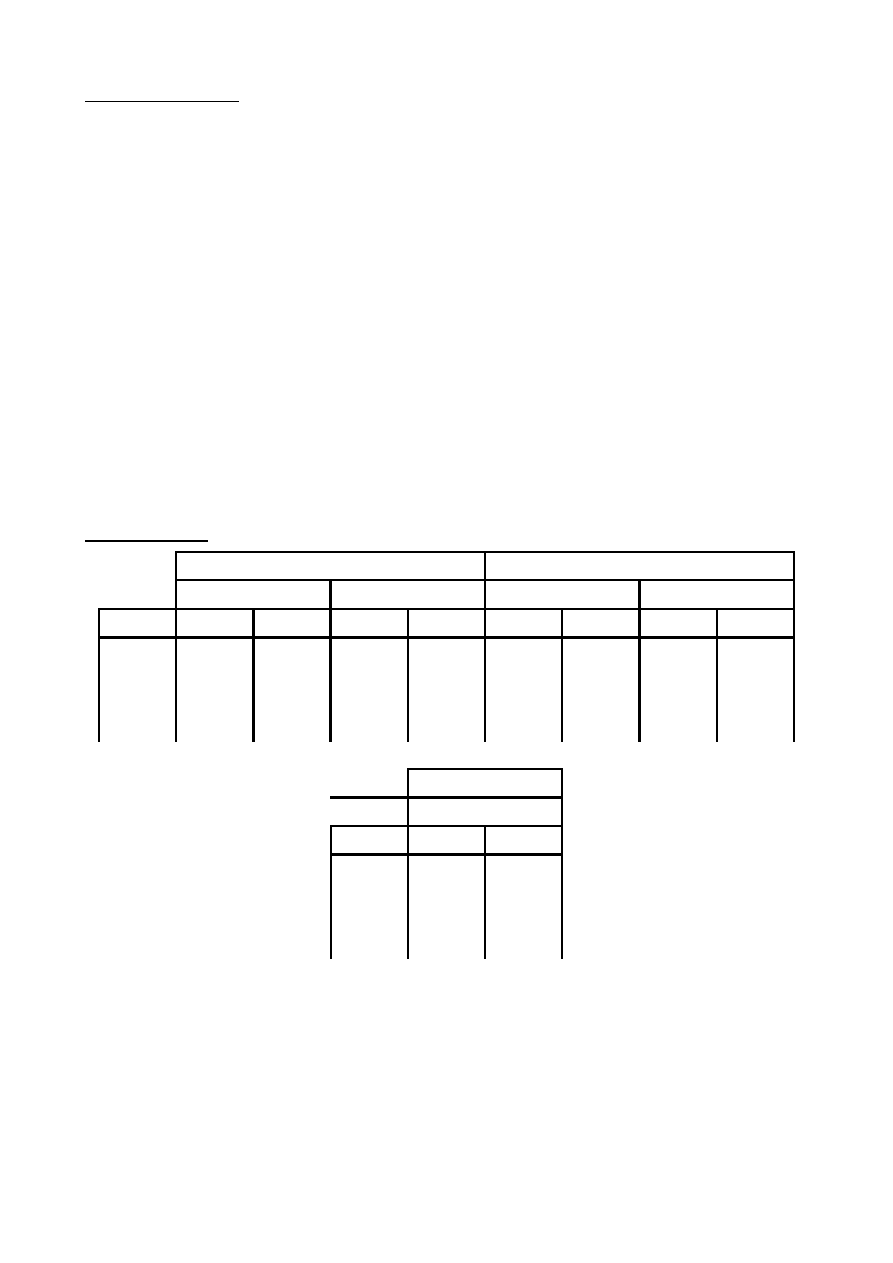
Wykonanie pomiarów

Przetrzeć szmatką powierzchnie płytek i klocków wykonanych z badanych materiałów i sprawdzić stan ich

powierzchni.

UWAGA: Należy bardzo ostrożnie obchodzić się z badanymi płytkami i klockami i unikać ich porysowania. Po

pomiarze należy je układać osobno, badaną powierzchnią skierowaną do góry.

Ułożyć na równi pierwszą z badanych płytek (szklana) i położyć na niej dwa klocki, stalowy i mosiężny

jeden obok drugiego tak, aby nie dotykały do siebie i nie wystawały poza krawędzie płytki. Następnie powoli i

płynnie kręcić pokrętłem podnośnika podnosząc równię do momentu w którym pierwszy klocek poruszy się.

Odczytać na pionowej skali wartość y i na poziomej wartość x i zanotować w kolumnach tabeli pomiarów wg

podanego poniżej wzoru. Podnosić dalej równię aż do momentu poruszenia się drugiego klocka i ponownie

odczytać wartości y i x i zanotować w tabeli. Powtórzyć pomiar N=30 razy. Analogicznie wykonać serie

pomiarów dla drugiej płytki, teflonowej (PTFE) używając tych samych klocków.

Zmienić podłoże na gumowe. Sprawdzić czy powierzchnia gumy nie jest zabrudzona (jeśli jest, to

należy ją oczyścić). Wykonać N=50 pomiarów współczynnika tarcia dla klocka mosiężnego.

Tabele pomiarów

Podłoże szklane

Podłoże teflonowe

Klocek stalowy

Klocek mosiężny

Klocek stalowy

Klocek mosiężny

Nr X y x y x y x y

1

2

.

.

.

30

Podłoże gumowe

Klocek

mosiężny

Nr x y

1
2

.
.
.

50

Tabele pomiarów powinny być przygotowane przed przystąpieniem do wykonywania ćwiczenia i muszą być

załączone do sprawozdania.

4

Opracowanie wyników

1. Po zakończeniu pomiarów wyliczyć wartości tg

α = y/x (czyli współczynniki tarcia statycznego µ

s

) i

uszeregować je od najmniejszej do największej. Uszeregowane wyniki umieścić w tabeli wg poniższego wzoru.

Wartości współczynnika tarcia statycznego (tg

α) uszeregowane od najmniejszej do największej.

Podłoże szklane

Podłoże teflonowe

Podłoże gumowe

Nr Klocek

stalowy

Klocek

mosiężny

Klocek

stalowy

Klocek

mosiężny

Klocek mosiężny

1

2

.

.

30

.

.

50

UWAGA: wszystkie dalsze obliczenia i wykresy należy wykonać bez użycia komputera!!!

2. Dla każdej pary podłoże/klocek sporządzić szereg rozdzielczy wartości

µ

S

i na jego podstawie narysować

histogram zgodnie z regułami podanymi w instrukcji nr 17 (histogramy narysować na papierze milimetrowym).

3. Dla każdego szeregu rozdzielczego obliczyć wartości średnie współczynnika tarcia <

µ

S

> i odchylenia

standardowe S wg wzorów:

N

tg

n

tg

n

tg

n

tg

k

k

S

0

0

2

2

0

1

1

α

+

+

α

+

α

=

α

=

µ

...

(

)

∑

=

α

−

α

=

k

1

i

i

2

0

1

n

tg

tg

N

1

S

gdzie:

tg

α

i

0

- środek i-tej klasy;

n

i

- liczebność i-tej klasy;

k - liczba klas;

N - całkowita liczba pomiarów.

4. Zaznaczyć na histogramach wartości średnie <

µ

S

> i odchylenia standardowe S. Dla największej próby

sprawdzić hipotezę o rozkładzie normalnym za pomocą testu

χ

2

wg instrukcji nr 17.

5. Uszeregować pary podłoże/klocek od najmniejszego do największego współczynnika tarcia.

6. Napisać wnioski.

5