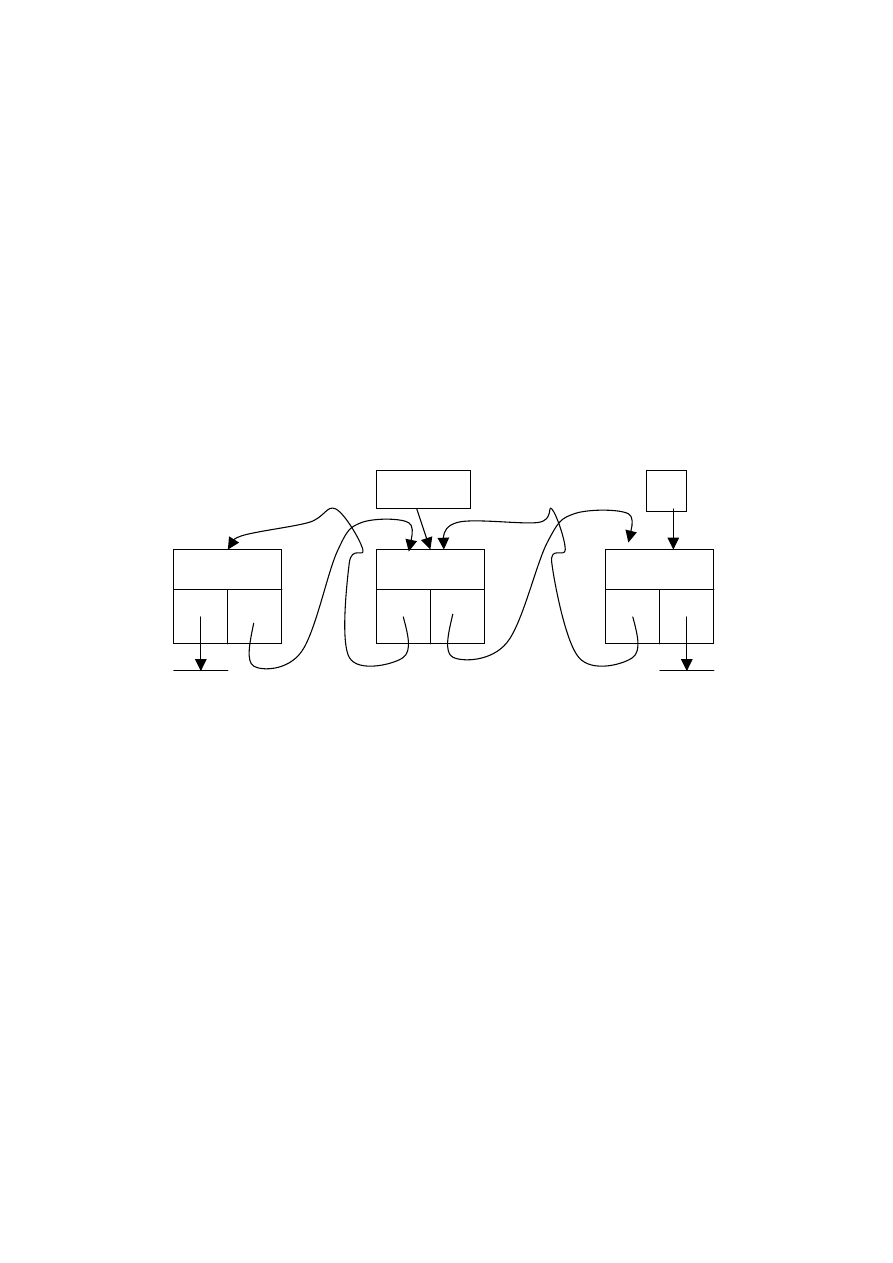
51
10. Lista liniowa dwukierunkowa
Jest to lista złożona z elementów, z których każdy posiada,
oprócz wskaźnika na element następny, również wskaźnik na
element poprzedni.
Zdefiniujmy element listy dwukierunkowej
struct ELEMD
{ int klucz;
ELEMD * left, * right;
};
Rys. 35 Lista liniowa dwukierunkowa
Lista liniowa dwukierunkowa nie ma wyróżnionego
początku ani końca – jest symetryczna. Rolę wskaźnika do
całej listy pełni tutaj wskaźnik name, którego położenie jest w
zasadzie dowolne, może więc być używany, na przykład, do
wyszukiwania elementów.
Z powyższego wynika również, że algorytmy usuwające
elementy powinny sprawdzać, czy usuwany element nie jest
aktualnie wskazywany przez wskaźnik do całej listy. Jeśli tak,
wskaźnik do całej listy należy wcześniej przesunąć na inny
element.
7
2
4
name
p
52
ELEMD *q = new ELEMD;
p →
→
→
→ left →
→
→
→ right = q;
q →
→
→
→ left = p →
→
→
→ left;
p →
→
→
→ left = q;
q →
→
→
→ right = p;
Rys. 36 Przykładowy algorytm wstawiania nowego
elementu, wskazywanego przez q, przed element
wskazywany przez p (założono, że element stojący
na lewo od p istnieje)
p →
→
→
→ left →
→
→
→ right = p →
→
→
→ right;
p →
→
→
→ right →
→
→
→ left = p →
→
→
→ left;
delete p;
Rys. 37 Przykładowy algorytm usuwania elementu
wskazywanego przez p (przy założeniu, że element
usuwany nie jest elementem skrajnie prawym, ani
skrajnie lewym)
Drzewa i lasy
11. Rekurencyjna definicja drzewa
Drzewo, podobnie jak omawiana w rozdziale poprzednim
lista, jest strukturą, którą możemy zdefiniować w sposób
rekurencyjny.
53
Oto ta definicja:
Niech wierzchołek w (element drzewa) będzie pewnego
typu T, wtedy:
1. Jeżeli dowolna, skończona, rozłączna i nie należąca do
drzewa liczba wierzchołków typu T, do niego
dowiązanych jest drzewami, to w jest drzewem.
2. Zbiór pusty wierzchołków jest drzewem.
Jest to typowa definicja rekurencyjna, w której punkt 2
stanowi warunek stopu definicji.
Pojęcie wierzchołek (węzeł) i dowiązanie (łuk) zostały
zapożyczone z teorii grafów. Poniższy rysunek objaśnia
podaną definicję.
a) b)
. . .
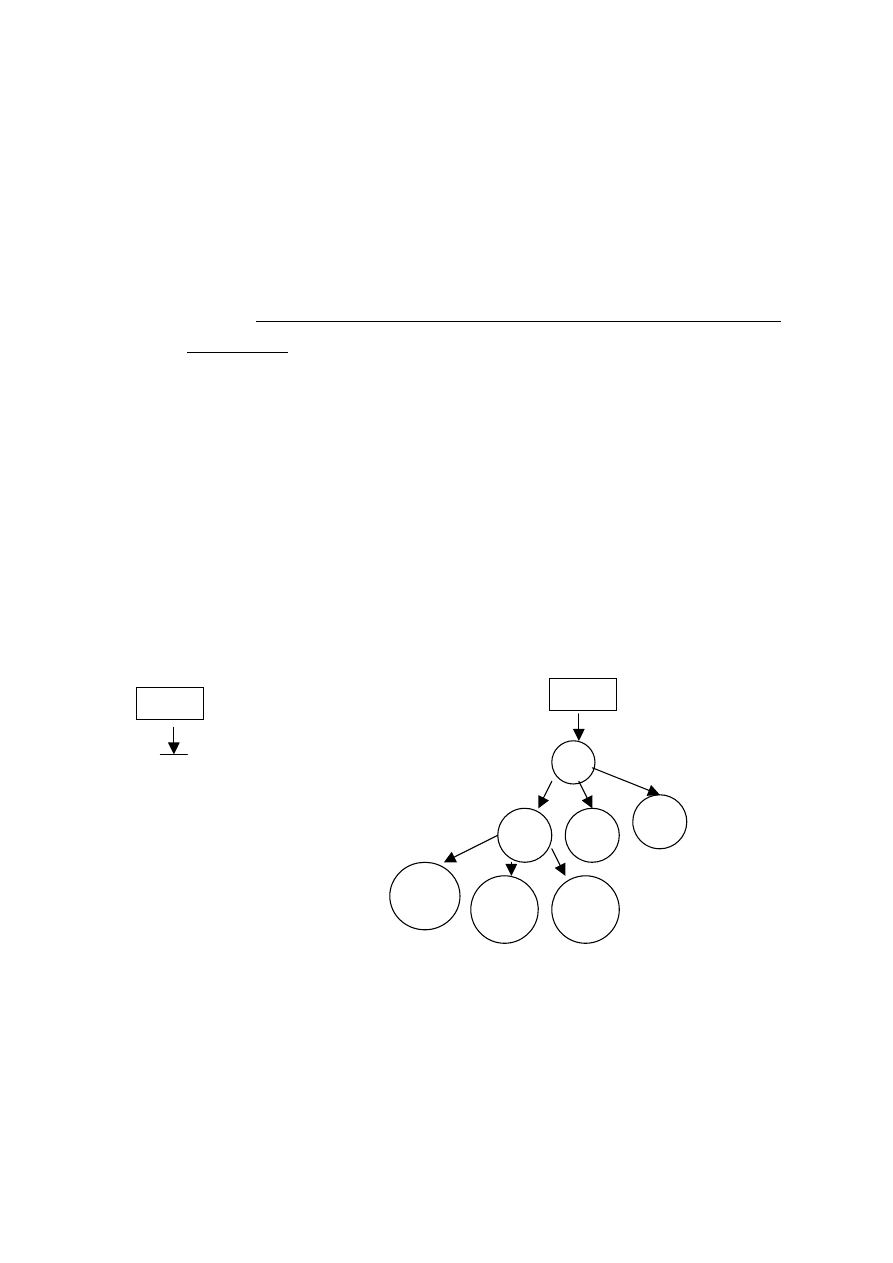
Rys. 38 Rekurencyjna definicja drzewa: a) drzewo puste,
b) drzewo niepuste.
root
root
w
w
1
w
2
w
n
w
11
w
12
w
13
54
Definicje podstawowych pojęć
1. Wierzchołki, które są bezpośrednio dowiązane do
danego wierzchołka, nazywamy jego bezpośrednimi
potomkami, albo bezpośrednimi następnikami (synami
węzła).
2. Z kolei – wierzchołek taki nazywać będziemy
bezpośrednim poprzednikiem (ojcem) tych węzłów.
3. Synów tego samego ojca nazywamy braćmi.
4. Wierzchołek, który nie ma bezpośredniego poprzednika
nazywamy korzeniem drzewa. Korzeniem drzewa
nazywa się też wskazanie do tego elementu. Jest to
jednocześnie wskazanie do całego drzewa.
5. Wierzchołki,
które
nie
mają
bezpośrednich
następników,
nazywamy
liśćmi
drzewa.
6. Elementy nie będące liśćmi nazywamy węzłami
wewnętrznymi drzewa.
7. Drzewem uporządkowanym nazywamy drzewo, w
którym dla każdego węzła wewnętrznego na jego
synach określona jest ta sama relacja liniowego
porządku.
8. Jeżeli dany węzeł ma poziom i, to wszystkie jego
bezpośrednie następniki mają poziom i+1. Założymy,
że korzeń drzewa ma poziom 1.
55
9. Maksymalny poziom wierzchołków drzewa nazywamy
wysokością, albo głębokością drzewa.
10. Stopniem drzewa nazywamy maksymalną liczbę
wierzchołków, jakie można dowiązać do każdego z
węzłów.
11. Ścieżką w drzewie jest ciąg jego wierzchołków
a
1
, a
2
, . . . ,a
n
taki, że dla każdego i = 2, 3, . . . , n para
(a
i-1
, a
i
) jest krawędzią, łączącą dany wierzchołek
wewnętrzny
z
jego
bezpośrednim
potomkiem.
Wierzchołki
wewnętrzne
to
zbiór
wszystkich
wierzchołków
drzewa
za
wyjątkiem
liści.
12. Liczba krawędzi, jaką trzeba przejść od korzenia do
poziomu danego wierzchołka w nazywamy długością
drogi wierzchołka
w. Długość drogi korzenia
wynosi 1. Ogólnie - długość drogi wierzchołka na
poziomie i wynosi i.
13. Lasem nazywać będziemy uporządkowany zbiór
drzew. Uporządkowanie drzew w lesie polega na
uporządkowaniu korzeni kolejnych drzew. Spina się je
w las poprzez umieszczenie wskaźników do ich korzeni
w tablicy, lub w liście wskaźników.
Lista liniowa jednokierunkowa jest szczególnym przypadkiem
drzewa. Jest to drzewo stopnia pierwszego.
12. Drzewo binarne
W praktyce używa się zwykle drzew niewysokiego stopnia,
na przykład drugiego (mówimy wtedy o drzewie binarnym).
56
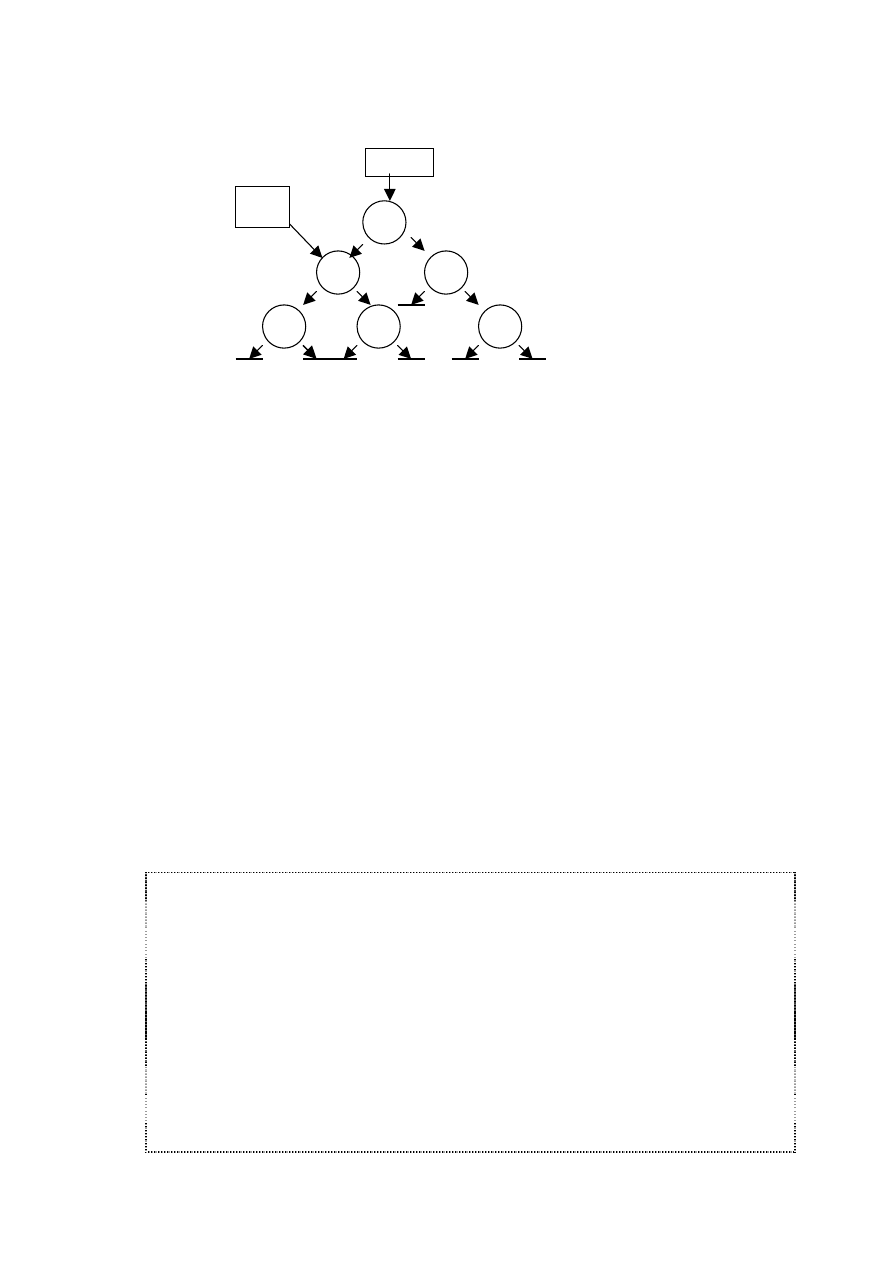
Rys. 39 Przykład drzewa binarnego ( ptr - wskazanie
dowolnego węzła drzewa)
Algorytm tak zwanego naturalnego przekształcenia
dowolnego lasu w drzewo binarne
Jest
to
algorytm,
który umożliwia przekształcenie
dowolnego lasu, złożonego z dowolnej ilości drzew o różnych
stopniach, w pojedyncze drzewo binarne. Jest zupełnie
naturalnym, że algorytmy obsługi drzew o ustalonym,
niewysokim stopniu, będą prostsze i bardziej efektywne niż
algorytmy dotyczące drzew charakteryzujących się dość dużą
dowolnością.
Algorytm
tak
zwanego
naturalnego
przekształcenia
dowolnego lasu w drzewo binarne skonstruować można wg.
poniższych kroków:
1. Przyjmij za korzeń drzewa binarnego korzeń pierwszego
drzewa w lesie.
2. Przenoś kolejne węzły drzew lasu do drzewa binarnego w ten
sposób, aby:
2.1. ich pola left wskazywały listę wiązaną synów tego węzła
w drzewie oryginalnym,
2.2. lista ta była wiązana poprzez pola right każdego z
przenoszonych węzłów,
2.3. zasada ta dotyczy również wiązania korzeni
poszczególnych drzew lasu.
root
7
8
2
5
1
4
ptr
57
las 0 1 2 ... N-1
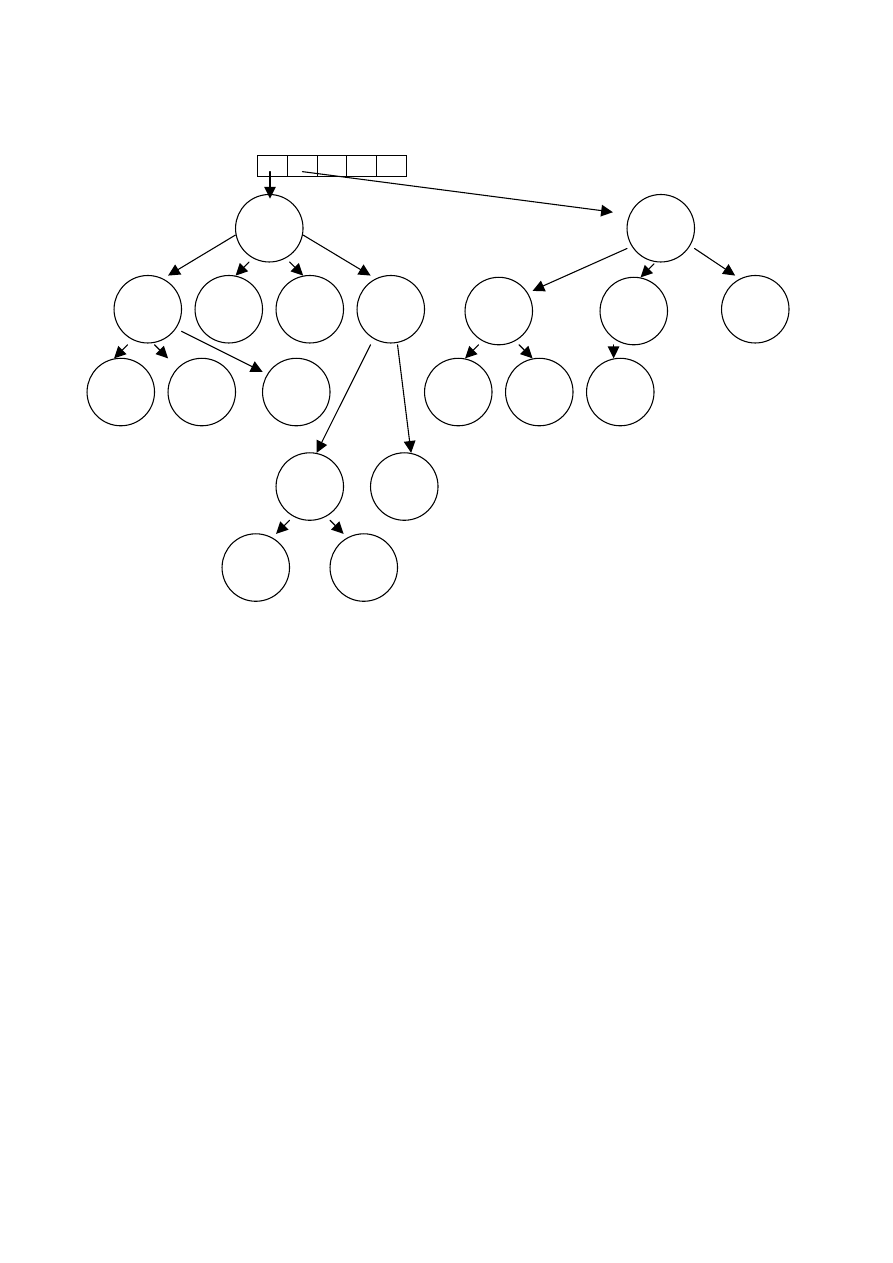
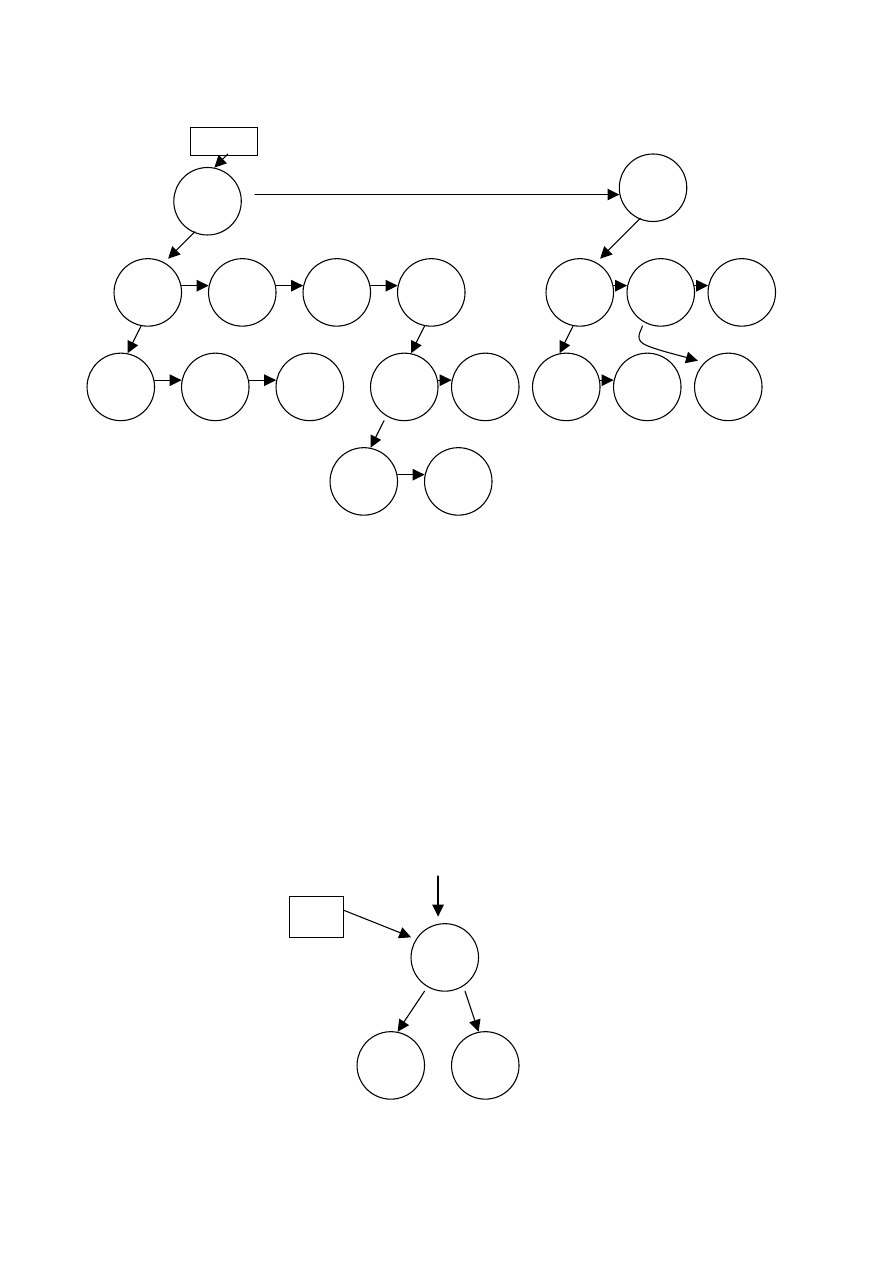
Rys. 40 Las złożony z dwóch drzew. N-elementowa tablica
wskaźników las przechowuje wskazania do
kolejnych drzew w lesie
Rys. 40 przedstawia przykładowy las złożony z dwóch
drzew o różnym stopniu, rys. 41 – drzewo binarne otrzymane
z przekształcenia tego lasu za pomocą wyżej omawianego
algorytmu.
Po przekształceniu lasu w drzewo binarne i wykonaniu na
nim wszystkich niezbędnych operacji, takich jak: wyszukanie
węzła, modyfikacja jego zawartości, bądź nawet usunięcie lub
wstawienie nowego węzła, drzewo binarne można z powrotem
przekształcić do pierwotnej, naturalnej postaci.
1
3
2
7
8
13
19
17
14
4
18
16
15
6
5
12
9
11
10
58
Rys. 41 Drzewo binarne powstałe z przekształcenia lasu
przedstawionego na rys.40
Przeglądanie drzewa binarnego
Niech Q(ptr) będzie operacją, którą trzeba wykonać na
węźle wskazywanym przez ptr, oraz wszystkich węzłach
leżących poniżej węzła wskazywanego przez ptr (patrz
rys. 39). Jeśli ptr = root, czyli wywołamy procedurę Q dla
wskazania korzenia drzewa, wtedy procedura ta wykonana
zostanie dla całego drzewa.
Rys. 42 Węzły drzewa binarnego
root
7
8
12
14
3
1
2
19
17
6
5
4
12
9
11
10
18
16
15
C
B
A
ptr
59
Rekurencyjną metodę zapewniającą przejrzenie całego
drzewa o dowolnym kształcie i rozmiarach począwszy od
węzła wskazywanego przez ptr (węzeł A na rys. 42)
sformułować można następująco:
Wykonaj żądaną operację na węźle, w którym się znajdujesz
a następnie zgodnie z przyjętą zasadą odwiedź lewy
wierzchołek dowiązany, następnie zgodnie z przyjętą zasadą
odwiedź prawy wierzchołek dowiązany.
W tym opisie metody najważniejszym jest sformułowanie
„zgodnie z przyjętą zasadą”. Tutaj bowiem ukryte jest
rekurencyjne wywołanie metody. Uzyskany efekt najlepiej
obrazuje poniższy rysunek.
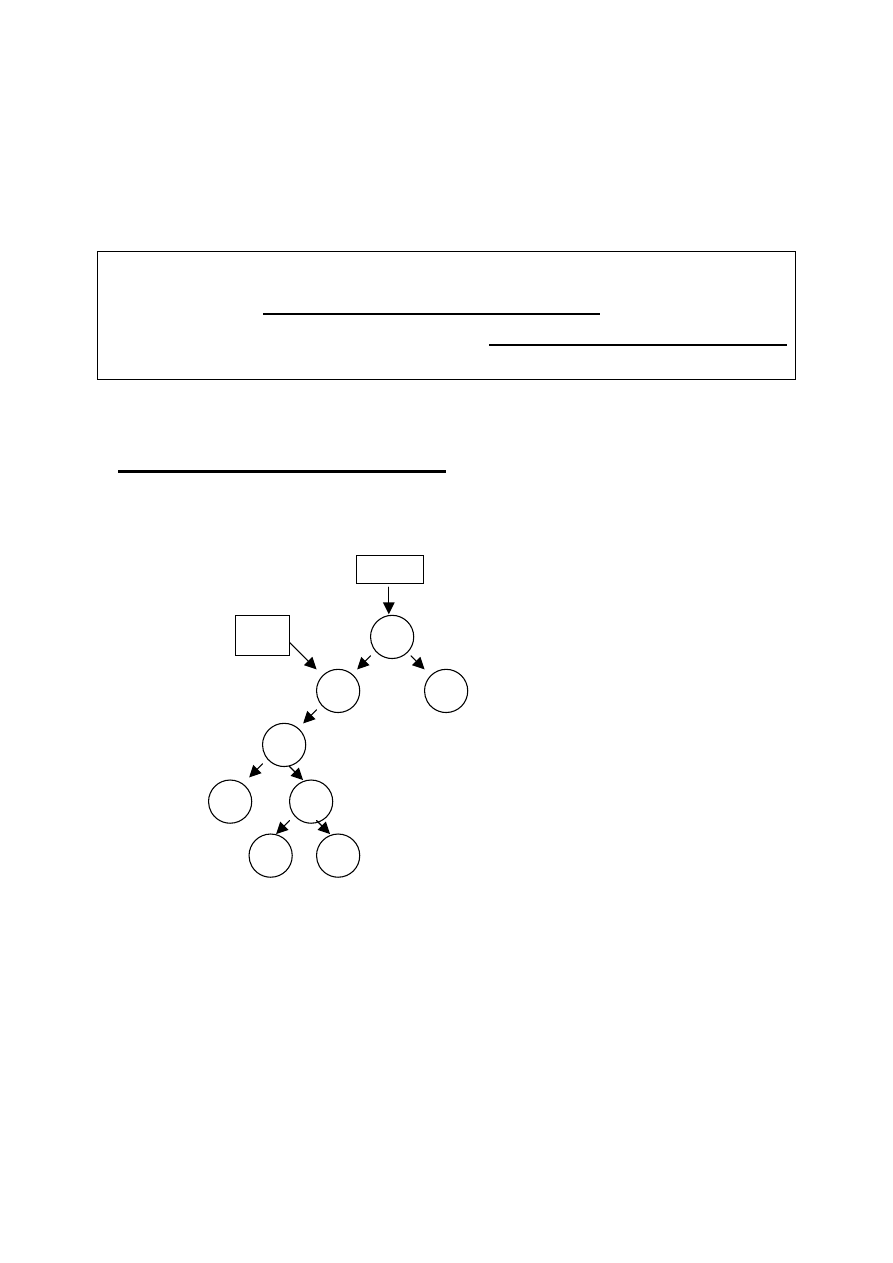
Rys. 43 Kolejność wykonywania operacji Q(ptr) na
węzłach drzewa binarnego przy użyciu metody
preorder.
Mamy tu do czynienia ze schematem odwiedzania węzłów
drzewa binarnego, który nazwany został metodą zstępującą,
albo metoda porządku poprzedzającego (z ang. preorder ).
root
1
3
4
5
8
2
ptr
7
6
60
Jest to schemat A – B – C. A oznacza wykonanie operacji
na węźle, B lub C - jedynie jego odwiedzenie.
Dwa dalsze możliwe schematy to:
• B – A – C inorder - metoda wstępująca lub
porządek następujący,
• B – C – A postorder - metoda symetryczna lub
porządek wewnętrzny.
Rekurencyjna funkcja zapewniająca, przy zastosowaniu
metody preorder, wykonanie procedury Q(ptr) dla całego
poddrzewa wskazywanego przez ptr będzie miała w notacji
języka C/C++ postać:
void preorder ( BIN *ptr)
{
if (ptr)
{
Q(ptr);
preorder(ptr → left); preorder(ptr → right);
}
}
13. Drzewa binarnych poszukiwań
Niech poniższy ciąg nie powtarzających się liczb
całkowitych będzie ciągiem kluczy, które chcemy wstawić do
drzewa binarnego w sposób uporządkowany.
7 3 6 9 1 8 5
61
Poszukując liścia, którego następnikiem ma być kolejny
wstawiany wierzchołek, zastosujmy następującą rekurencyjną
metodę:
1. jeżeli wartość wstawiana jest mniejsza od wartości klucza
badanego węzła, należy poprzez pole left przejść do
lewego węzła,
2. jeżeli wartość wstawiana jest większa od wartości klucza
badanego węzła, należy poprzez pole right przejść do
prawego węzła,
3. powyższe można zakończyć po napotkaniu węzła,
którego lewe, lub prawe wskazanie jest wskazaniem
pustym, wskazania tego należy użyć w celu wstawienia
węzła.
Zauważmy, że poszukując miejsca wstawienia nowego
węzła poruszamy się wzdłuż jednej tylko ścieżki w drzewie i
że miejsce wstawienia jest tylko jedno.
Wyżej opisana metoda wstawiania węzłów do drzewa
binarnego, chociaż ma w istocie charakter rekurencyjny (pk. 3
metody stanowi warunek stopu), to ze względu na to, że
poruszamy się wzdłuż jednej tylko ścieżki, może być łatwo
zrealizowana za pomocą algorytmu iteracyjnego.
Otrzymane w ten sposób drzewa binarne, ze względu na swe
szczególne, opisane niżej, własności nazywamy drzewami
binarnych poszukiwań (DBP).
62
Rys. 44 Drzewo binarnych poszukiwań wygenerowane po
otrzymaniu ciągu kluczy 7 3 6 9 1 8 5
Generowanie drzew binarnych poszukiwań stanowi jedną z
najdoskonalszych metod sortowania informacji. Aby bowiem
znaleźć w drzewie wierzchołek o określonej wartości klucza,
lub stwierdzić, że klucz o takiej wartości nie występuje w
drzewie, wystarczy poruszać się wzdłuż jednej tylko ścieżki.
Oto pełna definicja drzewa binarnych poszukiwań:
Drzewem binarnych poszukiwań nazywać
będziemy drzewo binarne, w którym dla
każdego węzła wewnętrznego, klucz jego
lewego następnika jest mniejszy, a klucz
prawego następnika – większy, od klucza
tego węzła.
Maksymalna liczba porównań, jakie trzeba wykonać, aby
znaleźć jakikolwiek wierzchołek, jest równa wysokości DBP.
Oczywiście im drzewo jest mniej zrównoważone (ma większą
wysokość), tym maksymalna liczba porównań jest większa.
root
7
1
8
5
9
3
ptr
6
63
W idealnym przypadku - drzewa dokładnie wyważonego,
drzewo binarne o wysokości n zawiera aż 2
n
– 1 węzłów.
Korzyści, jakie osiągamy z użycia DBP do sortowania danych,
wzrastają więc nieprawdopodobnie szybko ze wzrostem ilości
tych danych, co jest kolejną pozytywną cechą DBP. Obrazuje
to poniższa tabela
Ilość węzłów w DBP
Maksymalna liczba
porównań
1
3
15
1023
16383
65535
1
2
4
10
14
16
Rys. 45 Zależność między ilością węzłów w DBP a
maksymalną ilością porównań, jakich trzeba
dokonać, aby znaleźć wierzchołek o żądanym
kluczu w dokładnie wyważonym DBP.
Algorytm usuwania węzłów różnych od korzenia w DBP
rozbić można na trzy przypadki:
• jeśli węzeł usuwany jest liściem, wystarczy zwolnić
pamięć dla tego węzła a jego wskazaniu przypisać
wskazanie puste,
• jeśli węzeł usuwany ma jednego potomka, należy
wskazaniu usuwanego węzła przypisać wskazanie tego
potomka,
• natomiast jeśli węzeł usuwany ma dwóch potomków,
należy wskazaniu tego węzła przypisać wskazanie
lewego potomka, a następnie – wypięte w ten sposób
poddrzewo, rozpoczynające się od prawego następnika
64
usuwanego węzła, wpiąć do DBP tak jakby się wpinało
nowy pojedynczy węzeł.
14. Drzewa zrównoważone i idealnie zrównoważone
Jak już zauważyliśmy, korzyści jakie wynosimy, używając
drzew binarnych poszukiwań, są tym mniejsze, im bardziej
uporządkowany jest ciąg kluczy kolejno wstawianych węzłów.
W skrajnym przypadku, to jest uporządkowanego ciągu
kluczy, drzewo binarnych poszukiwań degeneruje się do
uporządkowanej
listy
liniowej,
gdzie
średni
czas
wyszukiwania jest tylko rzędu n/2 (n jest ilością węzłów).
W takich sytuacjach warto konstruować tak zwane drzewa
zrównoważone i drzewa idealnie zrównoważone.
Drzewem zrównoważonym nazywamy drzewo binarne, w
którym dla każdego węzła wysokość jego lewego i prawego
poddrzewa różni się nie więcej niż o jeden. Od nazwisk
odkrywców zostały one również nazwane drzewami AVL.
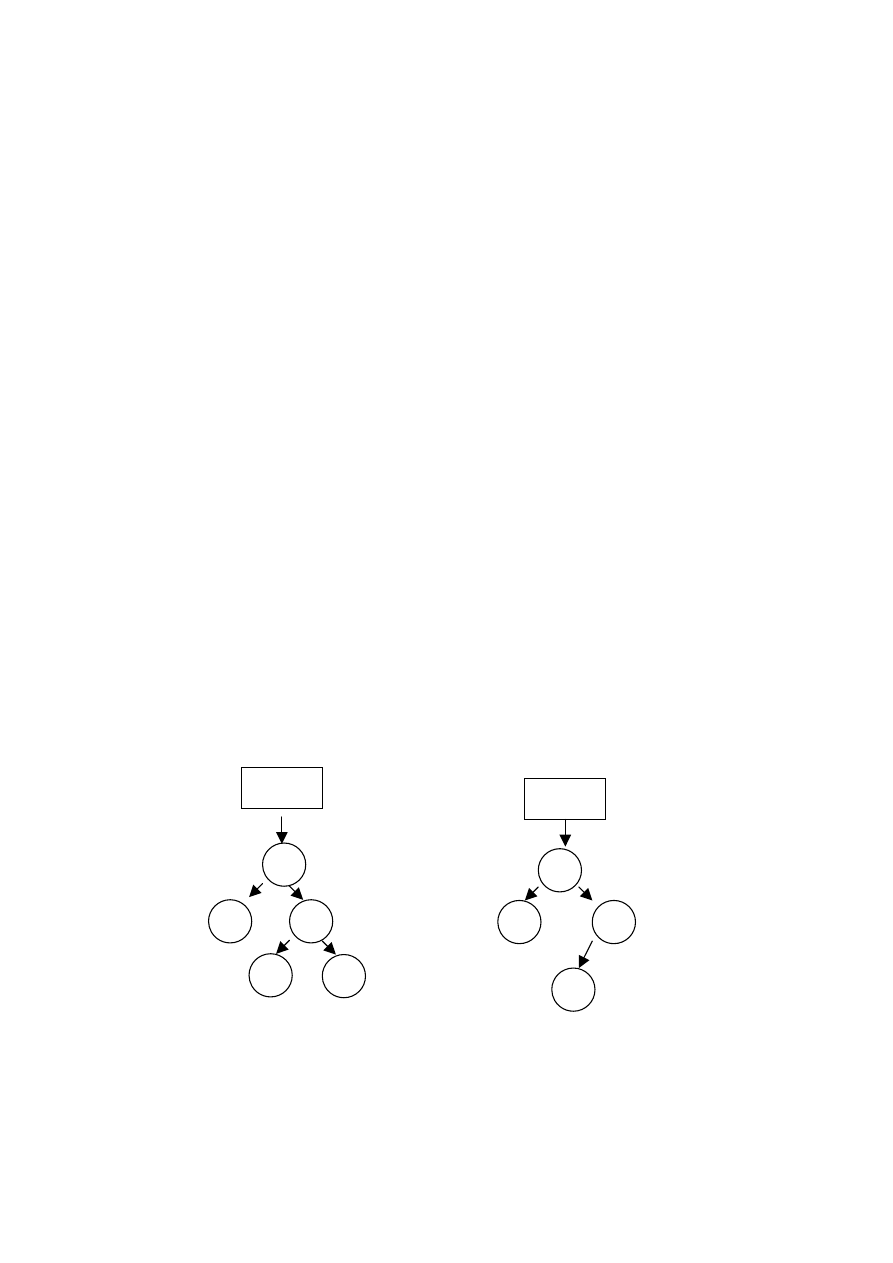
a) b)
Rys. 46 Przykłady drzew: a) drzewo zrównoważone,
b) drzewo idealnie zrównoważone
3
4
5
root
6
3
root
5
4
6
7
65
Z kolei drzewem idealnie zrównoważonym nazywać
będziemy drzewo binarne, w którym wszystkie liście znajdują
się na jednym, lub dwóch poziomach. Oczywiście nie każde
drzewo
zrównoważone
musi
być
drzewem
idealnie
zrównoważonym.
15. Drzewa z priorytetem (HPO-drzewa albo Kopce).
Sterty
W rozdziale poświęconym listom omówiliśmy listy z
priorytetem (HPO-kolejki). Zupełnie podobne zastosowania
mają drzewa z priorytetem, zwane również HPO-drzewami,
lub kopcami.
HPO-drzewa są to drzewa binarne uporządkowane według
priorytetów i zbudowane według zasady:
Dla każdego węzła wewnętrznego
priorytety jego następników są nie
większe od priorytetu tego węzła.
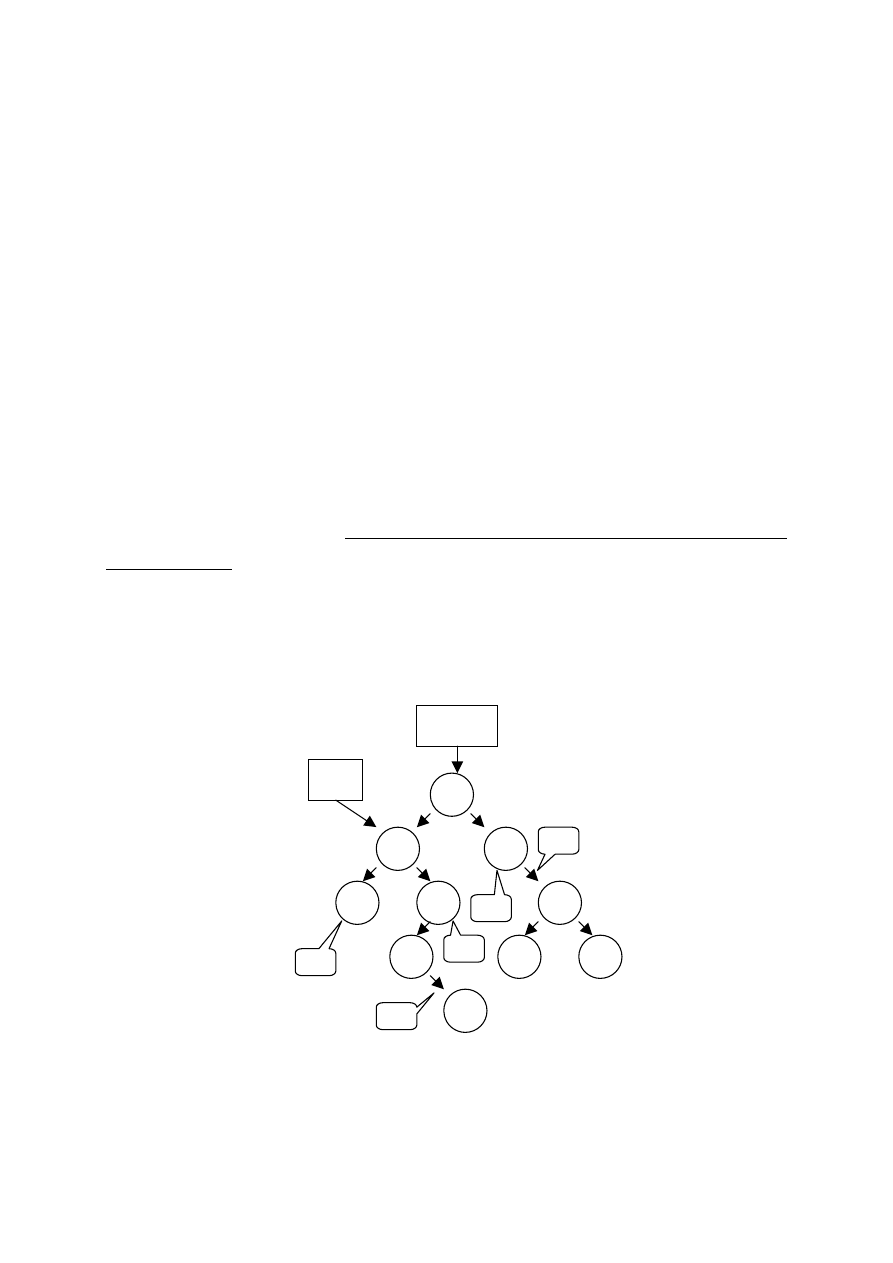
Rys. 47 Przykładowy kopiec. „Dymki” z wartością 11 w
środku wskazują dopuszczalne miejsca wstawienia
węzła o wartości priorytetu równej 11.
20
root
17
15
17
14
10
10
13
3
7
11
11
11
11
11
ptr
66
W HPO-drzewie węzeł o najwyższym priorytecie znajduje
się zawsze w korzeniu. Podobnie jak w HPO-kolejce do węzła
tego istnieje bezpośredni (a więc bardzo szybki) dostęp
poprzez wskazanie do całego drzewa.
Jak już o tym wcześniej mówiono, im z wyższym drzewem
mamy do czynienia, tym dłuższy jest czas wyszukiwania
węzłów. Czas ten jest najkrótszy z możliwych dla drzewa
idealnie zrównoważonego, gdzie złożoność obliczeniowa
algorytmu wyszukiwania wynosi O(log N). Otrzymanie
drzewa idealnie zrównoważonego dla kopca nie jest
oczywiście zawsze możliwe. (Ćwiczenie: dlaczego ?). Można
jedynie zadbać o to, aby algorytmy wstawiające, lub
usuwające
węzły
„dbały”
o
możliwie
największe
zrównoważenie HPO-drzewa.
Natomiast, jeśli zrezygnować z uporządkowania węzłów w
wyżej omawianym drzewie i zażądać, aby drzewo było
idealnie zrównoważone, otrzymamy drzewo binarne o nazwie
sterta.
16. Drzewa decyzyjne
Drzewa decyzyjne najczęściej służą do wyodrębniania
wiedzy z zestawu przykładów (
eksploracja danych
).
Załóżmy, że posiadamy zestaw przykładów, opisanych przy
pomocy kilku atrybutów. Z każdym obiektem zwiążmy jakąś
decyzję (to co otrzymaliśmy nazywamy
tabelą decyzyjną
).
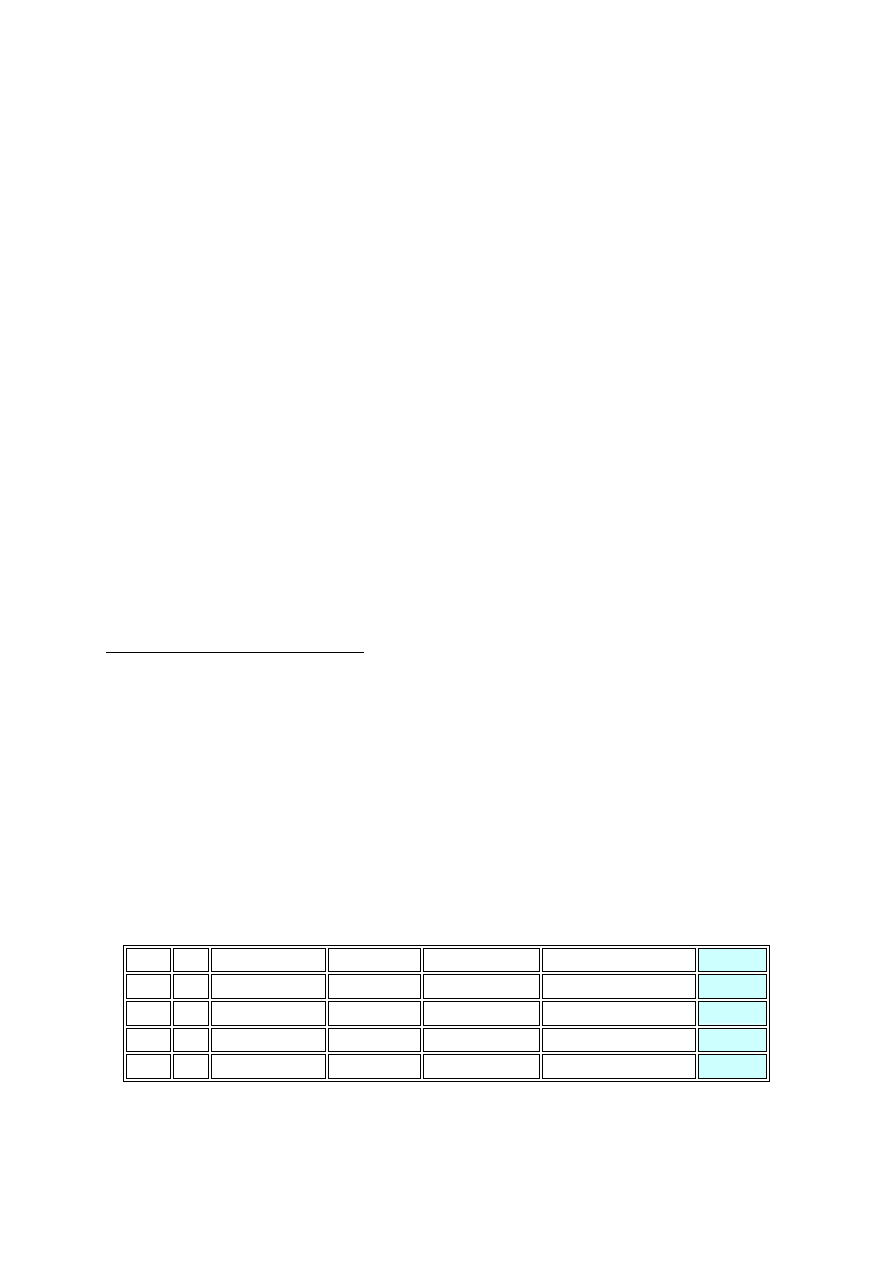
Wiek Płeć Wykształcenie Języki obce Doświadczenie Ogólna prezentacja Przyjęty
25
m
2
4
1
4
nie
22
k
4
3
4
2
nie
21
m
4
5
5
4
tak
29
m
1
3
2
3
nie
Rys. 48. Przykładowa tabela decyzyjna
67
Załóżmy,
że
tabelę
decyzyjną
stworzono
w
celu
zautomatyzowania procesu przyjmowania kandydatów do
pracy w dużej firmie. Rzeczywiste tabele tego typu liczą
nawet setki wierszy.
W naszym przykładzie wprowadzono atrybuty decyzyjne:
Płeć, Wykształcenie, Języki obce, Doświadczenie i Ogólna
prezentacja, oraz - atrybut decyzyjny: Przyjęty. Wartości
atrybutów decyzyjnych (za wyjątkiem płci) są kodowane w
skali od 1 do 5. Atrybut decyzyjny przyjmuje dwie wartości:
tak, nie.
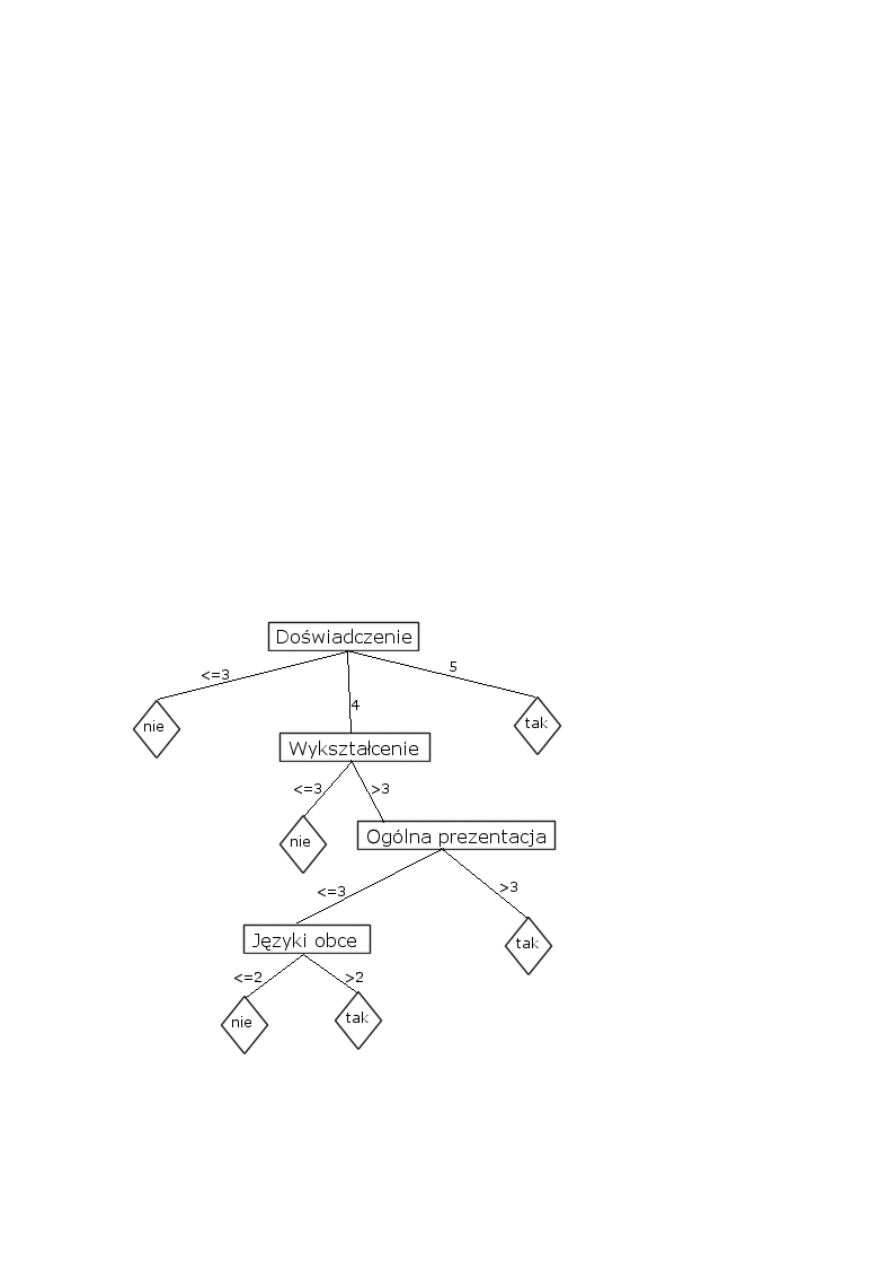
Na podstawie tabeli decyzyjnej tworzymy drzewo, którego
węzłami są poszczególne atrybuty, gałęziami wartości
odpowiadające tym atrybutom, a liście tworzą poszczególne
decyzje. Na podstawie przykładowych danych wygenerowano
następujące drzewo:
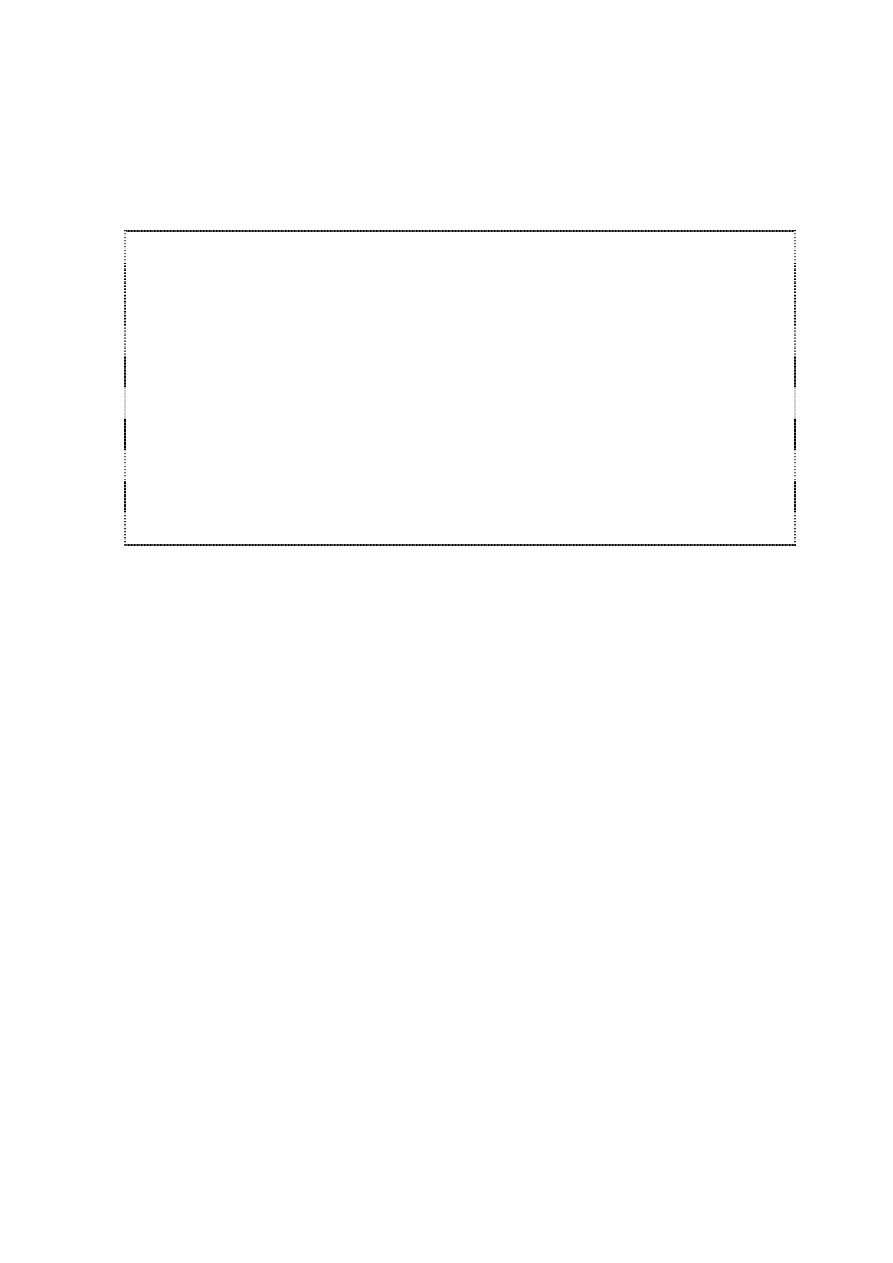
Rys. 49. Przykładowe drzewo decyzyjne stopnia trzeciego
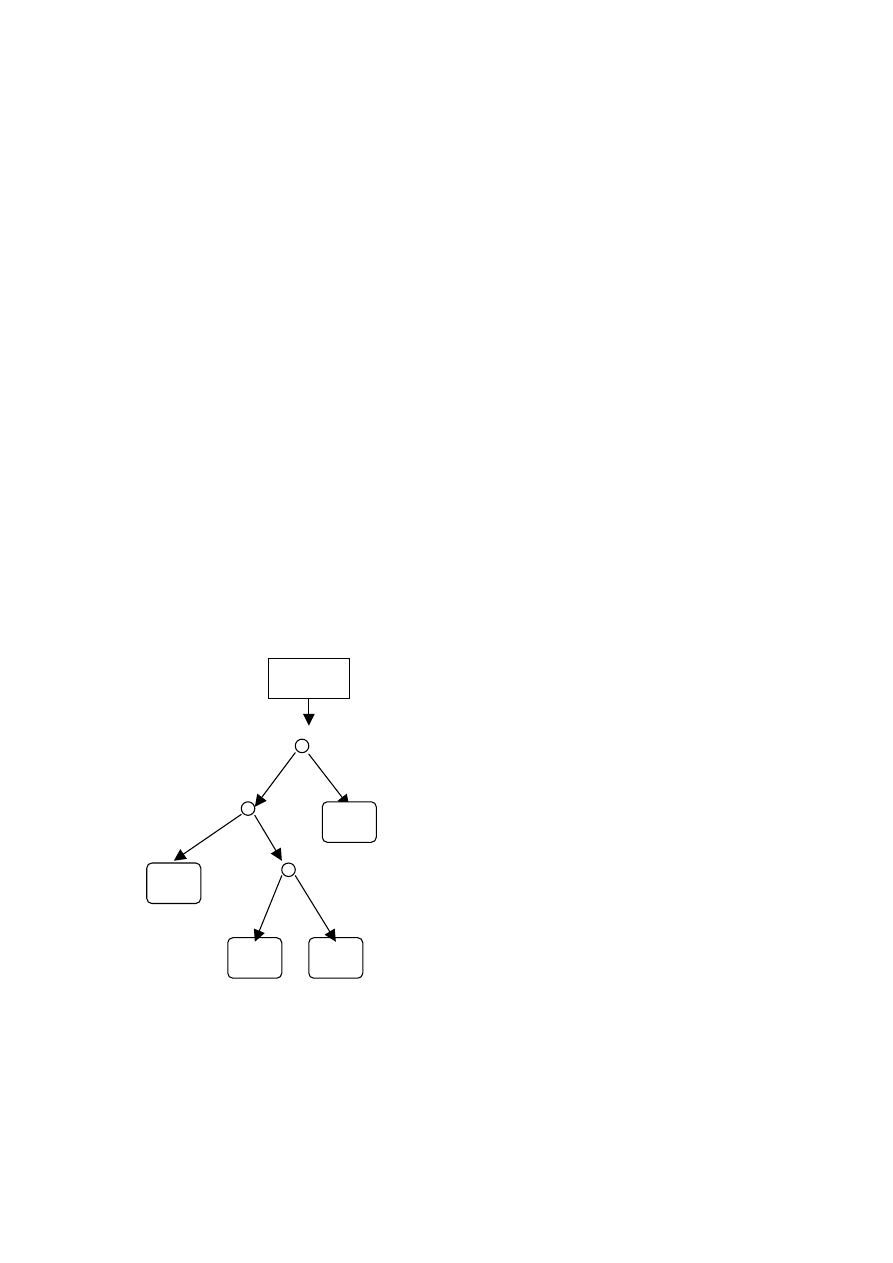
68
Drzewo w takiej postaci odzwierciedla, w jaki sposób na
podstawie
atrybutów
były
podejmowane
decyzje
klasyfikujące. Zaletą tej reprezentacji jest jej czytelność dla
człowieka. Łatwo tez zapisać algorytm klasyfikujący.
17. Wyrażenia kropkowe
Bardzo szczególną postacią drzew są drzewa przechowujące
tzw. wyrażenia kropkowe.
Reprezentantem wyrażenia kropkowego jest drzewo
binarne uzupełnione (w którym wszystkie węzły
wewnętrzne mają dwóch następników), posiadające
etykiety (wartości) tylko na liściach.
( ( a . ( b . c ) ) . d )
a) b)
Rys. 50 Przykład wyrażenia kropkowego: a) reprezentacja
w postaci drzewa, b) zapis „kropkowy”
root
a
c
b
d
69
Wyrażenia kropkowe mają dwa rodzaje węzłów: węzły
wewnętrzne bez etykiet (ich celem jest przechowanie
informacji o strukturze całego wyrażenia kropkowego), oraz
„normalne” węzły na liściach drzewa.
Możemy więc przy ich pomocy, na przykład:
• przedstawić strukturę rozgrywek piłkarskich:
( ( Wisła . ( Legia . Widzew ) ) . Amica )
• albo też przypisując węzłom kropkowym operatory
arytmetyczne, przedstawić strukturę wyrażenia
arytmetycznego: (( a * ( b + c )) – d ).
W pierwszym przykładzie, kropka pełnić może role
operatora wyłaniającego zwycięzcę lewego i prawego
argumentu, w drugim – operatora pozwalającego znaleźć
wartość wyrażenia arytmetycznego lewego i prawego
argumentu. Jest to więc bardzo wygodna, w pełni dynamiczna,
forma przechowywania informacji o strukturze.
K o n i e c c z ę ś c i 4