90
Implementacja algorytmu z powrotami w postaci drzewa
Drzewo jest właściwą strukturą do przechowania informacji o
możliwych drogach poszukiwania rozwiązania za pomocą
algorytmu z powrotami.
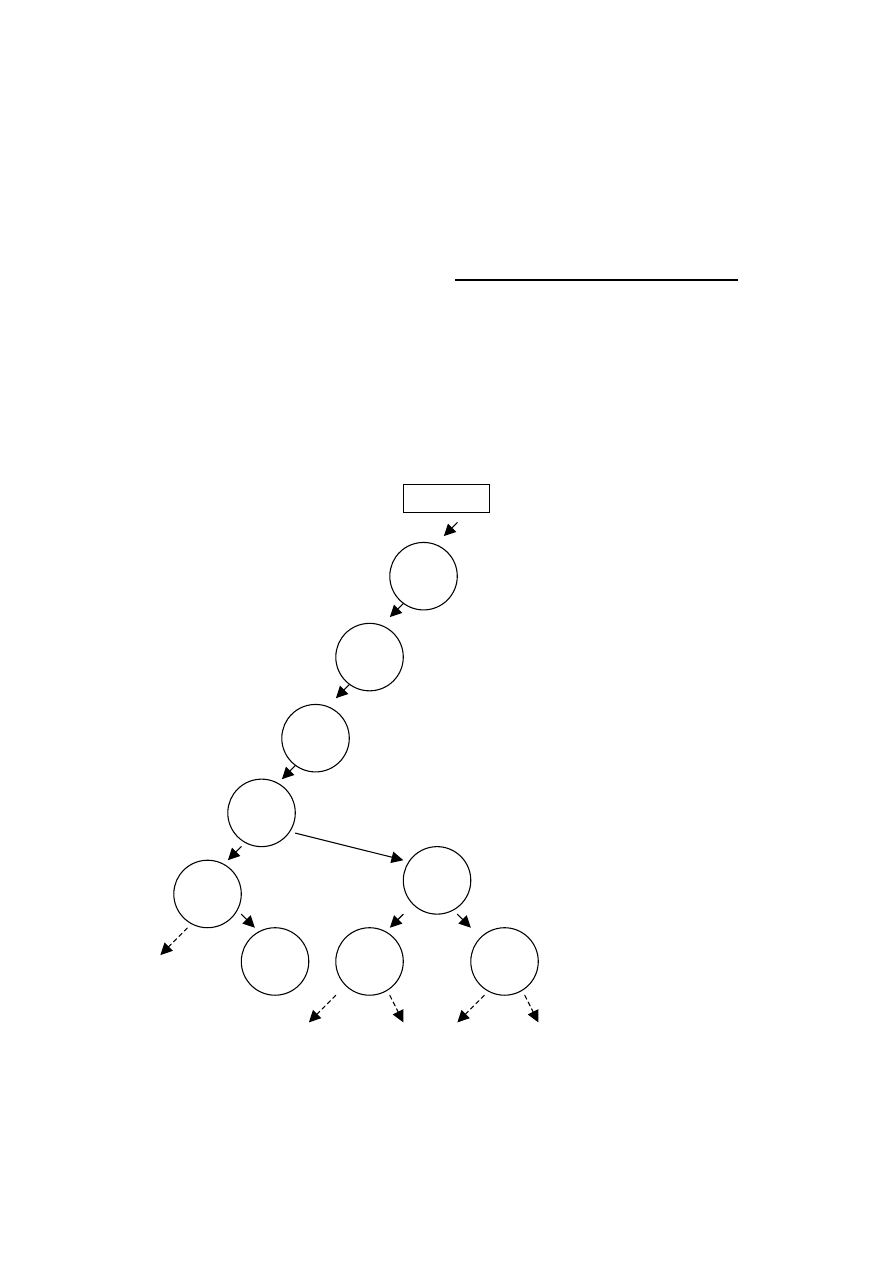
Poniższy rysunek przedstawia początkową część drzewa, tak
zwanego drzewa poszukiwań, w którym wszystkie możliwe
ścieżki zaczynające się od korzenia drzewa są możliwymi
drogami w labiryncie, zaczynającymi się od pola o numerze 1.
Jest to drzewo stopnia czwartego.
Znając wszystkie zbiory S
i
stosunkowo łatwo jest napisać
rekurencyjny algorytm generujący takie drzewo.
Rys.49 Początkowa część drzewa poszukiwań dla labiryntu z
rys. 47, gdy polem wyjściowym jest pole o numerze 1
labirynt
2
6
1
7
12
14
11
13
18
91
Ponieważ drzewo takie przedstawia wszystkie możliwe
ścieżki, jego rozległość, a więc i zajętość pamięci, jest
znaczna. Natomiast niewątpliwą zaletą takiej reprezentacji jest
możliwość przeglądania drzewa przy użyciu prostych metod,
na przykład – rozszerzonej metody preorder, w której liczba
wywołań rekurencyjnych, jak również głębokość rekurencji,
będzie zaledwie równa głębokości drzewa.
Jest oczywistym, że kształt drzewa, będzie zależał od
uporządkowania wartości w poszczególnych zbiorach S
i
,
powinniśmy więc przyjąć uporządkowanie generujące drzewo
o możliwie małej wysokości, co zniweluje głębokość rekursji
dla algorytmu przeglądającego drzewo.
Pojedyncze drzewo poszukiwań pozwala badać jedynie
ścieżki rozpoczynające się w punkcie umieszczonym w
korzeniu drzewa. Dlatego dla pełnej reprezentacji labiryntu
musimy utworzyć las zawierający drzewa rozpoczynające się
od wszystkich punktów labiryntu. Aby więc można było
stosować algorytm pozwalający badać ścieżki między dwoma
dowolnymi polami labiryntu musimy dysponować strukturą
zajmującą ogromny obszar pamięci.
Ponieważ zajętość pamięci rośnie tutaj wykładniczo ze
wzrostem rozmiarów labiryntu, dla większych labiryntów
stosowanie reprezentacji opartej o drzewa może okazać się
niemożliwe. Dla porównania – zajętość pamięci przy
wykorzystaniu reprezentacji w postaci zbiorów jest dla
naszego labiryntu nie większa niż 25 x 4 słowa pamięci, a co
najważniejsze rośnie liniowo ze wzrostem liczby pól
labiryntu. Pozostaje problem złożoności czasowej.
92
Ćwiczenia do samodzielnego rozwiązania:
1. Dlaczego stopień drzewa poszukiwań z rys. 49 wynosi
cztery ?
2. Czy drzewo poszukiwań z rys. 49 zawiera powtarzające
się węzły, i dlaczego ?
3. Czy oprócz metody preorder do przeglądania drzewa z
rys. 49 użyć można innych metod (inorder, postorder)
a jeśli tak, to w jakich sytuacjach byłoby to
uzasadnione?
4. Zaproponuj rekurencyjne algorytmy oparte o schemat
preorder:
a) tworzący drzewo poszukiwań dla danego punktu
początkowego na podstawie
danych zbiorów S
i
,
b) obliczający ilość wszystkich możliwych ścieżek
między zadanym punktem początkowym a
końcowym,
c) podający długość najkrótszej ścieżki między
zadanym punktem początkowym a końcowym,
wykorzystując wygenerowane drzewo
poszukiwań.
Metody usprawniania algorytmów o dużej złożoności
czasowej
Cały
szereg
dotychczas
poznanych
algorytmów
charakteryzowało się wykładniczą złożonością czasową. Były
to
algorytmy,
w
których
czas
obliczeń
wzrastał
nieprawdopodobnie szybko ze wzrostem rozmiarów struktury,
93
której dotyczyły. Związane to było najczęściej z użyciem
rekurencji. Przypomnijmy w tym miejscu takie algorytmy, jak:
rekurencyjny algorytm obliczający n-tą liczbę Fibonacciego,
algorytm sortowania szybkiego, algorytm szukania w głąb dla
grafu, ogólny algorytm z powrotami.
Duże zapotrzebowanie na czas obliczeń całkowicie
uniemożliwia
stosowanie
takich
algorytmów
do
rozwiązywania problemów, których rozmiary są dość znaczne.
Na szczęście wiele konkretnych problemów posiada
specyfikę, pozwalającą na usprawnienie algorytmów, które
dotychczas podawaliśmy w „czystej” postaci.
Ogólnie metody usprawniania algorytmów o dużej
złożoności czasowej dzielimy na dwie duże grupy:
- metody systematyczne,
- metody heurystyczne.
W kolejnych rozdziałach postaramy się przybliżyć na czym
metody
te
polegają,
opierając
się
na
wybranych,
charakterystycznych przykładach.
Metody systematyczne
Cechą charakterystyczną metod systematycznych jest
pewność. Ich stosowanie nie wpływa na jakość algorytmu, w
szczególności:
nie
zmniejsza
szans
na
znalezienie
rozwiązania, w niczym nie ogranicza ilości rozwiązań, czy ich
dokładności.
Istnieje bardzo dużo różnego rodzaju metod usprawniania
algorytmów w sposób systematyczny. Prawie zawsze zależą
on od specyfiki rozwiązywanego problemu. W niniejszym
rozdziale omówimy trzy najczęściej spotykane metody.
94
Metoda obcinania gałęzi
Metoda ta polega, mówiąc ogólnie, na rezygnacji z pewnych
dużych obszarów potencjalnych rozwiązań w oparciu o
stwierdzenia zaprzeczające istnieniu rozwiązań w tych
obszarach.
Jeśli problem byłby przedstawiony w postaci drzewa (
takiego jak drzewo poszukiwań ), to obcinanie gałęzi będzie
polegać na zaniechaniu poszukiwań w gałęzi ( poddrzewie )
zaczynającym się od określonego węzła. Można tego dokonać
tylko wtedy, jeśli mamy uzasadnioną pewność, że wybór tego
węzła i wszystkich jego następników nie prowadzi do
rozwiązań.
Do jak dużych usprawnień algorytmu może prowadzić
metoda obcinania gałęzi pokażemy posługując się klasycznym
przykładem tak zwanego problemu ośmiu hetmanów.
Problem ten sprowadza się do odpowiedzi na pytanie:
Na ile różnych sposobów można ustawić na szachownicy o
rozmiarach 8 x 8 osiem hetmanów, aby się wzajemnie nie
szachowały ?
Algorytm rozwiązania tego problemu w „czystej” postaci, to
jest opartej tylko na regułach szachowania, wymaga dla n=8
astronomicznej liczby badań ≅
≅
≅
≅ 4.4 x 10
9
.
Stosując metodę obcinania gałęzi wykluczymy przede
wszystkim takie ustawienia hetmanów, które zawierają dwie
figury w tym samym wierszu, w tej samej kolumnie, na tej
samej przekątnej. Taka eliminacja ogranicza liczbę ustawień
do zbadania do 2056 ustawień.
95
Metoda sklejania gałęzi
Metoda sklejania (łączenia) gałęzi jest kolejnym przykładem
metody systematycznej. Jeśli szukamy pewnych rozwiązań a
w
drzewie
poszukiwań
istnieje
więcej
poddrzew
izomorficznych (takich samych jak badane poddrzewo), to
wystarczy zbadać tylko jedno, a otrzymany wynik
wykorzystać w innych miejscach wystąpienia takiego
poddrzewa.
Okazuje się, że zastosowanie metody sklejania gałęzi do
algorytmu rozwiązującego problem ośmiu hetmanów, jako
kolejnej
metody
systematycznej
po
wcześniejszym
zastosowaniu metody obcinania gałęzi, pozwala zredukować
liczbę badań już tylko do 801 węzłów.
Metoda dekompozycji
Wśród metod systematycznych szczególnie ważną pozycje
zajmuje metoda zwana metodą dekompozycji problemu, lub
metodą „dziel i zwyciężaj”. Jej zasadnicza idea została
zastosowana w omawianym już algorytmie sortowania
szybkiego Quick Sort dla tablic.
Ogólnie mówiąc polega ona na rozłożeniu rozwiązywane
problemu na k podproblemów ( jeśli jest to oczywiście
możliwe ), rozwiązaniu każdego z nich, a następnie
połączeniu rozwiązań cząstkowych w jedną całość. Wzrasta
wtedy zapotrzebowanie na pamięć, trzeba bowiem gdzieś
przechowywać rozwiązania cząstkowe przed ich zcaleniem,
ale może prowadzić do znacznego skrócenia czasu obliczeń.
96
Załóżmy, że rozwiązanie wymaga czasu C * 2
n
, gdzie n jest
rozmiarem zadania, a C - pewną stałą. Po zastosowaniu
dekompozycji czas obliczeń skraca się do k *C * 2
n/k
+ T,
gdzie T jest czasem potrzebnym na połączenie wszystkich
rozwiązań cząstkowych. Jeśli k nie jest duże i połączenie nie
jest zbyt kosztowne, metoda ta może dać znaczne skrócenie
czasu obliczeń.
Metody heurystyczne
Metody heurystyczne stosujemy, gdy nie ma możliwości
posłużenia się metodami systematycznymi. Idea tych metod
polega na przyjęciu pewnych założeń, co do których nie
mamy pewności, lub nawet wiemy, że nie są słuszne w całym
obszarze działania algorytmu, ale które bardzo wspomagają
poszukiwanie rozwiązań. Postępujemy tak mając świadomość,
że w pewnych, chociaż mniej prawdopodobnych sytuacjach,
zastosowana metoda heurystyczna może utrudnić szybkie
znalezienie rozwiązania, a czasem nawet uniemożliwić w
ogóle jego znalezienie.
Po metody heurystyczne będziemy więc sięgać, gdy nie
zależy nam na znalezieniu wszystkich rozwiązań i możemy
zadowolić się jednym rozwiązaniem, które jednak musi być
znalezione bardzo szybko (typowa sytuacja z gier
komputerowych).
W innych jeszcze przypadkach, gdy istnienie rozwiązań jest
bardzo wątpliwe, warto skorzystać z metod heurystycznych i
być może w krótkim czasie znaleźć jakieś rozwiązanie.
Jest bardzo wiele rozwiązań heurystycznych, tak jak wiele
jest różnych typów algorytmów wymagających usprawnienia.
97
W odniesieniu do algorytmu poszukującego drogi w
labiryncie od pola a do pola b, jeśli wartość a jest mała, a
wartość b duża, stosowanie heurystyki mogłoby polegać na
ustawieniu wartości we wszystkich zbiorach S
i
w porządku
malejącym.
W ten sposób zapewnilibyśmy wybory pól o dużych
wartościach
w
pierwszej
kolejności
i
większe
prawdopodobieństwo poruszania się po krótszej ścieżce a co
za tym idzie – szybsze osiągnięcie celu. Przyjmując taką
heurystykę musimy mieć świadomość, że przy pewnych
szczególnych ograniczeniach, występujących w labiryncie,
przyjęcie takiej heurystyki może utrudnić znalezienie
rozwiązania.
Szacowanie złożoności obliczeniowej algorytmów
Wykonanie każdego algorytmu wymaga określonego czasu
pracy komputera i określonej ilości pamięci.
Jak to już podkreślaliśmy, dla pewnych klas algorytmów,
czas ich działania lub rozmiar potrzebnej pamięci zwiększa się
bardzo szybko ze wzrostem rozmiaru zadania. Pojęcie
rozmiaru zadania, jak również innych pojęć, zdefiniujemy
sobie w dalszej części tego rozdziału dokładniej. Na razie
założymy, są one albo intuicyjnie dość zrozumiałe, albo ich
znaczenie zostało już wcześniej zasygnalizowane.
Załóżmy, że dysponujemy komputerem, który pracuje bez
przerwy przez 24 godz. wykonując tylko 10
5
operacji
jednostkowych na sekundę.
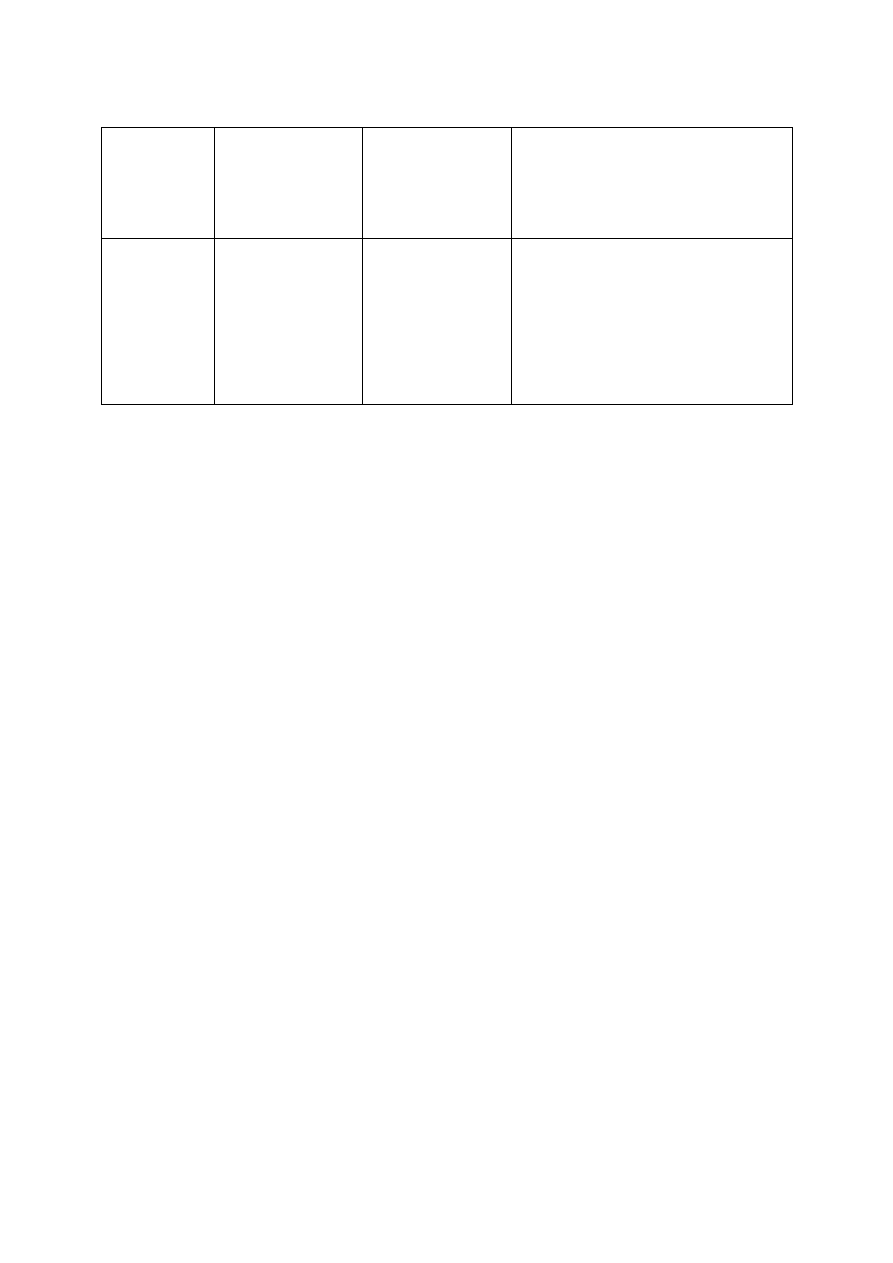
98
Algorytm
Klasa
algorytmu
Maksymalny
rozmiar
zadania
Maksymalny rozmiar
zadania
po 10-krotnym zwiększeniu
szybkości
A
1
A
2
A
3
A
4
A
5
A
6
O(N)
O(N*log N)
O(N
2
)
O(N
3
)
O(2
N
)
O(N!)
n
1
=864*10
7
n
2
=250*10
6
n
3
=900*10
2
n
4
=200*10
1
n
5
= 33
n
6
= 13
10* n
1
ok. 10* n
2
dla n
2
>>1
3.16* n
3
2.15* n
4
n
5
+ 3.3
-
Rys. 50 Tabela maksymalnych rozmiarów zadania, które można
rozwiązać w czasie 24 godz. dysponując algorytmami
różnych klas.
Trzecia kolumna powyższej tabeli pokazuje, jakie mogą być
maksymalne rozmiary zadania, które można rozwiązać w
czasie 24 godz. dla algorytmów różnych klas. Ostania
kolumna natomiast, jak zwiększy się maksymalny rozmiar
zadania po 10-krotnym zwiększeniu szybkości obliczeń przez
komputer.
Wyniki zamieszczone w tej tabeli pozwalają ocenić, jak
ważną sprawą jest dysponowanie algorytmem odpowiedniej
klasy. Widać, że dostatecznie satysfakcjonujące są algorytmy
klasy O(N) i O(N * log N), niestety bardzo często zmuszeni
jesteśmy sięgać po algorytmy klasy O(N
2
).
Szokująco niskie wyniki dają natomiast algorytmy A
5
i A
6
, to
jest algorytmy o wykładniczej złożoności obliczeniowej.
Trzeba tu bowiem aż całej doby, aby doczekać się na wynik
działania algorytmu, gdy rozmiar rozwiązywanego zadania
wynosi zaledwie kilkadziesiąt, lub nawet kilkanaście.
99
Ostania kolumna tej tabeli uzmysławia nam, że rozwój
sprzętu (coraz szybsze procesory i pamięci) niewiele
poprawiają sytuację, zwłaszcza dla algorytmów o dużej
złożoności obliczeniowej, dla których maksymalny rozmiar
zadania nawet nie wzrasta liniowo ze wzrostem mocy
obliczeniowej (algorytm A
5
), lub nawet jest tak mały, że
trudno go uchwycić (algorytm A
6
).
Tak
więc
ogromny
postęp
w
rozwoju
sprzętu
komputerowego, jaki cały czas obserwujemy, nie wpłynie w
zasadniczy sposób na czas obliczeń, jeśli do rozwiązywania
problemów stosować będziemy nieodpowiednie algorytmy.
Rola
algorytmiki,
dziedziny
informatyki
teoretycznej,
zajmującej się opracowywaniem nowych algorytmów i
doskonaleniem już istniejących, jest ogromna.
Odwróćmy teraz sytuacje i załóżmy, że dysponujemy
komputerem, który wykonuje 10
6
operacji jednostkowych na
sekundę i podajmy czasy wykonywania się programów
opartych o algorytmy różnych klas, gdy rozmiary zadania
wynoszą: 10, 20 i 30.
Algorytm
Klasa
algorytmu
N=10
N=20
N=30
A
1
A
2
A
3
A
4
A
5
A
6
O(N)
O(N
2
)
O(N
3
)
O(2
N
)
O(3
N
)
O(N!)
1*10
-5
sek
1*10
-4
sek
1*10
-3
sek
1*10
-3
sek
0.59 sek
3.6 sek
2*10
-5
sek
4*10
-4
sek
8*10
-3
sek
1 sek
58 min
768 wieków
3*10
-5
sek
9*10
-5
sek
2.7*10
-2
sek
17.9 min
6.5 lat
8.4 *10
16
wieków
Rys. 51 Czasy wykonywania się programów oparte o algorytmy
różnych klas.
100
Wyniki zamieszczone w tej tabeli potwierdzają wnioski
wynikające z analizy wyników zamieszczonych w poprzedniej
tabeli i jeszcze bardziej utwierdzają w przekonaniu, że
sięganie
po
algorytmy
o
wykładniczej
złożoności
obliczeniowej dla zadań o rozmiarze przekraczającym
kilkanaście mija się z celem.
Uściślimy teraz, stosowane dotychczas w sposób dość
intuicyjny, pojęcia. Zobaczymy też, jak w prosty sposób, nie
uciekając się do rozbudowanego aparatu matematycznego,
szacować można złożoność obliczeniową algorytmów.
Następujące operacje, zapisane w języku wysokiego
poziomu, uważać będziemy dla celów szacowania złożoności
obliczeniowej, za operacje jednostkowe:
- wykonanie operatora numerycznego, relacyjnego lub
logicznego,
- nadanie wartości zmiennej typu prostego,
- obliczenie
wartości
zmiennej
indeksowanej,
wskazywanej lub pola struktury,
- inicjowanie procedury lub funkcji,
- przekazanie wartości parametru aktualnego,
- wykonanie operacji wejścia lub wyjścia.
Dla celów szacowania złożoności obliczeniowej założyć
można, że czas wykonywania wszystkich tych operacji jest
taki sam.
Załóżmy teraz, że mamy algorytm K, dla którego dla
każdego zestawu danych wejściowych d ∈
∈
∈
∈D (D jest zbiorem
zestawów danych wejściowych), obliczenia algorytmu
dochodzą do punktu końcowego. Przez T(d) oznaczać
101
będziemy liczbę operacji jednostkowych wykonywanych
przez algorytm K dla d ∈
∈
∈
∈D. Funkcję T(d) nazywamy pełną
funkcją kosztu.
Jest to funkcja T: D →
→
→
→ N ze zbioru danych wejściowych w
zbiór liczb naturalnych (liczbę operacji jednostkowych).
Zwykle bardzo trudno jest ustalić i opisać pełną funkcję
kosztu, jest ona bowiem trudna do wyznaczenia i zapisania w
jednolity, czytelny sposób dla każdego z możliwych zestawów
danych wejściowych.
Z powyższych powodów określamy zwykle tylko rząd
wielkości funkcji. Z praktycznego punktu widzenia jest
zresztą niecelowe wyznaczanie pełnej funkcji kosztu.
Niewiele informacji daje nam bowiem opis zachowania się
algorytmu w sytuacjach najlepszego przypadku, czy nawet
średnie zachowanie się algorytmu.
Natomiast interesujące są sytuacje najgorszego przypadku,
gdyż tutaj tkwi niebezpieczeństwo znacznego wydłużenia
czasu obliczeń. Określmy teraz pojęcie rzędu funkcji. Niech X
będzie dowolnym zbiorem. Dysponujemy dwiema funkcjami
f: X →
→
→
→ R oraz g: X →
→
→
→ R.
Definicja: Powiemy, że funkcja f jest co najwyżej rzędu
funkcji g, co zapiszemy f=O(g), jeśli istnieje stała
c>0, takie że relacja |f(x)| ≤
≤
≤
≤ c * |g(x)| zachodzi dla
prawie wszystkich wartości x ∈
∈
∈
∈X (to jest dla
wszystkich, za wyjątkiem pewnego, niewielkiego,
skończonego, być może pustego, podzbioru X).
Tym niewielkim, skończonym podzbiorem będą, w
przypadku szacowania złożoności obliczeniowej, te zbiory
102
danych, dla których pełna funkcja kosztu T(d) nie da się
dokładnie oszacować przez jakąś prostą funkcję g(N).
Sytuacja ta zresztą dotyczy zwykle niewielkich wartości N, a
ponieważ jesteśmy zainteresowani szacowaniem złożoności
obliczeniowej dla dużych N, możemy pominąć te niewielkie
zbiory danych wejściowych i szacować T(d) przez g(N) jako
O(g(N))
mówiąc
o
funkcji
kosztu
niepomyślnego
przypadku lub po prostu o funkcji kosztu. W literaturze
spotkać można jeszcze inne określenia dla funkcji kosztu:
funkcja złożoności czasowej (lub złożoność czasowa),
pesymistyczna złożoność czasowa, klasa algorytmu.
Teraz zdefiniujemy sobie pojęcie rozmiaru danych.
Ponieważ uzależnianie funkcji kosztu od wszystkich danych
komplikuje sprawę konstruowania tej funkcji, wyróżnia się
spośród danych te, które mają największy wpływ na wartość
funkcji kosztu.
Na przykład, w algorytmie wykonującym mnożenie
macierzy, gdzie D = < A, B, m, n, k >, macierz A ma rozmiar
m*n a macierz B ma rozmiar n*k, wpływ na funkcje kosztu
mają tylko rozmiary obu macierzy, to jest m, n i k.
Chociaż w szeregu algorytmów również postać samych
danych (ich wartość, sposób uporządkowania, itd.) wpływa na
czas działania algorytmów, dla algorytmu mnożenia macierzy
można przyjąć, że rozmiarem danych, oznaczmy go przez |d|,
jest |d|=max(m,n,k).
Algorytm mnożenie macierzy jest jednak algorytmem pod
tym względem trochę nietypowym. Na ogół łatwo jest
określić, co jest rozmiarem danych. Są to: rozmiar
103
jednowymiarowej tablicy, liczba elementów w liście liniowej
jednokierunkowej, liczba węzłów w drzewie, lub jego
wysokość, liczba węzłów i/lub liczba krawędzi w grafie.
Podobnie, przy szacowaniu złożoności obliczeniowej
algorytmów rozważa się tylko pewne wyróżnione operacje
jednostkowe, zwane operacjami dominującymi algorytmu.
W algorytmach wykorzystujących iterację są to zwykle
warunki kontrolujące pętle iteracyjne. Ilość wykonanych
badań takiego warunku jest w przybliżeniu równa ilości
wykonań wnętrza pętli iteracyjnej.
Instrukcje wewnętrzne pętli, o ile same nie są pętlami lub
wywołaniami iteracyjnymi, nie mają wpływu na szacowanie
kosztu algorytmu, bowiem od ich ilości zależy tylko wartość
stałej przez którą mnożymy ilość wykonań pętli. Ponieważ
wyznaczamy tylko rząd funkcji, nie ma to żadnego znaczenia
dla szacowania złożoności czasowej algorytmu.
Tak więc otrzymaliśmy bardzo prosty przepis na szacowania
złożoności obliczeniowej algorytmów iteracyjnych pod
warunkiem, że potrafimy dobrze zidentyfikować rozmiar
danych a także wskazać wszystkie operacje dominujące
algorytmu. O wiele trudniej jest szacować funkcje kosztu dla
algorytmów rekurencyjnych. To jednak przekracza ramy
naszego wykładu.
Poniższy przykład zilustruje, jak szacować złożoność
obliczeniową algorytmów iteracyjnych. Zadanie polega na
oszacowaniu funkcji kosztu dla algorytmu na podstawie
fragmentów programu, zapisanego w języku C++.
104
. . . . .
int a[N];
. . . . .
for (int i:=2; i<= n; i++)
1: if (a[i-1]>a[i]) then
{
v:=a[i]; j:=i-1;
do
{ a[j+1]:=a[j]; j:=j-1; }
2: while( a[j] <= v );
a[j+1]:=v;
}
Badanie warunku zapisanego w linii 1 wykona się dokładnie
n-1 razy, w linii 2 – co najwyżej i-1 razy (tzn. dla j=i-1, i-2,
..., 0). Tak więc ogólna liczba porównań jest ograniczona od
od góry przez
n
(i-1) + ∑
∑
∑
∑(i-1) = n-1 + n*(n+1)/2 –1 – (n-1) = = 0.5*n
2
+ 0.5*n – 1
i=2
Ponieważ otrzymana funkcja może być ograniczona przez
funkcję n
2
możemy stwierdzić, że złożoność obliczeniowa
tego algorytmu wynosi O(n
2
).
Na koniec tego rozdziału zdefiniujemy jeszcze w sposób
ostateczny pojęcia algorytmu o wielomianowej i wykładniczej
złożoności czasowej.
Definicja: Algorytmem wielomianowym nazywać będziemy
algorytm, którego funkcją złożoności czasowej jest
O(p(N)), gdzie p jest pewnym wielomianem a N –
rozmiarem danych.
Definicja: Każdy algorytm, którego funkcja złożoności
czasowej
nie
może
być
ograniczona
105
wielomianem,
nazywamy
algorytmem
wykładniczym (chociaż jego funkcja złożoności
czasowej
niekoniecznie
musi
być
funkcją
wykładniczą).
Ćwiczenia do samodzielnego rozwiązywania:
1. Spróbuj oszacować funkcje złożoności obliczeniowej dla
algorytmów omówionych w treści wykładu.
Problemy algorytmicznie trudne
Już od bardzo dawna ludzie zajmujący się algorytmami
starali się odpowiedzieć sobie na pytanie:
Czy dla problemów, dla których nie znaleziono dotychczas
rozwiązujących je w wielomianowym czasie algorytmów,
takie algorytmy w ogóle istnieją ?
Dzisiaj można stwierdzić, że odpowiedź na to pytanie jest
bardzo złożona.
Wszystkie omówione w trakcie wykładu algorytmy
rozwiązywały problemy należące do wielkiej rodziny
problemów, nazwanej problemami decyzyjnymi. Odrębna
rodzinę stanowią, na przykład, problemy zwane problemami
optymalizacyjnymi.
Problemami
z
tego
zakresu
nie
zajmowaliśmy się.
Klasę problemów decyzyjnych nazwano NP. W klasie tej
zawarta jest klasa problemów nazwana klasą P.
Definicja: Klasę problemów P tworzą wszystkie problemy
decyzyjne, dla których istnieją rozwiązujące je w
wielomianowym czasie algorytmy.
106
Najbardziej interesującą klasą jest klasa tzw. problemów NP
– zupełnych, do której należą klasycznie trudne problemy
decyzyjne i dla których, mimo usiłowań, nie udało się znaleźć
algorytmów wielomianowych. Prawdopodobnie można je
rozwiązywać tylko przy pomocy algorytmów wykładniczych.
Aktualna lista problemów NP – zupełnych obejmuje już kilka
tysięcy problemów z różnych dziedzin.
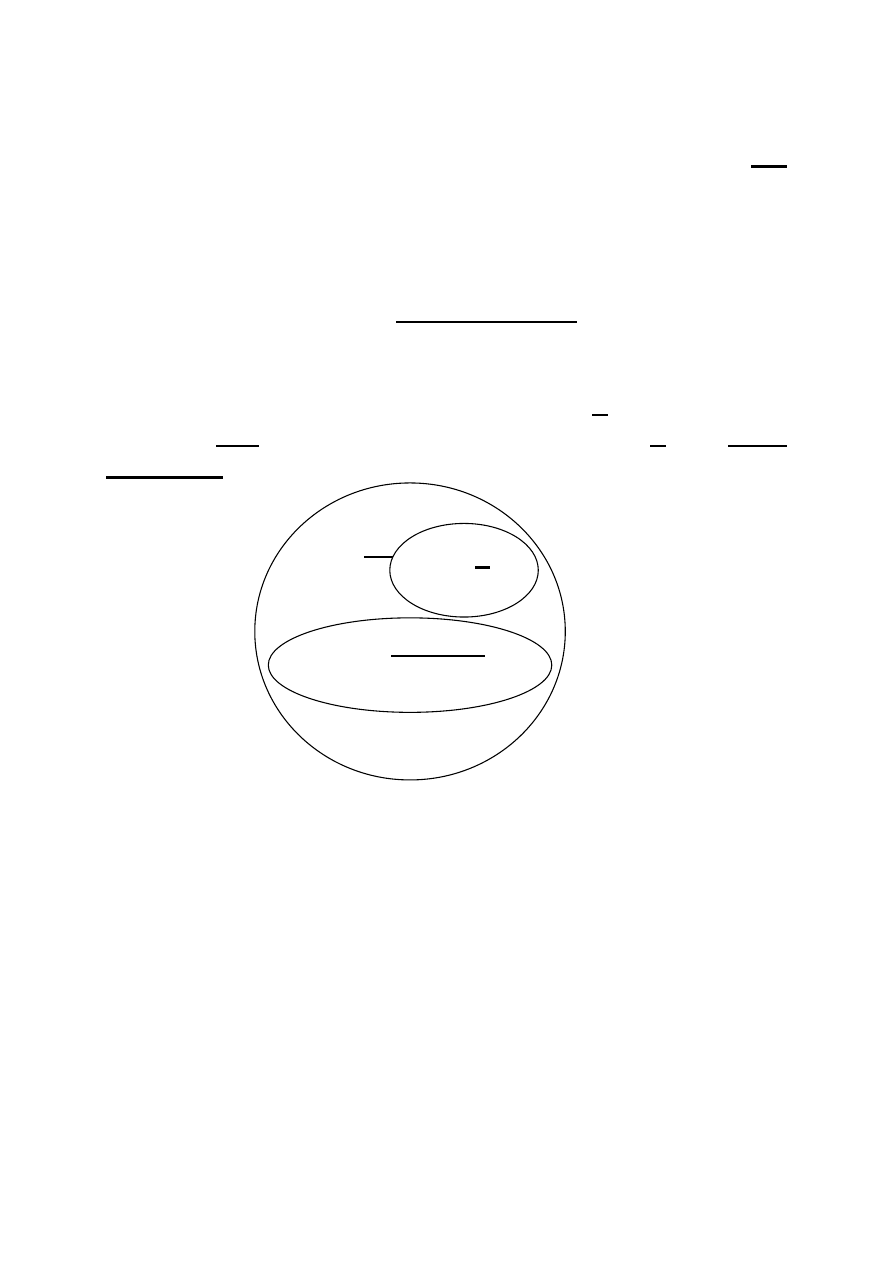
Oznaczałoby to, że klasa problemów P jest właściwą
podklasą NP, a ponadto, że klasy problemów P i NP -
zupełnych są rozłączne.
Rys. 52 Podział klas problemów z punktu widzenia istnienia dla nich
algorytm wielomianowych.
klasa NP klasa P
problemy NP- zupełne