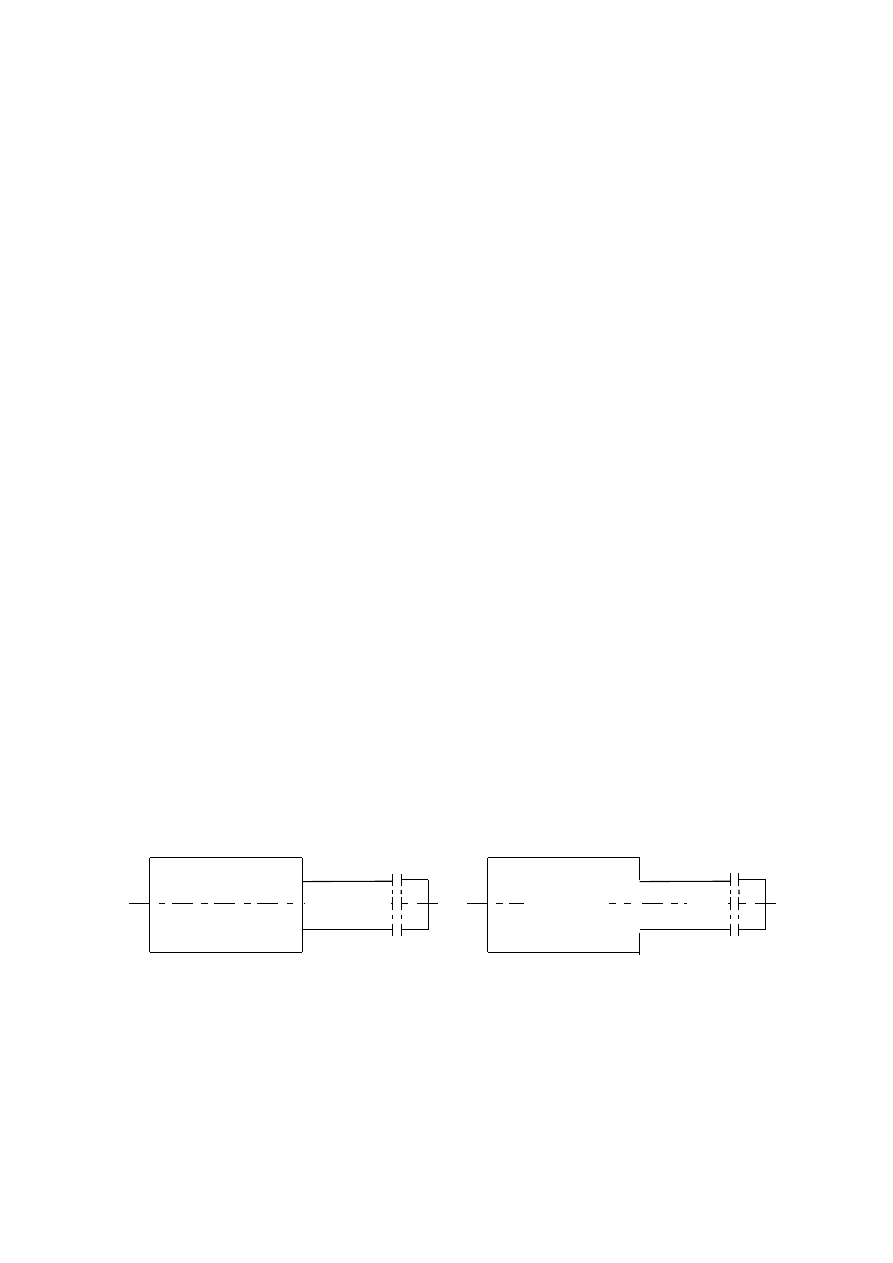
Zadanie 1.10
W celu wyznaczenia zasobu objętości V
r
rurociągu połączono go ze zbiornikiem o zasobie
objętości V
z
=5[m
3
]. Zbiornik przed połączeniem z rurociągiem zawierał powietrze o
parametrach stanu p
z1
=0,6[MPa], t
z1
=20[
0
C], w rurociągu zaś parametry stanu powietrza były
odpowiednio równe p
r1
=0,1[MPa], t
r1
=15[
0
C]. Po połączeniu i wyrównaniu temperatur oraz
ciśnień w układzie zbiornik-rurociąg zmierzono wartości ciśnienia p
r2
=0,22[MPa] i
t
r2
=16[
0
C]. Wyznaczyć a następnie obliczyć wartość zasobu objętości rurociągu V
r.
Rozwiązanie:
Dane:
Wyznaczyć a następnie obliczyć wartość:
V
z
=5[m
3
]
V
r
p
z1
=0,6[MPa]
t
z1
=20[
0
C]
p
r1
=0,1[MPa]
t
r1
=15[
0
C]
p
r2
=0,22[MPa]
t
r2
=16[
0
C].
1. Ilustracja układu zbiornik-rurociąg przed i po ich połączeniu.
2. Wyznaczenie zasobu masy gazu w zbiorniku przed połączeniem go z rurociągiem.
Z równania stanu gazu doskonałego Clapeyrona
p
z1
V
z
=m
z1
RT
z1
V=V
z
+V
r
p
r2
= p
z2
t
r2
= t
z2
V
r
p
z1
, t
z1
, V
z
p
r1
, t
r1
, V
r
wyznaczono zasób masy gazu w zbiorniku
m
z1
=
1
1
z
z
z
RT
V
P
3. Wyznaczenie zasobu masy gazu w zbiorniku po połączeniu go z rurociągiem.
Z równania stanu gazu doskonałego Clapeyrona po wyrównaniu się temperatur i
ciśnień w zbiorniku i rurociągu.
p
r2
V
z
=m
z2
RT
r2
wyznaczono zasób masy gazu w zbiorniku.
m
z2
=
2
2
r
z
r
RT
V
p
4. Wyznaczenie przyrostu zasobu masy gazu w zbiorniku.
Odejmując zasoby mas powietrza wzbiorniku przed i po połączeniu z rurociągiem
wyznaczono przyrost zasobu masy powietrza w zbiorniku.
∆ m
z
=m
z1
-m
z2
=
2
2
1
1
r
r
z
z
z
T
p
T
p
R
V
5. Wyznaczenie zasobu masy gazu w rurociągu przed dopływem gazu ze zbiornika.
Dzieląc stronami równanie stanu gazu doskonałego Clapeyrona dla rurociągu przed
dopływem gazu ze zbiornika.
p
r1
V
r
=m
r1
RT
r1
i po dopływie gazu ze zbiornika.
p
r2
V
r
=(m
r1
+∆m
z
)RT
r2
otrzymano związek
2
1
1
1
2
1
)
(
r
z
r
r
r
r
r
T
m
m
T
m
p
p
z którego wyznaczono zasób masy gazu w rurociągu przed dopływem gazu ze
zbiornika .
m
r1=
1
2
2
1
2
1
2
1
1
r
r
r
r
r
z
r
z
r
p
T
p
T
R
p
T
T
p
p
V
z
6. Wyznaczanie zasobu objętości rurociągu.
Zasób objętości rurociągu wyznaczono z równania stanu gazu doskonałego
Clapeyrona przed dopływem powietrza ze zbiornika.
V
r
=
1
2
2
1
2
1
2
1
1
1
1
1
r
r
r
r
r
z
r
z
r
z
r
r
r
p
T
p
T
p
T
T
p
T
V
p
RT
m
7. Rachunek mian dla zasobu objętości rurociągu.
[V
r
]=
3
3
)
(
)
(
m
KPa
KPa
Pa
Pa
K
m
8. Obliczenie wartości zasobu objętości rurociągu.
V
r
=
1
2
2
1
2
1
2
1
1
1
1
1
r
r
r
r
r
z
r
z
r
z
r
r
r
p
T
p
T
p
T
T
p
T
V
p
RT
m
452
,
15
10
)
1
,
0
)
15
,
273
16
(
22
,
0
)
15
,
273
15
((
10
22
,
0
15
,
273
20
15
,
273
16
6
,
0
)
15
,
273
15
(
5
6
6
[m
3
]
Zadanie 1.11
Wyznaczyć a następnie obliczyć wartość promienia cząsteczki tlenu O
2
przy założeniu, że
ma ona kształt kulisty i wiedząc że wartość molowej współobjętości
(objętości wyłączonej molowej) w równaniu stanu gazu rzeczywistego van der Waalsa jest
równa b=25[
mol
cm
3
], zaś liczba Avogadra N
A
=6,023∙10
23
[
mol
1
].
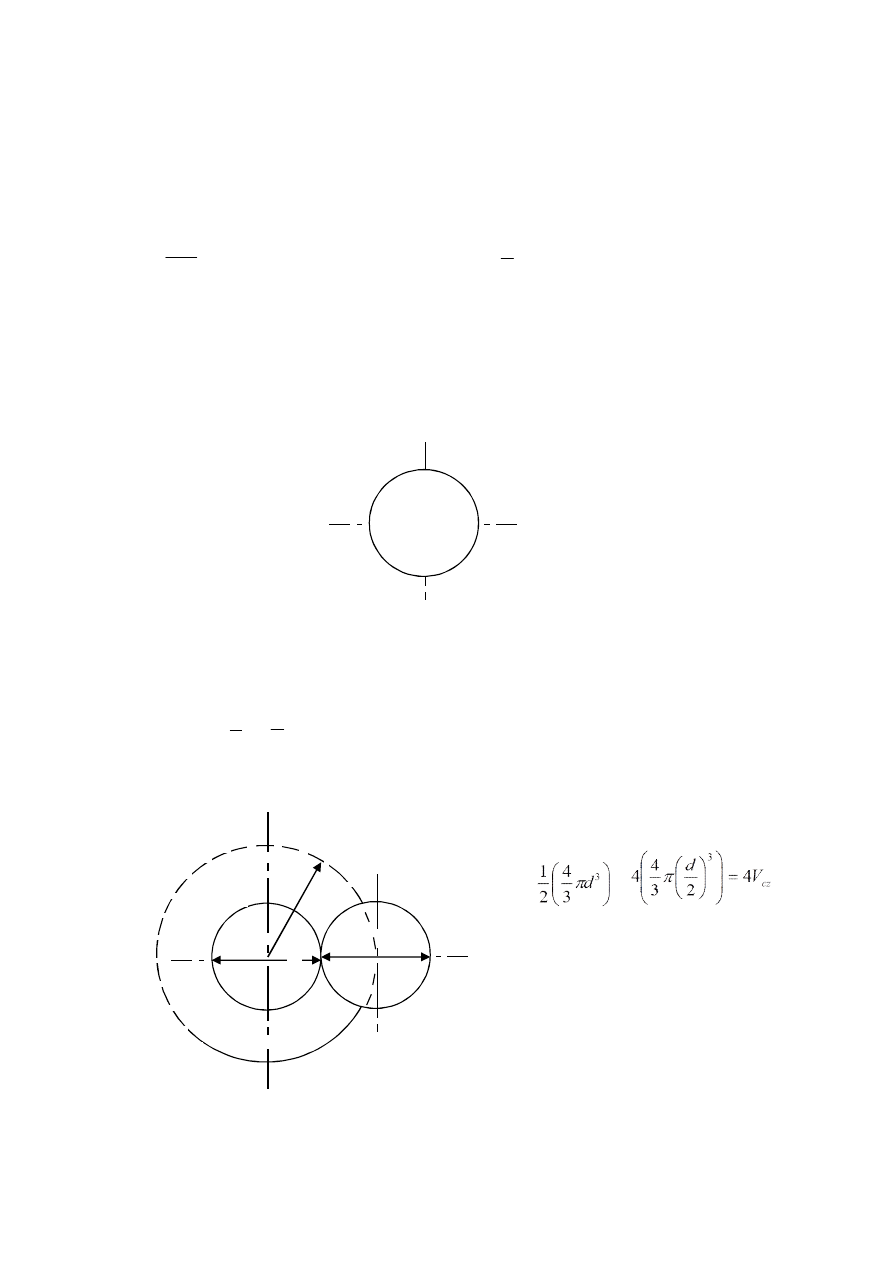
Rozwiązanie:
Dane:
Wyznaczyć a następnie obliczyć wartość:
b = 25 [
mol
cm
3
]
r =
2
d
N
A
= 6,023∙10
23
[mol
-1
]
1. Wyznaczanie objętości cząsteczki tlenu w kształcie kuli o średnicy d:
Ilustracja objętości cząsteczki tlenu O
2
w kształcie kuli o średnicy d.
V
cz
=
3
4
3
2
d
2. Wyznaczanie objętości wyłączonej dla cząsteczki tlenu.
Ilustracja objętości wyłączonej dla
cząsteczki tlenu O
2
d
V
w
=
=
d
d
d
Objętość wyłączona jest objętością w której środki cząsteczek nie mogą się poruszać ze
względu na swoją wzajemną obecność i równa jest połowie objętości kuli
o promieniu równym średnicy cząsteczki.
Objętość wyłączona zasobu ilości materii n=1[mol] cząsteczek (współobjętość
molowa) równa jest iloczynowi liczby Avogadra N
A
i objętości wyłączonej
cząsteczek V
w
b = N
A
V
w
[
mol
m
3
]
3. Wyznaczenie równania stanu gazu rzeczywistego van der Waalsa odniesionego do
molowych gęstości zasobu energii.
Równanie stanu gazu rzeczywistego van der Waalsa odniesione do masowych gęstości
zasobu energii określone jest związkiem:
(p+
2
a
)(-) = RT
gdzie:
a – współczynnik kohezyjności masowej
– współobjętość masowa (kowolumen)
Współczynnik kohezyjności masowej określony jest zależnością:
a =
2
M
a
n
gdzie:
n
a – współczynnik kohezyjności molowej
M – masa cząsteczkowa
Ciśnienie kohezyjne określone jest wyrażeniem
2
a
natomiast współobjętość masowa jest równa:
=
M
b
gdzie:
b – współobjętość molowa (objętość wyłączona molowa).
zatem równanie van der Waalsa przekształcono do postaci:
[p +
2
2
M
a
n
](-
M
b
) = RT
Relacja między masową a molową gęstością zasobu objętości określona jest zależnością:
=
M
n
stąd równanie stanu gazu rzeczywistego van der Waalsa przyjmie postać:
(p+
2
n
n
a
)(
M
n
-
M
b
) = RT
Uwzględniając, iż iloczyn indywidualnej stałej gazowej i masy cząsteczkowej równy jest
uniwersalnej stałej gazowej:
MR = B
oraz mnożąc obustronnie równanie van der Waalsa przez masę cząsteczkową M otrzymamy
równanie stanu gazu rzeczywistego van der Waalsa odniesione do molowych gęstości zasobu
energii
(p+
2
n
n
a
)(
n
-b) = BT
4. Wyznaczanie promienia cząsteczki tlenu.
Dzieląc objętość wyłączoną molową cząsteczek b przez liczbę Avogarda N
A
otrzymano objętość wyłączną cząsteczki O
2
tlenu.
V
w
=
A
N
b
Z drugiej strony objętość wyłączoną cząsteczki telu O
2
określoną związkiem:
V
w
= 4[
3
4
(
2
d
)
3
]
Porónując prawe strony powyższych dwóch zależności
A
N
b
=
3
16
(
2
d
)
3
otrzymano promień cząsteczki telnu O
2
, przy założeniu, że ma ona kształt kulisty
r =
2
d
=
3
16
3
A
N
b
5. Rachunek mian:
[r] =
3
3
mol
mol
m
= m
6. Obliczenie wartości promienia cząsteczki tlenu.
r =
2
d
=
3
16
3
A
N
b
=
3
23
6
10
022
,
6
16
10
25
3
=
9
10
135316
,
0
=
35316
,
1
[Ǻ]
d = 2r =
35316
,
1
2
= 2,70632 [Ǻ] = 0,270632 [nm]
Zadanie 1.15
Wyznaczyć a następnie obliczyć wartość pracy bezwzględnej objętościowej ΔL wykonanej
przez układ nad otoczeniem w przemianie izotermicznej odwracalnej rozgęszczenia gazu
rzeczywistego o zasobie ilości materii n=1[kmol] od początkowego zasobu objętości
V
1
=10[dm
3
] do końcowego zasobu objętości V
2
=2V
1
w temperaturze T=293,15[K] dla gazu
rzeczywistego van der Waalsa spełniającego poniższe równanie.
+
.
. ( − . ) = . .
Gazem rozgęszczanym jest azot dla którego stałe w równaniu stanu van der Waalsa mają
wartości
a
n
=0,1408[
] b=3.91[
]=3,91 10
-3
[
]
Uniwersalna stała gazowa B=8314,3[
]
Rozwiązanie:
Dane:
Wyznaczyć a następnie obliczyć wartość pracy
V
1
=10[dm
3
]
bezwzględnej objętościowej:
V
2
=2 V
1
ΔL
T=293,15[K]=const
n=1[kmol]
B=8314[
]
a
n
=0.1408[
]
b=3.91[
]=3.91 10
-3
[
]
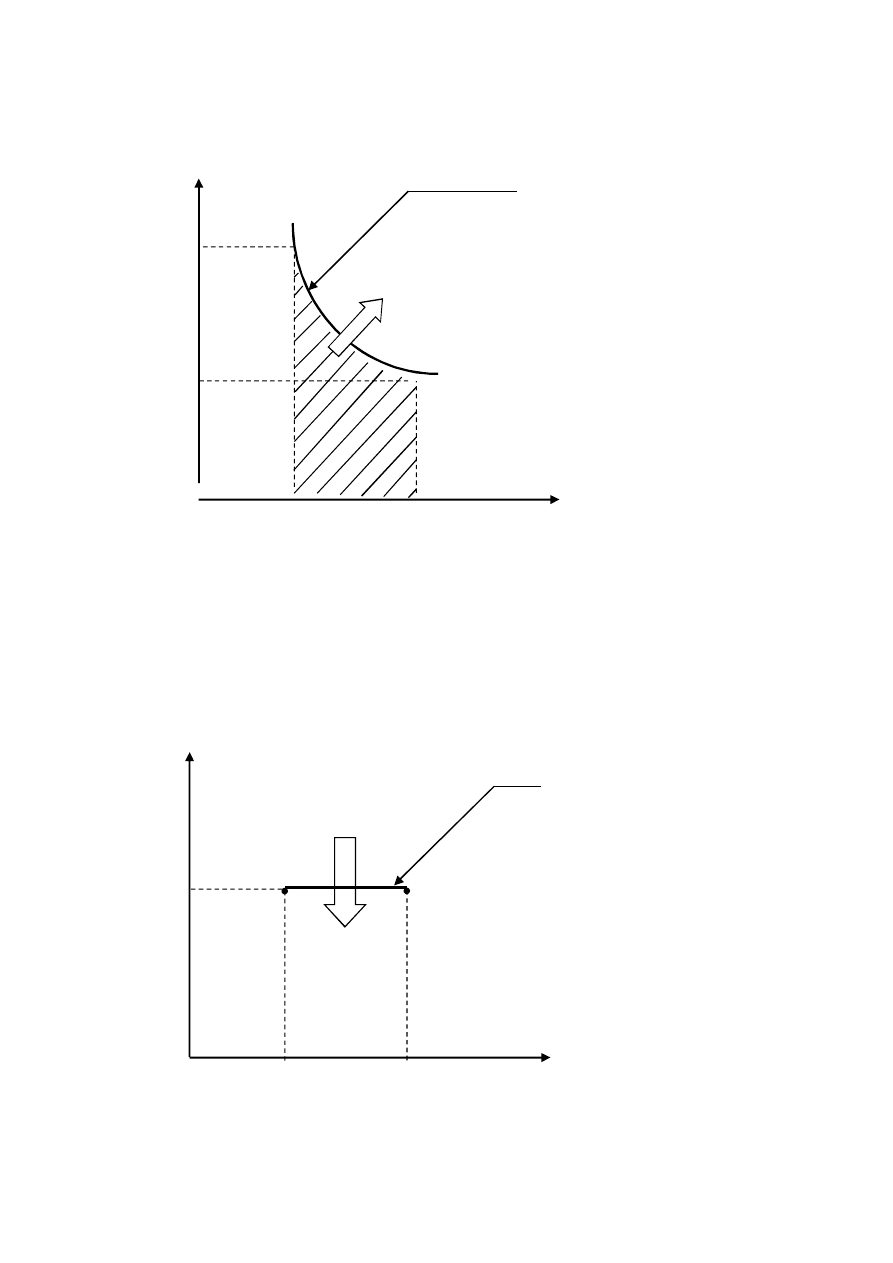
1. Wykresy pracy i ciepła w przemianie izotermicznej w układzie współrzędnych pV i
TS
Ilustracja pracy bezwzględnej objętościowej przemiany izotermicznej gazu rzeczywistego van
der Waalsa we współrzędnych p, V.
Ilustracja ciepła przemiany izotermicznej gazu rzeczywistego van der Waalsa we
współrzędnych T,S.
p(V,T=const)
V
V
1
V
2
p
1
p
2
p
ΔL
1-2
T(S)
T
1-2
T
ΔQ
1-2
S
2
S
1
S
2
1
2. Wyznaczenie pracy bezwzględnej objętościowej.
Z definicji pracy bezwzględnej objętościowej
δL=pdV
oraz z równania stanu gazu rzeczywistego van der Waalsa
p=
(
)
– a
otrzymano
δL=nBT
– n
2
a
Całkując powyższe równanie w granicach
=
−
−
i przyjmując oznaczenie
x=V-nb
obliczono jej różniczkę
dx=v
oraz ustalono nowe granice całkowania
x
1
=V
1
-nb
x
2
=V
2
-nb
Całkowane równanie przekształcono do postaci
1
2
2
1
2
1
V
V
V
a
n
x
dx
nBT
L
n
x
x
Po dokonaniu całkowania
ΔL=nBTln +n
2
a
n
( - )
oraz uwzględnieniu nowych granic całkowania otrzymano wyrażenie określające
pracę bezwzględną objętościową wykonaną w przemianie izotermicznej przez gaz
rzeczywisty van der Waalsa .
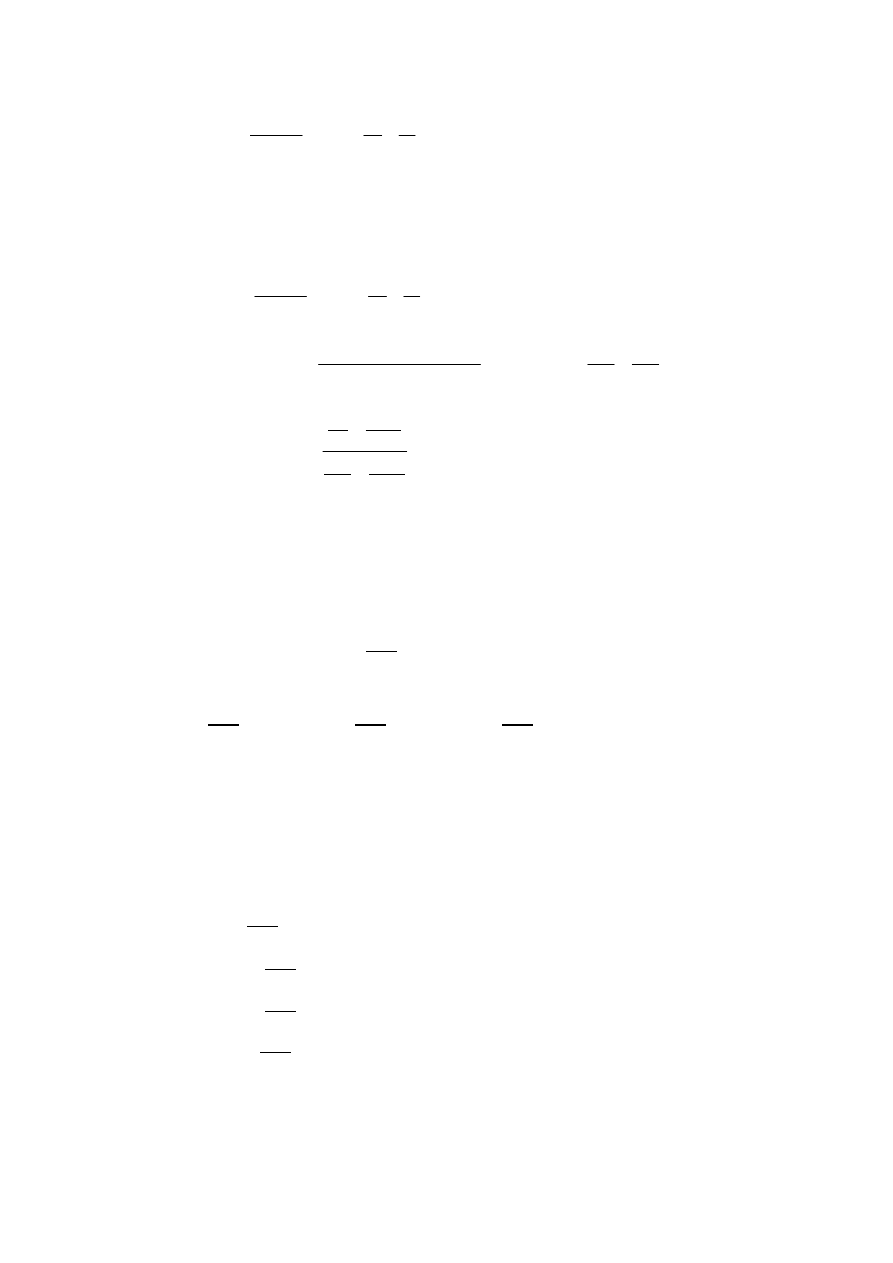
ΔL=nBTln
nb
V
nb
V
1
2
+n
2
a
n
1
2
1
1
V
V
3.Obliczenie wartości pracy bezwzględnej objętościowej
ΔL= nBTln
nb
V
nb
V
1
2
+n
2
a
n
1
2
1
1
V
V
=
=
10
10
20
10
1408
,
0
1
10
91
,
3
1
10
10
10
91
,
3
1
10
20
ln
15
,
293
3
,
8314
1
3
3
2
3
3
3
3
=
=
]
[
10
368
,
2
)
100
50
(
1408
,
0
1000
91
,
3
100
1
1000
91
,
3
50
1
ln
15
,
293
3
,
8314
1
6
J
Zadanie 1.7
Wyznaczyć, a następnie obliczyć wartości zasobów ilości materii [n]=kmol oraz objętości
normalnej obliczeniowej [V
no
]=m
3
odniesionej do normalnych warunków obliczeniowych
(
p =1[bar], t =0[
0
C],
ϑ =22,71[
]) zasobu masy m=100[kg] tlenu (O
2
), azotu (N
2
) i
dwutlenku węgla (CO
2
). Masy cząsteczkowe poszczególnych gazów są następujące:
M =31,999 [
],
M =28,013 [
],
M
=44,01 [
].
Rozwiązanie:
Dane:
Wyznaczyć a następnie obliczyć wartości:
m = m = m
= 100 [kg]
n , n , n
ϑ =22,71 [
]
V
,
V
,
V
M =31,999 [
]
M =28,013 [
]
M
=44,01 [
]
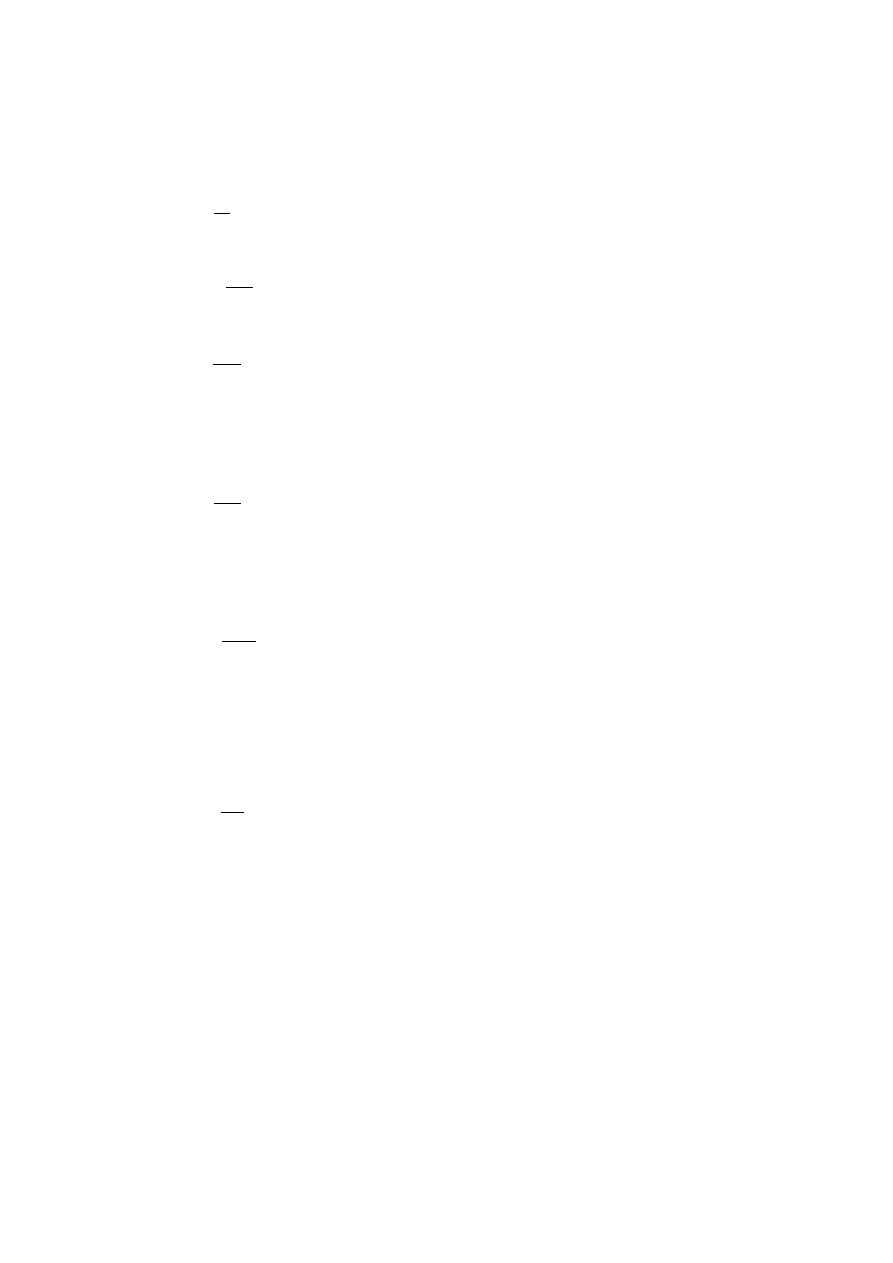
1.Wyznaczenie zasobu ilości materii tlenu, azotu i dwutlenku węgla:
Z definicji masy cząsteczkowej
M =
otrzymano dla tlenu
M
=
zatem zasób ilości materii tlenu cząsteczkowego jest równy
n
=
Analogicznie dla azotu
n
=
oraz dwutlenku węgla
n
=
2.Wyznaczenie zasobu objętości normalnej obliczeniowej tlenu, azotu i dwutlenku węgla:
Z definicji molowej gęstości zasobu objętości gazu w normalnych warunkach obliczeniowych
ϑ
=
określono objętość normalną obliczeniową tlenu
V
= ϑ
∙ n
następnie azotu
V
= ϑ
∙ n
oraz dwutlenku węgla
V
= ϑ
∙ n
3. Rachunek mian dla zasobu ilości materii tlenu, azotu i dwutlenku węgla:
n
= n
= n
=
= kmol
4. Rachunek mian dla zasobu objętości normalnej obliczeniowej tlenu, azotu i dwutlenku
węgla:
V
= V
= V
= kmol ∙
= m
5. Obliczenie wartości zasobu ilości moli tlenu:
n
=
=
,
= 3,1251 [kmol]
6. Obliczenie wartości zasobu ilości moli azotu:
n
=
=
,
= 3,5698 [kmol]
7. Obliczenie wartości zasobu ilości moli dwutlenku węgla:
n
=
=
,
= 2,2722 [kmol]
8. Obliczenie wartości zasobu objętości normalnej obliczeniowej tlenu:
V
= ϑ
∙ n
= 22,71 ∙ 3,1251 = 70,971 [m ]
9. Obliczenie wartości zasobu objętości normalnej obliczeniowej azotu:
V
= ϑ
∙ n
= 22,71 ∙ 3,5698 = 81,07 [m ]
10. Obliczenie wartości zasobu objętości normalnej obliczeniowej dwutlenku węgla:
V
= ϑ
∙ n
= 22,71 ∙ 2,2722 = 51,602 [m ]
Zadanie 1.18
Ciśnienie statyczne przepływającej rurociągiem strugi wody równe jest
0
s
p
[MPa ].
Ciśnienie otoczenia wynosi
1000
0
p
[hPa] , zaś ciśnienie całkowite absolutne
ca
p
przepływającej wody wyrażone w milimetrach słupa rtęci jest równe
ca
h =790 [mmHg].
Obliczyć prędkość substancjalną u przepływającej wody wiedząc , że objętościowa gęstość
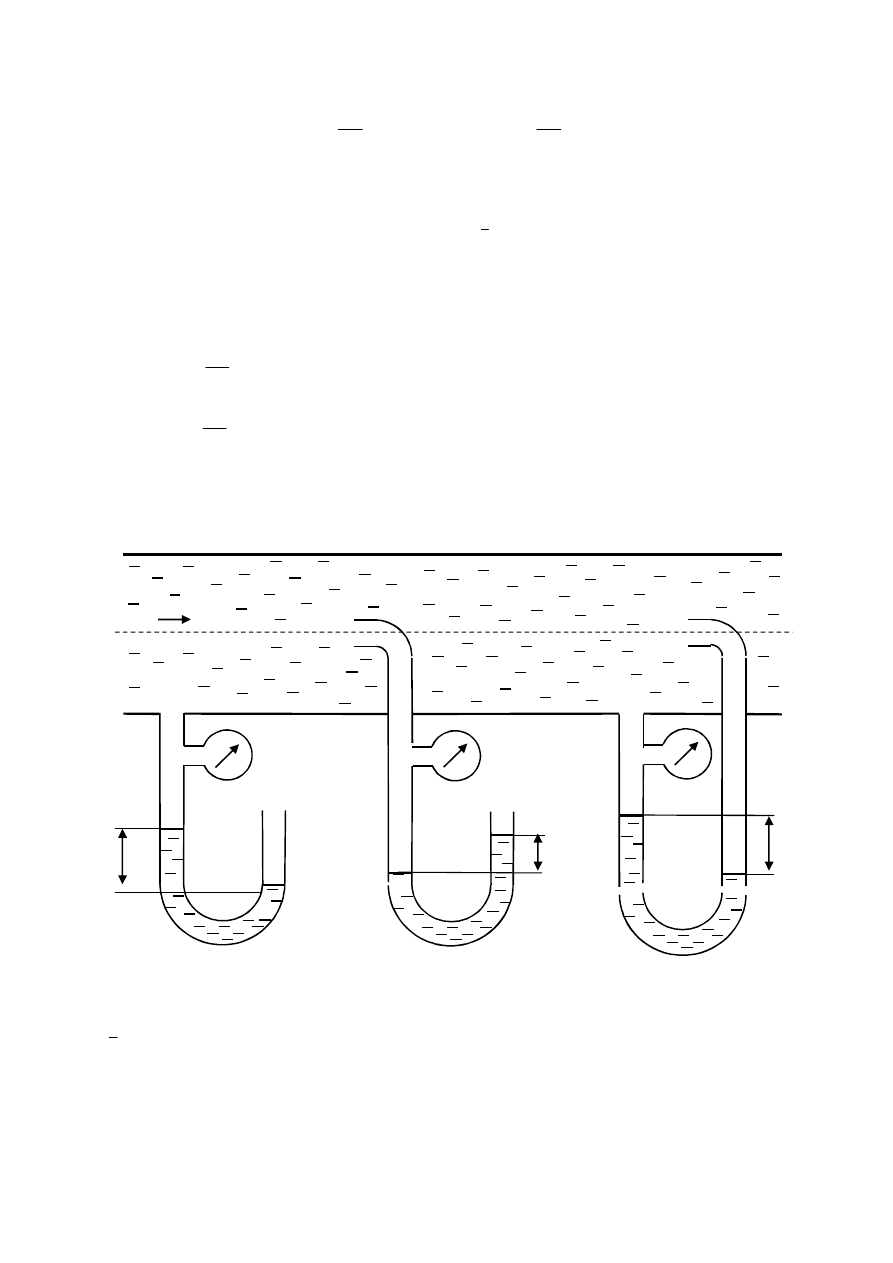
zasobu masy rtęci
]
[
13546
3
m
kg
Hg
zaś wody
]
[
1000
3
0
2
m
kg
H
.
Rozwiązanie
Dane:
Wyznaczyć a następnie obliczyć wartość:
]
[
0 hPa
p
s
u
]
[
1000
0
hPa
p
]
[
790 mmHg
h
ca
3
13546
m
kg
Hg
3
0
1000
2
m
kg
H
1. Ilustracja pomiaru ciśnień w przepływie strugi płynu, płynącego z prędkością
substancjalną:
u prędkość substancjalna wody
0
2
H
objętościowa gęstość zasobu masy wody
c
p
ciśnienie całkowite
p
s
p
sa
p
sa
p
o
u
p
ca
p
ca
p
o
p
c
p
ca
p
d
p
sa
o
p
ciśnienie otoczenia
sa
p
ciśnienie statyczne absolutne
ca
p
ciśnienie całkowite absolutne
d
p
ciśnienie dynamiczne
Zgodnie z ilustracją modelu pomiaru ciśnień w przepływie strugi płynu z prędkością
substancjalną możemy zapisać zależności:
o
c
ca
p
p
p
o
s
sa
p
p
p
s
c
sa
ca
d
p
p
p
p
p
Gdzie ciśnienie dynamiczne jest objętościową gęstością zasobu substancjalnej energii
kinetycznej płynu
2
2
u
p
d
2. Wyznaczenie ciśnienia całkowitego absolutnego p
ca
wyrażonego w jednostkach układu SI.
Odwzorowanie wartości ciśnienia całkowitego absolutnego wyrażonego w milimetrach słupa
rtęci na wartość ciśnienia p
ca
wyrażonego w jednostkach układu SI dokonano przy użyciu
poniższej funkcji
g
h
p
Hg
ca
ca
3. Wyznaczenie ciśnienia dynamicznego
d
p przepływającej wody:
Ciśnienie dynamiczne równe jest różnicy ciśnień absolutnych, całkowitego i statycznego
przepływającej wody:
sa
ca
d
p
p
p
Ciśnienie statyczne absolutne równe jest sumie ciśnień statycznego i otoczenia
o
s
sa
p
p
p
Stąd:
o
s
ca
d
p
p
p
p
Uwzględniając iż:
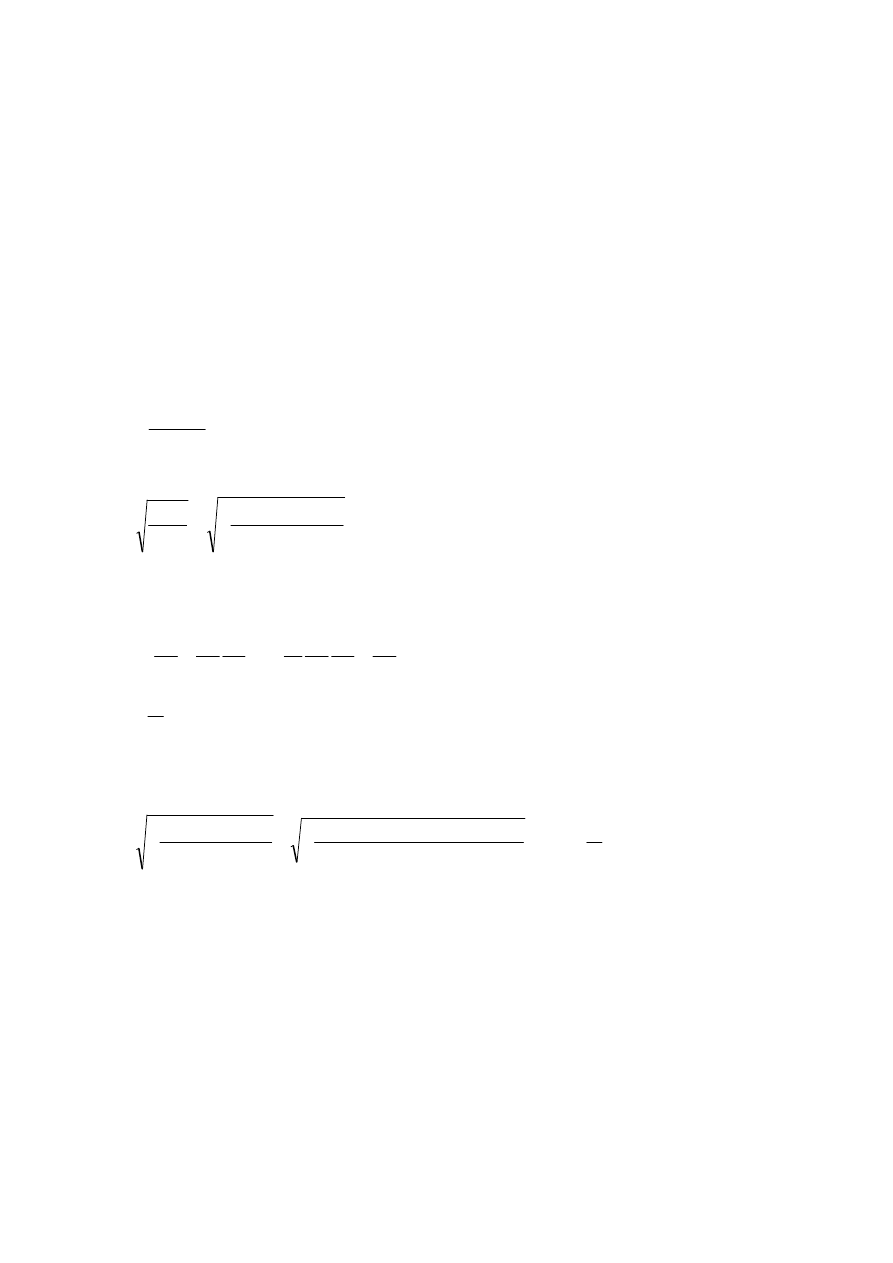
0
s
p
otrzymano:
o
Hg
ca
o
ca
d
p
g
h
p
p
p
4. Wyznaczenie prędkości substancjalnej przepływającej strugi wody.
Uwzględniając definicję ciśnienia dynamicznego w przepływającej strudze wody:
2
2
2
u
p
O
H
d
otrzymano:
O
H
o
Hg
ca
O
H
d
p
g
h
p
u
2
2
)
(
2
2
5. Rachunek mian prędkości substancjalnej przepływającej strugi wody:
2
2
3
2
2
3
2
2
1
]
[
s
m
kg
m
m
s
m
kg
kg
m
m
N
kg
Pa
u
s
m
u
]
[
6.Obliczanie wartości prędkości substancjalnej przepływającej strugi wody:
O
H
o
Hg
ca
p
g
h
u
2
)
(
2
=
]
[
156
,
3
1000
)
100000
81
,
9
13546
79
,
0
(
2
s
m
Zadanie 2.6
Mieszaninę gazów, której skład określony jest udziałami masowymi
5
,
0
2
N
g
;
4
,
0
2
O
g
;
1
,
0
2
O
H
g
przepuszczono przez warstwę absorbującą wodę. Osuszony roztwór wprowadzono
do pustego zbiornika w którym po napełnieniu panuje ciśnienie p=0,4[MPa]. Masy
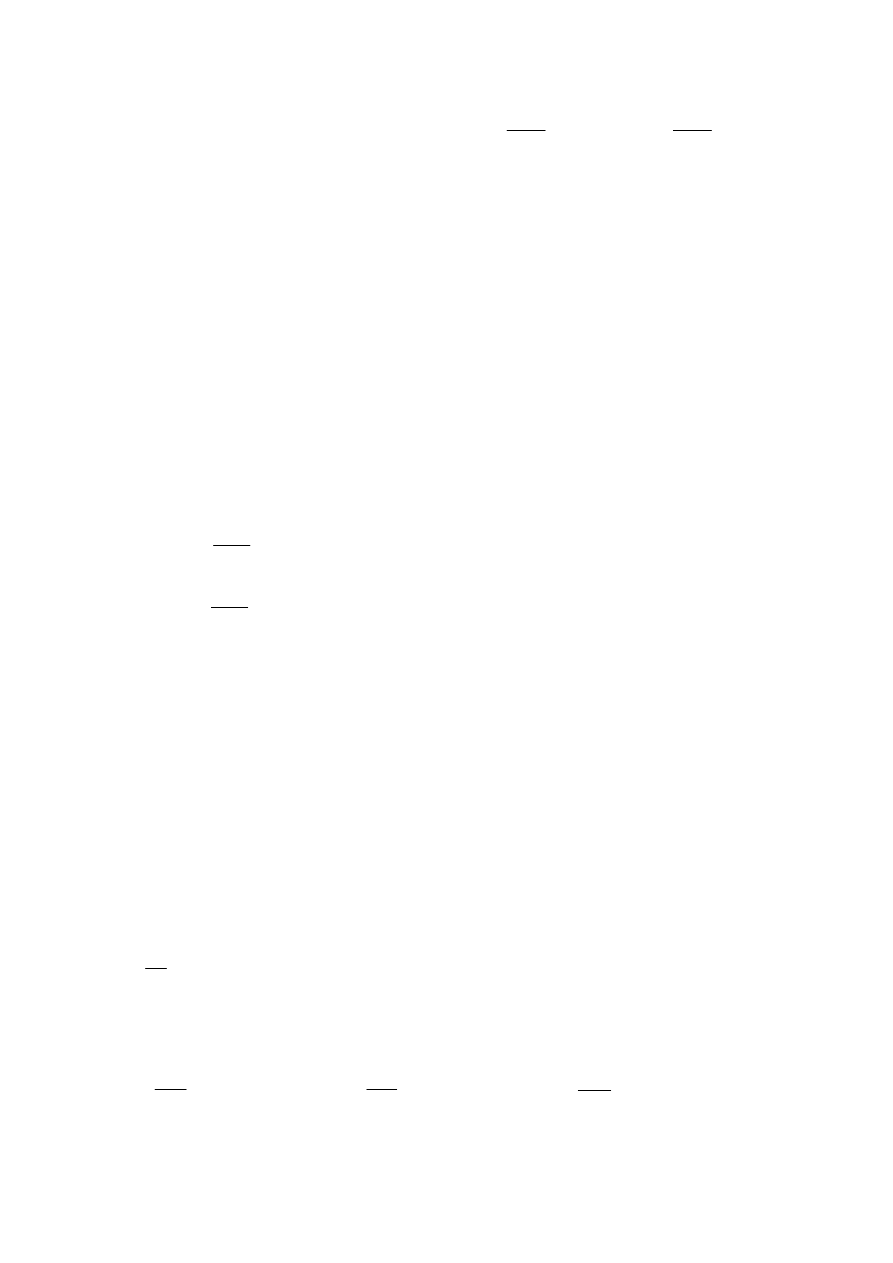
cząsteczkowe azotu i tlenu są następujące M
N
2
=28,016
]
[
kmol
kg
M
O
2
=31,999
]
[
kmol
kg
.
Obliczyć udziały masowe i molowe, masę cząsteczkową oraz ciśnienia składnikowe gazów w
zbiorniku.
Rozwiązanie
Dane: Wyznaczyć a następnie obliczyć wartości:
g
N
2
=0,5
g
SO
2
g
O
2
=0,4
g
SN
2
g
H
2
O
= 0,1
x
SO
2
2
N
M
=28,016
kmol
kg
x
SN
2
2
O
M
=31,999
kmol
kg
p
o
2
p=0,4[MPa].
p
N
2
M
1. Wyznaczenie udziałów masowych składników mieszaniny gazów osuszonych.
Z definicji zasobu masy składników mieszaniny dla gazu przed jego osuszeniem
otrzymano poniższy bilans
O
H
O
N
i
i
m
m
m
m
m
2
2
2
3
1
Udziały masowe mieszaniny gazów przed osuszeniem zgodnie z definicją udziału masowego
m
m
g
i
i
są następujące
m
m
N
2
2
N
g
;
m
m
O
2
2
O
g
;
m
m
O
H
O
H
2
2
g
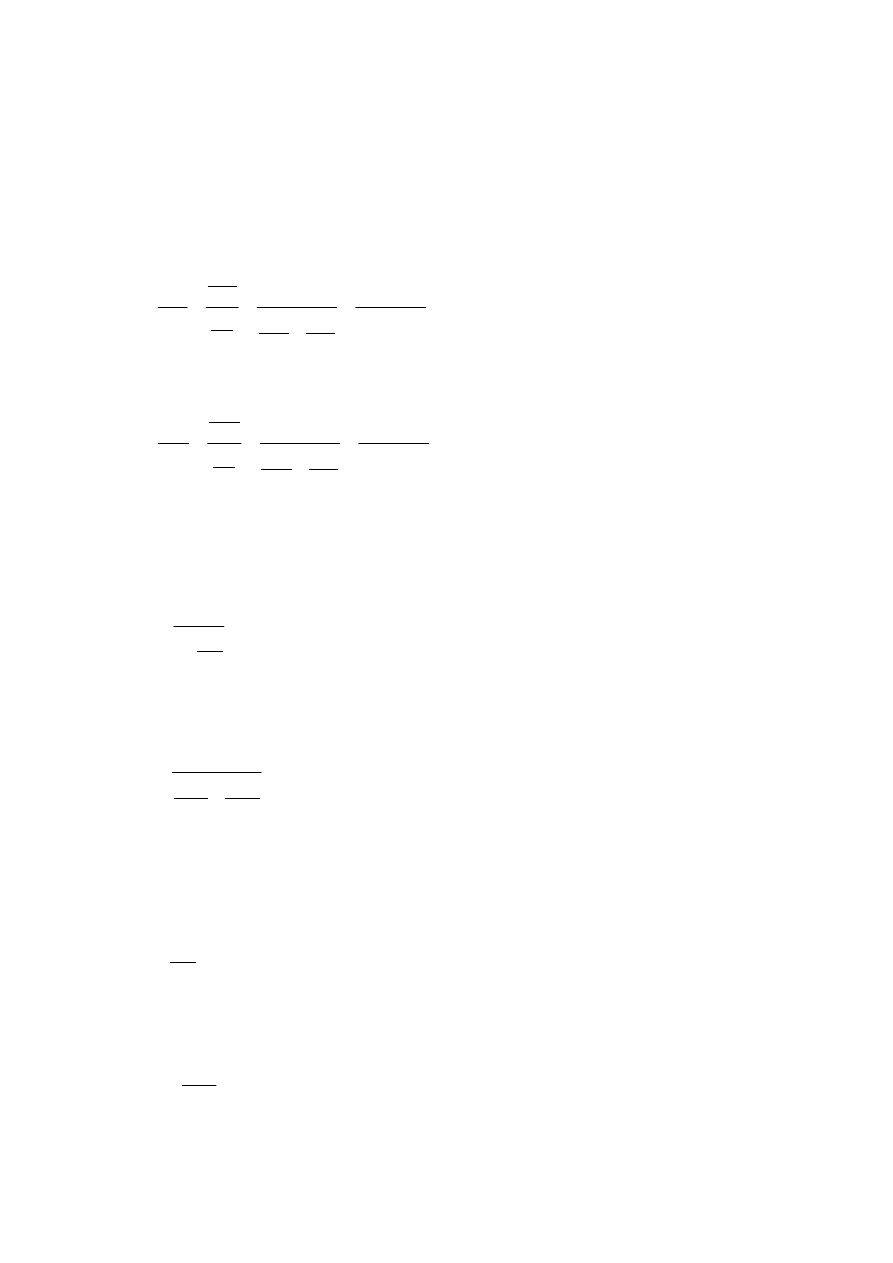
Zasób masy mieszaniny gazów po osuszeniu opisany jest poniższym bilansem
2
2
2
1
O
i
N
si
s
m
m
m
m
Zatem udziały masowe mieszaniny gazów po osuszeniu są odpowiednio równe:
dla tlenu
2
2
2
2
2
2
2
2
2
O
N
O
O
N
O
s
O
s
O
SO
g
g
g
m
m
m
m
g
m
m
m
m
m
m
g
oraz dla azotu
2
2
2
2
2
2
2
2
2
O
N
N
O
N
N
s
N
s
N
SN
g
g
g
m
m
m
m
g
m
m
m
m
m
m
g
2. Wyznaczenie masy cząsteczkowej mieszaniny gazów osuszonych:
Uwzględniając zależność określającą masę cząsteczkową mieszaniny:
2
1
1
i
i
i
M
g
M
otrzymano dla mieszaniny gazów po ich osuszeniu poniższy związek
2
2
2
2
1
N
SN
O
SO
M
g
M
g
M
3. Wyznaczenie udziałów molowych mieszaniny gazów osuszonych:
Uwzględniając zależności określające udziały molowe składnika mieszaniny
i
i
i
g
M
M
x
otrzymano odpowiednio:
dla tlenu
2
2
2
SO
O
SO
g
M
M
x
;
dla azotu
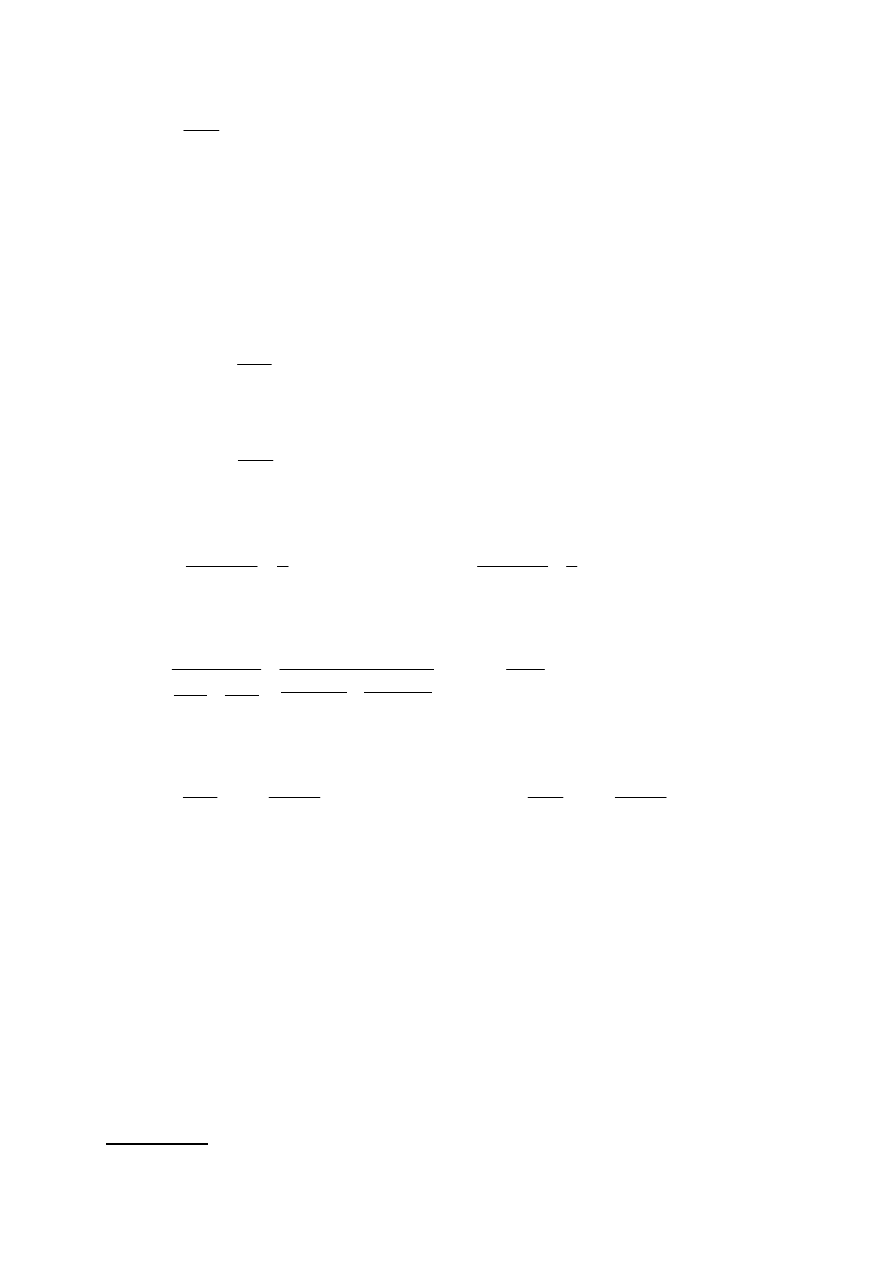
2
2
2
SN
N
SN
g
M
M
x
4. Wyznaczenie ciśnień składników mieszaniny gazów osuszonych:
Uwzględniając zależności określające ciśnienie składników mieszaniny
p
x
p
i
i
otrzymano:
dla tlenu
p
g
M
M
p
x
p
SO
O
SO
O
2
2
2
2
dla azotu
p
g
M
M
p
x
p
SN
N
SN
N
2
2
2
2
5. Obliczanie wartości udziałów masowych składnika mieszaniny gazów osuszonych:
444
,
0
9
4
2
2
2
2
O
N
O
SO
g
g
g
g
555
,
0
9
5
2
2
2
2
O
N
N
SN
g
g
g
g
6. Obliczanie wartości masy cząsteczkowej mieszaniny gazów osuszonych:
]
[
675
,
29
016
,
28
9
5
999
,
31
9
4
1
1
2
2
2
2
kmol
kg
M
g
M
g
M
N
SN
O
SO
7. Obliczanie wartości udziałów molowych składników mieszaniny gazów osuszonych:
412
,
0
444
,
0
999
,
31
675
,
29
2
2
2
SO
O
SO
g
M
M
x
588
,
0
555
,
0
016
,
28
675
,
29
2
2
2
SN
N
SN
g
M
M
x
8.Obliczanie wartości ciśnień składników mieszaniny gazów osuszonych:
]
[
1648
,
0
4
,
0
412
,
0
2
2
MPa
p
x
p
SO
O
]
[
2352
,
0
4
,
0
588
,
0
2
2
MPa
p
x
p
SN
N
Zadanie 2.8
Wyrażenie Pfaffa ma postać
DX = xdy + 2ydx
Znaleźć czynnik całkujący wyrażenie Pfaffa.
Rozwiązanie
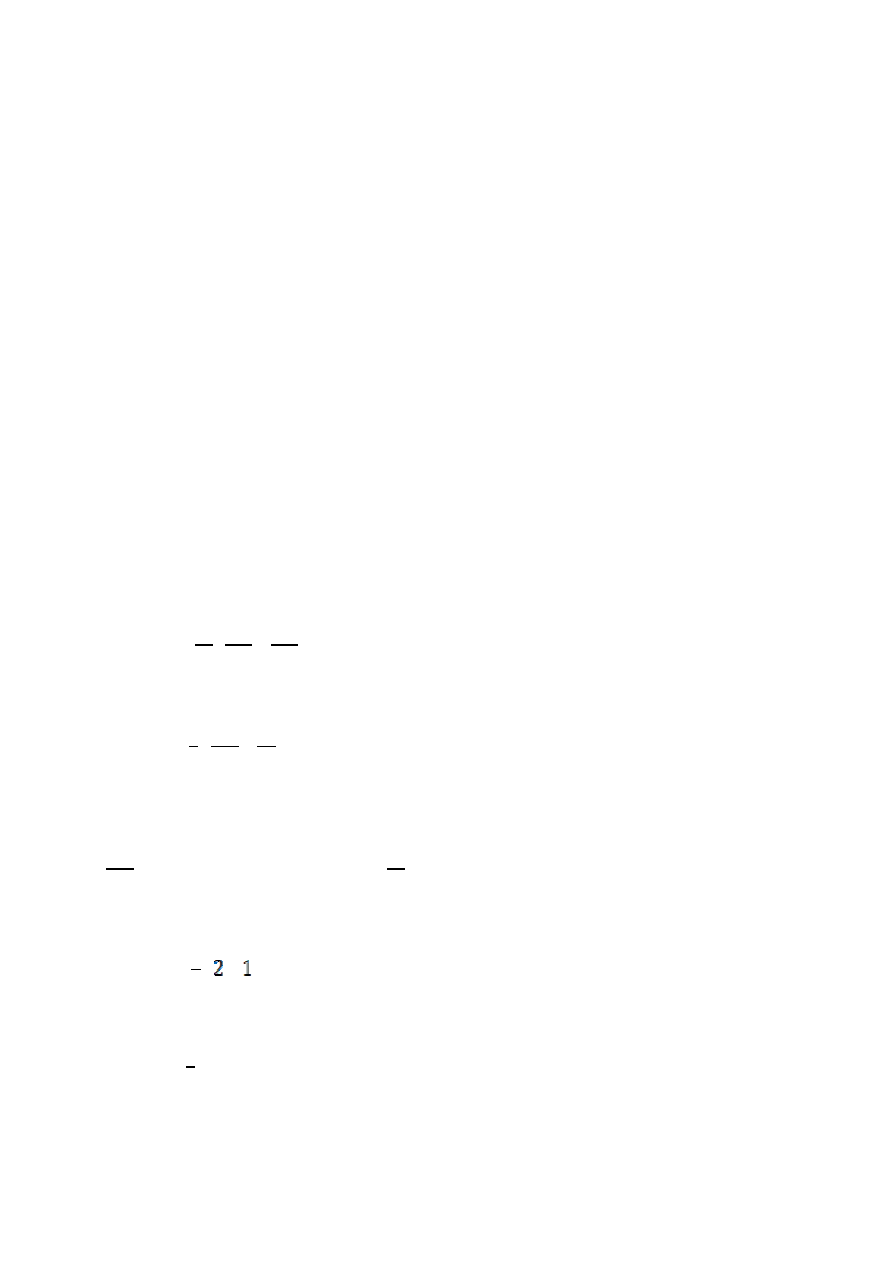
1. Wyznaczenie czynnika całkującego wyrażenia Pfaffa.
Funkcja pierwsza jest równa
X
1
(x
1
,x
2
) = 2y
i odpowiednio zmienna niezależna pierwsza i jej przyrost
x
1
= x dx
1
= dx
Funkcja druga jest równa
X
2
(x
1
,x
2
) = x
i odpowiednio zmienna niezależna druga i jej przyrost
x
2
= y dx
2
= dy
Założono, że czynnik całkujący jest funkcją tylko zmiennej niezależnej pierwszej
(x
1
) = (x)
Mamy zatem
dln(x
1
)
= (
-
)
dx
1
stąd
dln(x)
= (
- )
dx
wykonując różniczkowanie
= 2
oraz
= 1
otrzymano
dln(x) =
( - )
dx
zatem
dln(x) =
dx
lub
dln(x) = dlnx
Całkując powyższe równanie ze stałą całkowania
∫
dln λ( x )=
∫
dlnx + lnc
otrzymano
ln(x) = lnx + lnc
lub
ln(x) = ln(xc)
Zatem czynnik całkujący równy jest
(x) = xc
2. Sprawdzenie poprawności rozwiązania.
Mnożąc wyrażenie Pfaffa przez wyznaczony czynnik całkujący otrzymano
różniczkę zupełną.
(x)DX = cx
2
dy + 2cyxdx
dla której pochodne mieszane muszą być sobie równe.
Pochodne mieszane mają postać
(
)
=
(
)
Po obliczeniu ich wartości
2cx = 2cx
stwierdzono ich równość, co dowodzi, że czynnik całkujący został obliczony
prawidłowo.
Zadanie 3.10
Powietrze traktowane tak jak gaz doskonały o zasobie masy m = 3[kg] rozgęszczono w
przemianie izotermicznej odwracalnej zwiększając jego zasób objętości trzykrotnie. Ciśnienie
i temperatura początkowa powietrza są równe p
1
= 10[at] i t
1
= 300[C]. Indywidualna stała
gazowa powietrza ma wartość R = 287,04 [
kgK
J
]. Wyznaczyć a następnie obliczyć wartość
przyrostu ilości ciepła doprowadzonego do układu oraz pracę bezwzględną objętościową i
techniczną rozgęszczania gazu.
Rozwiązanie
Dane: Wyznaczyć a następnie obliczyć wartości:
m = 3[kg] ∆Q
T = const. L
p
1
= 10[at] L
t
t
1
= 300[
o
C]
R = 287,04
kgK
J
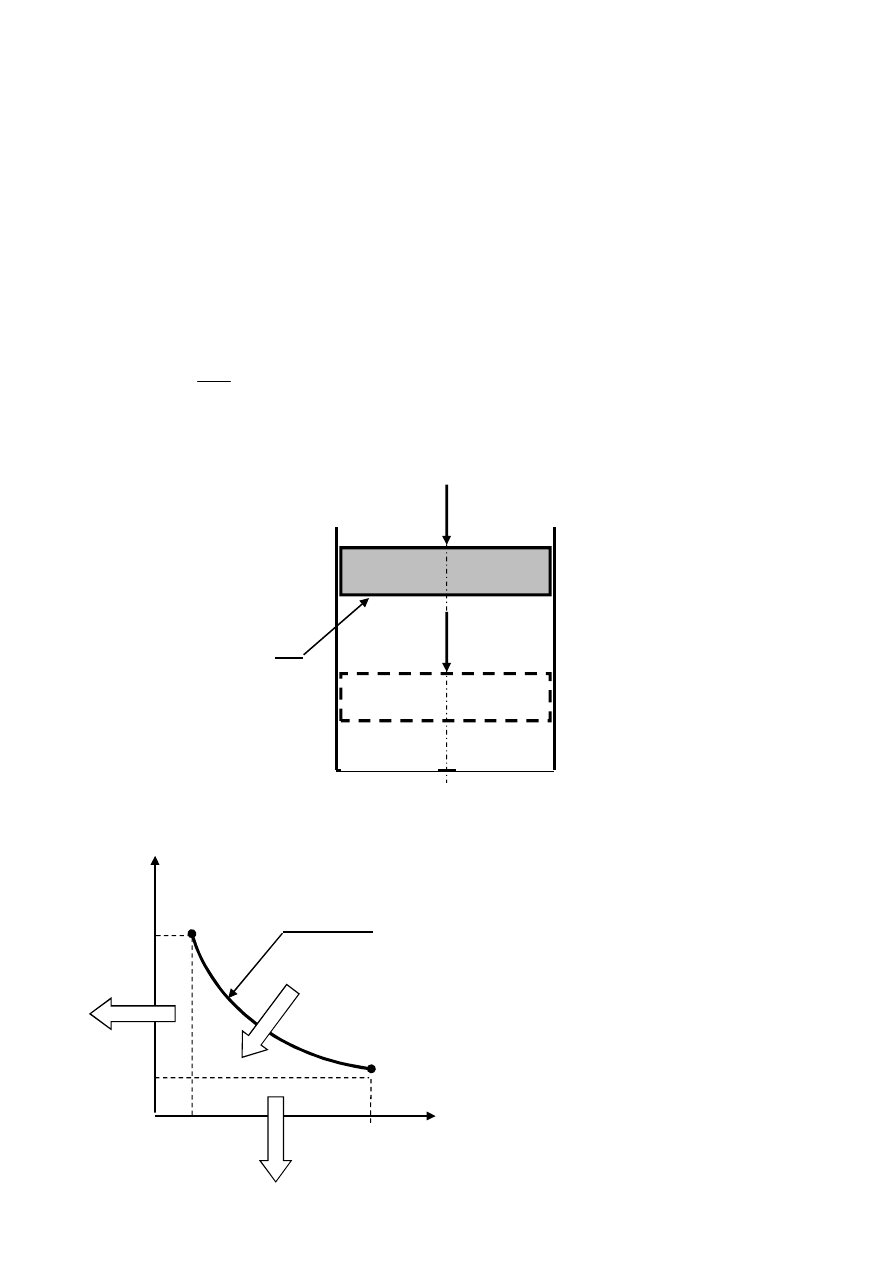
1. Ilustracja układu oraz wykresy przemiany izotermicznej we współrzędnych p, V oraz T, S.
Ilustracja układu cylinder-tłok.
A
F
s2
p
0
V
1
, T=const
F
s1
p
2
= p
s2
+ p
0
p
1
= p
s1
+ p
0
V
2
T=const
p(V, T=const)
p
1
V
p
2
V
1
V
2
L
p
ΔQ
L
t
L
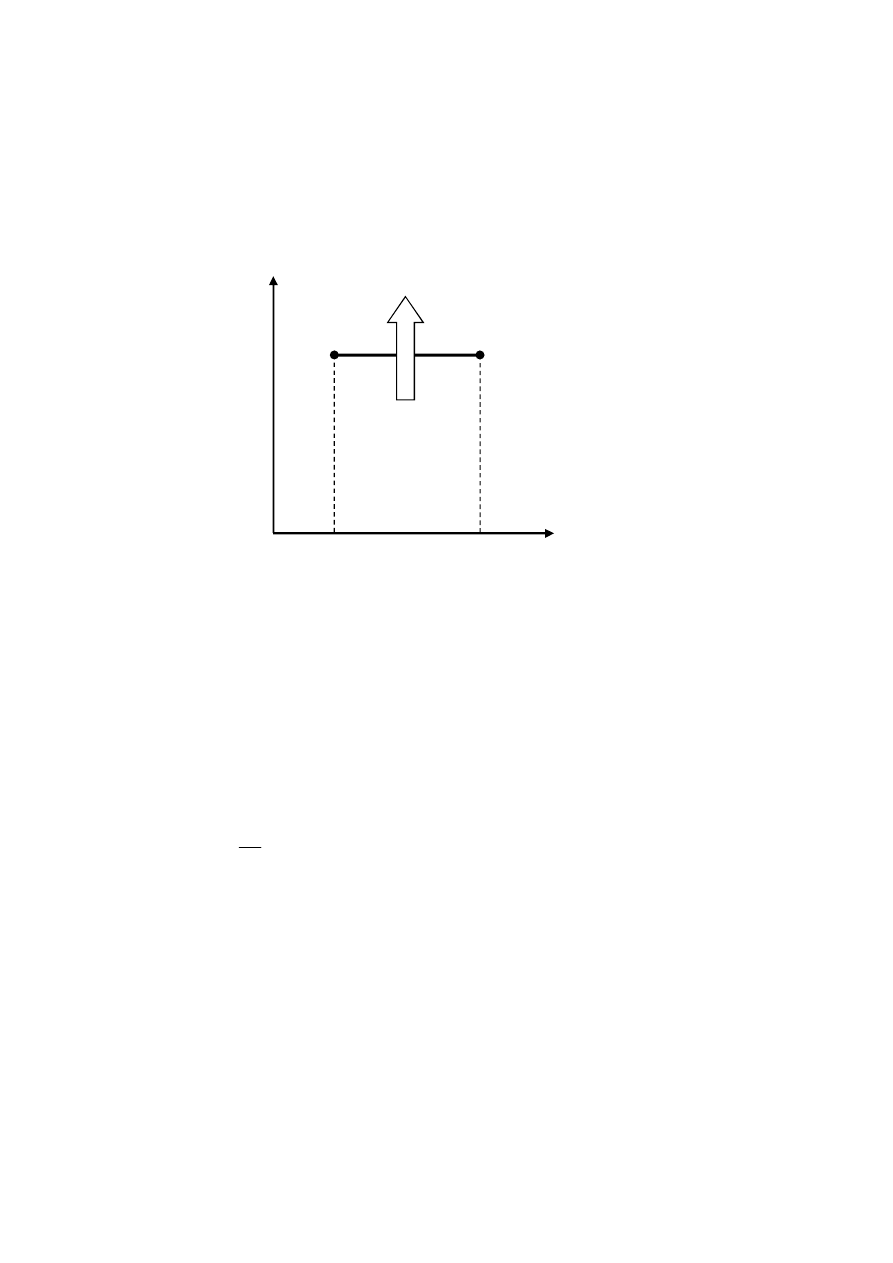
Ilustracja prac bezwzględnej objętościowej L oraz technicznej L
t
przemiany izotermicznej
rozgęszczania powietrza we współrzędnych p, V.
Ilustracja przyrostu ilości ciepła przemiany izotermicznej rozgęszczania powietrza we
współrzędnych
T, S.
1.1 Wyznaczenie ciśnienia statycznego absolutnego.
Ciśnienie statyczne powietrza w układzie pomierzone manometrem:
A
F
p
S
S
Ciśnienie statyczne absolutne powietrza w układzie:
0
p
p
p
p
s
sa
gdzie p
0
jest ciśnieniem otoczenia.
2. Bilans zasobu energii wewnętrznej dla przemiany odwracalnej.
Pierwsza postać pierwszej zasady termodynamiki określona jest zależnością:
L
Q
dE
1
gdzie praca bezwzględna objętościowa jest równa:
pdV
L
S
1
V
S
2
ΔQ
T
T(S)= const
3. Bilans zasobu entalpii dla przemiany odwracalnej.
Druga postać pierwszej zasady termodynamiki określona jest zależnością:
t
L
Q
dH
gdzie praca techniczna jest równa:
Vdp
L
t
4. Bilans zasobu energii wewnętrznej dla przemiany izotermicznej.
Zasób energii wewnętrznej gazu doskonałego w układzie substancjalnym określony jest
związkiem:
mT
c
E
1
gdzie:
Dla gazu doskonałego
.
const
c
Dla układu substancjalnego
.
const
m
Dla przemiany izotermicznej
.
const
T
Zatem elementarny przyrost zasobu energii wewnętrznej będzie równy:
0
1
dE
i bilans zasobu energii wewnętrznej dla przemiany odwracalnej zredukuje się do postaci:
L
Q
5. Bilans zasobu entalpii dla przemiany izotermicznej.
Zasób entalpii gazu doskonałego w układzie substancjalnym określony jest zależnością:
mT
c
H
p
Dla gazu doskonałego
.
const
c
p
Dla układu substancjalnego
.
const
m
Dla przemiany izotermicznej
.
const
T
Zatem elementarny przyrost zasobu entalpii będzie równy
0
dH
i druga postać pierwszej zasady termodynamiki zredukuje się do postaci:
t
L
dQ
6. Wyznaczenie pracy bezwzględnej objętościowej w przemianie izotermicznej.
Uwzględniając definicję pracy bezwzględnej objętościowej
pdV
L
oraz równanie izotermy
.
1
1
const
V
p
pV
z którego wyznaczono ciśnienie gazu w funkcji zasobu jego objętości
V
V
p
p
1
1
1
otrzymano:
V
dV
V
p
L
1
1
Całkując powyższe równanie w granicach
L
V
V
V
dV
V
p
L
0
1
1
1
2
wyznaczono pracę bezwzględną objętościową:
3
ln
ln
ln
ln
1
1
2
1
1
2
1
1
2
1
1
1
mRT
V
V
mRT
V
V
V
p
V
V
V
V
p
L
Z powyższych równań wynika, że dla przemiany izotermicznej przyrost ilości ciepła
przemiany równy jest ilości pracy bezwzględnej objętościowej i pracy technicznej
przemiany
t
L
L
Q
7. Wyznaczenie pracy technicznej i przyrostu ilości ciepła w przemianie izotermicznej
odwracalnej:
3
ln
ln
1
1
2
1
mRT
V
V
mRT
L
L
Q
t
8. Rachunek mian dla pracy bezwzględnej objętościowej, technicznej i przyrostu ilości ciepła.
J
K
kgK
J
kg
Q
L
L
t
]
[
]
[
]
[
9. Obliczenie wartości pracy bezwzględnej objętościowej, technicznej i przyrostu ilości ciepła
rozgęszczonego powietrza w przemianie izotermicznej odwracalnej.
]
[
54223
0986
,
1
15
,
573
04
,
287
3
3
ln
1
J
mRT
L
L
Q
t
Zadanie 3.12
Powietrze traktowane tak jak gaz doskonały o zasobie masy m=1,5[kg] zostało zgęszczone w
przemianie politropowej od wartości początkowych parametrów stanu p
p
=0,09[MPa] i
t
p
=18[
o
C] do wartości końcowych p
k
=1[MPa] i t
k
=125[
o
C].
Wyznaczyć, a następnie obliczyć wartość wykładnika politropy n, pracę bezwzględną
objętościową L oraz przyrost ilości ciepła przemiany ΔQ, wiedząc iż indywidualna stała
gazowa powietrza R=287,04
[
] zaś wykładnik izentropy k=1,4.
Rozwiązanie
Dane:
Wyznaczyć a następnie obliczyć
m=1,5[kg]
wartości:
p
p
=0,09[MPa]
n
t
p
=18[
o
C]
L
p
k
=1[MPa]
ΔQ
T
k
=125[
o
C]
R=287,04[
]
k=1,4
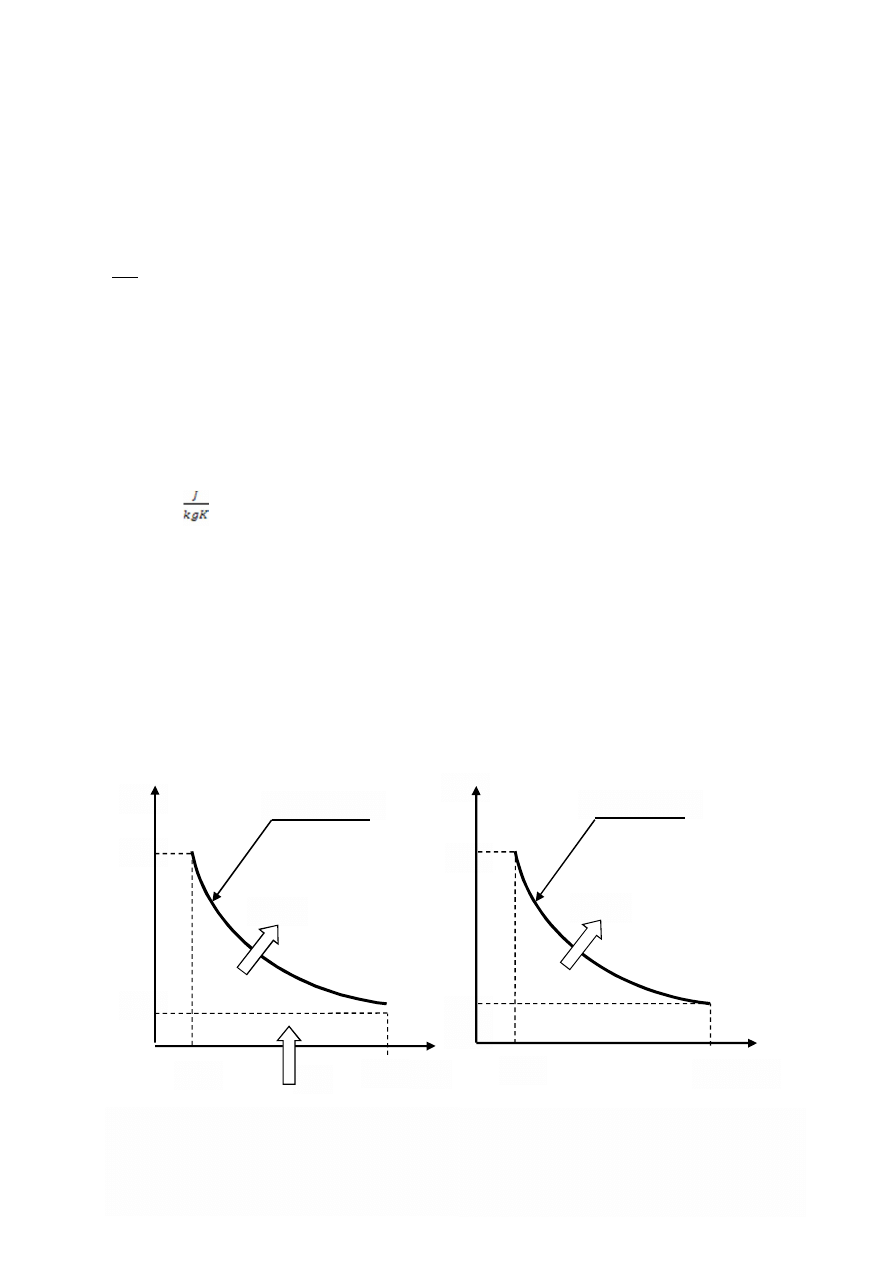
1. Wykresy przemiany politropowej zgęszczenia powietrza we współrzędnych p,V oraz
T,S.
p(V, T
k
=const)
T
k
p
S
k
S
V
T
S
p
T
p
V
k
V
p
Ilustracja pracy bezwzględnej objętościowej
przemiany politropow we współrzędnych p, V.
Ilustracja przyrostu ilości ciepła przemiany
politropowej we współrzędnych T, S.
L
p(V, T
p
=const)
p
k
p
p
ΔQ
ΔQ
2. Podstawowe związki określające politropę.
Z definicji ciepło właściwe politropy jest równe
=
Ciepło właściwe politropy w funkcji ciepła właściwego przy stałej objętości, wykładnika
izentropy oraz wykładnika politropy określone jest zależnością:
=
gdzie wykładnik politropy jest równy
c
c
c
c
n
p
zaś równanie politropy opisane jest związkiem
=
3. Wyznaczanie zasobu objętości powietrza przed i po jego zgęszczeniu.
Z równania stanu gazu doskonałego Clapeyrona wyznaczono:
początkowy zasób objętości powietrza
=
oraz końcowy zasób objętości powietrza
=
4. Wyznaczanie wykładnika politropy.
Z równania politropy dla stanu początkowego i końcowego, uzyskano związek
∙
=
∙
Podstawiając za V
p
oraz V
k
wielkości określone w punkcie 3
∙ (
) =
∙ (
)
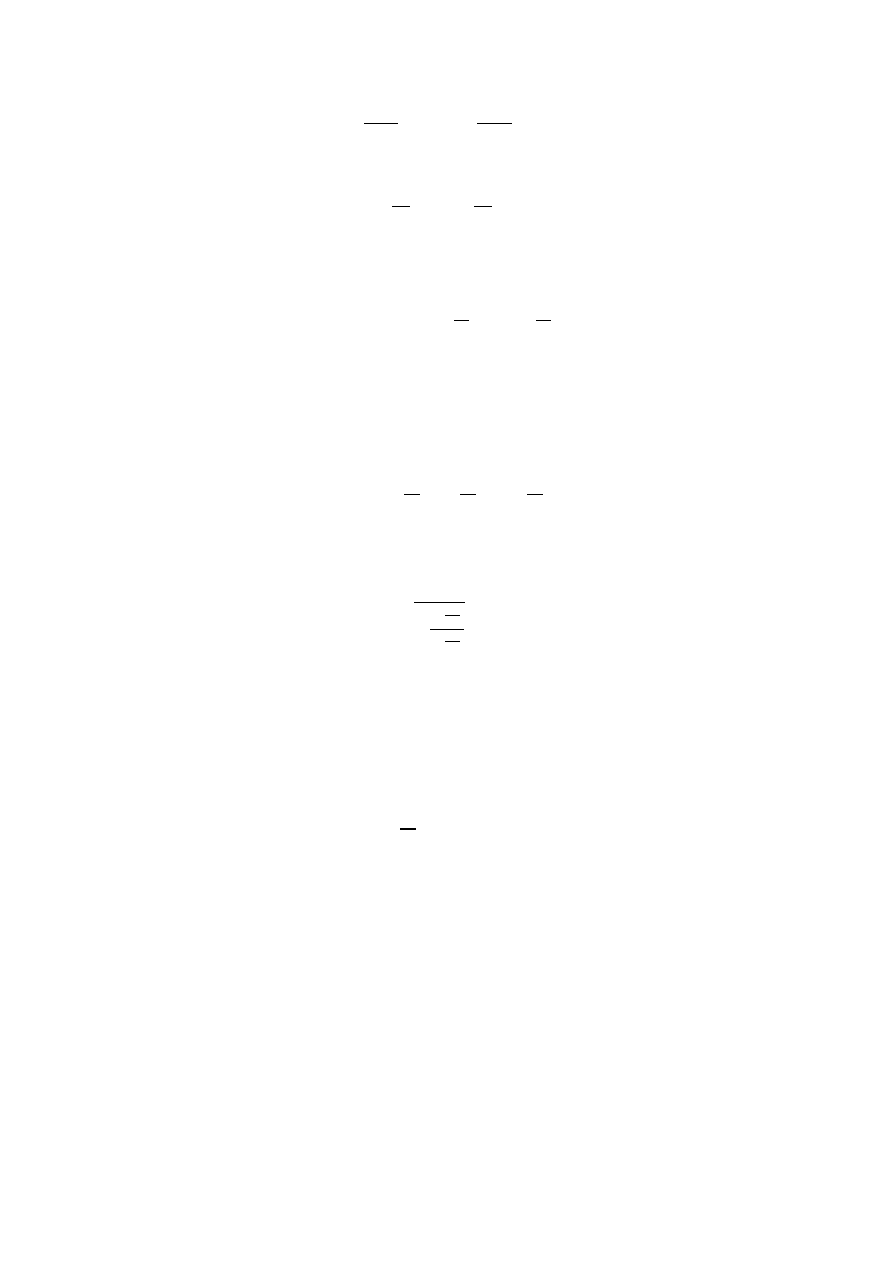
otrzymano
(
)
= ( )
Logarytmując powyższe wyrażenie
(
1 − ) ln
=
( )
a następnie przekształcając je do postaci
+
=
wyznaczono wykładnik politropy
=
(
)
(
)
5. Wyznaczanie przyrostu ilości ciepła przemiany politropowej.
Z definicji ciepła właściwego przemiany politropowej
=
po rozdzieleniu zmiennych i pomnożeniu obustronnie przez zasób masy powietrza
znajdującego się w układzie, otrzymano
=
Ponieważ elementarny przyrost ilości ciepła jest równy
=
zatem
=
Uwzględniając ciepło właściwe politropy określone związkiem
=
∙
równanie Meyera
=
−
oraz definicję wykładnika izentropy
=
otrzymano w pierwszej kolejności zależność określającą ciepło właściwe przy stałej objętości
=
a następnie ciepło właściwe politropy
=
(
)
∙
(
)
(
)
Zatem przyrost ilości ciepła w przemianie politropowej określony jest związkiem
=
( − 1)
∙
( − )
( − 1)
∙
Całkując powyższe równanie w granicach
∫
=
(
)
(
)(
)
∆
∙
∙ ∫
otrzymano przyrost ilości ciepła w przemianie politropowej.
∆ =
∙
∙
∙ (
−
)
6. Wyznaczanie pracy bezwzględnej objętościowej przemiany politropowej.
Z równania politropy
=
=
określono ciśnienie w funkcji zasobu objętości
=
∙
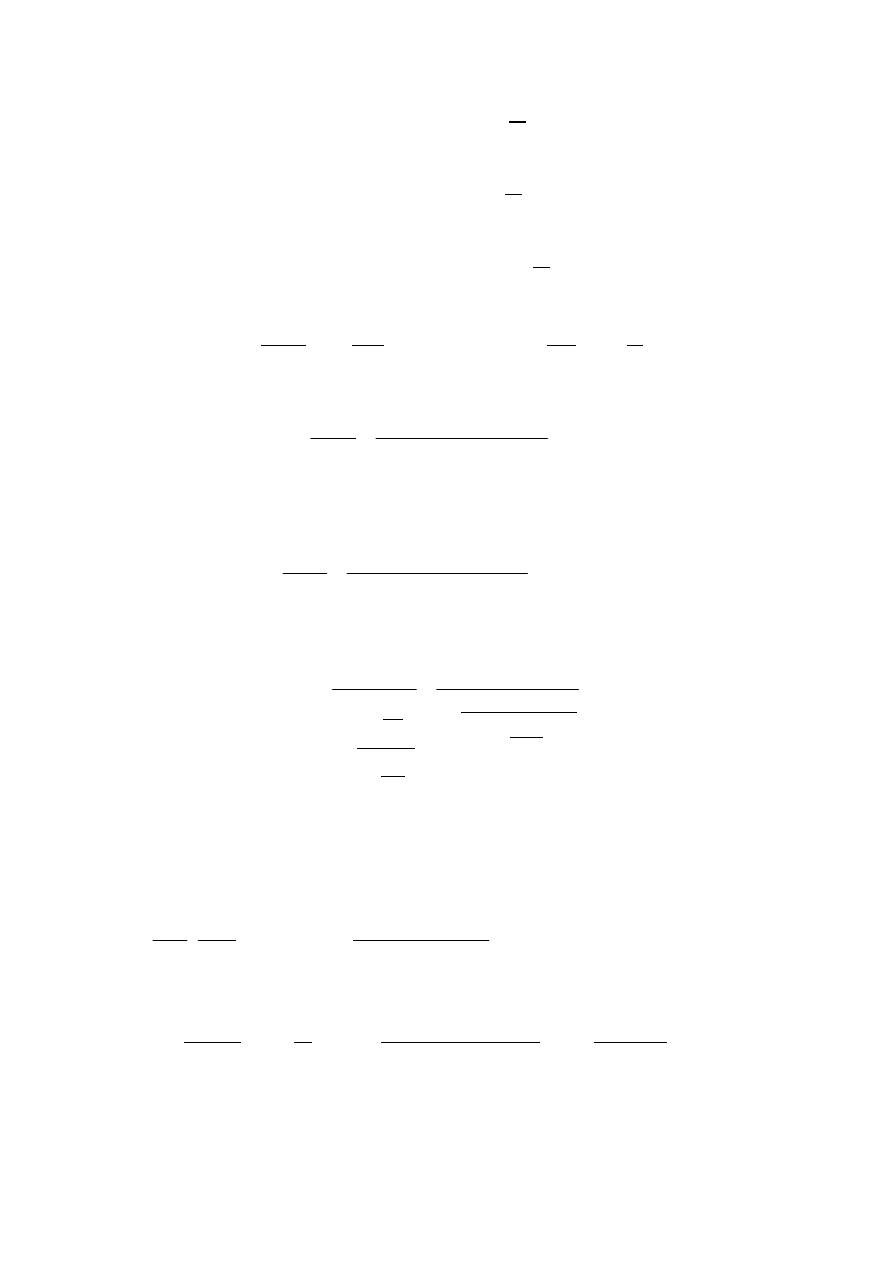
Uwzględniając definicję pracy bezwzględnej objętościowej i ostatni związek, otrzymano
=
Całkując powyższe równanie w granicach
∫
=
∫
uzyskano wyrażenie określające pracę bezwzględną objętościową przemiany politropowej
=
∙
[
(
)
]
=
(
)
−
(
)
=
1 − ( )
(
)
7. Obliczenie wartości zasobu objętości powietrza przed zgęszczeniem.
39291
,
1
10
09
,
0
)
15
,
273
18
(
04
,
287
5
,
1
6
p
p
p
p
mRT
V
8. Obliczenie wartość zasobów objętości powietrza po zgęszczeniu.
3
6
171432
,
0
10
09
,
0
)
15
,
273
125
(
04
,
287
5
,
1
m
p
mRT
V
k
k
k
9. Obliczenie wartości wykładnika politropy.
1494
,
1
1
09
,
6
ln
15
,
273
125
ln
1
1
ln
ln
1
1
k
p
p
k
p
p
T
T
n
10. Obliczenie wartość przyrostu ilości ciepła w przemianie politropowej.
kJ
T
T
m
n
k
n
k
R
Q
p
k
191
,
193
)
15
,
291
15
,
398
(
5
,
1
)
1
1494
,
1
)(
1
4
,
1
(
)
4
,
1
194
,
1
(
04
,
287
)
(
1
1
11. Obliczenie wartość pracy bezwzględnej objętościowej, przemiany politropowej.
=
( − 1)
1 −
=
0,09 ∙ 10 + 1,39291
1,1494 − 1
1 −
1,39291
0,171432
,
= −308,37[ ]