
Kolokwium 1
1. Policzyã pochodne funkcji : a)
x
arctgx
x
e
y
x
3
4
3
2
,
b)
1
4
4
3
ln
cos
x
x
x
y
, c)
x
x
ctgx
y
4
arcsin
1
2
, d)
3
4
5
4
3
1
5
x
x
x
y
, e)
15
sin
2
x
x
y
.
2. Wyznaczyã dziedzinê funkcji:
x
f
x
x
x
x
f
x
1
3
log
2
1
3. Wyznaczyã asymptoty, ekstrema i przedziaùy monotonicznoœci dla
2
2
7
)
(
2
x
x
x
x
f
.
4. Wyznaczyã równanie stycznej do krzywej
1
3
2
x
x
ln
y
dla x = 1.
5. Obliczyã granice: a)
2
0
4
arcsinx
5
lim
x
tgx
x
xe
x
x
, b)
x
x
x
4
3
4
1
lim
.
6 .(grupa 103). Przybli¿yã funkcjê
4
2
x
e
y
sum¹ 3 kolejnych potêg
jednomianu
2
x
.
6. (grupa 104) . Zbadaã ci¹gùoœã funkcji
1
0
1
1
)
1
(
arcsin
2
2
)
(
x
dla
x
dla
x
x
x
f
w punkcie 1 .
id6204203 pdfMachine by Broadgun Software - a great PDF writer! - a great PDF creator! - http://www.pdfmachine.com http://www.broadgun.com

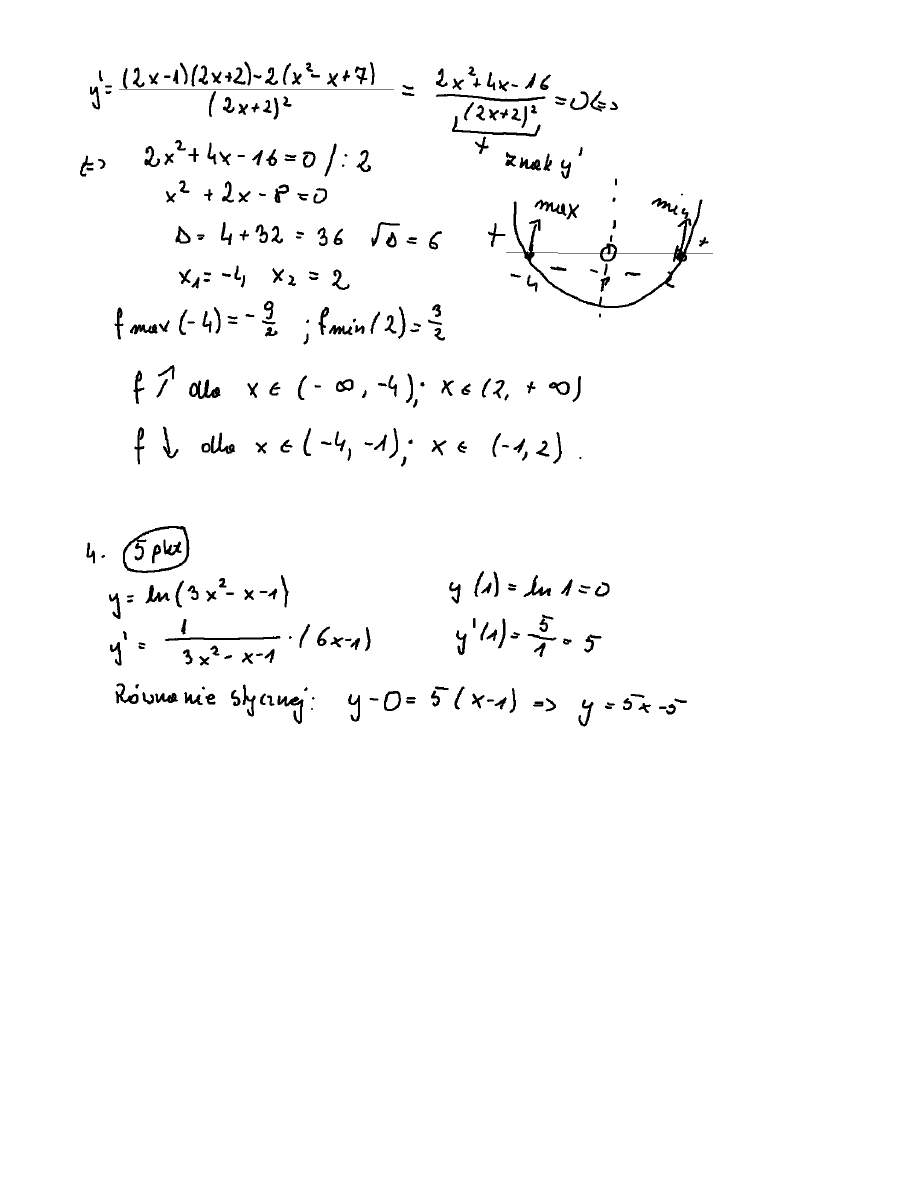
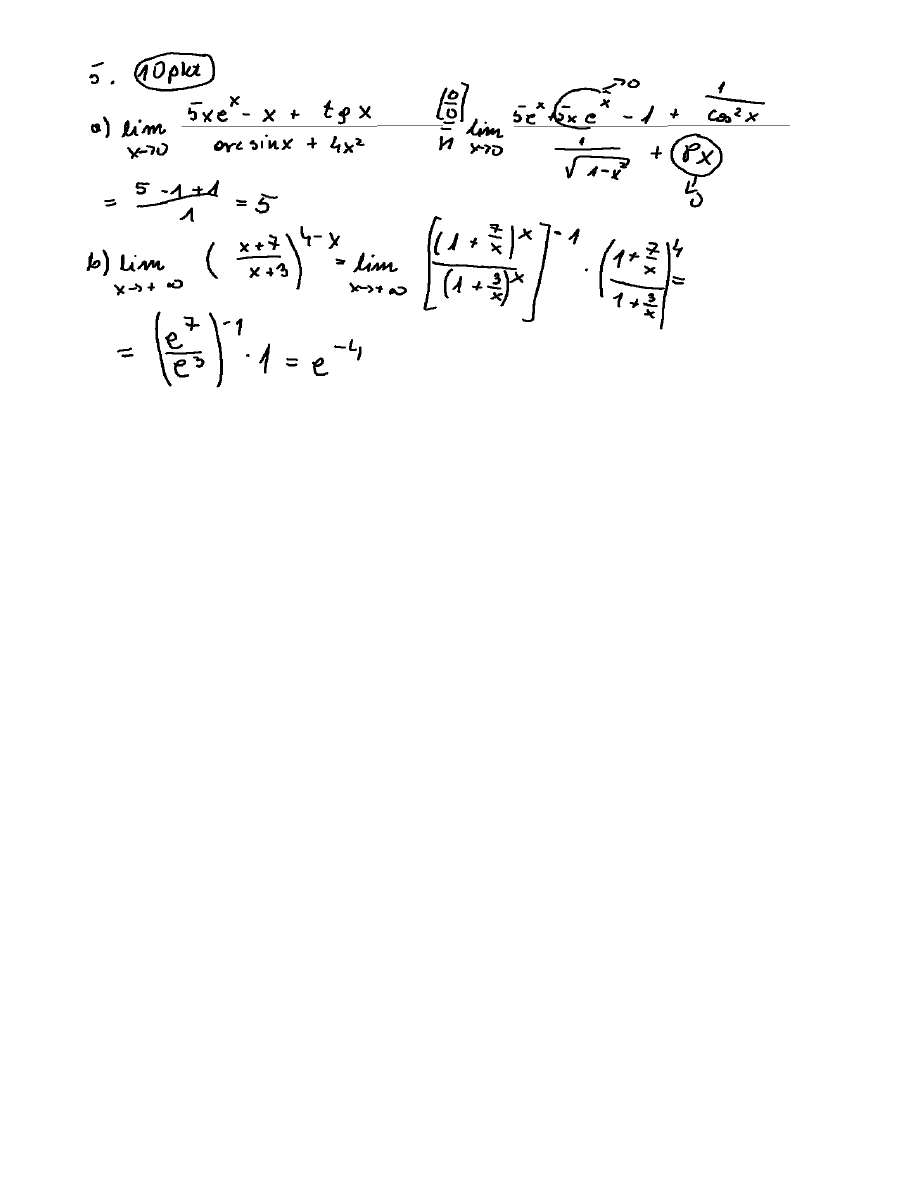
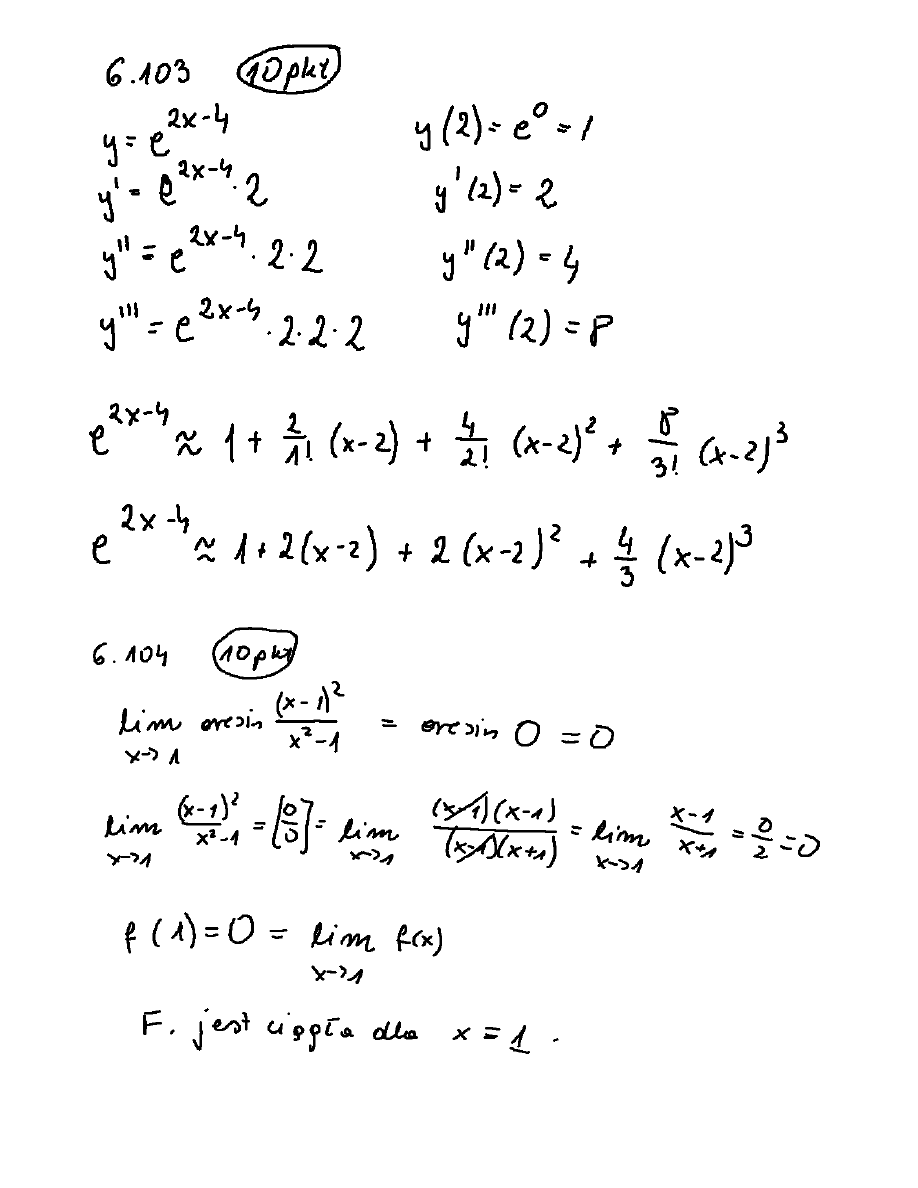

Kolokwium 1
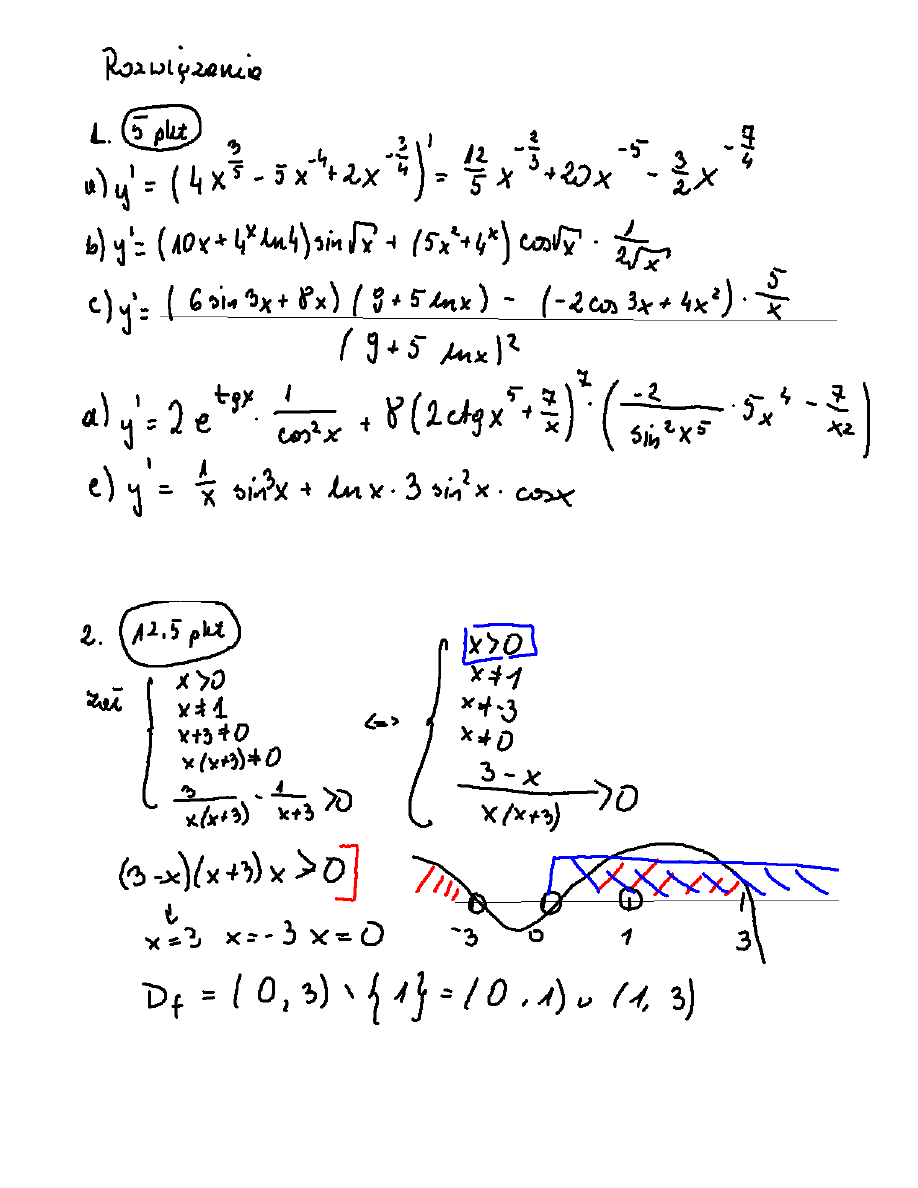
1. Policzyã pochodne funkcji : a)
4
3
4
5
3
2
5
4
x
x
x
y
,
b)
x
x
y
x
sin
4
5
2
, c)
x
ln
x
x
cos
y
5
9
4
3
2
2
, d)
8
5
7
2
2
x
ctgx
e
y
tgx
,e)
x
x
y
3
sin
ln
.
2. Wyznaczyã dziedzinê funkcji:
x
f
3
1
3
3
log
2
x
x
x
x
f
x
3. Wyznaczyã asymptoty, ekstrema i przedziaùy monotonicznoœci dla
1
)
(
2
2
x
x
x
f
.
4. Wyznaczyã wartoœã najmniejsz¹ i najwiêksz¹ funkcji
1
6
2
3
x
x
)
x
(
f
w przedziale
1
1,
.
5. Obliczyã granice: a)
1
5
2
0
x
e
x
arctgx
x
x
x
x
arcsin
sin
lim
, b)
1
2
1
3
lim
x
x
x
x
.
6 (grupa 103). Przybli¿yã funkcjê
2
x
y
ln
sum¹ 3 kolejnych potêg jednomianu
1
x
.
6. (grupa 104) . Zbadaã ci¹gùoœã funkcji
1
4
1
)
1
(
1
2
)
(
x
dla
x
dla
x
arctg
x
f
w punkcie -1 .
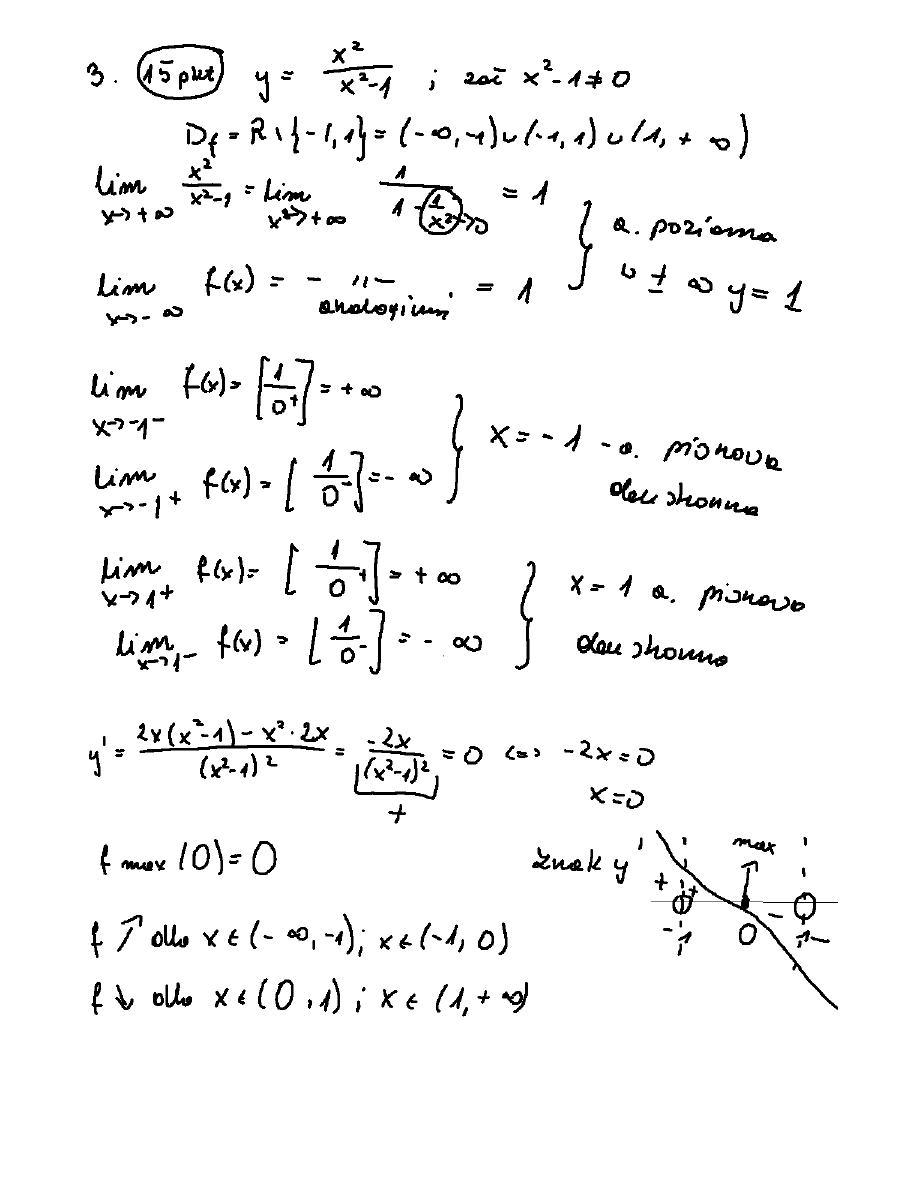
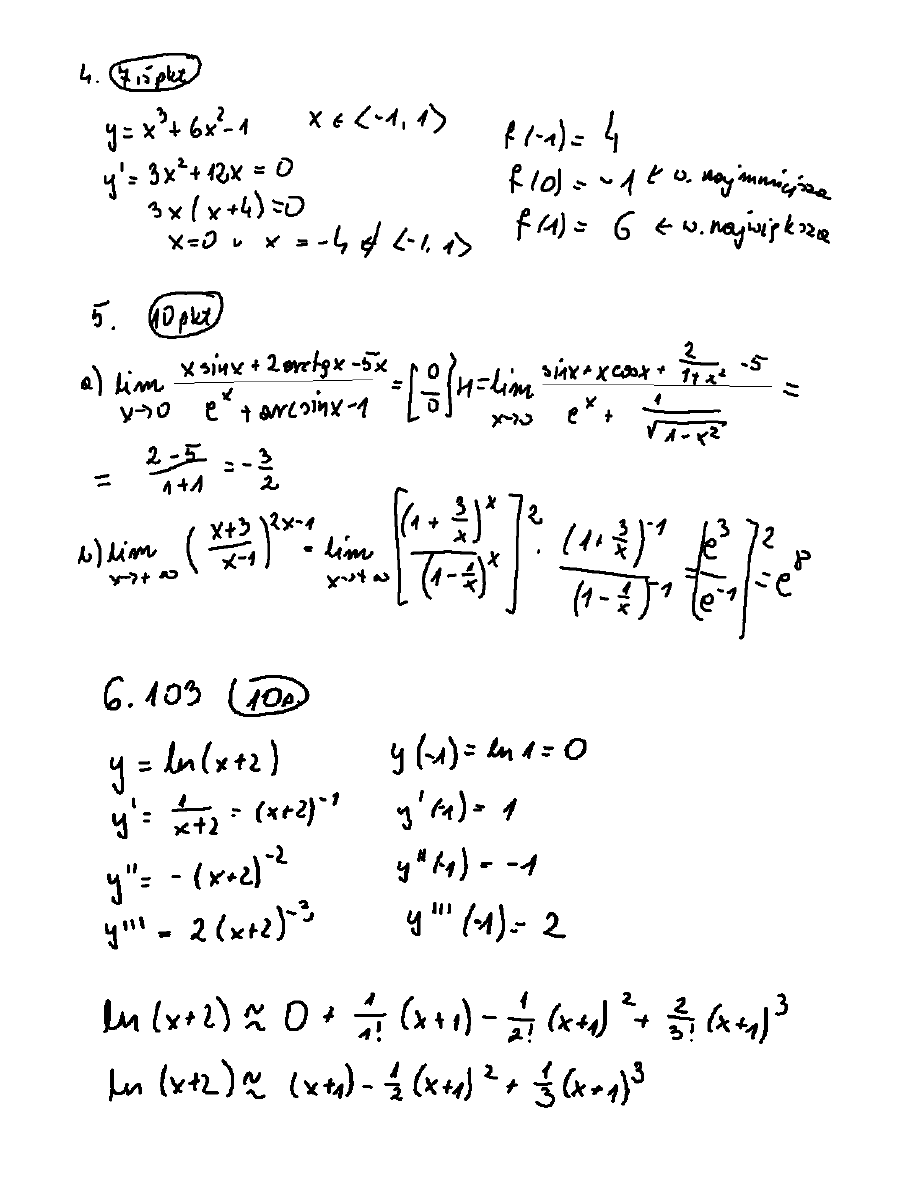
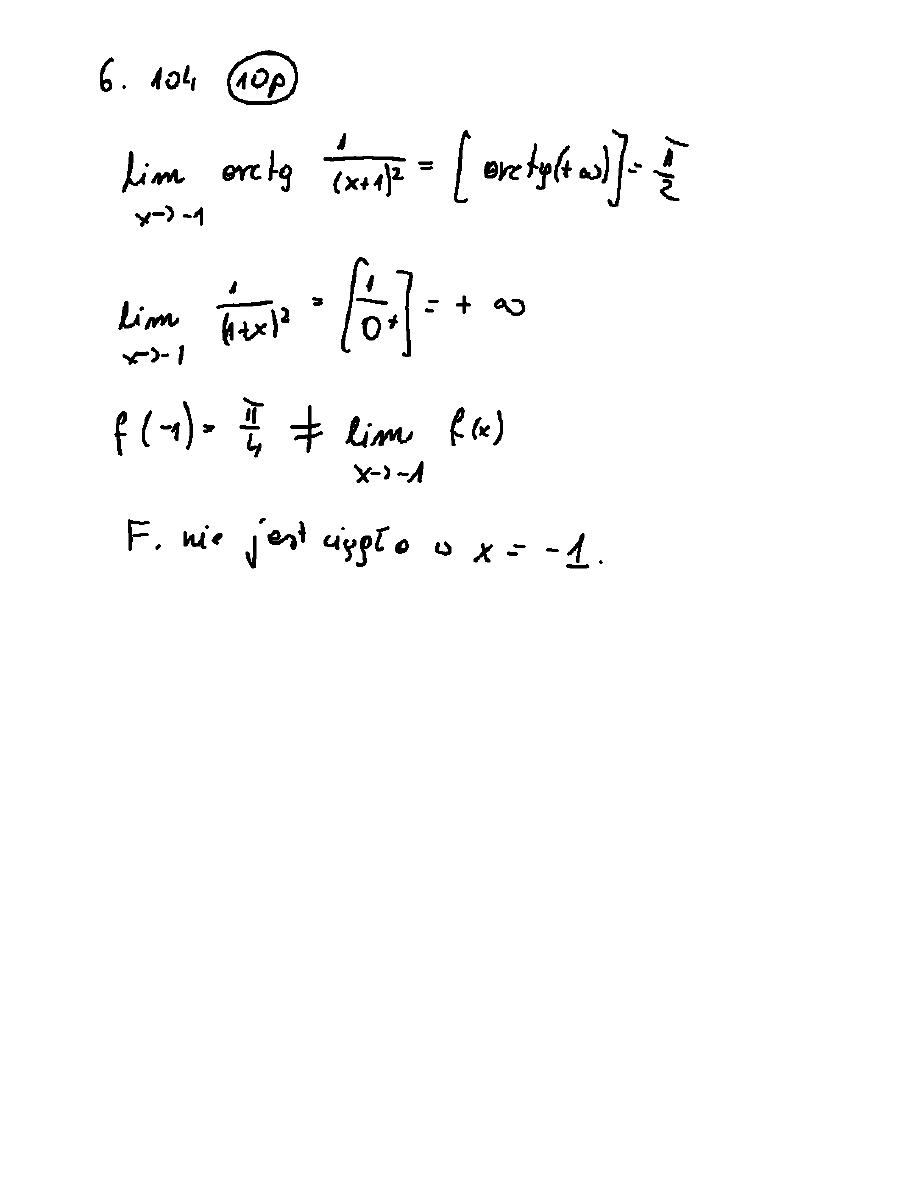
Wyszukiwarka
Podobne podstrony:
kolokwium 4 rozwiazania, Chemia
Naskręcki B, Algebra 2. Kolokwia z rozwiązaniami kolokwium4 1
kolokwium 2 rozwiazania
Lekki trening przed kolokwium rozwiazania, Semestr 5
Kolokwium 3 Rozwiązania
Naskręcki B, Algebra 2. Kolokwia z rozwiązaniami kolokwium1 1
kolokwium 3 rozwiazania, Chemia
Naskręcki B, Algebra 2. Kolokwia z rozwiązaniami kolokwium1 2
Naskręcki B, Algebra 2. Kolokwia z rozwiązaniami kolokwium3 2
Chemia - opracowania 2, PWr, Chemia, Chemia - poprzednie kolokwia i rozwiązania
kolokwium 2 rozwiazania, Chemia
Oel2-rozw, Studia Informatyka -PŁ, 2 semestr, Obwody elektryczne 2, Cwiczenia, 2 kolokwium, Rozwiąza
kolokwium rozwiazanie, Wykłady rachunkowość bankowość
kolokwium1 rozwiazania
kolokwium rozwiazania, studia, Semestr 1, Podstawy programowania 1 -PP1 Fryźlewicz Zbigniew, kolokwi
kolokwium 1 rozwiazania
więcej podobnych podstron