1

Janusz Wywiał
Katedra Statystyki
Akademia Ekonomiczna w Katowicach

Wykład 8

Zmienne losowe

Definicja: Zmienna losowa X to funkcja

spełniająca warunki:

1)

Określona

jest

na

zbiorze

zdarzeń

elementarnych i przyjmuje wartości rzeczywiste

X :

Ω

Ω

Ω

Ω

→

→

→

→

R

2)

Funkcja X jest funkcją mierzalną względem

ciała F

{w: w

∈

∈

∈

∈

Ω

Ω

Ω

Ω

, X (w) < k}

∈

∈

∈

∈

F

Zmienna losowa skokowa - skończona, bądź

przeliczalna, liczba wartości ze zbioru liczb

rzeczywistych R, które mają przyporządkowane

dodatnie prawdopodobieństwa.

2

{

}

∑

=

>

=

=

Λ

k

k

k

k

k

p

p

x

X

P

1

0

Funkcja gęstości prawdopodobieństwa ciągłej

zmiennej losowej spełnia warunki:

0

)

(

≥

Λ

∈

x

f

R

x

∫

∞

∞

−

=

1

)

(

dx

x

f

Funkcja dystrybuanty

F(x) = P{X < x}

∑

<

=

=

x

x

k

k

x

X

P

x

F

}

{

)

(

,

dla zm. skok.

3

F x

f t dt

x

( )

( )

=

−∞

∫

, dla zmiennych ciągłych

Momenty zmiennej losowej

Nadzieja matematyczna (wartość oczekiwana,

średnia, przeciętna) zmiennej losowej X:












−

=

∫

∑

∞

∞

−

dx

x

f

x

skokowe

p

x

X

E

i

i

)

(

)

(

Wariancja zmiennej losowej

[

]

(

)

(

)












−

−

=

−

=

∫

∑

∞

∞

−

dx

x

f

X

E

x

p

X

E

x

X

D

X

E

X

E

X

D

i

i

i

)

(

)

(

)

(

)

(

)

(

)

(

2

2

2

2

2

Moment zwykły rzędu r

4

m

x p

x f x dx

r

i

r

i

i

r

=















∑

∫

−∞

∞

( )

moment centralny rzędu r

(

)

(

)

c

x

m

p

x

m

f x dx

r

i

r

i

i

r

=

−

−















∑

∫

−∞

∞

1

1

( )

Szczególne przypadki: c

1

= 0

c

2

= D

2

(x)

Momenty centralne zestandaryzowane

( )

λ

r

r

r

C

C

=

2

λλλλ

1

= 0

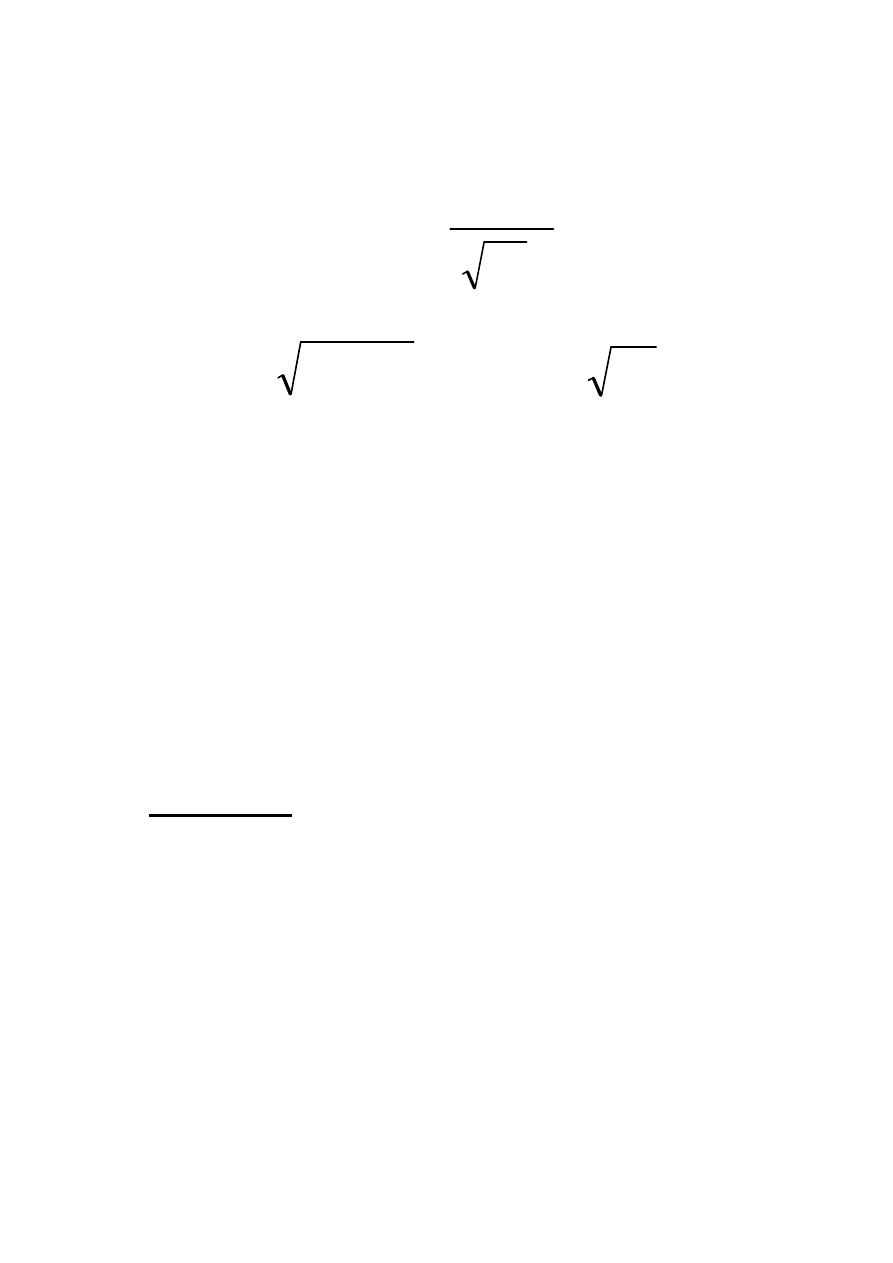
5

λλλλ

2

= 1

( )

r

r

r

C

C

2

=

λ

2

2

)

(

)

(

C

X

D

X

D

=

=

Odchylenie

standardowe

zmiennej

losowej.

Wskazuje o ile, średnio rzecz biorąc, wartości

zmiennej losowej odchylają się od jej wartości

oczekiwanej.

Dominanta

{ }

M

x p

p

d

d

k

k

=

=

:

max

- skokowe

6

M : f(M) = max

- ciągłe

Kwantyl

0 < p < 1

x

p

- kwantyl rzędu p zmiennej

losowej skokowej:

{

}

{

}









−

≥

≥

≥

≤

p

x

X

P

p

x

X

P

p

p

1

dla ciągłych zm. los.:

{

}

{

}

p

x

X

P

p

x

X

P

p

p

−

=

>

=

<

1

lub

Kwantyl rzędu 0,5 - mediana

7

Np.

rozkład

prawdopodobieństwa

wyników

egzaminu:

{

}

P X

x

x

x

x

=

=

=

=

=













0 5

3

0 4

4

0 1

5

,

,

,

F x

dla

x

dla

x

dla

x

dla

x

( )

(

,

,

( ,

,

( ,

(5,

)

=

∈ −∞ >

∈

>

∈

>

∈ +∞

















0

3

0 5

3 4

0 9

4 5

1

E(X) = 3

⋅⋅⋅⋅

0,5 + 4

⋅⋅⋅⋅

0,4 + 0,1

⋅⋅⋅⋅

5 = 1,5 + 1,6 + 0,5 = 3,6

Średnio rzecz biorąc ocena z egzaminów wynosi

3,6 (wartość oczekiwana z egzaminu wynosi 3,6).

D

2

(X)=(3-3,6)

2

⋅

0,5+(4-3,6)

2

⋅

0,4+(5-3,6)

2

⋅

0,1=0,44

D(x)≈0,7.

8

Własności funkcji dystrybuanty

1.

Funkcja niemalejąca

2.

Przynajmniej lewostronnie ciągła

3.

Granica

lim

( )

lim

( )

x

x

F x

F x

→−∞

→+∞

=

∧

=

0

1

Rozklad hipergeometryczny:

Mamy urnę z kulami: B - białymi i C - czarnymi,

C+B=N. Losujemy z niej n kul

{

}

P H

k

B

k

C

n

k

N

n

=

=











−





















E H

n

B

N

D

H

N

n

N

n

B

N

B

N

( )

,

( )

(

)

=

=

−

−

−











2

1

1

9

Jeśli będziemy losować ze zwrotem kule do urny

oraz

p

B

N

=

, to funkcja prawdopodobieństwa

rozkładu dwumianowego ma postać:

{

}

P X

k

n

k

p

p

k

n

k

n k

=

=











−

=

−

(

)

,

, , ,...

1

0 1 2

gdzie wartości k zmiennej losowej X

n

, to liczba

wylosowanych kul białych.

E(X

n

) = np, D

2

(X

n

) = np (1 - p)

Jeśli n

→

→

→

→∞

∞

∞

∞

i p

→

→

→

→

0, tak że np=

λλλλ

, to

{

}

{

}

lim

!

n
p

n

k

P X

k

P Y

k

k

e

→∞

→

−

=

=

=

=

0

λ

λ

Jest to funkcja prawdop. rozkładu Poissona.

E(Y) =

λλλλ

,

D

2

(Y) =

λλλλ

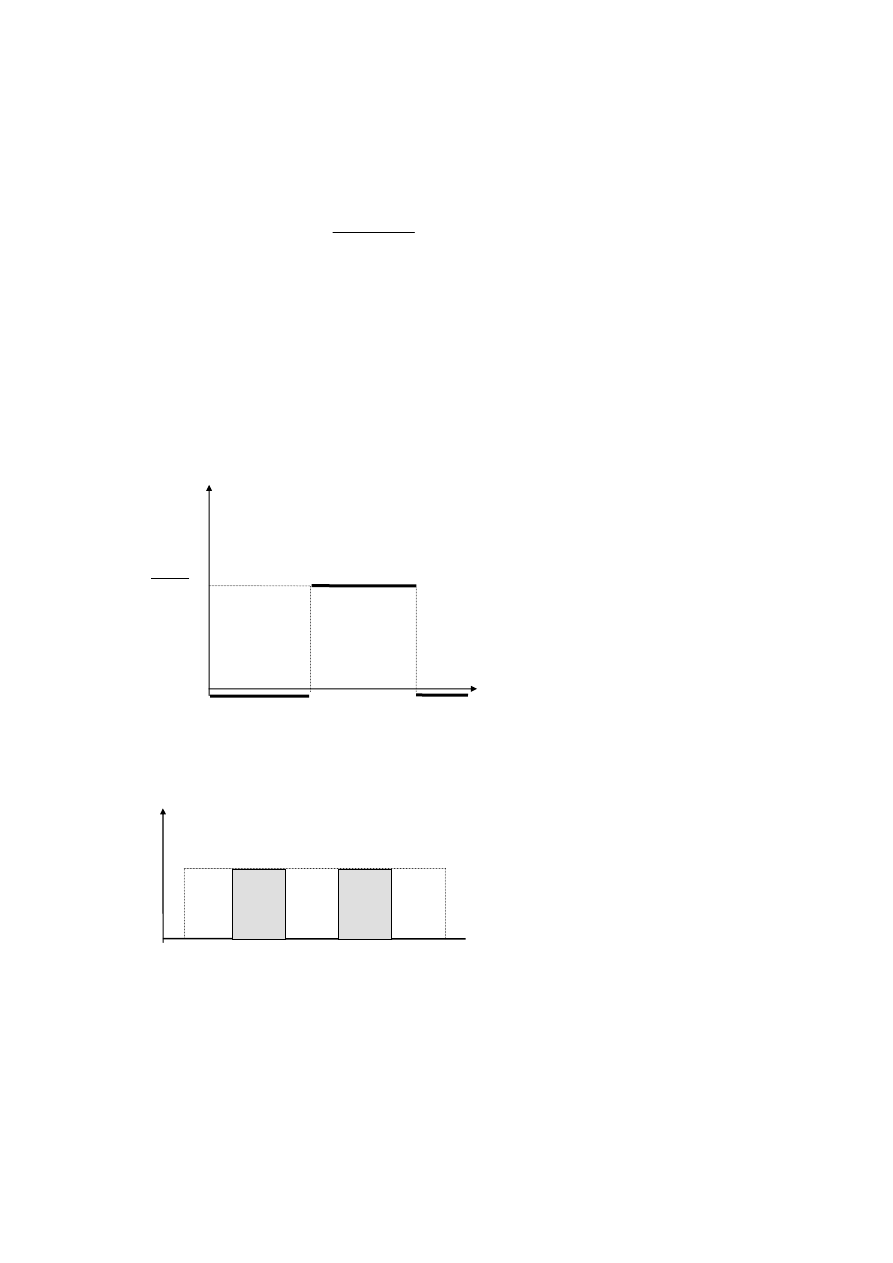
10

Rozkład jednostajny ma funkcję gęstości:

f x

b

a

dla

x

a b

dla

x

a b

( )

,

,

=

−

∈<

>

∉<

>











1

0

f(x)

a

b x

∆∆∆∆

∆∆∆∆

6

6

6

67

7

7

78

8

8

8

6

6

6

67

7

7

78

8

8

8

a x

1

x

1

+

∆∆∆∆

x

2

x

2

+

∆∆∆∆

b

Zakreskowane pole będzie const. dla dowolnych

punktów x

1

, x

2

, takich, że x

i

≤b-

∆∆∆∆

.

1

b

a

−

11

P{x

1

< X < x

1

+

∆∆∆∆

} = P{x

2

< X < x

2

+

∆∆∆∆

}, x

1

≠≠≠≠

x

2

.

Niech czas oczekiwania na obsługę w

Supersamie ma rozkład wykładniczy:

g x

e

dla

x

dla

x

x

( )

=

≥

<








−

α

α

0

0

0

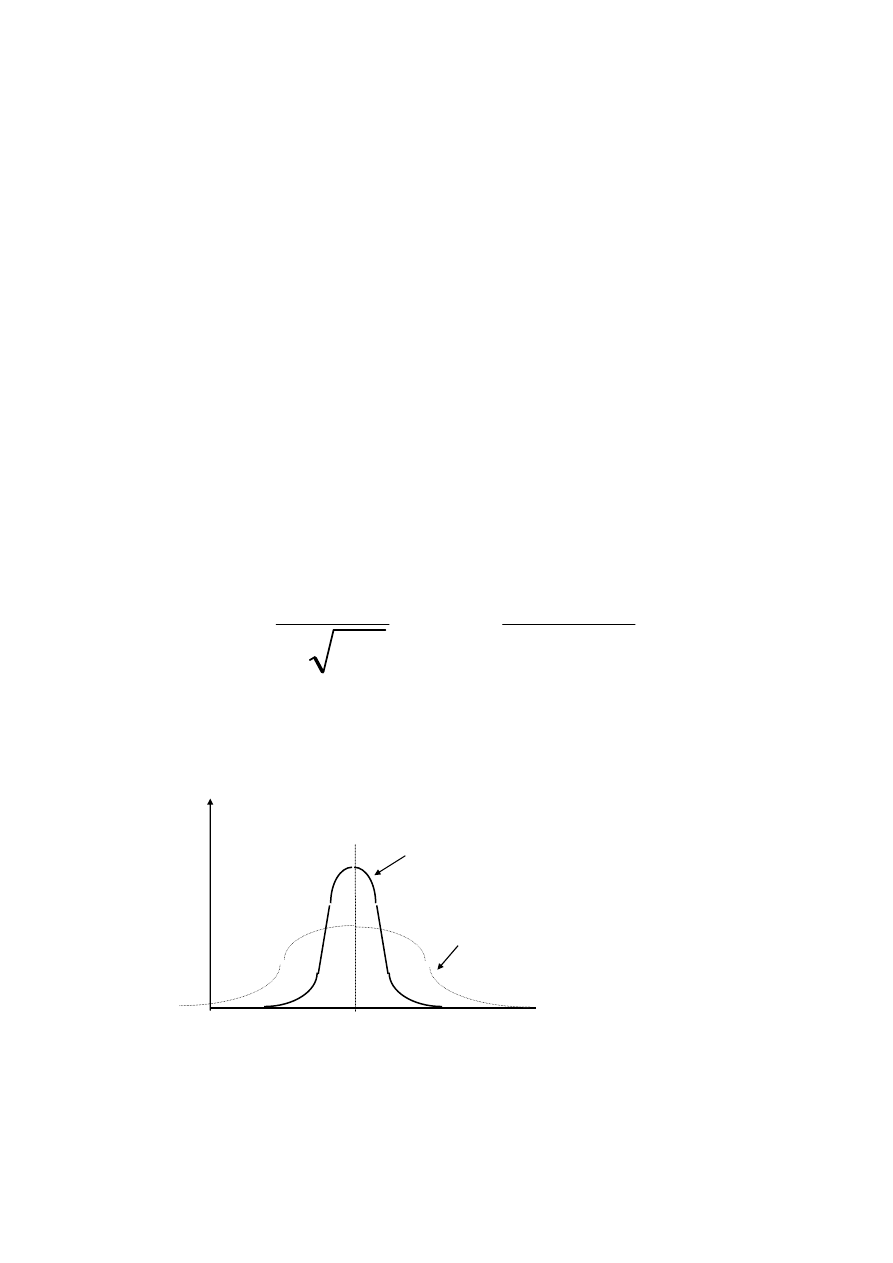
12

{

}

P x

X

x

f x dx

x

x

1

1

1

1

< <

+

=

=

+

∫

∆∆∆∆

∆∆∆∆

( )

(

) ( )

=

−

=

+

−

−∞

−∞

+

∫

∫

f x dx

f x dx

F x

F x

x

x

( )

( )

1

1

1

1

∆∆∆∆

∆∆∆∆

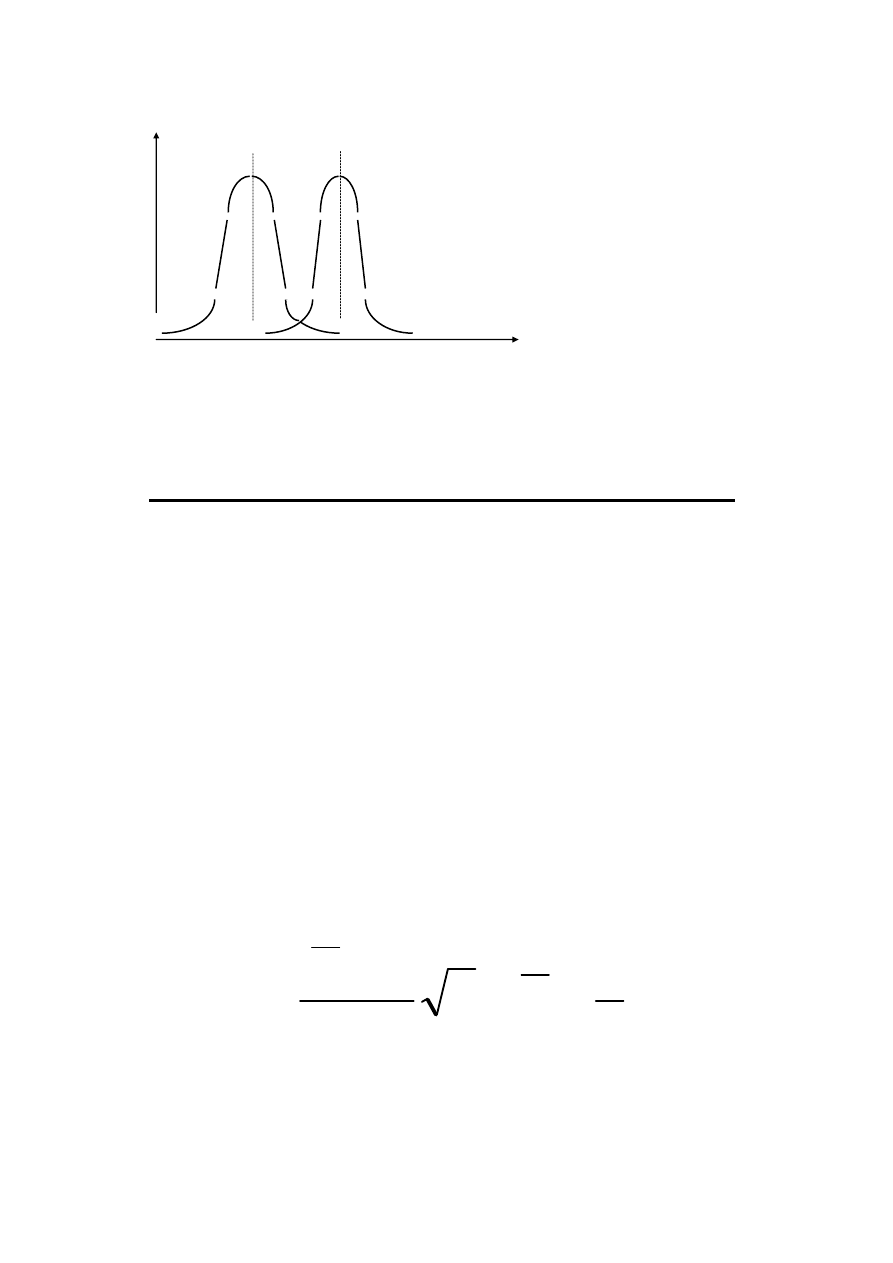
Rozkład normalny

(

)

,

2

exp

2

1

)

(

2

2













−

−

=

σ

µ

π

σ

x

x

f

σσσσ

1

σσσσ

2

>

σσσσ

1

µµµµ

( )

σ

µ

σ

µ

=

=

)

(

,

)

(

,

,

~

X

D

X

E

N

X

13

µµµµ

1

µµµµ

2

µµµµ

1 <

µµµµ

2

Graniczne twierdzenie Lindeberga - Levye’go

Założenia:

1.

Zmienne losowe X

1

, X

2

, ..., X

n

są niezależne

2.

Każda z nich ma taki sam rozkład, przy czym

( )

( )

2

2

,...,

1

δ

µ

=

∧

=

Λ

=

i

i

n

i

X

D

X

E

Niech

∑

=

=

−

=

n

i

i

n

X

n

X

n

X

Z

1

1

,

δ

µ

14

Wówczas

(

)

( )

)

(

lim

lim

z

z

F

z

Z

P

n

n

n

n

ϕ

=

=

<

∞

→

∞

→

,

gdzie Z ma rozkład normalny, standardowy, czyli

Z ~ N(0,1)

lub

(

)

( )

)

(

lim

lim

u

F

u

F

u

X

P

n

n

n

n

=

=

<

→∞

→∞

,

gdzie U ma rozkład normalny:













n

N

2

,

σ

µ

.

u<-matrix(0,10000,1)
for (i in 1:10000) u[i]<-mean(runif(n,a,b))
hist(u)