Ćwiczenie 6

Temat:

BADANIE CEWKI Z RDZENIEM

FERROMAGNETYCZNYM

I. ZAGADNIENIA

1.

Badanie pętli histerezy za pomocą oscyloskopu.

2.

Analiza harmonicznych prądu magnesującego dławika.

3.

Wyznaczenie parametrów schematu zastępczego dławika.

II. WIADOMOŚCI PODSTAWOWE

Dławikiem nazywamy cewkę z rdzeniem ferromagnetycznym.

Wprowadzenie rdzenia ferromagnetycznego jest źródłem nieliniowości
charakterystyki magnesowania.

Zależność pomiędzy napięciem U zasilającym dławik ze „sztywnego”

źródła a maksymalną wartością strumienia

φ

m w rdzeniu podana jest

zależnością:

U = 4,44

φ

m

. z f

(6.1)

gdzie: z - liczba zwojów cewki, f - częstotliwość zasilania.

Jeżeli zasilimy dławik napięciem sinusoidalnym U takim, że

odpowiadająca mu maksymalna wartość strumienia

φ

m. znajduje się

w obszarze nasycenia magnetycznego rdzenia, to prąd magnesujący rdzeń jest
niesinusoidalny.
Charakterystyczną cechą dławika jest pętla histerezy materiału rdzenia, która
również wpływa na niesinusoidalność prądu dławika. Moc wydzielana w
rdzeniu w postaci ciepła, zużywana na przemagnesowanie rdzenia, jest
proporcjonalna do pola pętli histerezy.

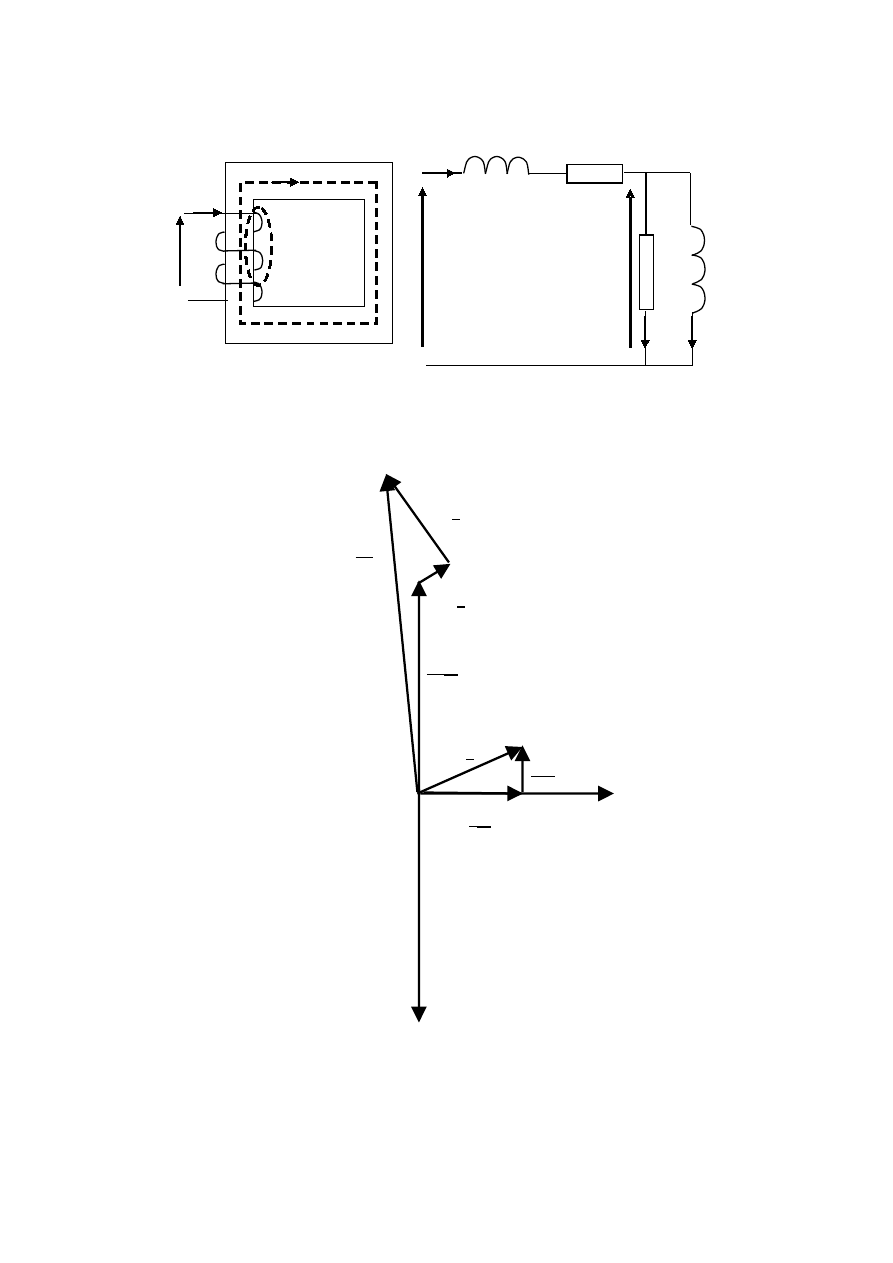
1. Schemat zastępczy dławika

Schemat zastępczy dławika przedstawiono na rys. 6.1, na którym :

X

s

- reaktancja rozproszenia, R - rezystancja uzwojenia, R

Fe

- rezystancja

charakteryzująca straty mocy czynnej w rdzeniu, X

µ

- reaktancja magnesowania,

charakteryzuje straty mocy biernej, I

µ

- prąd magnesujący - składowa bierna

prądu dławika, I

fe

- prąd strat w rdzeniu - składowa czynna prądu dławika.

6-1

Φ

Φ

3

z

i

U

I

U

X

S

R

R

FE

X

µ

U

µ

I

µ

I

FE

Rys. 6.1

2. Wykres wektorowy dławika przedstawia rys. 6.2

Rys. 6.2

jX

S

I

U

µ

U

RI

I

I

µ

I

FE

Φ

m

6-2

3. Analiza harmoniczna przebiegów odkształconych

Prąd magnesujący dławika jest przykładem przebiegu periodycznego

niesinusoidalnego.

ODKSZTAŁCENIE KRZYWEJ PRĄDU

Jeżeli do uzwojenia nawiniętego na rdzeń ferromagnetyczny

doprowadzimy napięcie sinusoidalne zmienne, to w uzwojeniu popłynie prąd
niesinusoidalny. Odkształcenie krzywej prądu jest spowodowane nieliniową
charakterystyką B = f(H) rdzenia. Można przy tym wyróżnić dwa zasadnicze
przypadki:

-przebieg prądu przy pominięciu zjawiska histerezy magnetycznej;
-przebieg prądu przy uwzględnieniu zjawiska histerezy magnetycznej;
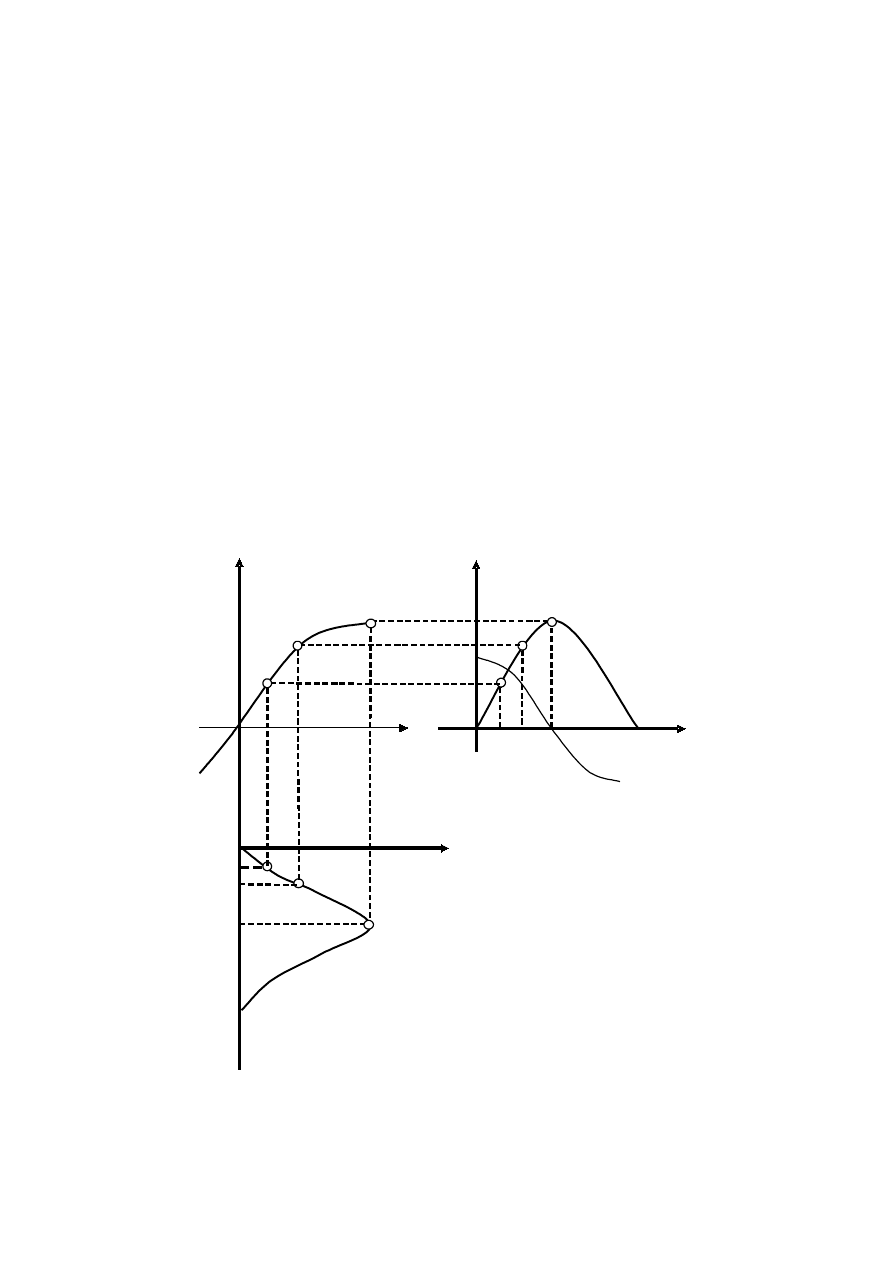
W pierwszym przypadku krzywa B = f(H) ma postać pokazaną na rys. 6.3.

Jest to jednocześnie charakterystyka

φ

= f1(i), gdyż strumień jest proporcjonalny

do indukcji B, a zgodnie z prawem przepływu istnieje bezpośrednia zależność
natężenia pola magnetycznego w rdzeniu od prądu przepływającego
w uzwojeniu.

2’

1’

3’

1

2

u

Φ

3

Φ

;u

Φ

1

Φ

2

Φ

3

Φ

;B

0

t

2

t

3

t

1

t

3

t

2

t

1

1’’

2’’

3’’

t

i;H

i

1

i

2

i

3

Rys.6.3 Wykreślenie przebiegu prądu w cewce z rdzeniem ferromagnetycznym

przy pominięciu zjawiska histerezy magnetycznej.

6-3

2’

3’

Φ

;B

0’

t

5

t

2

t

1

1’’

2’’

t

3

i;H

i

5’

4’

6’

0’’

3’’

4’’

5’’

6’’

t

0

t

6

1

2

0

3

Φ

;u

t

2

t

3

t

1

t

4

5

6

u

t

4

t

5

t

6

t

0

Φ

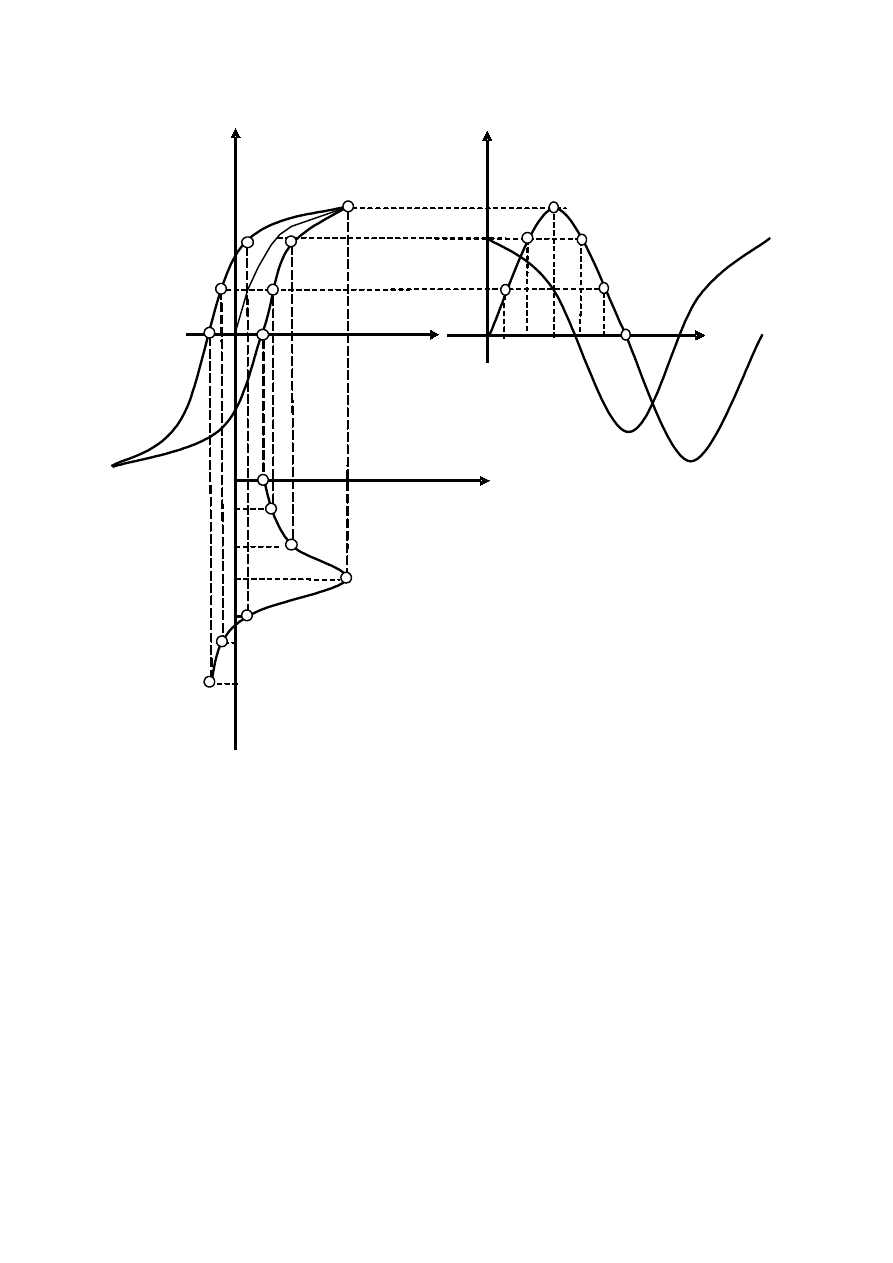
Rys.6.4 Wykreślenie przebiegu prądu w cewce z rdzeniem ferromagnetycznym

przy uwzględnieniu zjawiska histerezy magnetycznej.

Załóżmy, że napięcie doprowadzone do zacisków uzwojenia u = Um sin(

ω

t +

α

)

, przy czym

α

=

π

/2. Zgodnie z zależnością u = z(d

φ

/ dt), otrzymamy

φ

=

φ

m.

sin

ω

t. Na rys 6.3 wykreślono przebieg napięcia na zaciskach uzwojenia i

strumienia w rdzeniu. Dla poszczególnych czasów t1, t2, t3,... znajdujemy
wartości strumienia magnetycznego

φ

1.,

φ

2 i

φ

3 (punkty 1,2,3 ...). Punkty te

rzutujemy na charakterystykę

φ

(i) otrzymując punkty 1’, 2’, 3’... Wartościom

strumienia w poszczególnych chwilach odpowiadają wartości prądów i1, i2, i3.
Nanosząc otrzymane wartości prądów na charakterystykę i = f(t) (punkty 1”, 2”,
3”) uzyskujemy poszukiwany przebieg prądu w uzwojeniu. Prąd ten jest
odkształcony i tym bardziej odbiega od przebiegu sinusoidalnego im bardziej
nieliniowa jest charakterystyka strumienia w funkcji prądu i im większe jest
nasycenie rdzenia.

6-4

W identyczny sposób konstruuje się krzywą prądu przy uwzględnieniu

zjawiska histerezy magnetycznej. Z rysunku 6.4 wynika, że jeśli uwzględnić
zjawisko histerezy, prąd w chwili t = 0 nie przechodzi przez zero.

Każdą funkcję okresową, spełniającą warunki Dirichleta, możemy

przedstawić w postaci szeregu harmonicznego nieskończonego, zwanego
szeregiem Fouriera. Szereg harmoniczny w postaci trygonometrycznej możemy
zapisać następująco:

f x

A

kx

k

k

( )

sin(

)

=

+

ϕ

W przypadku przebiegu określonego krzywą doświadczalną stałe rozwinięcia w
szereg można obliczyć za pomocą wzorów przybliżonych :

A

m

f x

o

i

i

m

=

=

∑

1

2

1

2

( )

gdzie : 2m. -liczba części na jaką został podzielony okres przebiegu :

a

m

f x

kx

k

i

i

m

i

=

=

∑

1

1

( ) cos

b

m

f x

kx

k

i

i

m

i

=

=

∑

1

1

( ) sin

A

a

b

k

k

k

=

+

2

2

ϕ

k

k

k

arctg

a

b

=

4.

Pętla Histerezy

Materiały magnetyczne, z których wykonuje się elementy obwodu

magnetycznego dzielimy na:

-materiały magnetyczne miękkie
-materiały magnetyczne twarde

Przy wzroście natężenia pola magnetycznego indukcja zmienia się według

krzywej magnesowania pierwotnego zaś przy zmniejszaniu tego natężenia
funkcja B = f(H) zmienia się wzdłuż innej krzywej. Zjawisko to nosi nazwę
histerezy magnetycznej. Stan rdzenia, przy którym zwiększenie natężenia pola
magnetycznego daje nieznaczny wzrost indukcji magnetycznej nazywa się
stanem nasycenia.

6-5

Przy wielokrotnym przemagnesowaniu materiału magnetycznego

charakterystyka B = f(H) jest krzywą zamkniętą, zwaną pętlą histerezy - rys. 6.5
, na którym :Br - indukcja magnetyczna szczątkowa, Hc - natężenie korekcyjne.

B

-B

r

-H

C

B

r

H

C

H

Rys. 6.5

Materiały magnetycznie miękkie (żelazo elektrolityczne, stal krzemowa,

stopy żelazoniklowe) mają wąską pętlę histerezy. Materiały te stosuje się do
wyrobu blach transformatorowych i blach twornikowych.

Materiały magnetycznie twarde (stal węglista, stal chromowa, stal

kobaltowa) mają szeroką pętlę histerezy. Stosowane są one do wyrobu rdzeni
magnesów trwałych.

6-6

III. Pomiary

1.

Wyznaczanie parametrów układu zastępczego dławika

1.1

Połączyć układ pomiarowy jak na rys. 11.4.

U

A

V

W

D

AT

Rys. 6.6

1.2

Pomiar rezystancji dławika wykonać za pomocą omomierza.

1.3 W układzie jak na rys.6.6 zmierzyć napięcie, prąd oraz moc czynną

pobieraną przez dławik.

[Aby otrzymać moc czynną pobieraną przez dławik należy od mocy
wskazywanej przez watomierz odjąć moc pobieraną przez uzwojenie
napięciowe watomierza i woltomierza.

P

P

U

R

U

R

d

Wt

V

=

−

−

2

2

U - wskazanie woltomierza
RW - rezystancja uzwojenia napięciowego watomierza
RV - rezystancja woltomierza
Moc czynna pobierana przez dławik składa się z mocy traconej w
rezystancji uzwojenia i strat w rdzeniu.

P

P

P

d

u

Fe

=

+

P

P

P

P

RI

Fe

d

u

d

=

−

=

−

2

R - rezystancja uzwojenia
Pomijając indukcyjność cewki od strumienia rozproszenia można
obliczyć wartości pozostałych elementów schematu zastępczego
dławika: G

Fe

,R

Fe

, B

µ

X

µ

1.4 Pomiary wykonać dla trzech napięć zasilających, a następnie obliczyć

parametry schematu zastępczego dławika.

2.

Zaobserwować na ekranie oscyloskopu przebieg napięcia zasilającego
dławik.

2.1

Badanie przebiegu napięcia proporcjonalnego do prądu magnesującego
dławika.

Zmontować układ pomiarowy jak na rys. 6.7.

6-7

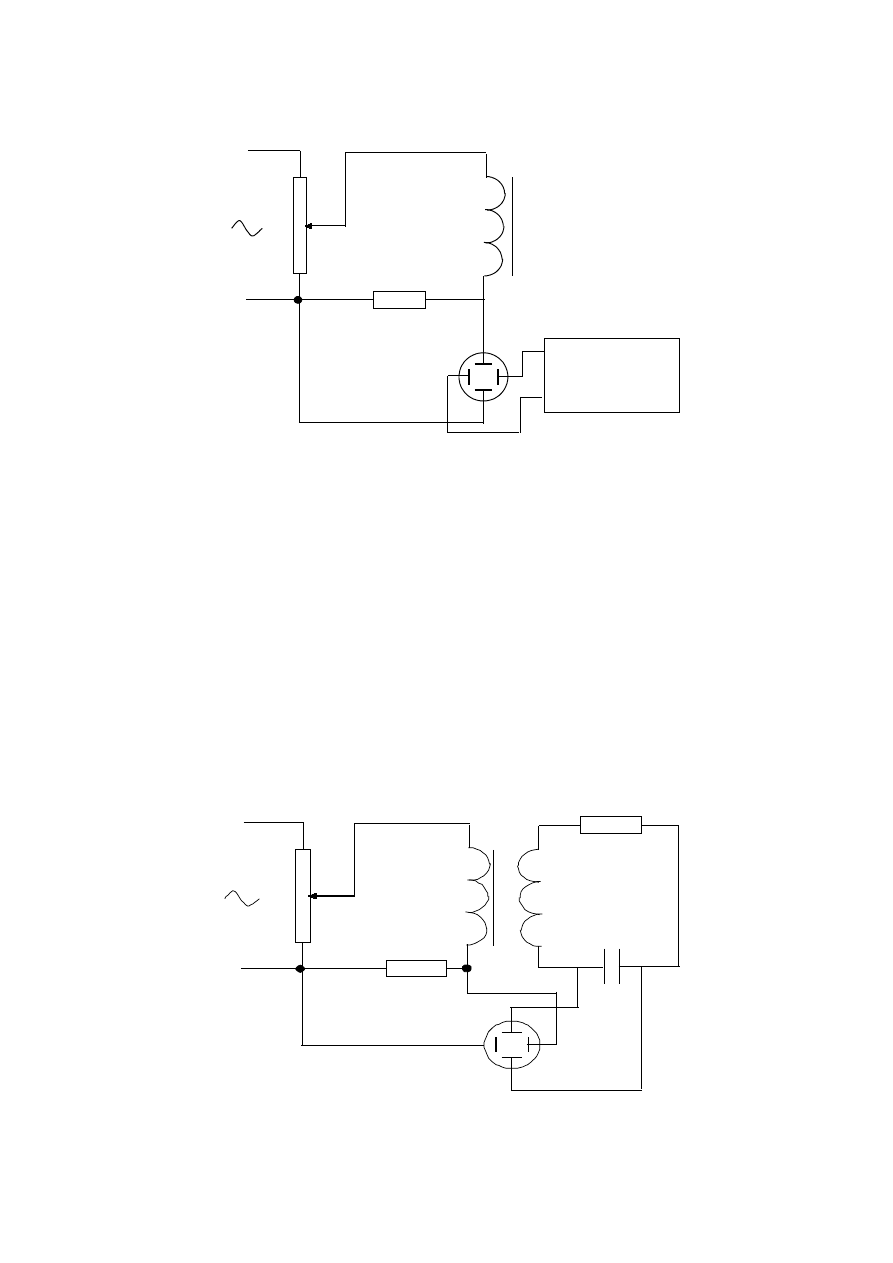
D

AT

R

Generator

podstawy

czasu

Rys. 6.7

2.2 Zaobserwować na oscyloskopie przebieg napięcia proporcjonalnego do

prądu magnesującego dławika dla małych i dużych napięć zasilających.

2.3 Uzasadnić otrzymany na ekranie kształt przebiegu.
2.4 Otrzymany przebieg periodyczny niesinusoidalny przerysować.
2.5 Określić do jakiej grupy funkcji zaliczyć można przebieg odkształcony

i wykorzystać wynikające stąd uproszczenia w obliczeniach.

2.6 Korzystając z zależności U = f(

φ

m

) określić

ψ

m

., powyżej którego zaczyna

występować nasycenie magnetyczne rdzenia

3.

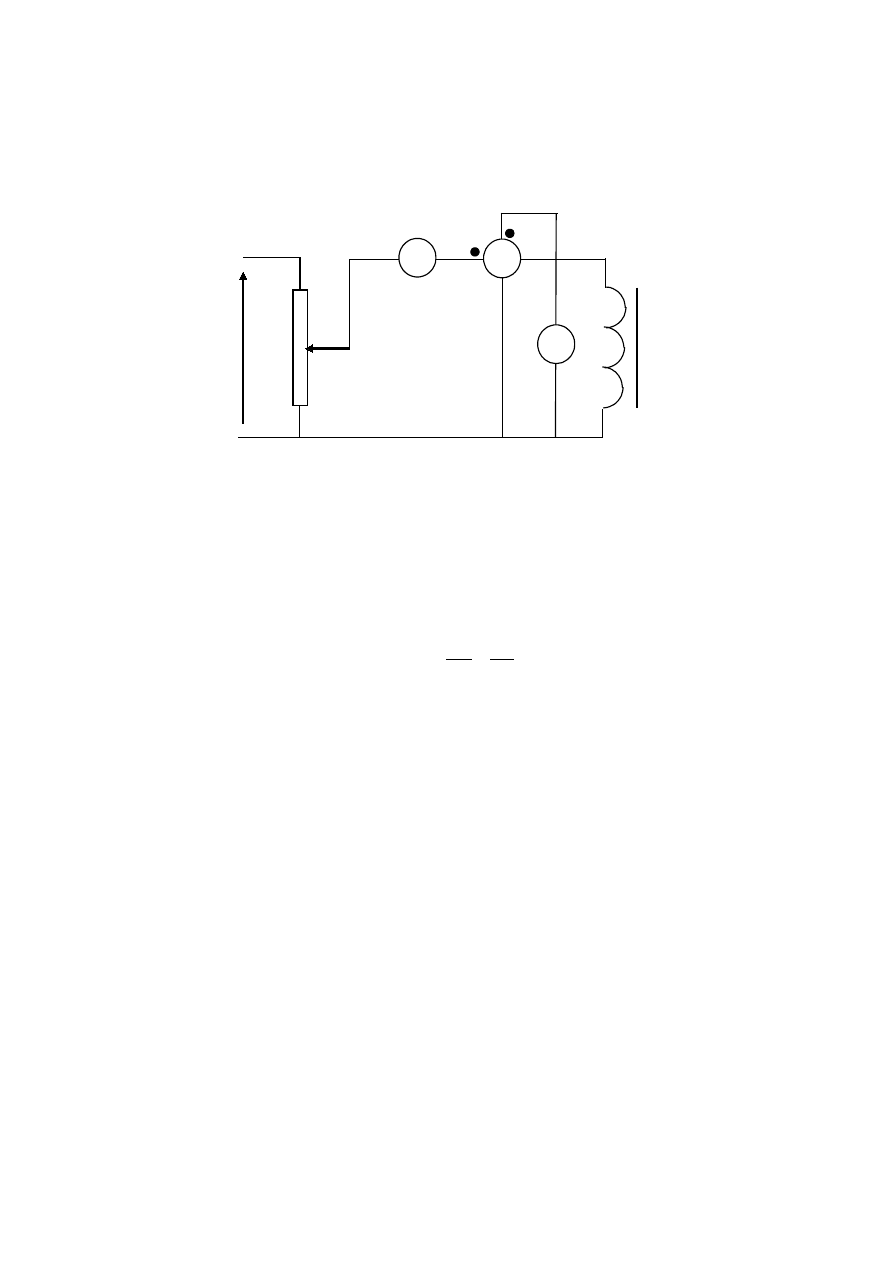
Badanie pętli histerezy za pomocą oscyloskopu

3.1 Zmontować układ pomiarowy jak na rys. 6.8
3.2 Zobrazować pętlę histerezy rdzenia dławika i otrzymany obraz

przerysować

AT

R

1

R

2

C

2

Rys 6.8

6-8

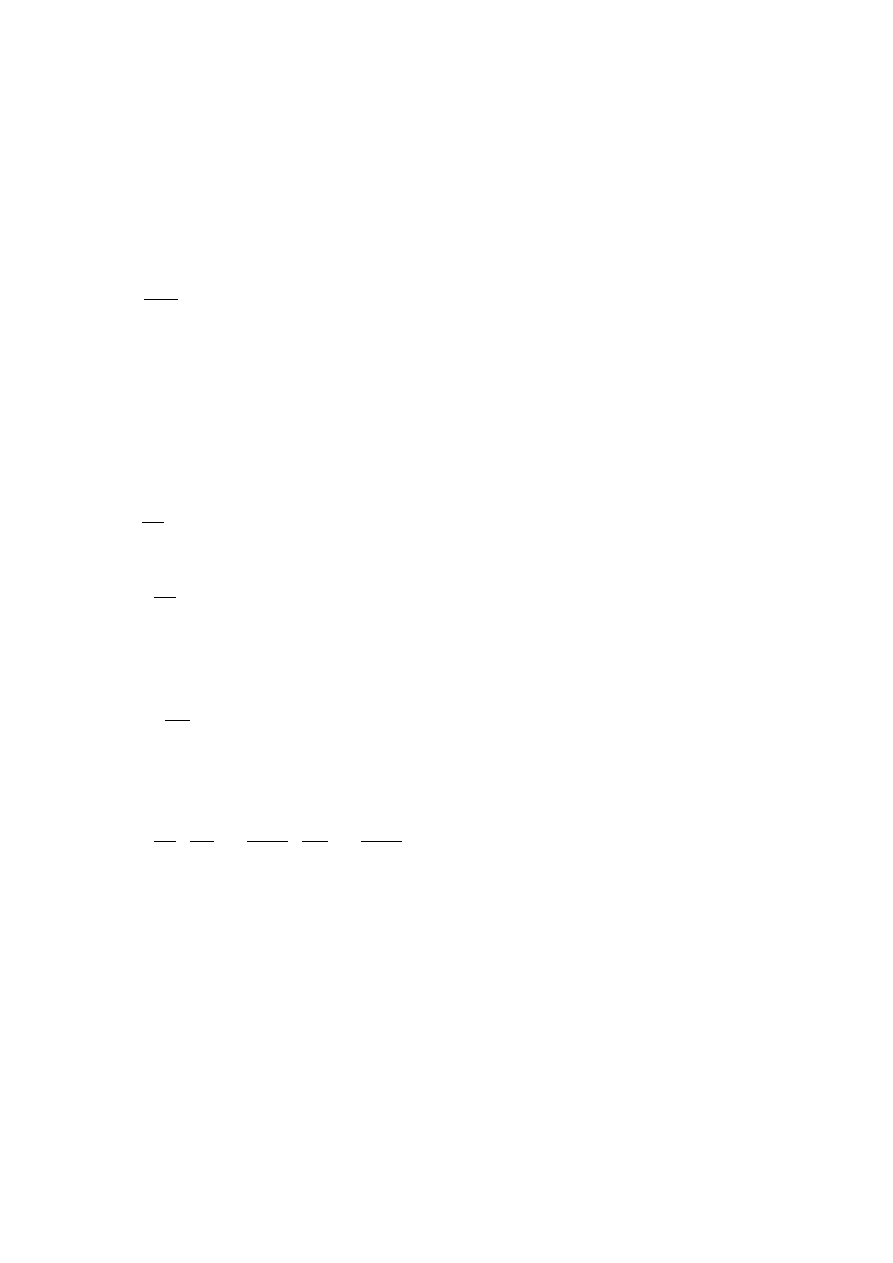
OPIS UKŁADU CAŁKUJĄCEGO R

2

C

2

Jeżeli są spełnione następujące warunki:

2

2

1
C

R

ω

〉 〉

r

R

〉 〉

2

gdzie ω – pulsacja podstawowej harmonicznej napięcia U

2

indukowanego w

uzwojeniu z

2

, r – rezystancja cewki z

2

, oraz jeśli pominiemy indukcyjność

rozproszenia cewki z

2

, to można napisać:

2

2

2

R

U

i

=

∫

=

dt

i

C

u

C

2

2

2

1

Korzystając z prawa indukcji elektromagnetycznej:

dt

d

z

u

Φ

=

2

2

otrzymamy:

Φ

=

Φ

=

Φ

=

=

∫

∫

1

2

2

2

2

2

2

2

2

2

2

1

k

R

C

z

dt

dt

d

R

C

z

dt

R

U

C

u

C

6-9