Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
1
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
B A D A N I A O P E R A C Y J N E
ANALITYCZNE MODELE ELEMENTARNEGO
SYSTEMU MASOWEJ OBSŁUGI
M/M/1/∞
Materiały pomocnicze do wykładu
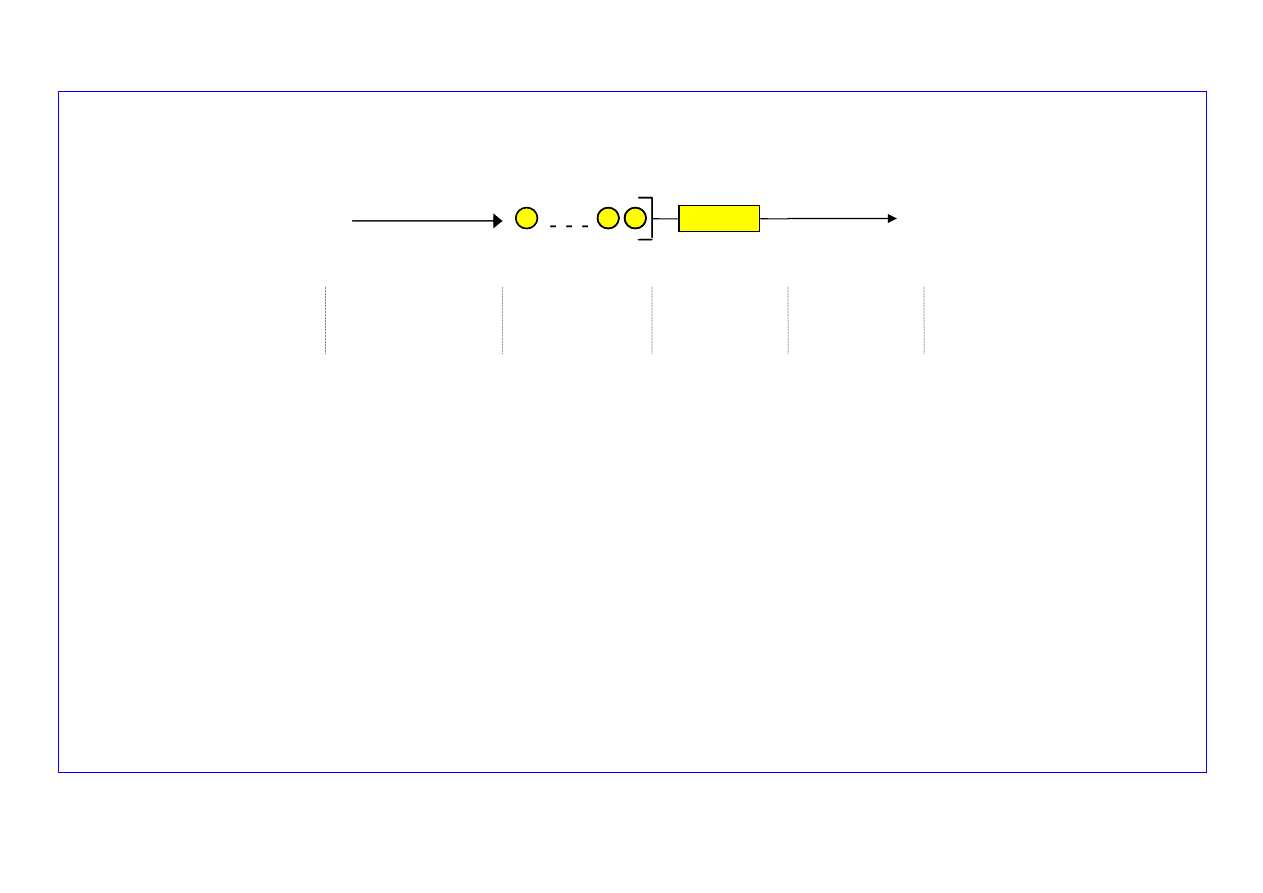
POJĘCIE SYSTEMU M/M/1/
∞
PRZYKŁADY
−
Stanowisko diagnostyczne;
−
Mały warsztat samochodowy;
−
Myjnia samochodowa;
−
Automat telefoniczny;
−
Gabinet lekarski specjalistyczny;
−
Kiosk.
Strumień
zgłoszeń
Poissona
Kolejka
Stanowisko
obsługi
∞
2
1
Strumień
wyjściowy
μ
λ
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
2
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
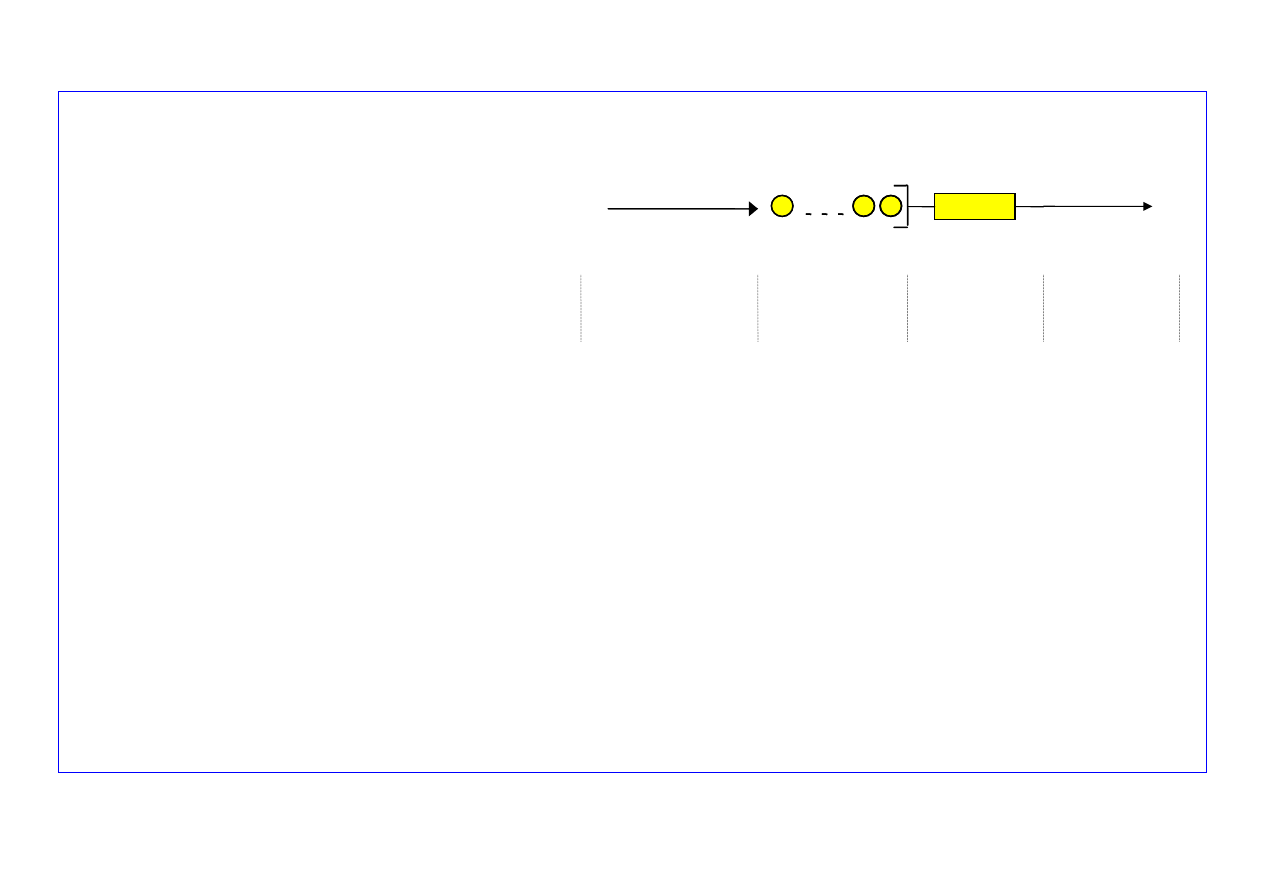
ZAŁOŻENIA M/M/1/
∞
−
Strumień zgłoszeń jest strumieniem Poissona o intensywności
λ
, czyli odstępy między
zgłoszeniami opisuje rozkład wykładniczy o funkcji gęstości prawdopodobieństwa:
( )
t
e
t
f
⋅
−
⋅
=
λ
λ
−
−
Stanowisko obsługowe ma jeden kanał obsługi;
Czas obsługi zgłoszeń opisuje rozkład wykładniczy o funkcji gęstości prawdopodobieństwa:
( )
τ
μ
μ
τ
⋅
−
⋅
=
e
f
−
Kolejka posiada nieograniczoną liczbę miejsc przeznaczonych na oczekiwanie zgłoszeń
(obiektów).
Strumień
zgłoszeń
Poissona
Kolejka
Stanowisko
obsługi
∞
2
1
Strumień
wyjściowy
μ
λ
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
3
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
POSZUKIWANE
○ Stany systemu;
○ Graf stanów systemu;
○ Stacjonarne prawdopodobieństwa stanów systemu;
○ Średnia liczba zgłoszeń w systemie;
○ Średnia liczba zgłoszeń oczekujących w kolejce;
○ Średnia liczba obsługiwanych zgłoszeń w systemie.
Strumień
zgłoszeń
Poissona
Kolejka
Stanowisko
obsługi
∞
2
1
Strumień
wyjściowy
μ
λ
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
4
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
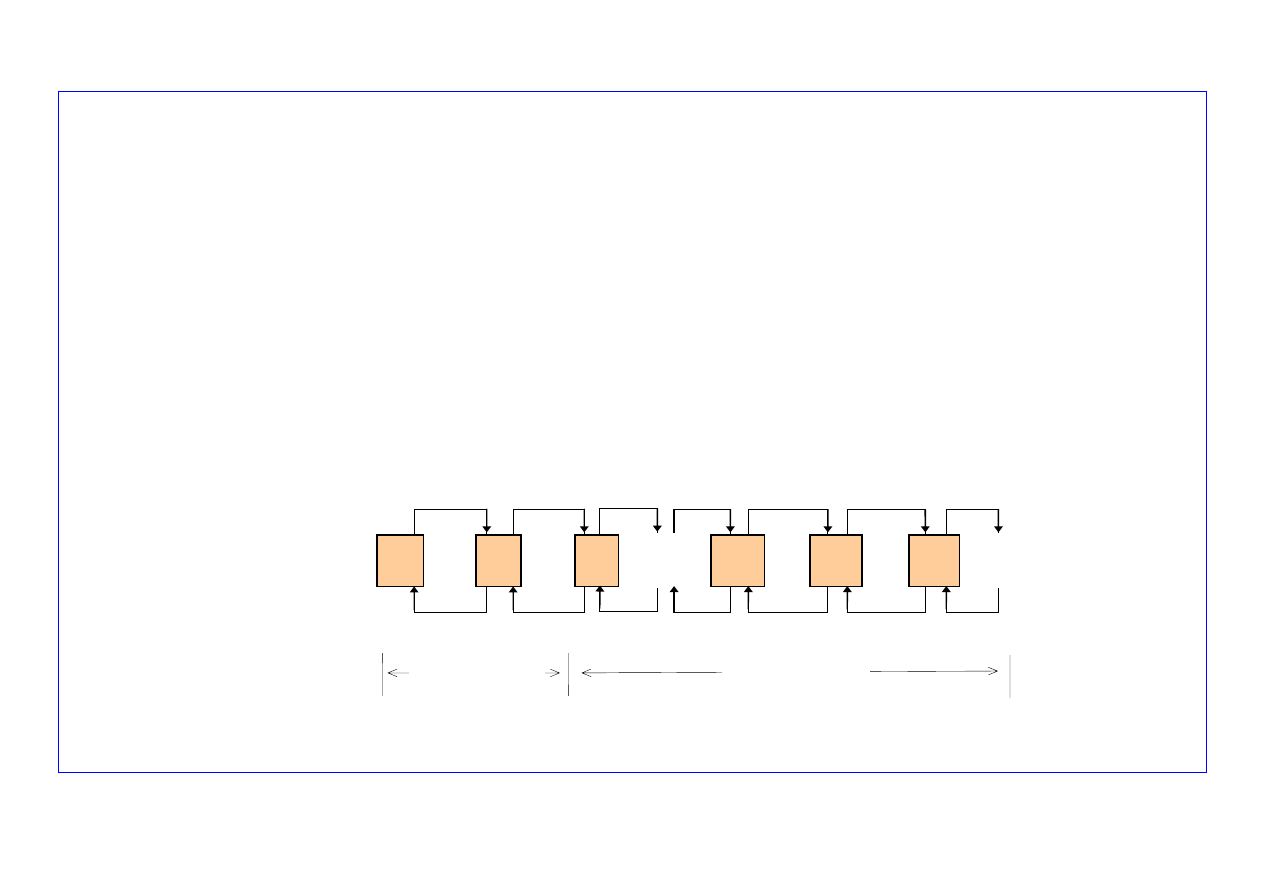
ROZWIĄZANIA
○
Stany systemu
S
0
− w systemie nie ma zgłoszeń,
S
1
− jedno zgłoszenie znajduje się w systemie i następuje jego obsługa na pierwszym
i jedynym kanale obsługowym, kolejka nie występuje,
S
2
− dwa zgłoszenia znajdują się w systemie, pierwsze jest obsługiwane, drugie czeka
w kolejce,
S
k
− k zgłoszeń znajduje się w systemie, pierwsze jest obsługiwane, pozostałe k
−
1
zgłoszeń oczekuje w kolejce.
○
Graf stanów systemu
μ
. . .
μ
μ
μ
μ
S
2
S
1
S
0
. . .
μ
μ
S
k+1
S
k
S
k-1
λ
λ
λ
λ
λ
λ
λ
STANY
BEZ KOLEJKI
STANY
Z KOLEJKĄ
Rys. 1. Graf stanów
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
5
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
○
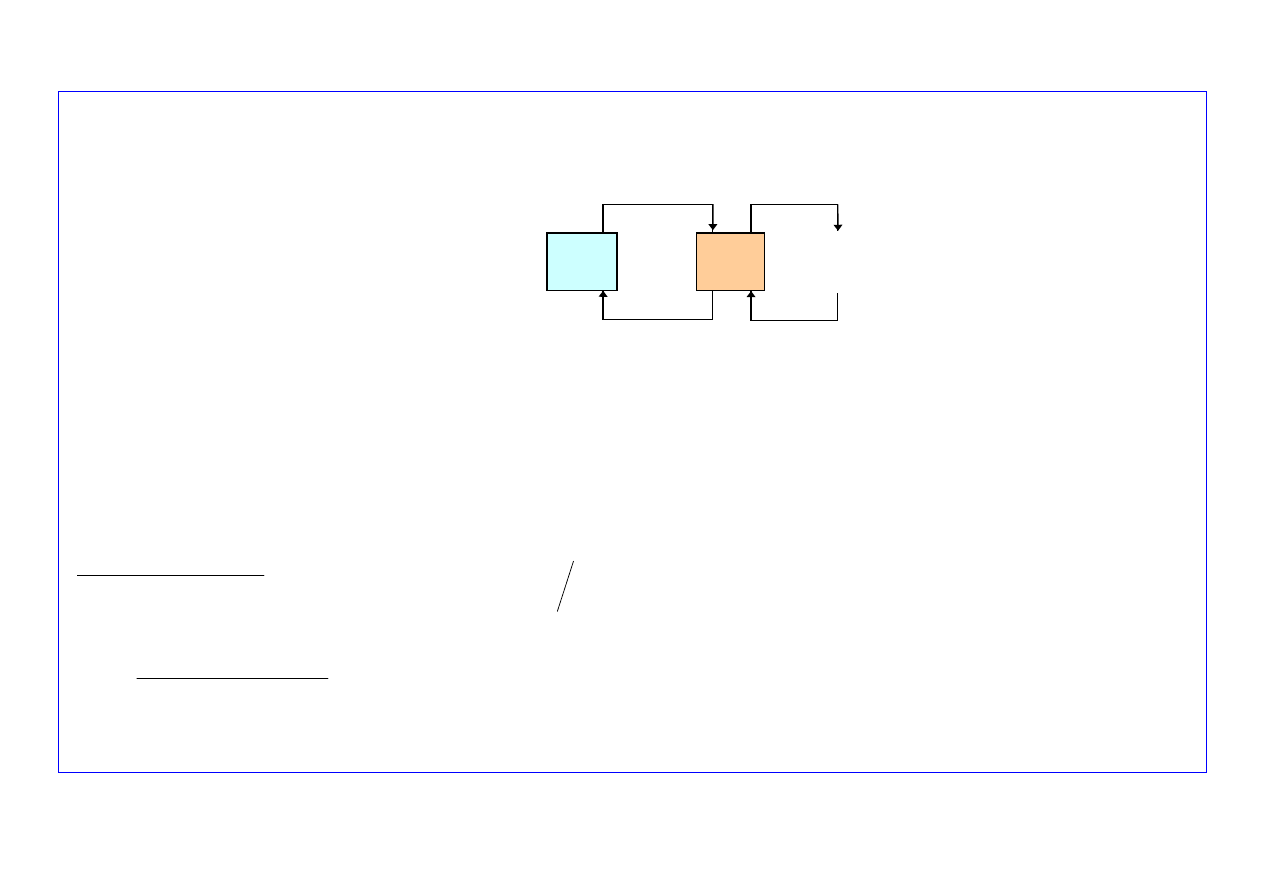
Stacjonarne prawdopodobieństwa stanów systemu
1.
μ
λ
. . .
λ
μ
S
0
S
1
(
)
( ) (
)
( )
( )
t
o
t
t
p
t
t
p
t
t
p
Δ
+
Δ
⋅
⋅
+
Δ
⋅
−
⋅
=
Δ
+
μ
λ
1
0
0
1
gdzie: o(
Δ
t)
− prawdopodobieństwo, że w przedziale
Δ
t nastąpi co najmniej dwukrotna zmiana stanu
systemu; jest bardzo małe i dalej będzie pomijane.
(
)
( )
( )
( )
μ
λ
⋅
+
⋅
−
=
Δ
−
Δ
+
t
p
t
p
t
t
p
t
t
p
1
0
0
0
lim
0
→
Δt
(
)
( )
( )
( )
μ
λ
⋅
+
⋅
−
=
Δ
−
Δ
+
→
Δ
t
p
t
p
t
t
p
t
t
p
t
1
0
0
0
0
lim
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
6
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
Wykorzystując definicję pochodnej
( )
(
)
( )
t
t
p
t
t
p
dt
t
dp
t
Δ
−
Δ
+
=
→
Δ
0
0
0
0
lim
otrzymuje się
( )
( )
( )
μ
λ
⋅
+
⋅
−
=
t
p
t
p
dt
t
dp
1
0
0
Dla warunków ustalonych:
( )
0
0
=
dt
t
dp
;
( )
0
0
p
t
p
=
;
( )
1
1
p
t
p
=
;
stąd
μ
λ
⋅
+
⋅
−
=
1
0
0
p
p
oraz
μ
λ
⋅
=
0
1
p
p
, a gdy przyjmie się, że
μ
λ
ρ
= , to
ρ
⋅
=
0
1
p
p
(1)
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
7
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
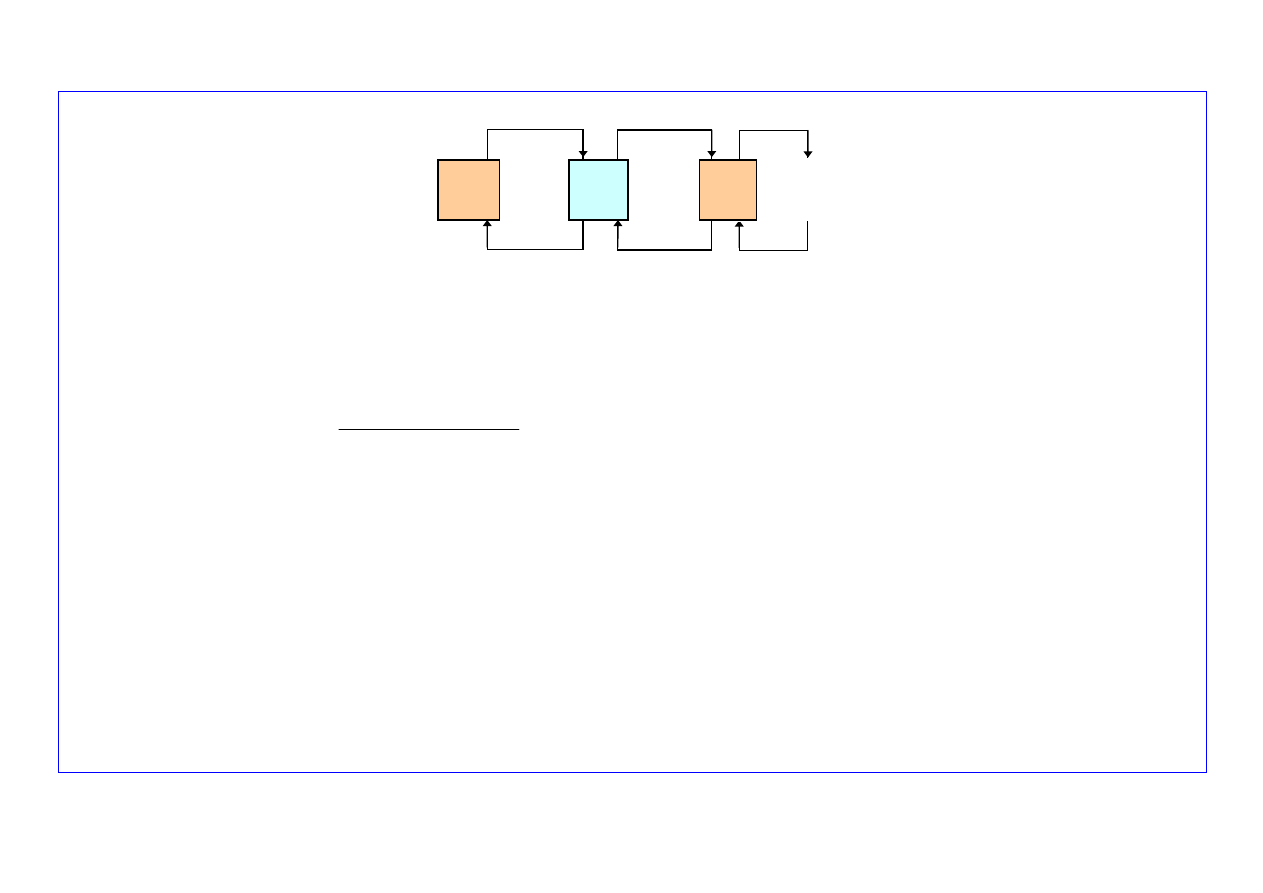
2.
μ
. . .
λ
λ
μ
μ
S
0
S
1
S
2
λ
(
)
( )
(
)
[
]
( )
( )
t
t
p
t
t
p
t
t
p
t
t
p
Δ
⋅
⋅
+
Δ
⋅
⋅
+
Δ
⋅
+
−
⋅
=
Δ
+
μ
λ
μ
λ
2
0
1
1
1
(
)
( )
( ) (
)
( )
( )
μ
λ
μ
λ
⋅
+
⋅
+
+
⋅
−
=
Δ
−
Δ
+
t
p
t
p
t
p
t
t
p
t
t
p
2
0
1
1
1
Dla warunków ustalonych:
(
)
μ
λ
μ
λ
⋅
+
⋅
+
+
⋅
−
=
2
0
1
0
p
p
p
Wykorzystując równanie (1)
(
)
μ
λ
μ
λ
ρ
⋅
+
⋅
+
+
⋅
⋅
−
=
2
0
0
0
p
p
p
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
8
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
Stąd
(
)
μ
λ
μ
λ
ρ
μ
⋅
−
+
⋅
⋅
⋅
=
0
0
2
1
p
p
p
a gdy
μ
λ
ρ
=
mamy
⎥
⎦
⎤
⎢
⎣
⎡
−
+
⋅
⋅
=
1
0
2
μ
μ
λ
ρ
p
p
a dalej
⎥
⎦
⎤
⎢
⎣
⎡
−
+
⋅
⋅
=
1
1
0
2
μ
λ
ρ
p
p
Stąd zależność na prawdopodobieństwo stacjonarne
przedstawia zależność
:
2
p
2
0
2
ρ
⋅
= p
p
(2)
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
9
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
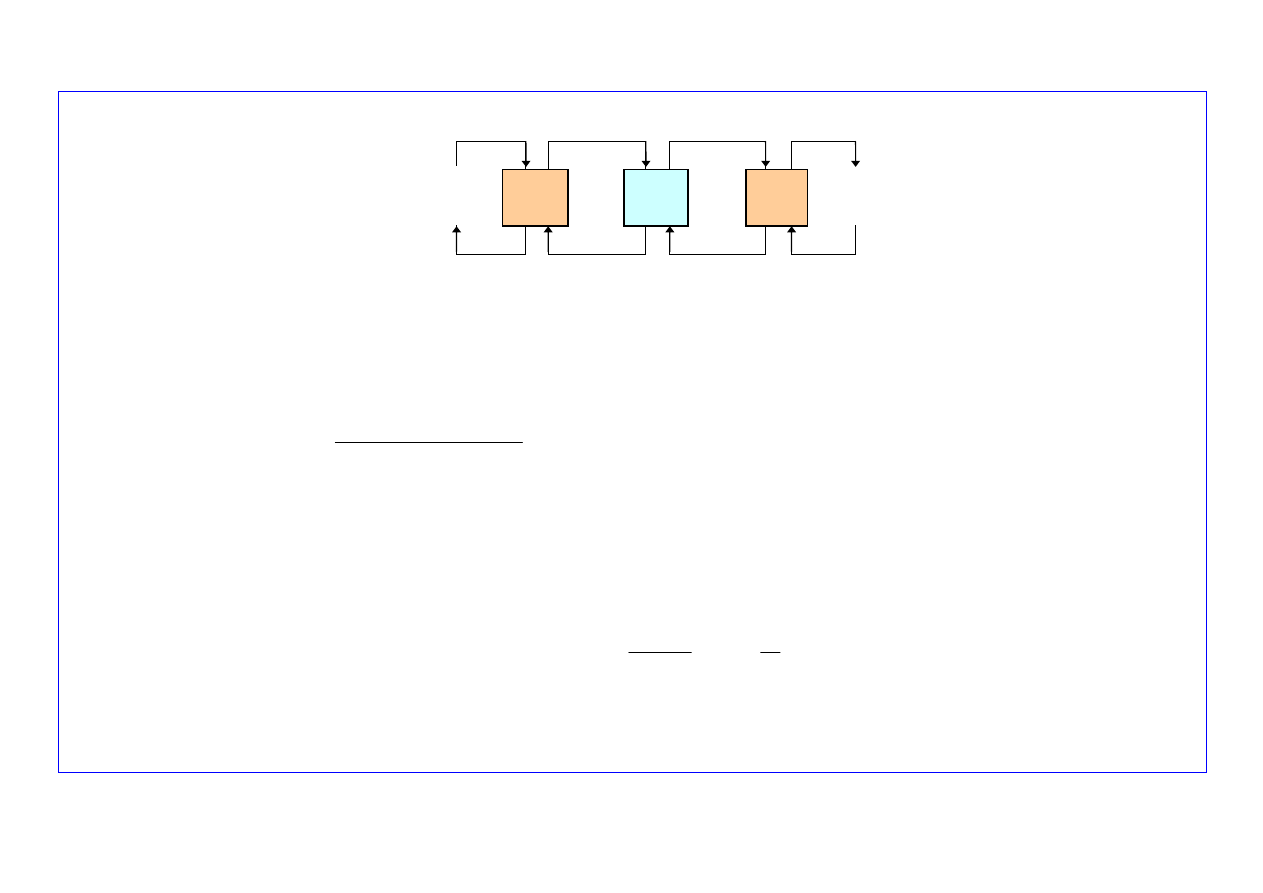
3.
μ
μ
. . .
λ
λ
λ
λ
μ
μ
S
1
S
2
S
3
. . .
(
)
( )
(
)
[
]
( )
( )
t
t
p
t
t
p
t
t
p
t
t
p
Δ
⋅
⋅
+
Δ
⋅
⋅
+
Δ
⋅
+
−
⋅
=
Δ
+
μ
λ
μ
λ
3
1
2
2
1
(
)
( )
( ) (
)
( )
( )
μ
λ
μ
λ
⋅
+
⋅
+
+
⋅
−
=
Δ
−
Δ
+
t
p
t
p
t
p
t
t
p
t
t
p
3
1
2
2
2
Dla warunków ustalonych:
(
)
μ
λ
μ
λ
⋅
+
⋅
+
+
⋅
−
=
3
1
2
0
p
p
p
stąd:
μ
λ
μ
μ
λ
⋅
−
+
⋅
=
1
2
3
p
p
p
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
10
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
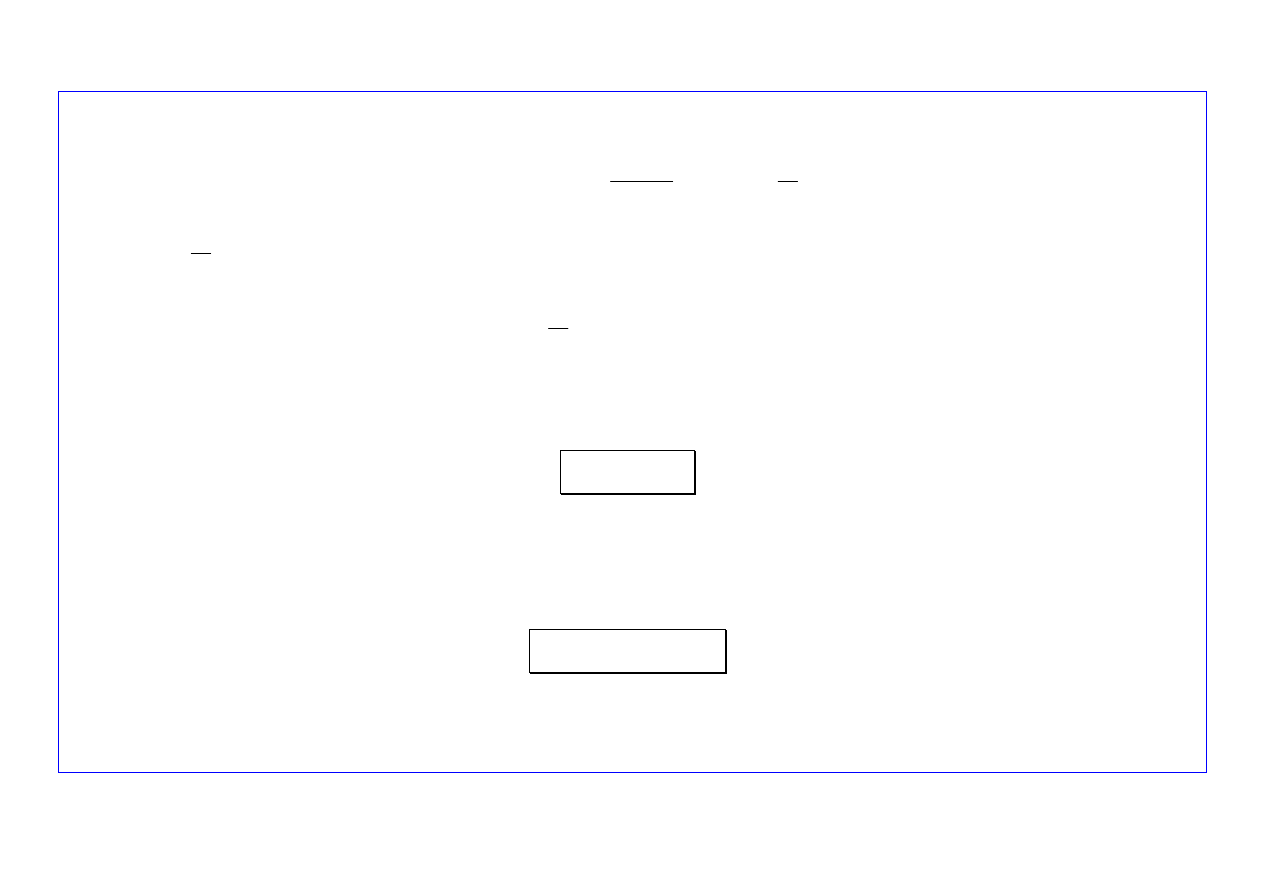
Wykorzystując równania
(1)
i
(2)
μ
λ
ρ
μ
μ
λ
ρ
⋅
⋅
−
+
⋅
⋅
=
0
2
0
3
p
p
p
,
a gdy
μ
λ
ρ
= , mamy:
(
)
1
1
1
1
2
0
2
0
3
−
+
⋅
⋅
=
⎟
⎠
⎞
⎜
⎝
⎛
−
+
⋅
⋅
=
ρ
ρ
μ
λ
ρ
p
p
p
Stąd zależność na prawdopodobieństwo stacjonarne
przedstawia zależność:
3
p
3
0
3
ρ
⋅
= p
p
(3)
Na podstawie zależności (1),(2) i (3), można zauważyć, że obowiązuje zależność rekurencyjna:
ρ
⋅
=
+
k
k
p
p
1
a stąd
ρ
ρ
⋅
⋅
=
+
k
k
p
p
0
1
(4)
i
1
0
1
+
+
⋅
=
k
k
p
p
ρ
(5)
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
11
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
Porządkując wykonane obliczenia można zapisać, że:
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
⋅
=
⋅
=
⋅
=
⋅
=
⋅
=
⋅
=
+
+
−
−
M
M
1
0
1
0
1
0
1
3
0
3
2
0
2
0
1
k
k
k
k
k
k
p
p
p
p
p
p
p
p
p
p
p
p
ρ
ρ
ρ
ρ
ρ
ρ
(6)
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
12
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
Oczywiście obowiązuje tu również warunek, że:
1
0
=
∑
∞
=
i
i
p
(7)
Wykorzystując równania (6) i (7) można zapisać, że:
1
0
2
0
0
0
=
+
⋅
+
+
⋅
+
⋅
+
L
L
k
p
p
p
p
ρ
ρ
ρ
a stąd
(
)
1
geometr.
ciagu
nieskoncz.
suma
1
2
0
0
1
−
−
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
+
+
+
+
=
4
4
4
3
4
4
4
2
1
K
K
q
a
k
p
ρ
ρ
ρ
gdzie: a
0
− pierwszy wyraz nieskończonego ciągu geometrycznego,
q
− iloraz nieskończonego ciągu geometrycznego.
Dalej można więc zapisać, że:
1
1
0
1
1
1
1
−
−
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
+
=
ρ
ρ
ρ
p
co daje ostatecznie zależność postaci:
ρ
−
= 1
0
p
(8)
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
13
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
Wykorzystując równania
(6)
i
(8)
można napisać równania
(9)
wyrażające prawdopodobieństwa
stacjonarne stanów systemu M/M/1/
∞ postaci:
(
)
(
)
(
)
(
)
(
)
(
)
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
⋅
−
=
⋅
−
=
⋅
−
=
⋅
−
=
⋅
−
=
⋅
−
=
+
+
−
−
M
M
1
1
1
1
3
3
2
2
1
1
1
1
1
1
1
k
k
k
k
k
k
p
p
p
p
p
p
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
(9)
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
14
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
○
Średnia liczba zgłoszeń w systemie M/M/1/
∞
Korzystając z zależności na wartość oczekiwaną zmiennej losowej typu dyskretnego, średnią
liczbę zgłoszeń w systemie można obliczyć wg formuły:
∑
∞
=
⋅
=
0
sys
i
i
p
i
L
Rozpiszmy powyższą formułę bardziej szczegółowo do postaci:
(
)
{
(
)
{
(
)
{
K
K
+
⋅
+
+
⋅
+
⋅
+
⋅
=
−
⋅
−
⋅
−
⋅
ρ
ρ
ρ
ρ
ρ
ρ
1
1
2
1
1
0
sys
2
2
1
0
k
k
p
k
p
p
p
L
oraz uwzględnijmy zależność (9):
(
)
(
)
(
)
L
L
1
1
2
1
1
2
sys
+
−
⋅
⋅
+
+
−
⋅
⋅
+
−
⋅
⋅
=
ρ
ρ
ρ
ρ
ρ
ρ
k
k
L
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
15
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
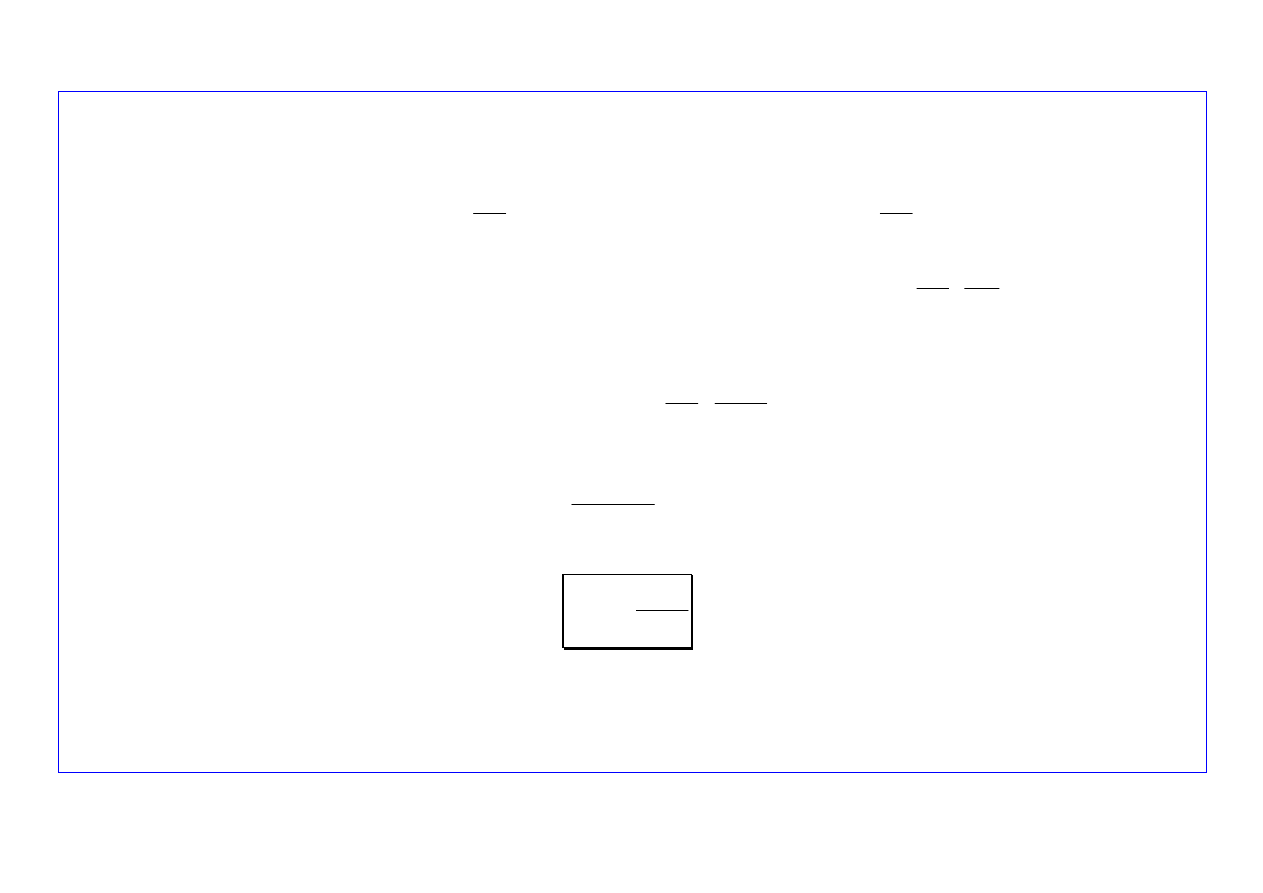
Można zauważyć, że powyższą zależność można zapisać w postaci:
(
)
i
i
d
d
L
ρ
ρ
ρ
ρ
1
1
sys
∑
∞
=
⋅
−
⋅
=
lub
(
)
3
2
1
ρ
ρ
ρ
ρ
ρ
ρ
−
=
−
∞
=
∑
⋅
−
⋅
=
1
1
1
sys
0
1
q
a
i
i
d
d
L
co prowadzi w efekcie końcowym do zależności (10):
⎟
⎠
⎞
⎜
⎝
⎛
−
⋅
−
⋅
=
ρ
ρ
ρ
ρ
ρ
1
)
1
(
sys
d
d
L
po obliczeniu pochodnej:
(
)
(
)
2
sys
1
1
1
ρ
ρ
ρ
−
⋅
−
⋅
=
L
ρ
ρ
−
=
1
sys
L
(10)
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
16
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
○
Średnia liczba zgłoszeń oczekujących w kolejce systemu M/M/1/
∞
Średnia liczba zgłoszeń w kolejce zostanie obliczona jako różnica średniej liczby zgłoszeń w
systemie i średniej liczby zgłoszeń obsługiwanych, wg zależności:
obs
sys
oczek
L
L
L
−
=
(11)
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
17
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
○
Średnia liczba zgłoszeń obsługiwanych w systemie M/M/1/
∞
Korzystając z zależności na wartość oczekiwaną zmiennej losowej typu dyskretnego, średnią
liczbę zgłoszeń obsługiwanych w systemie dysponującym jednym kanałem obsługowym, można
obliczyć wg formuły:
∑
=
⋅
=
1
0
obs
obs
i
i
p
i
L
Po rozpisaniu powyższej zależności otrzymuje się:
obs
obs
1
0
obs
1
0
p
p
L
⋅
+
⋅
=
ale
∑
∞
=
=
1
1
obs
k
k
p
p
co skutkuje w następującym zapisie:
(
)
3
2
1
ρ
ρ
ρ
-
1
-
1
nego
geometrycz
ciagu
nego
nieskonczo
suma
1
0
obs
obs
0
⋅
∞
=
∑
+
⋅
=
k
k
p
p
L
i zależnością końcową (12)
ρ
=
obs.
L
(12)
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
18
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞
○
Średnia liczba zgłoszeń oczekujących w kolejce systemu M/M/1/
∞ cd.
Teraz można powrócić do wyznaczenia średniej liczby zgłoszeń oczekujących w kolejce. Korzysta
się przy tym z zależności (10), (11) i (12):
{
ρ
ρ
ρ
ρ
ρ
ρ
ρ
−
+
−
=
−
−
=
1
1
2
(12)
zal.
(10)
zal.
oczek
3
2
1
L
otrzymując w końcu formułę (13) postaci:
ρ
ρ
−
=
1
2
oczek.
L
(13)
Plik:
BO_M_M_1_oo_Analityczne_p_s_[v3].doc
19
/
19
A. KADZIŃSKI,
ANALITYCZNE MODELE ELEMENTARNEGO SYSTEMU MASOWEJ OBSŁUGI M/M/1/∞