LABORATORIUM MECHANIKI EKSPERYMENTALNEJ
Instrukcja do ćwiczenia
1b
Wyznaczanie momentów bezwładności elementów
maszyn metodą wahadła fizycznego
Cel
ć
wiczenia
Celem
ć
wiczenia jest zapoznanie z eksperymentalnymi i analitycznymi metodami wy-
znaczania momentów bezwładno
ś
ci cz
ęś
ci maszyn. W ramach realizowanego
ć
wi-
czenia stosuje si
ę
metod
ę
wahadła fizycznego.
.
Literatura
1.
J.Leyko, Mechanika Ogólna, tom II, rozdz. VII.
2.
K.Zarankiewicz, Mechanika Teoretyczna, tom III, rozdz. X.
Zagadnienia kontrolne
1. Definicje momentów bezwładno
ś
ci ciała sztywnego:
a) wzgl
ę
dem płaszczyzny,
b) wzgl
ę
dem osi,
c) wzgl
ę
dem punktu.
2. Umiej
ę
tno
ść
wyznaczenia sposobem analitycznym momentów bezwładno
ś
ci pro-
stych ciał jednorodnych, jak: walec, kula, sto
ż
ek, sto
ż
ek
ś
ci
ę
ty itp.
3. Twierdzenie Steinera.
4. Analityczne wyznaczenie momentów bezwładno
ś
ci ciała zło
ż
onego z prostych ele-
mentów.
Uwaga. Instrukcja dotyczy podstaw samego
ć
wiczenia. Aby opanowa
ć
materiał
dotycz
ą
cy powy
ż
szych zagadnie
ń
nale
ż
y si
ę
gn
ąć
do podanej literatury.
Podstawy teoretyczne dotycz
ą
ce przeprowadzenia eksperymentu
Wahadłem fizycznym nazywamy dowolne ciało sztywne mog
ą
ce si
ę
obraca
ć
wo-
kół osi poziomej, które wykonuje drgania pod wpływem siły grawitacji (rysunek 1).
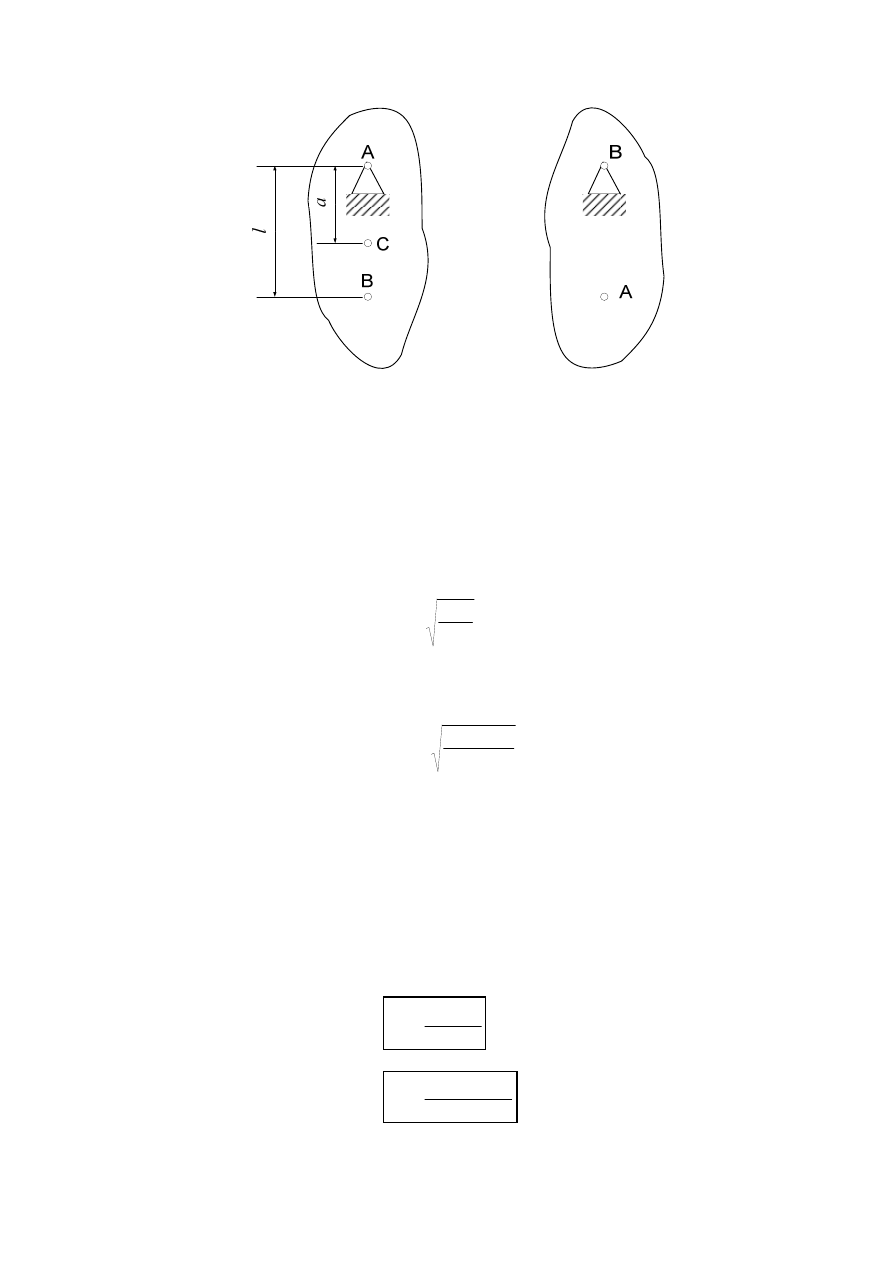
Rys. 1. Przekrój wahadła fizycznego i punkty zawieszenia A i B
Na rysunku 1 przedstawiono przekrój takiego ciała w płaszczy
ź
nie prostopadłej do
osi obrotu i przechodz
ą
cej przez
ś
rodek masy ciała. Wybrany punkt, w którym o
ś
ob-
rotu przebija wspomnian
ą
płaszczyzn
ę
, mo
ż
emy nazwa
ć
punktem zawieszenia wa-
hadła (na rysunku punkt A lub B w zale
ż
no
ś
ci od sposobu zawieszenia wahadła).
Mamy wyznaczy
ć
moment bezwładno
ś
ci wahadła wzgl
ę
dem osi przechodz
ą
cej
przez
ś
rodek masy C i równoległej do osi obrotu przechodz
ą
cej przez punkt A.
Okres drga
ń
wahadła fizycznego wynosi odpowiednio:
- gdy o
ś
obrotu przechodzi przez punkt A:
mag
J
T
A
A
π
2
=
,
(1a)
- gdy o
ś
obrotu przechodzi przez punkt B:
g
a
l
m
J
T
B
B
)
(
2
−
=
π
,
(1b)
gdzie: J
A
–moment bezwładno
ś
ci wahadła wzgl
ę
dem osi przechodz
ą
cej przez
punkt A,
J
B
–moment bezwładno
ś
ci wahadła wzgl
ę
dem osi przechodz
ą
cej przez punkt B,
a
– odległo
ść
punktu A od
ś
rodka masy C,
l
– odległo
ść
pomi
ę
dzy punktami A i B,
m – masa wahadła.
St
ą
d, momenty bezwładno
ś
ci wzgl
ę
dem osi przechodz
ą
cych odpowiednio
przez punkty A i B wynosz
ą
:
2
2
4
π
A
A
mgaT
J
=
]
[
2
m
kg
⋅
(2a)
(
)
2
2
4
π
B
B
T
a
l
mg
J
−
=
]
[
2
m
kg
⋅
(2b)
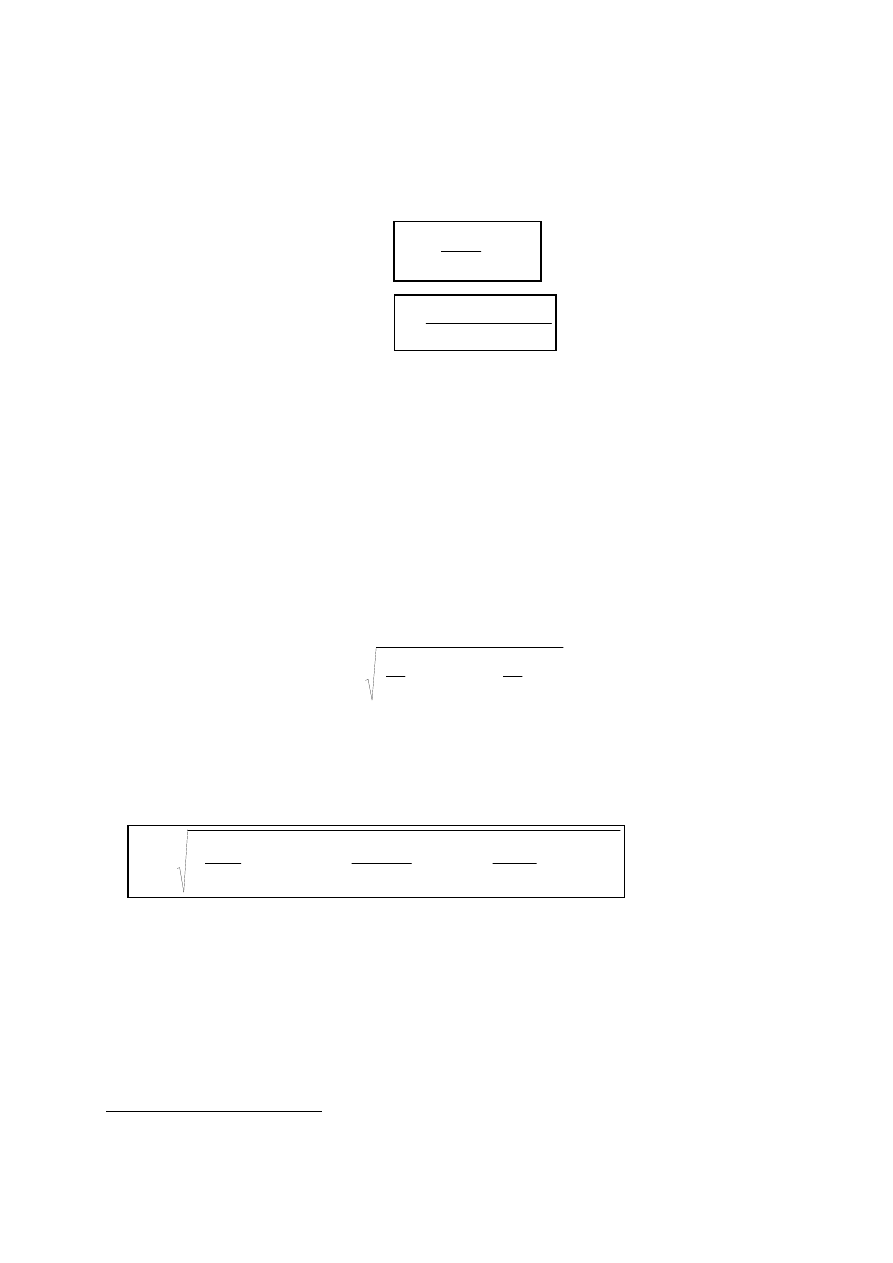
Korzystaj
ą
c z twierdzenia Steinera i z zale
ż
no
ś
ci (2a i 2b) mo
ż
na okre
ś
li
ć
mo-
ment bezwładno
ś
ci badanego elementu wzgl
ę
dem osi przechodz
ą
cej przez
ś
rodek
masy oraz odległo
ść
punktu zawieszenia A od
ś
rodka masy:
m
a
agT
J
A
c
−
=
2
2
2
4
π
]
[
2
m
kg
⋅
(3)
]
[m
(4)
Oszacowanie niepewno
ś
ci pomiarowej
Załó
ż
my dalej,
ż
e niepewno
ś
ci poszczególnych pomiarów s
ą
niezale
ż
ne i losowe.
Aby upro
ś
ci
ć
obliczenia przyjmijmy,
ż
e niepewno
ść
oszacowania g (przyspieszenia
ziemskiego) jest pomijalnie mała (bliska zeru) w porównaniu do innych niepewno
ś
ci.
Dla uproszczenia przyjmijmy,
ż
e pomiar
a
obarczony jest niepewno
ś
ci
ą
:
(5)
Ogólna zale
ż
no
ść
okre
ś
laj
ą
ca jak si
ę
przenosz
ą
bł
ę
dy wielko
ś
ci mierzonych na
wyznaczan
ą
po
ś
rednio wielko
ść
, przy zało
ż
eniu niezale
ż
no
ś
ci bł
ę
dów wielko
ś
ci mie-
rzonych, przedstawia si
ę
nast
ę
puj
ą
co
1
:
2
2
...
∆
∂
∂
+
+
∆
∂
∂
=
∆
z
z
y
x
x
y
y
(6)
gdzie y(x,..z) jest wielko
ś
ci
ą
wyznaczan
ą
metod
ą
po
ś
redni
ą
na podstawie pomiaru
warto
ś
ci x,...z.
Ostatecznie mo
ż
na zapisa
ć
,
ż
e niepewno
ść
oszacowania momentu bezładno
ś
ci
elementu wzgl
ę
dem osi przechodz
ą
cej przez
ś
rodek ci
ęż
ko
ś
ci wynosi:
2
2
2
2
2
2
2
2
2
4
4
2
4
∆
−
+
∆
+
∆
−
=
∆
m
a
agT
T
agmT
a
m
a
gT
J
A
A
A
A
c
π
π
π
]
[
2
m
kg
⋅
(7)
Podobnie niepewno
ść
towarzysz
ą
c
ą
pomiarowi metod
ą
po
ś
redni
ą
momentu bez-
władno
ś
ci elementu wzgl
ę
dem osi przechodz
ą
cej przez punkt A i punkt B mo
ż
na
oszacowa
ć
jako:
1
Aby poszerzyć wiedze z tego zakresu sięgnij po książkę: John R. Taylor; Wstęp do analizy błędu pomiarowego;
PWN Warszawa 1999 i późniejsze wydania (rozdział 3).
(
)
l
T
T
g
l
glT
a
B
A
B
2
2
2
2
2
2
8
4
π
π
−
+
−
=
l
a
∆
≈
∆
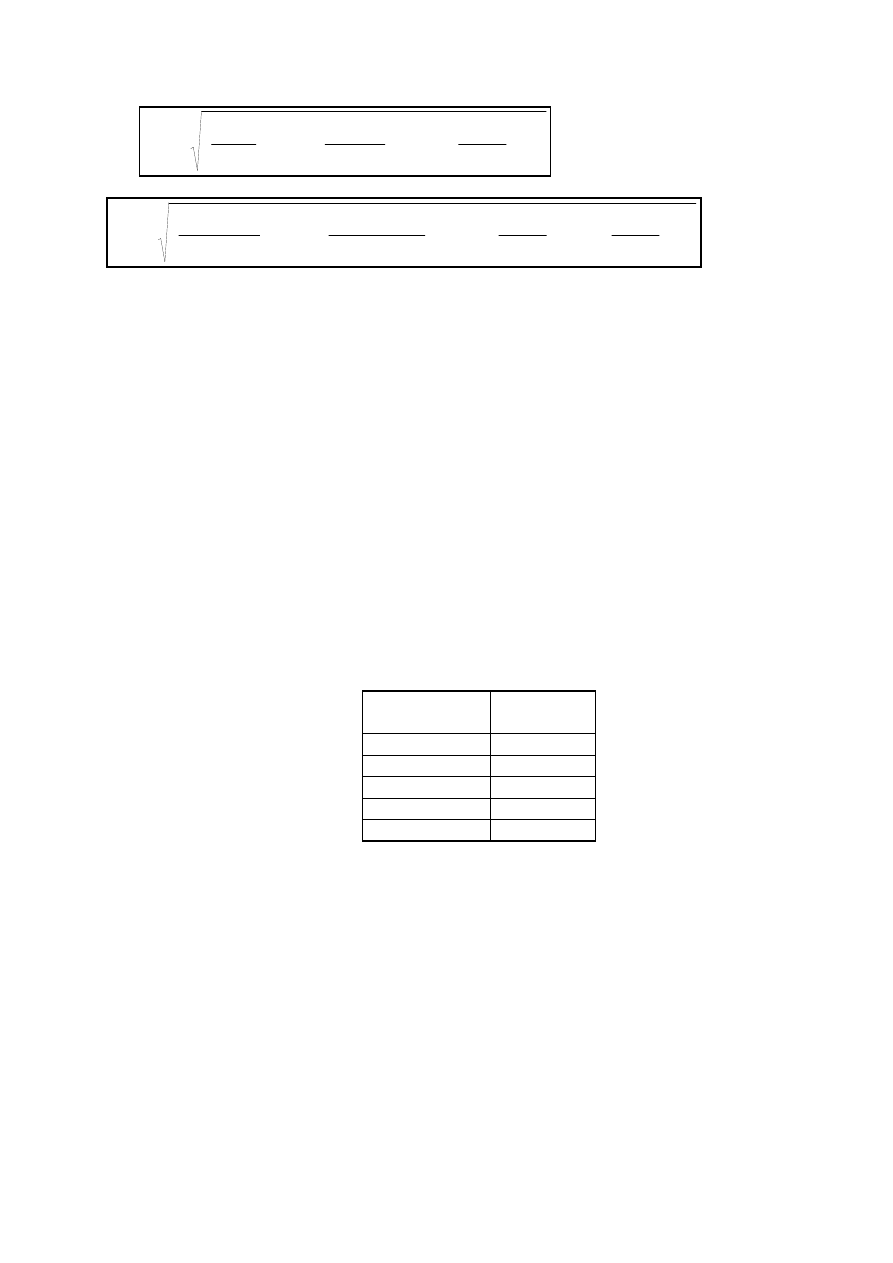
2
2
2
2
2
2
2
2
4
4
2
4
∆
+
∆
+
∆
=
∆
a
mgT
T
mgaT
m
gaT
J
A
A
A
A
A
π
π
π
]
[
2
m
kg
⋅
(8)
2
2
2
2
2
2
2
2
2
2
2
4
4
4
)
(
2
4
)
(
∆
+
∆
+
∆
−
+
∆
−
=
∆
l
mgT
a
mgT
T
T
a
l
mg
m
T
a
l
g
J
B
B
B
B
B
B
π
π
π
π
]
[
2
m
kg
⋅
gdzie:
l
T
T
B
A
∆
∆
∆
,
,
s
ą
niepewno
ś
ciami pomiarowymi wielko
ś
ci mierzonych bezpo-
ś
rednio: okresów waha
ń
wahadła podwieszonego na osiach przechodz
ą
cych przez
punkty A i B oraz odległo
ś
ci pomi
ę
dzy A i B.
Przebieg
ć
wiczenia
Opis kolejnych kroków, które nale
ż
y wykona
ć
znajduje si
ę
w arkuszu sprawozdania.
Poni
ż
ej zwrócono uwag
ę
na pewne istotne zagadnienia.
•
Nale
ż
y zmierzy
ć
czas co najmniej 10 wahni
ęć
elementu dla dwóch ró
ż
nych
podwiesze
ń
elementu
•
Ka
ż
dy pomiar nale
ż
y powtórzy
ć
20 razy.
•
G
ę
sto
ś
ci materiałów niezb
ę
dne do analitycznych oblicze
ń
momentu bezwład-
no
ś
ci podane s
ą
w zamieszczonej ni
ż
ej tabeli.
•
We wnioskach nale
ż
y si
ę
ustosunkowa
ć
do otrzymanych wyników, a w szcze-
gólno
ś
ci ró
ż
nic pomi
ę
dzy warto
ś
ciami uzyskanymi z oblicze
ń
analitycznych
oraz z eksperymentu, uwzgl
ę
dniaj
ą
c przy tym oszacowanie niepewno
ś
ci po-
miarowej.
Materiał
G
ę
sto
ść
[kg/m
3
]
Mosi
ą
dz
8500
Stal
7800
Bakelit
1100-1600
Ebonit
1400-1800
Duraluminium
2750