Optyka geometryczna

Podstawowe pojęcia optyki geometrycznej

Bezwzględny współczynnik załamania

v

c

n

=

c

– prędkość światła w próżni

v < c

– prędkość światła w danym ośrodku

> 1

Aksjomaty

Światło w ośrodku jednorodnym propaguje się

po liniach prostych nazywanych promieniami

świetlnymi

Aksjomaty

cd

n

b

< n

a

n

a

N

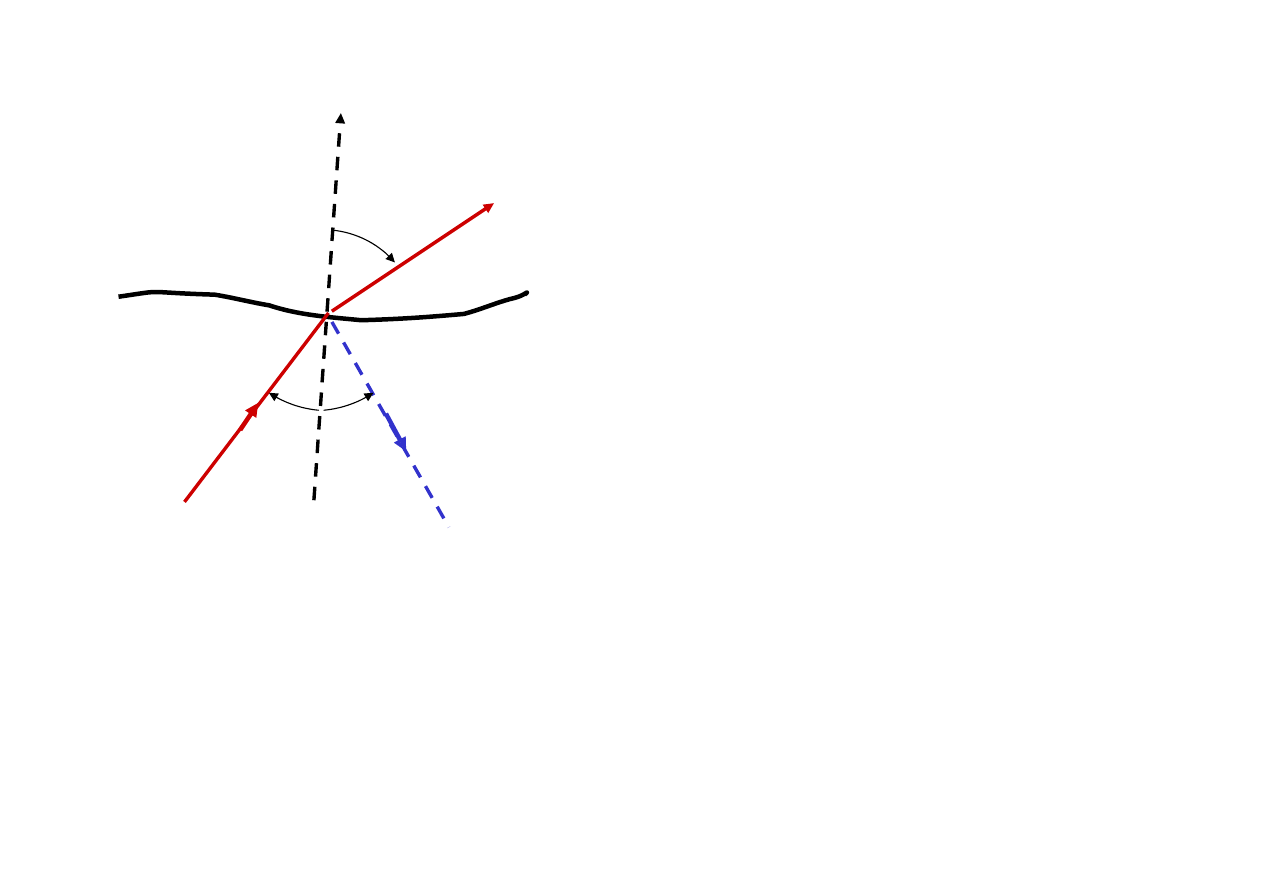
Prawo załamania

b

b

a

a

sin

n

sin

n

α

=

α

Promień padający, normalna

N

i promień załamany leżą w tej

samej płaszczyźnie

α

a

Promień

padający

α

b

Promień

załamany

Prawo odbicia

a

a

'

α

=

α

Promień padający, normalna

N

i promień odbity

leżą w tej samej płaszczyźnie

α’

a

Promień

odbity

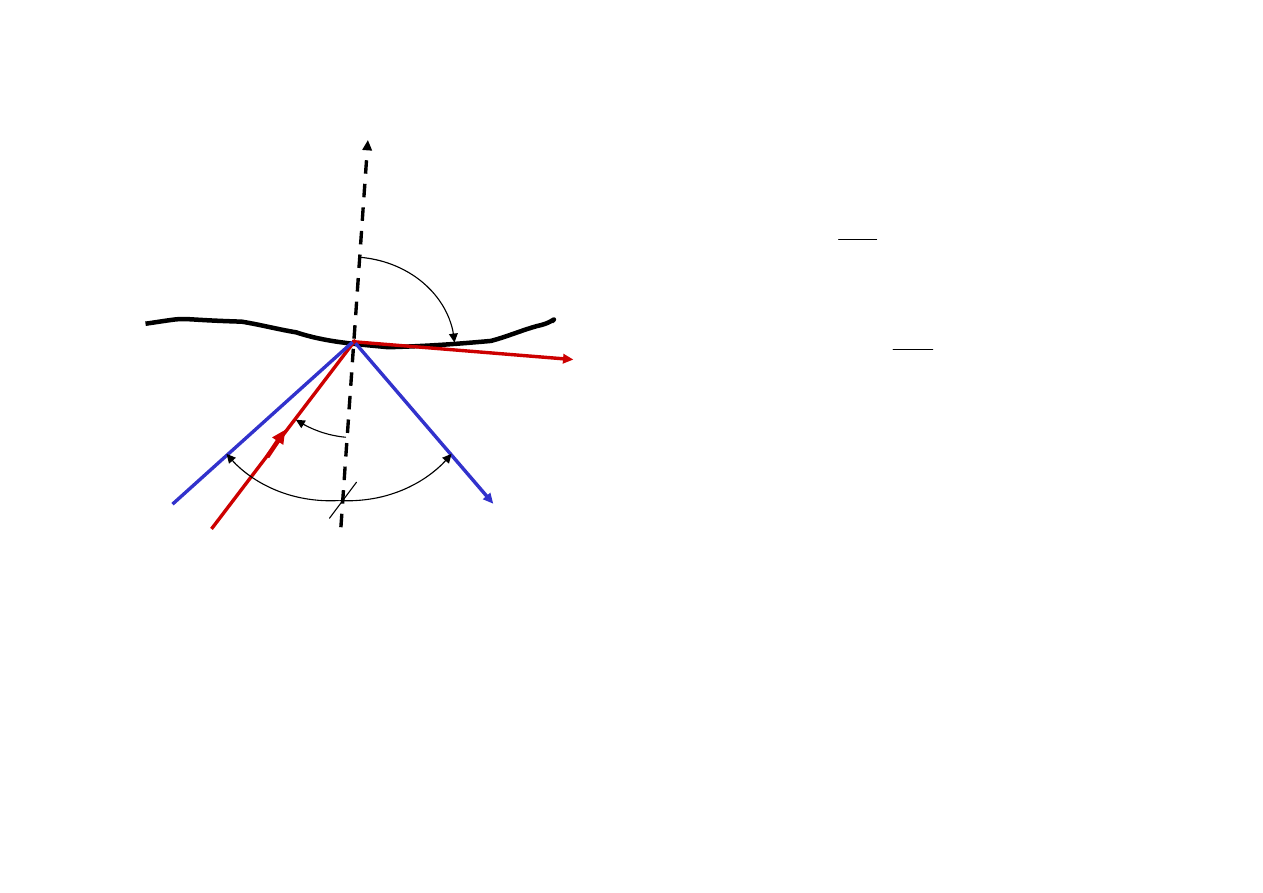
Całkowite wewnętrzne odbicie

n

b

< n

a

n

a

N

α

ag

Promienie

padające

α

bg

=

π/2

Promień

załamany
graniczny

α’

a

α

a

Ponieważ

n

a

> n

b

1

sin

n

n

sin

ag

b

a

bg

=

α

=

α

i

1

n

n

sin

a

b

ag

<

=

α

Dla promienia

α

a

>

α

ag

1

sin

b

>

α

Promień ulega

całkowitemu wewnętrznemu odbiciu

według prawa odbicia

a

a

'

α

=

α

Zastosowanie w światłowodach

Względny współczynnik załamania

Bezwzględny współczynnik załamania powietrza

760

p

273

/

t

1

a

1

n

+

+

≈

λ

0

[nm]

334 546 656 1530

a

[

⋅10

6

]

303 293 291 288

t

– temperatura w

0

C

p

–

ciśnienie w mm Hg

n

≈ 1.0003

Zmiana z temperaturą dla p = 760

t

10

n

6

Δ

−

≈

Δ

−

1

2

1

2

2

1

n

n

v

c

v

c

v

v

n

=

=

=

1

– ośrodek odniesienia

najczęściej powietrze

n

2

n

1

–

bezwzględne

współczynniki załamania

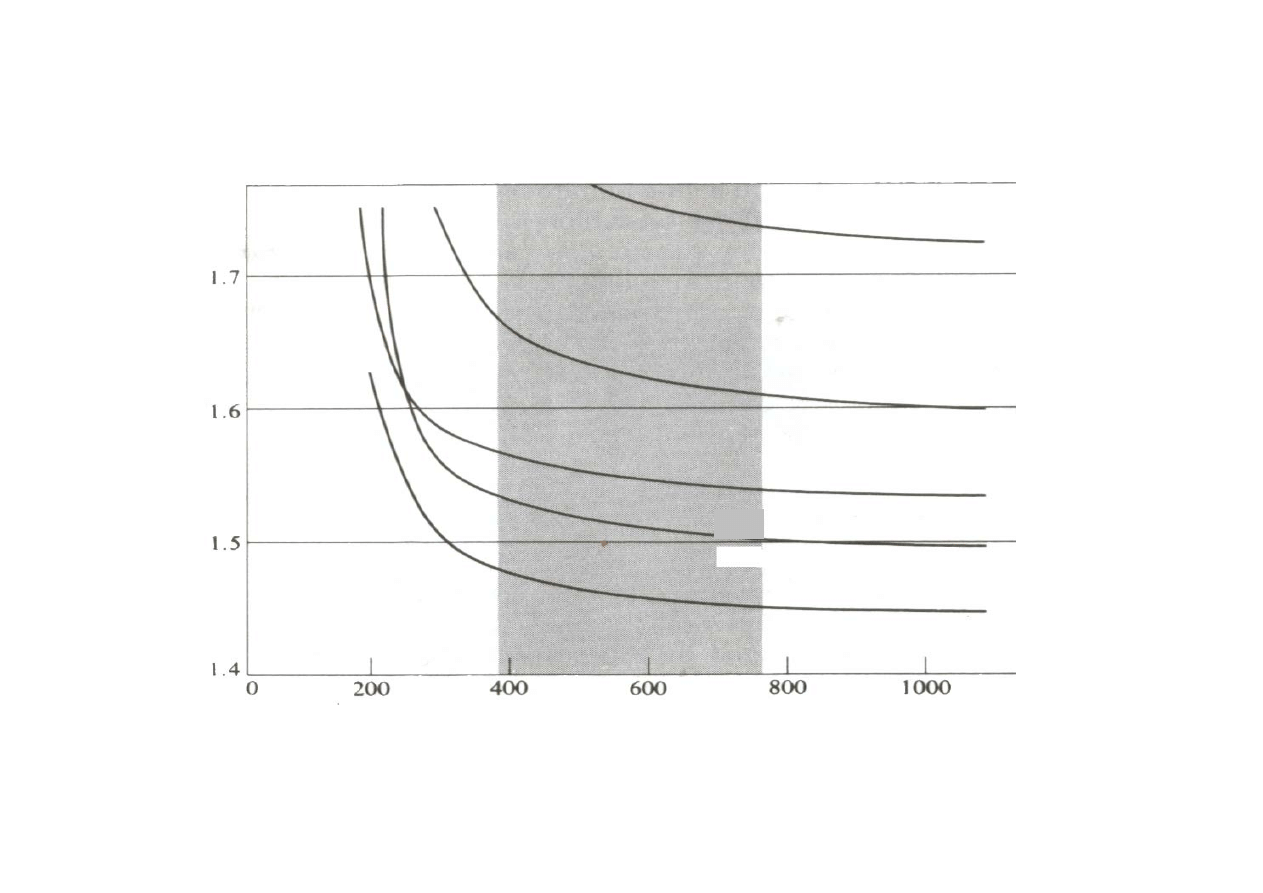
Właściwości dyspersyjne i absorpcyjne materiałów

Widmo słońca

linie (Josefa) Fraunhofera

i365

g435 F486 e546 d587 C656 t1014 nm

Hg Hg H Hg He H Hg

220 365 435.6 656.3 [nm] 1.014 5 [

μm]

Kwarc topiony

1.528 1.475 1.467 1.456 1.450 x

Sz. kronowe

x 1.539 1.526 1.514 1.507 x

Sz. flintowe

x 1.815 1.774 1.721 1.715 x

Krzem

x x x x

x 3.422

German

x x x x

x 4.017

KBr

1.853 1.606 1.583 1.555 1.544 1.534

UV n

i

n

g

n

C

n

t

IR

Wspó

łczynnik

za

łamania

Długość fali

λ

nm

Szkło kwarcowe

Kron

Kwarc

Lekki flint

Ci

ęż

ki flint

Krzywe dyspersyjne materiałów

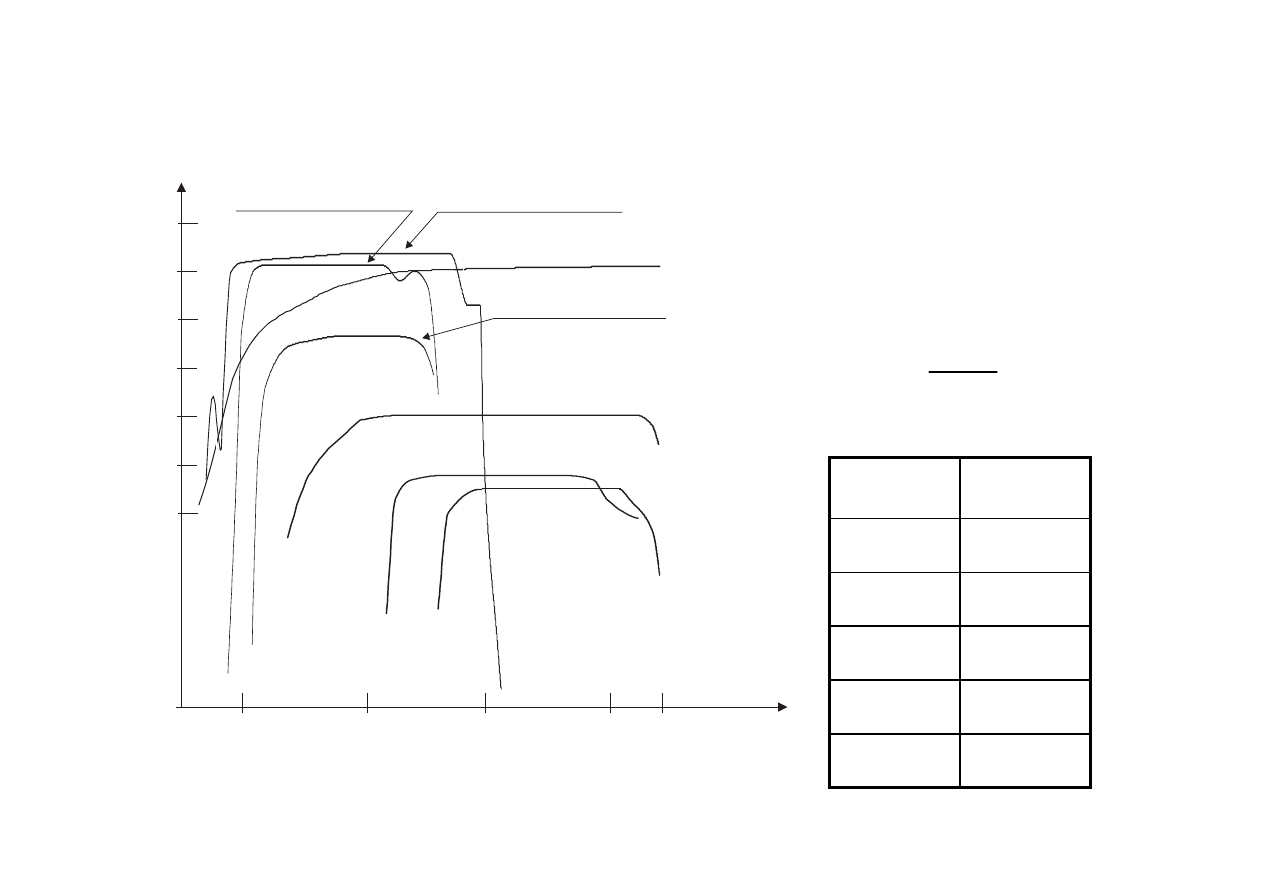
KBr

Ge

szk³o kronowe

szk³o flintowe

Si

ZnSe

Szk³o kwarcowe

1.0

0.3

1.0

3.0

10 16 l m

[ m]

0

0.4

0.5

0.9
0.8

T

Właściwości transmisyjne płytki

Współczynniki

odbicia powierzchni

materiał - powietrze

2

1

n

1

n

⎟

⎠

⎞

⎜

⎝

⎛

+

−

=

ρ

36.0

4.0

11.1

2.0

8.1

1.8

5.3

1.6

4.0

1.5

ρ[%]

n

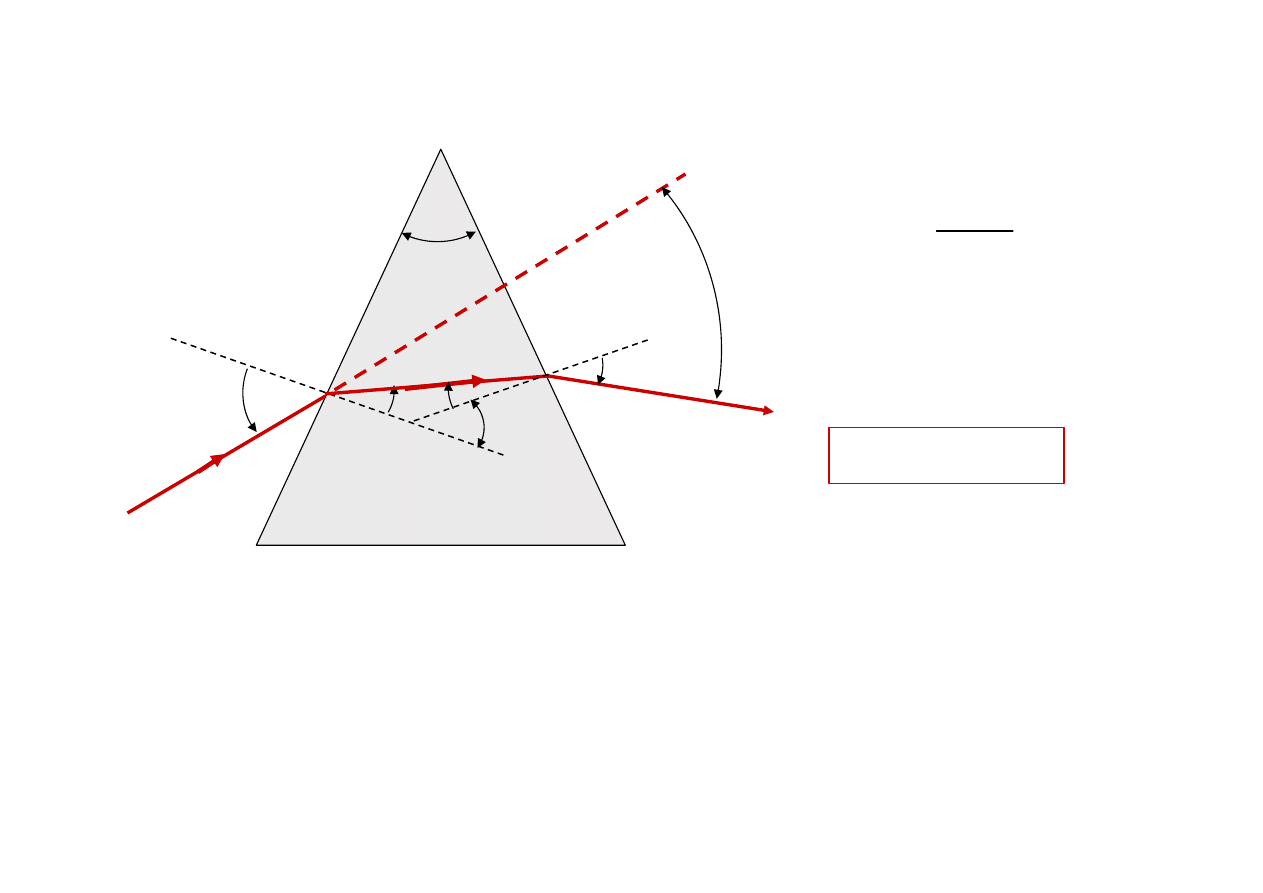
Pryzmat

Reguła znaków

ϕ

n = 1

n = 1

n

α’

2

δ

-

α

1

-

α’

1

n

sin

'

sin

1

1

α

=

α

α

2

ϕ

1

2

'

α

+

ϕ

=

α

2

2

sin

n

'

sin

α

=

α

ϕ

−

α

−

α

=

δ

1

2

'

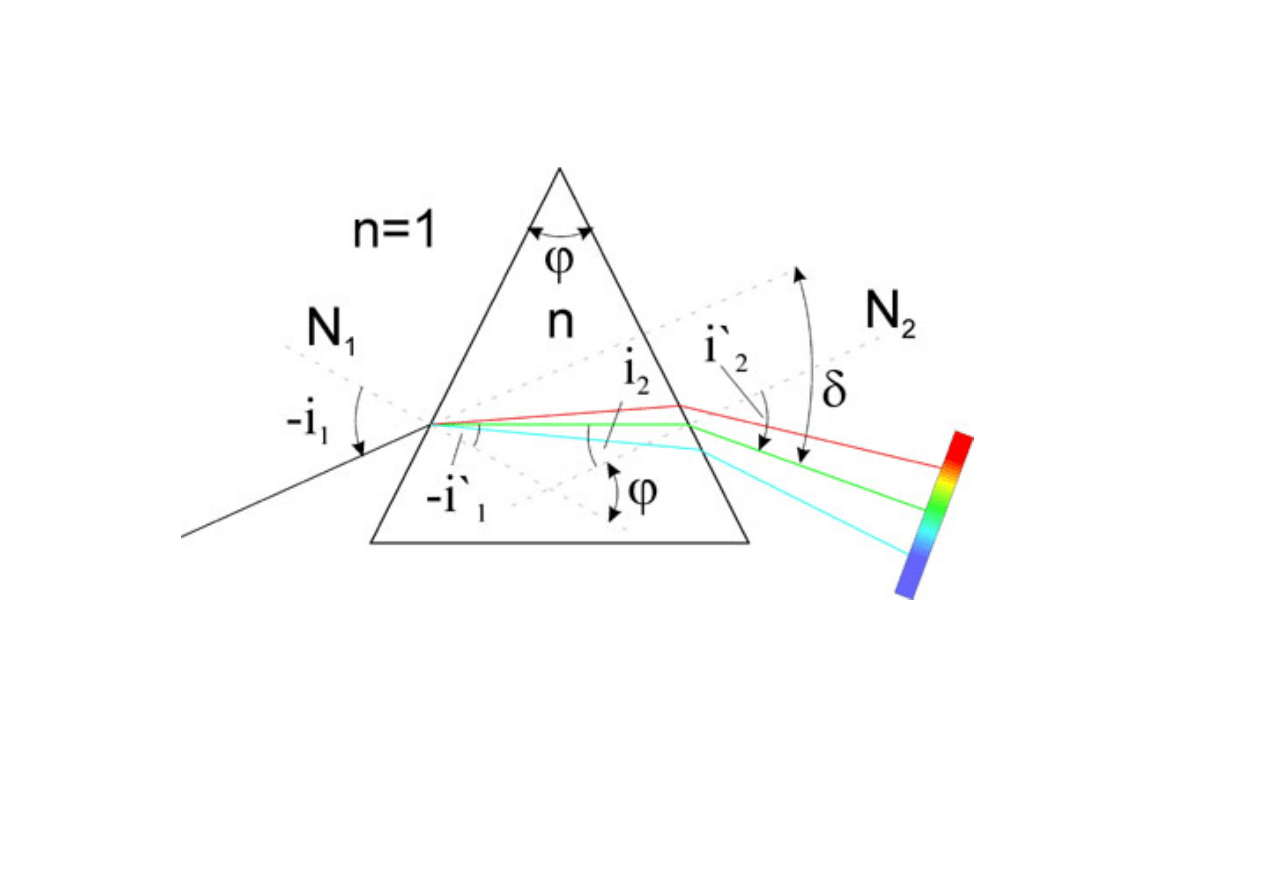
Pryzmat

( )

( )

ϕ

−

α

−

λ

α

=

λ

δ

1

2

'

Świ

atło

bia

łe

Tęcza.swf

Klin

– pryzmat o małym kącie łamiącym

ϕ

2

2

1

2

1

1

n

'

'

n

'

α

=

α

α

+

ϕ

=

α

α

=

α

ϕ

−

α

−

⎟

⎠

⎞

⎜

⎝

⎛

α

+

ϕ

=

ϕ

−

α

−

α

=

δ

1

1

1

2

n

n

'

(

)

1

n

−

ϕ

=

δ

i dla małego kąta padania

α

1

ϕ

δ

tęcza1b.swf

Układ optyczny

obszar o pewnym rozkładzie współczynnika załamania

Cel budowy

Zbiór powierzchni o skokowej zmianie

współczynnika załamania

Ograniczony obszar o ciągłej jego zmianie

układ gradientowy

Przykłady:

Przekształcenie przestrzeni przedmiotowej w obrazową w

celu zarejestrowania informacji o przedmiocie przez odbiornik

Optyka

Fotonika dodatkowo

Kształtowanie wiązki np. laserowej

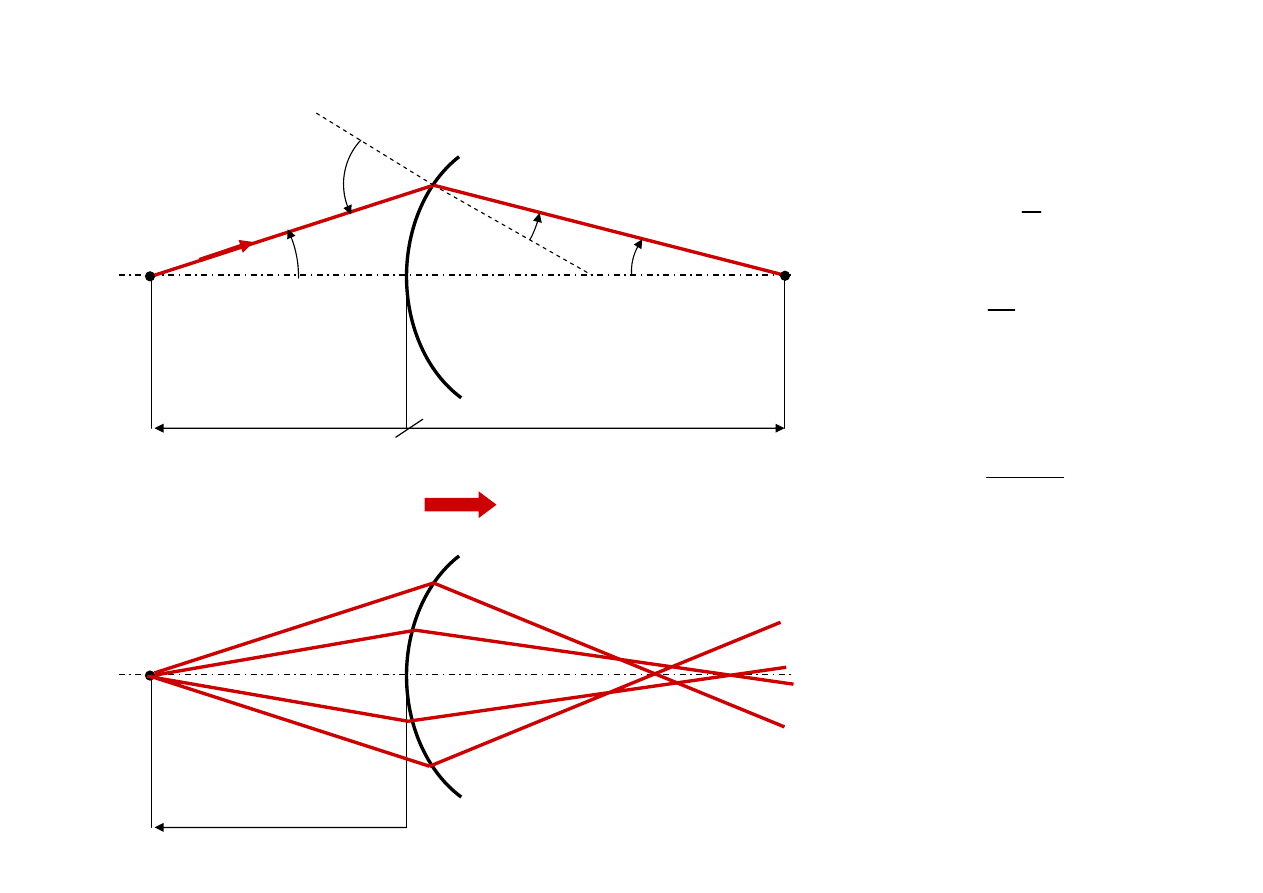
Powierzchnia sferyczna

układ elementarny

n

n’

O

r

P

-S

-u

-

α

u

sin

r

S

1

sin

⎟

⎠

⎞

⎜

⎝

⎛ −

=

α

P’

u’

-

α’

S’

α

=

α

sin

'

n

n

'

sin

α

−

α

+

=

'

u

'

u

⎟

⎠

⎞

⎜

⎝

⎛

α

−

=

'

u

sin

'

sin

1

r

'

S

Dane wejściowe

P

(S,u)

Dane wyjściowe

P’

(S’,u’)

P

-S

( )

u

'

S

'

S

=

Aberracja
sferyczna

pow_sfer.swf

Układ elementarny – przestrzeń przyosiowa

sinx

≈ x

=

−

s

n

'

s

'

n

r

n

'

n

s

n

'

s

'

n

−

=

−

u

sin

r

S

1

sin

⎟

⎠

⎞

⎜

⎝

⎛ −

=

α

α

=

α

sin

'

n

n

'

sin

α

−

α

+

=

'

u

'

u

⎟

⎠

⎞

⎜

⎝

⎛

α

−

=

'

u

sin

'

sin

1

r

'

S

u

r

s

1

⎟

⎠

⎞

⎜

⎝

⎛ −

=

α

α

=

α

'

n

n

'

α

−

α

+

=

'

u

'

u

⎟

⎠

⎞

⎜

⎝

⎛

α

−

=

'

u

'

1

r

'

s

S’

→ s’ S → s

(

) (

)

⎥⎦

⎤

⎢⎣

⎡

α

−

α

−

−

α

−

u

u

n

u

'

n

r

1

=

⎟

⎠

⎞

⎜

⎝

⎛

α

−

−

α

−

u

nu

'

'

u

'

u

'

n

r

1

W przestrzeni przyosiowej

s’

jest niezależne od małego

u

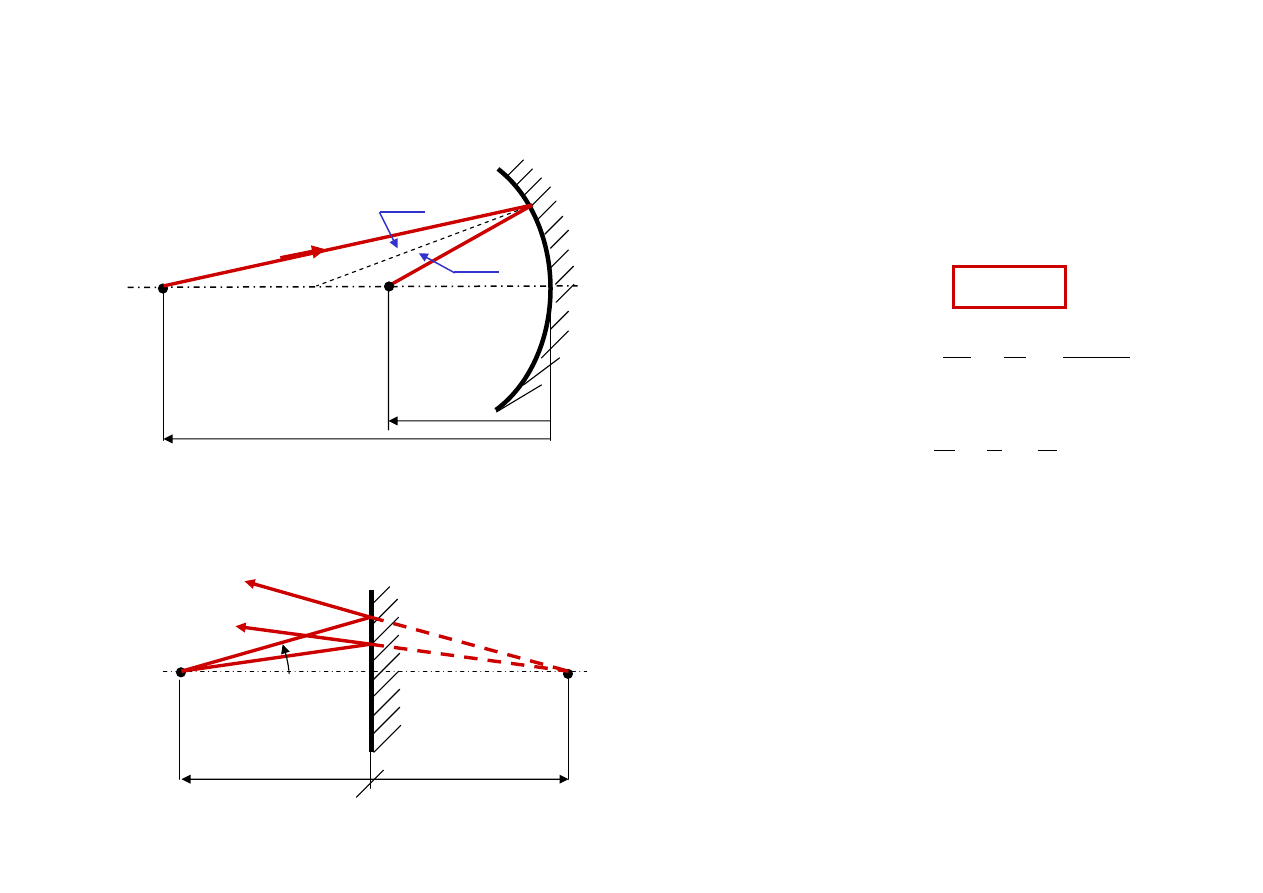
Zwierciadło w przestrzeni przyosiowej

P

-s

P’

-s’

α

-

α’

Zgodnie z regułą znaków

α’ = -α

co formalnie dla prawa załamania

α

=

α n

'

'

n

oznacza

n

'

n

−

=

r

n

'

n

s

n

'

s

'

n

−

=

−

Po podstawieniu do

r

2

s

1

'

s

1

=

+

dla zwierciadła

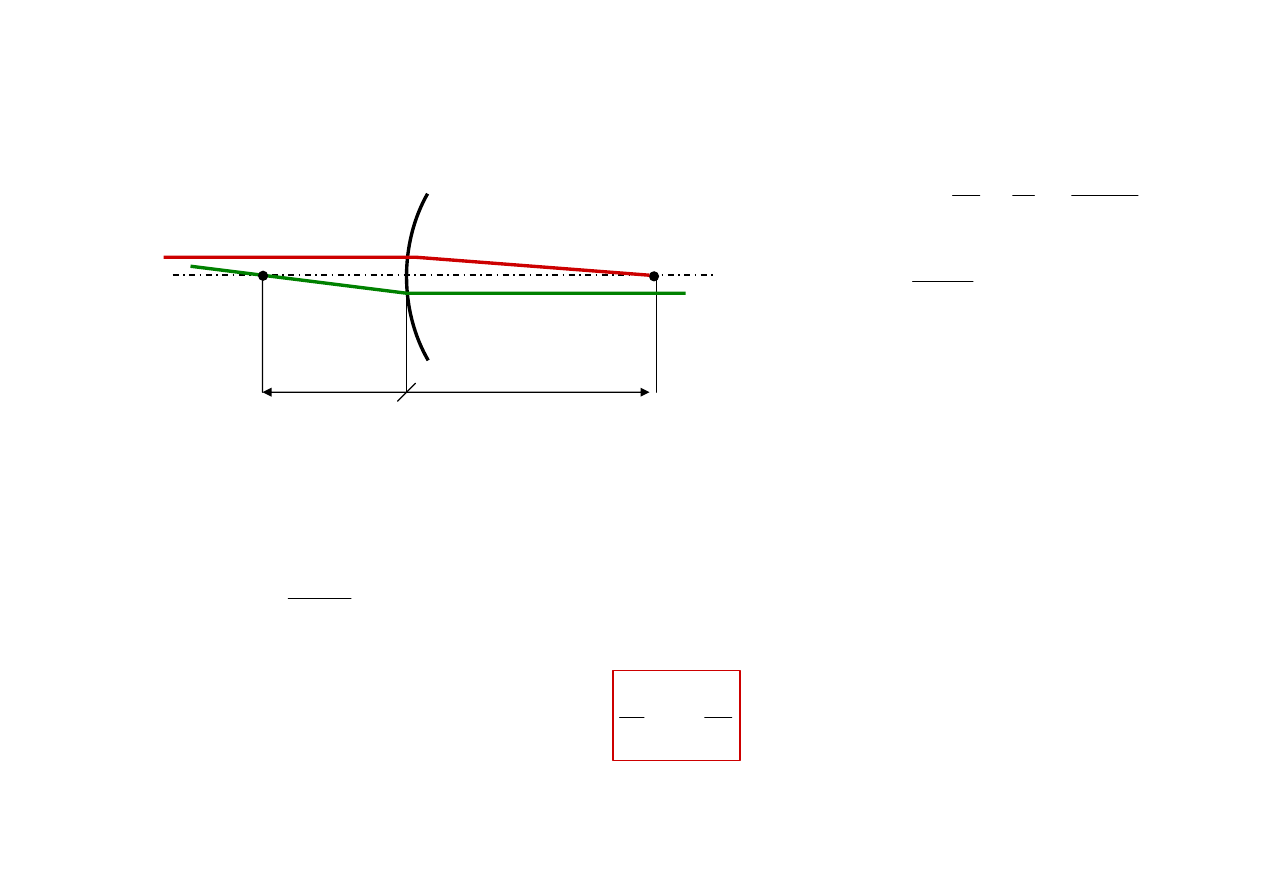
Zwierciadło płaskie

r

→

∞

mamy

s

'

s

−

=

P

P’

-s = - S

s’ = S’

-u

Obraz

P’

bezaberracyjny

S’ = -S

niezależnie od kąta

u

Parametry układu w przestrzeni przyosiowej

Ognisko obrazowe

F’

- obraz punktu leżącego w

∞

(s

→ ∞)

'

f

n

'

n

r

'

n

'

s

'

F

=

−

=

f’

– ogniskowa obrazowa

f

n

'

n

nr

s

F

=

−

−

=

f

– ogniskowa przedmiotowa

Relacja między ogniskowymi

n

'

n

f

'

f

−

=

n

n’ > n

r

n

'

n

s

n

'

s

'

n

−

=

−

Ponieważ

F’

s’

F’

= f’

Ognisko przedmiotowe

F

- punkt, którego obraz leży w

∞

(s’

→ ∞)

-s

F

= -f

F

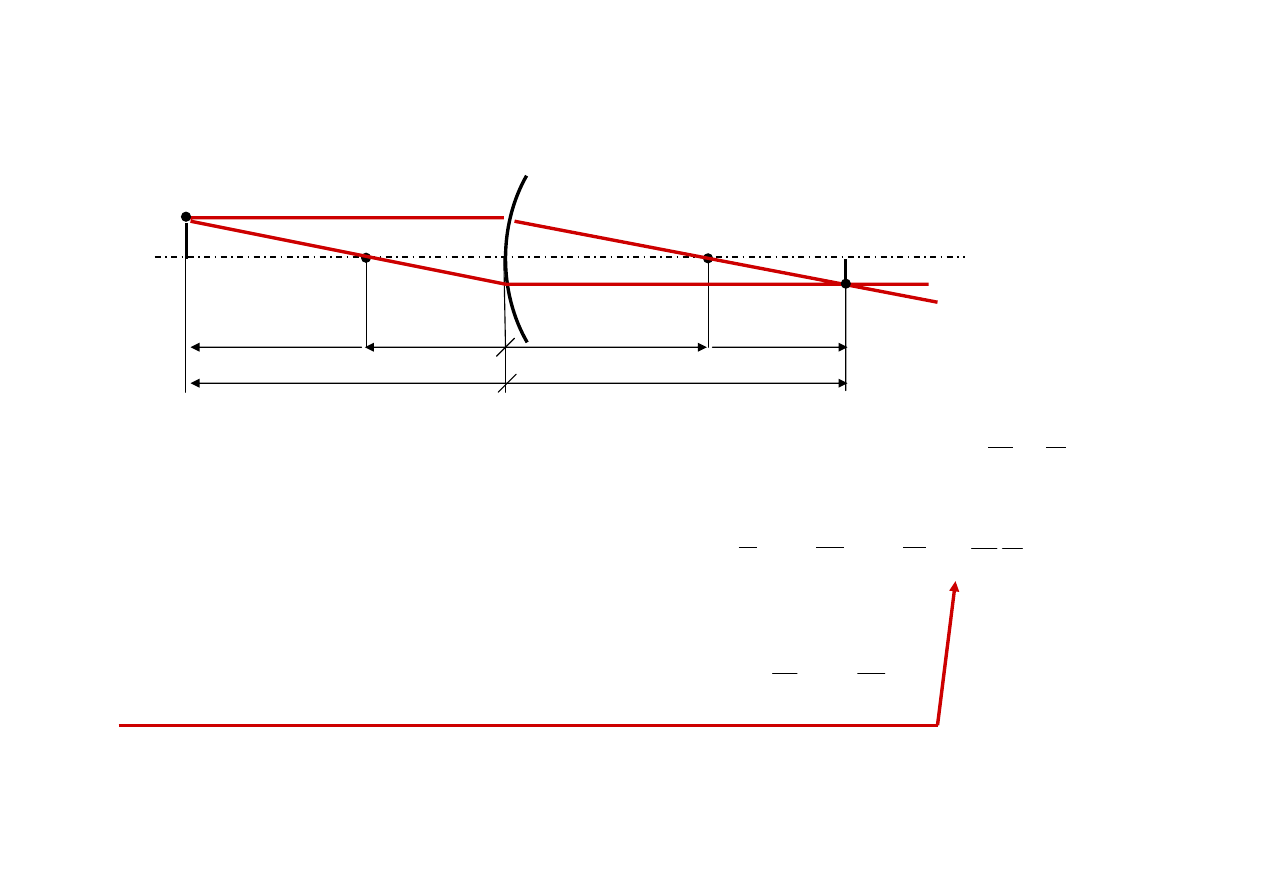
Odwzorowanie przez układ elementarny

w przestrzeni przyosiowej

Powiększenie poprzeczne

x

f

'

f

'

x

l

'

l

−

=

−

=

=

β

Wzór Newtona

'

ff

'

xx

=

Ale

f

s

x

'

f

'

s

'

x

−

=

−

=

→

1

s

f

'

s

'

f

=

+

s

'

s

'

n

n

=

n

n’ > n

F

F’

-f

f’

Przedmiot

P

Obraz

P’

-l’

l

-x

-s

x’

s’

po uwzględnieniu

'

f

'

s

'

x

f

s

x

−

=

−

=

n

'

n

f

'

f

−

=

oraz

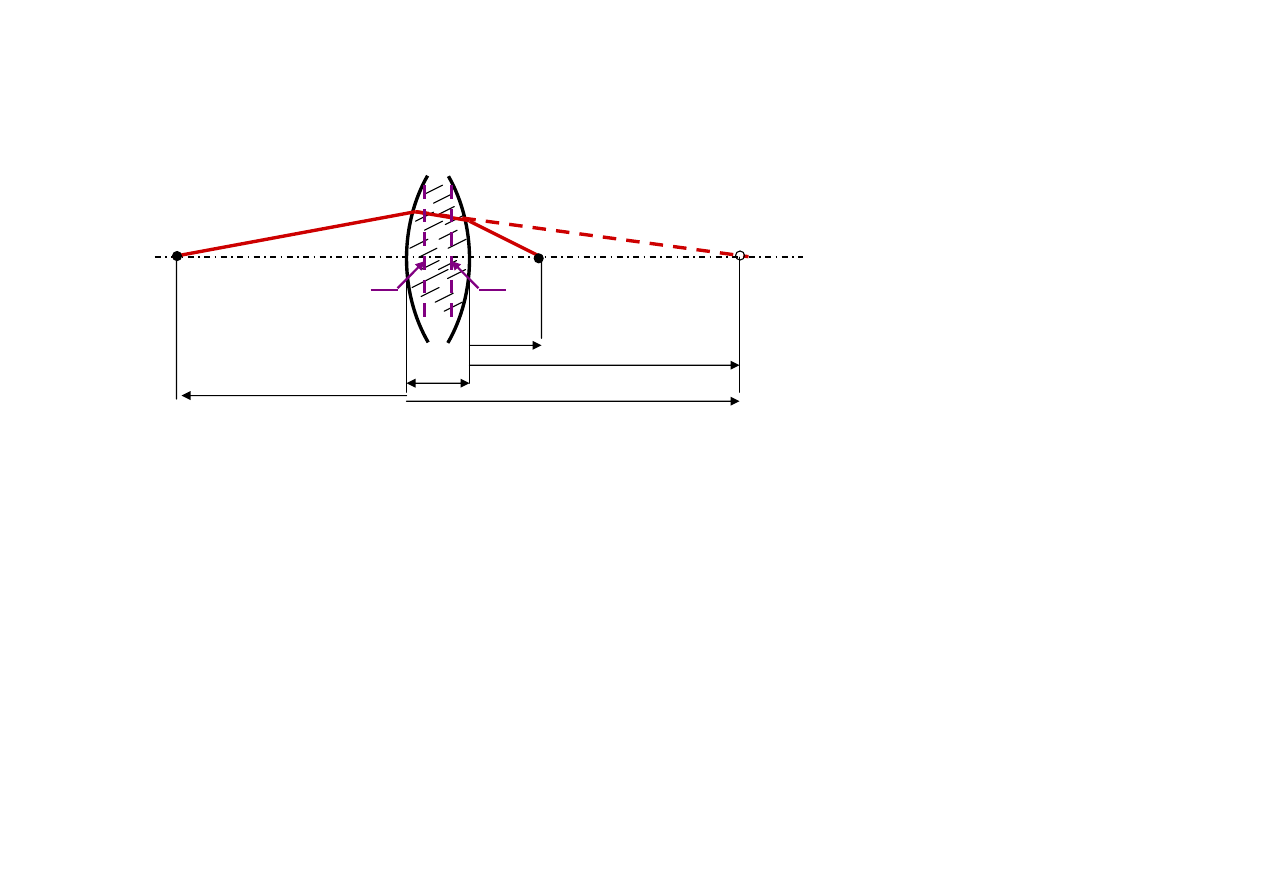
Soczewka w przestrzeni przyosiowej

2

1

β

β

β =

Powiększenie

β

dla soczewki

W celu znalezienia obrazu dawanego przez

soczewkę

wystarczy znać

położenie jej płaszczyzn

głównych

H, H’

i ognisk

F, F’

n = 1

n

n = 1

d

P’

1

≡ P

2

s’

2

P’

2

-s

1

P

1

s

2

s’

1

Płaszczyzny główne

β

H

= 1

H

H’

Dotyczy to również obiektywu, lub innego układu optycznego

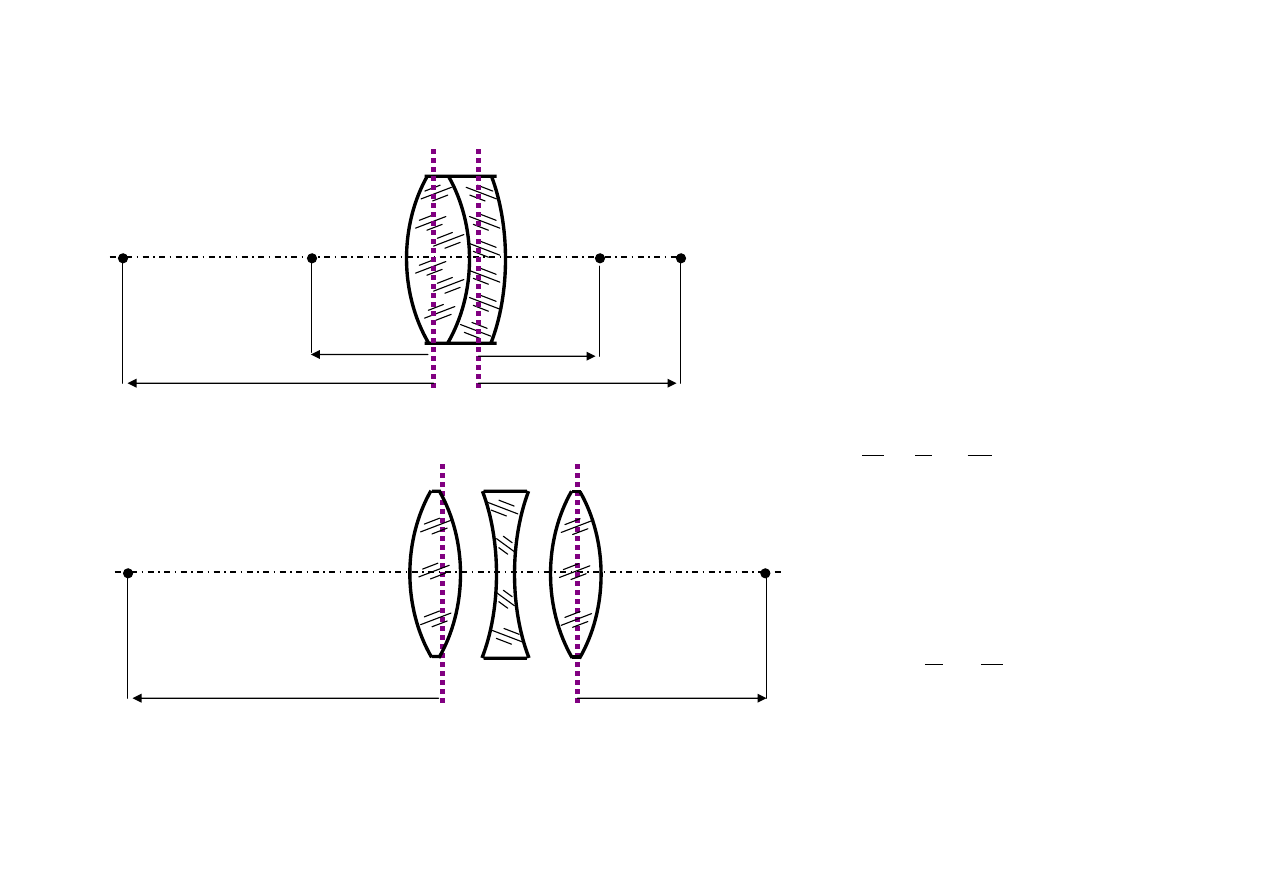
Obiektywy w powietrzu

f’ = -f

Znane ogniskowa

f’

i

położenie

F

i

F’

albo

znane ogniskowa

f’

i

położenie

H

i

H’

f’

f’

s’

-s

F

F’

H

H’

P

P’

s’

-s

H

H’

P

P’

'

f

1

s

1

'

s

1

=

−

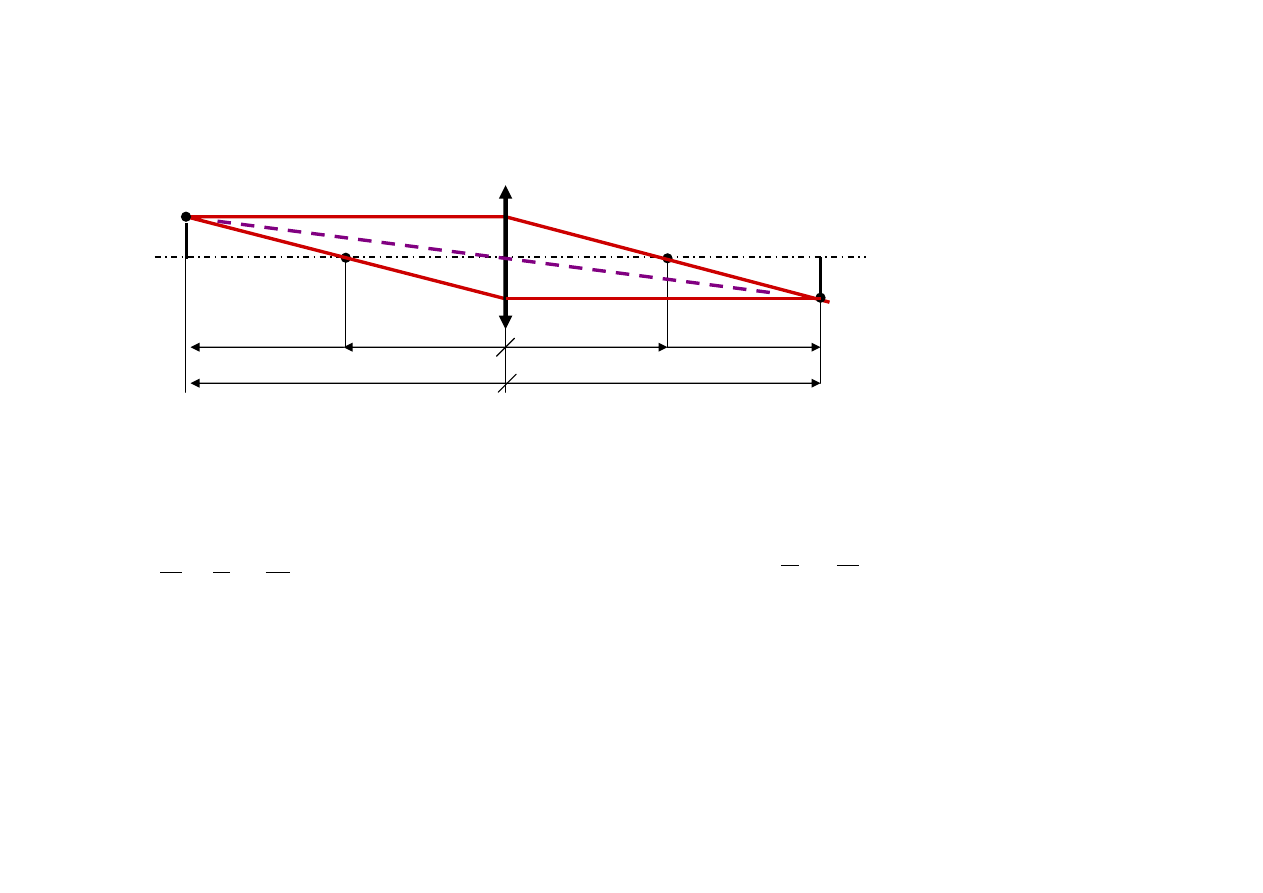
Położenie obrazu

P’

s

'

s

l

'

l =

=

β

Powiększenie

poprzeczne

n = 1

n = 1

F

F’

f’

f’

P

P’

-l’

l

-x

-s

x’

s’

H H’

Obiektyw jako układ cienki

s

'

s

l

'

l =

=

β

Powiększenie poprzeczne

'

f

1

s

1

'

s

1

=

−

Położenie obrazu

P’

2

'

f

'

xx

−

=

lub

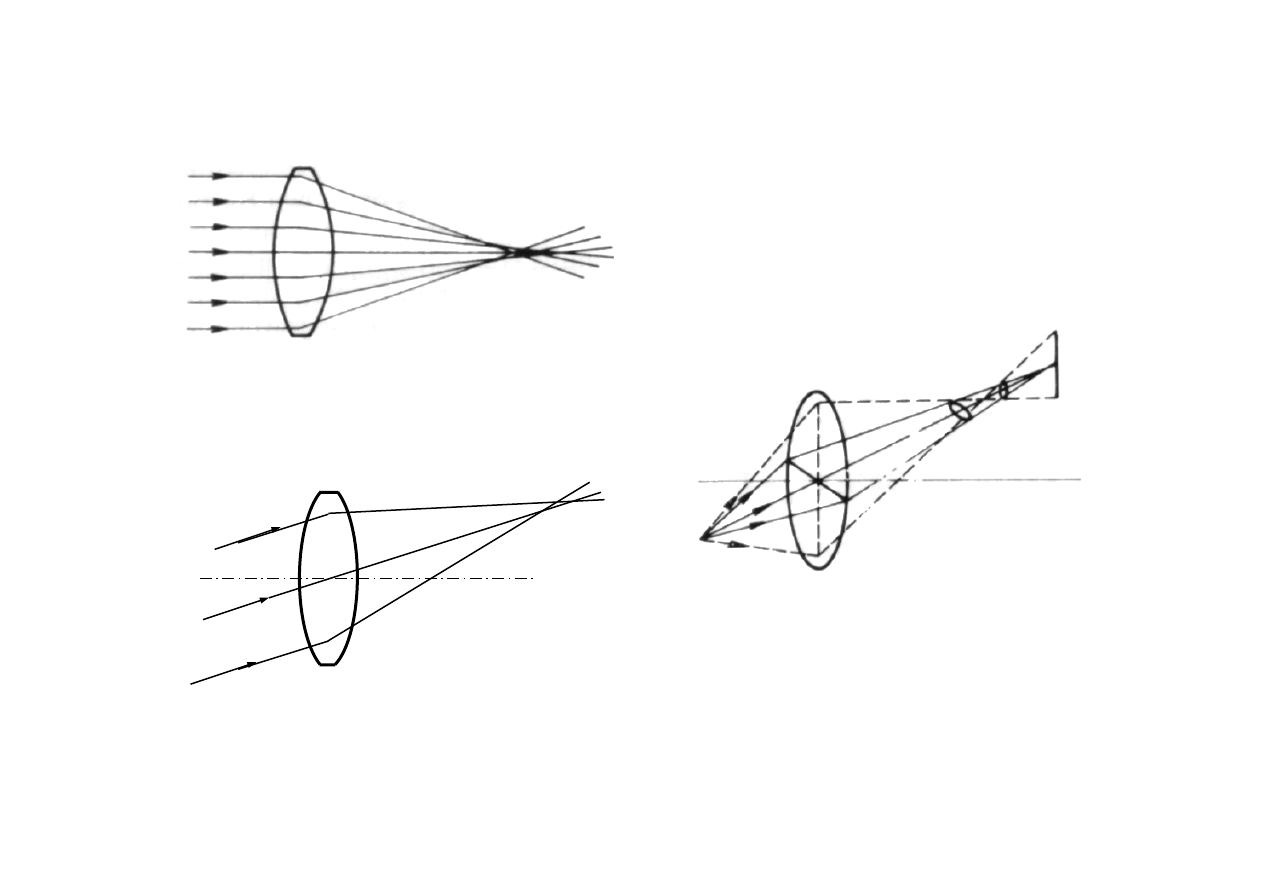
Aberracje obiektywu

- aberracje monochromatyczne

Aberracja sferyczna

Astygmatyzm

Koma

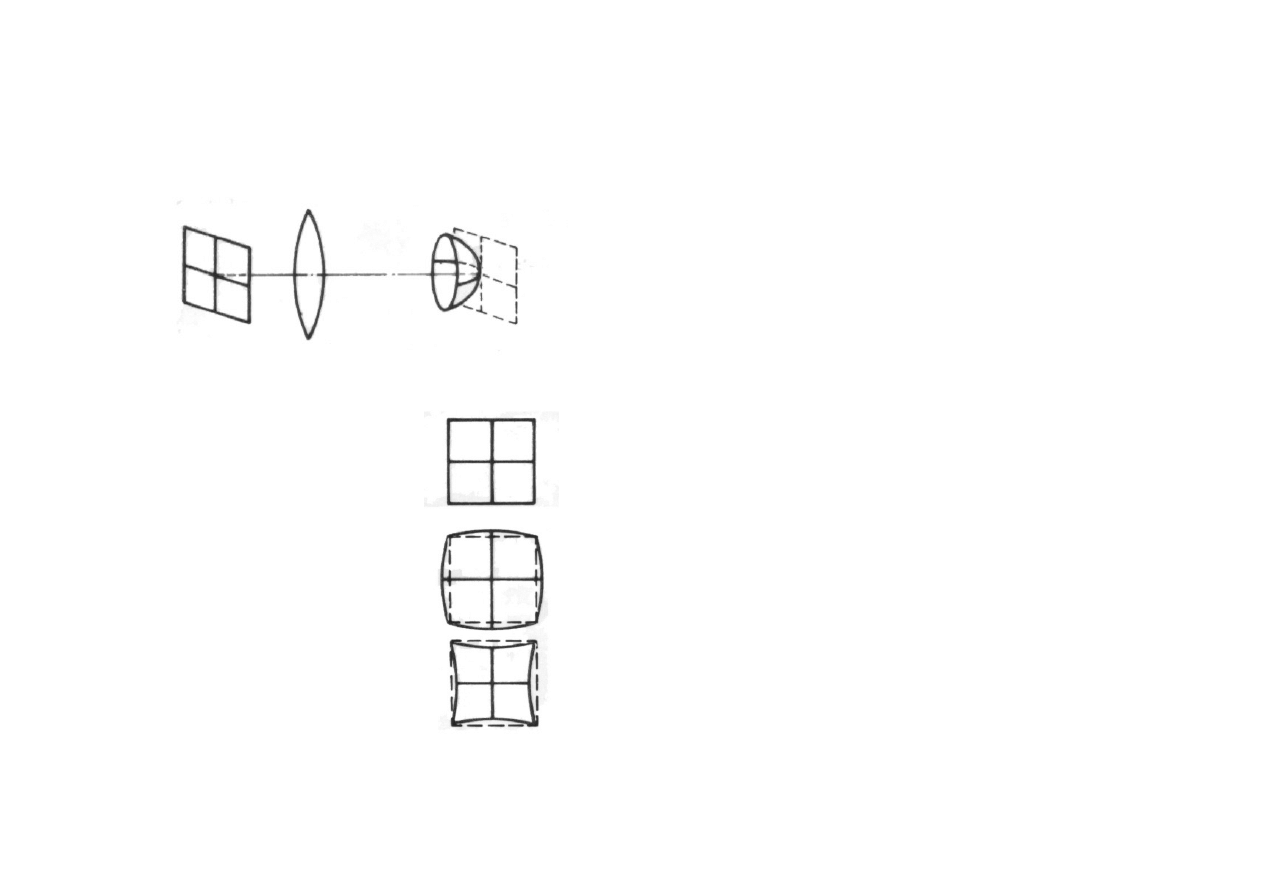
Aberracje obiektywu

- aberracje monochromatyczne cd

Krzywizna pola

Przedmiot

Obraz

Dystorsja

Obraz bezdystorsyjny

beczkowata

jaśkowata

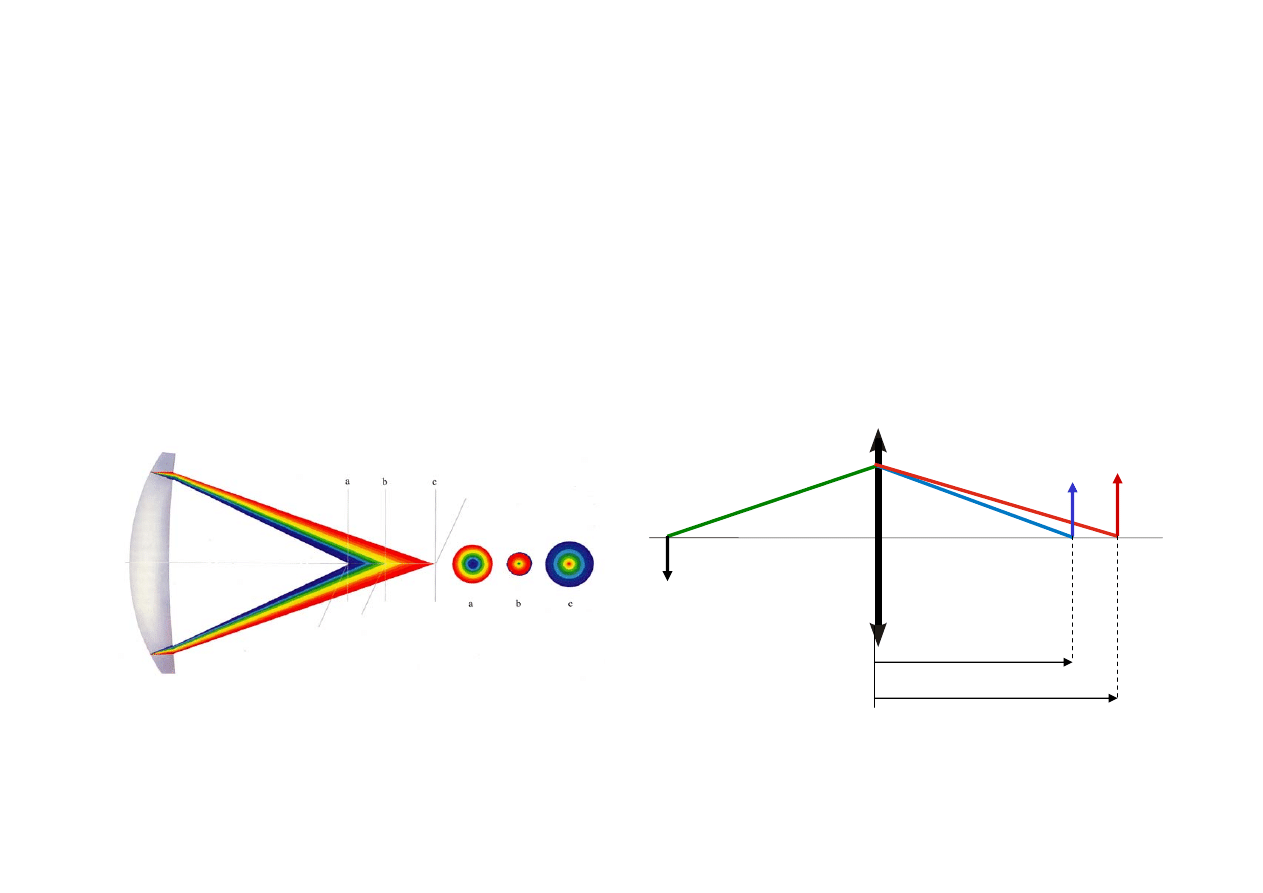
Aberracje obiektywu

- aberracje chromatyczne

Ogniskowa

f’

położenia płaszczyzn głównych

H H’

położenia ognisk

F F’

są funkcjami

λ

↓

położenie obrazu i jego powiększenie są również funkcją

λ

chromatyzm położenia

chromatyzm powiększenia

P

P’

F

P’

C

s’

F

s’

C

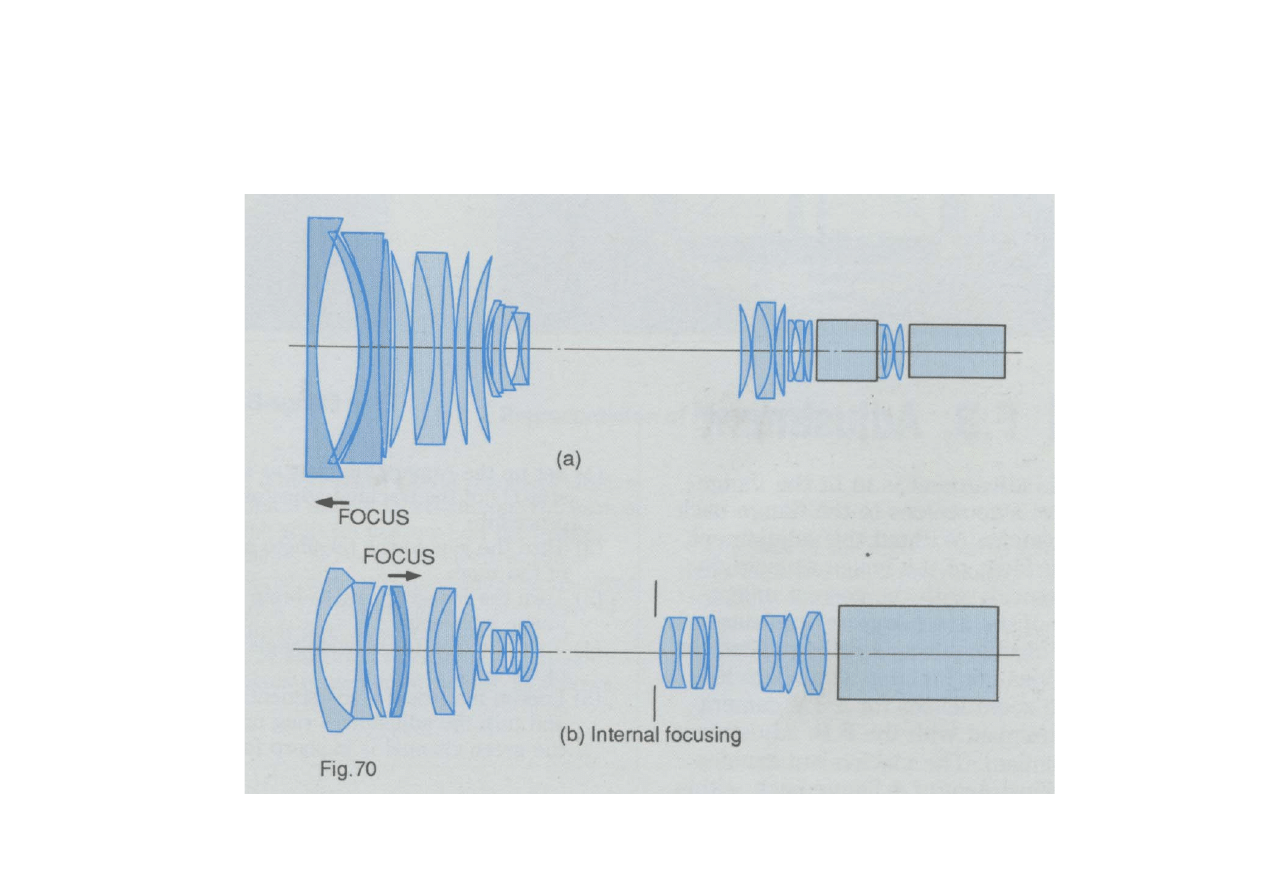
Przykład obiektywu kamery

Aparat fotograficzny

z obiektywem

zmiennoogniskowym

i lampą błyskową

Przyrządy

Powiększenie wizualne

'

f

250

l

250

'

f

l

w

'

w

G

=

=

=

Lupa

Mikroskop

w’

l

w

250

Przedmiot

Nośnik

→

F

l

f’

Ob

Ok

≡ lupa

Nośnik

→

f’

ok

Przedmiot

Obraz dany

przez obiektyw

-w’

ok

ob

ok

ob

G

'f

250

G

β

=

β

=

Powiększenie wizualne

LUPY

Najprostszy mikroskop o małym powiększeniu

Lupy

Powiększenia

G = 2.5 – 10

x

Mikroskop studencki

Mikroskop naukowy

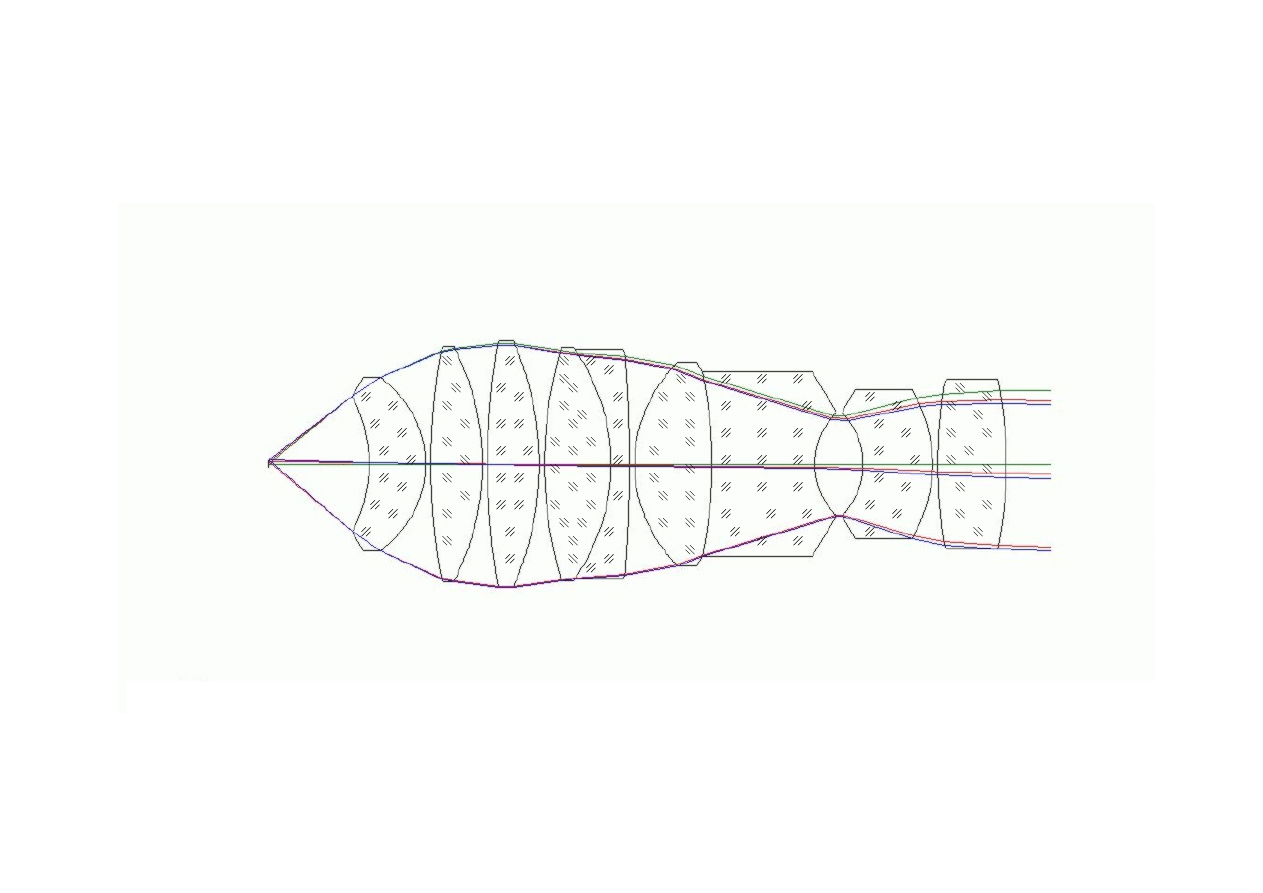
Obiektyw mikroskopowy

Powiększenie

β

ob.

= -40

x

Zaznaczone biegi promieni

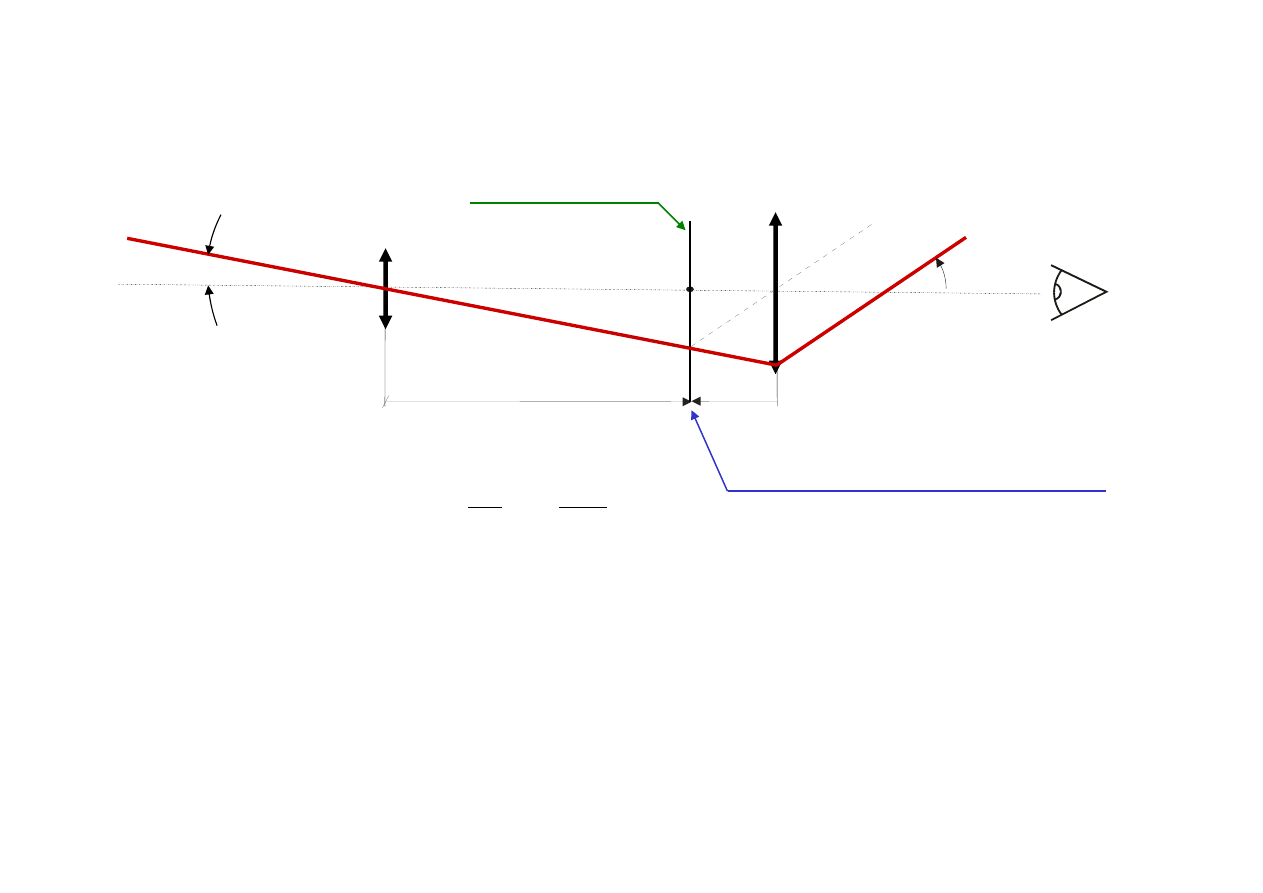
Przyrządy

cd

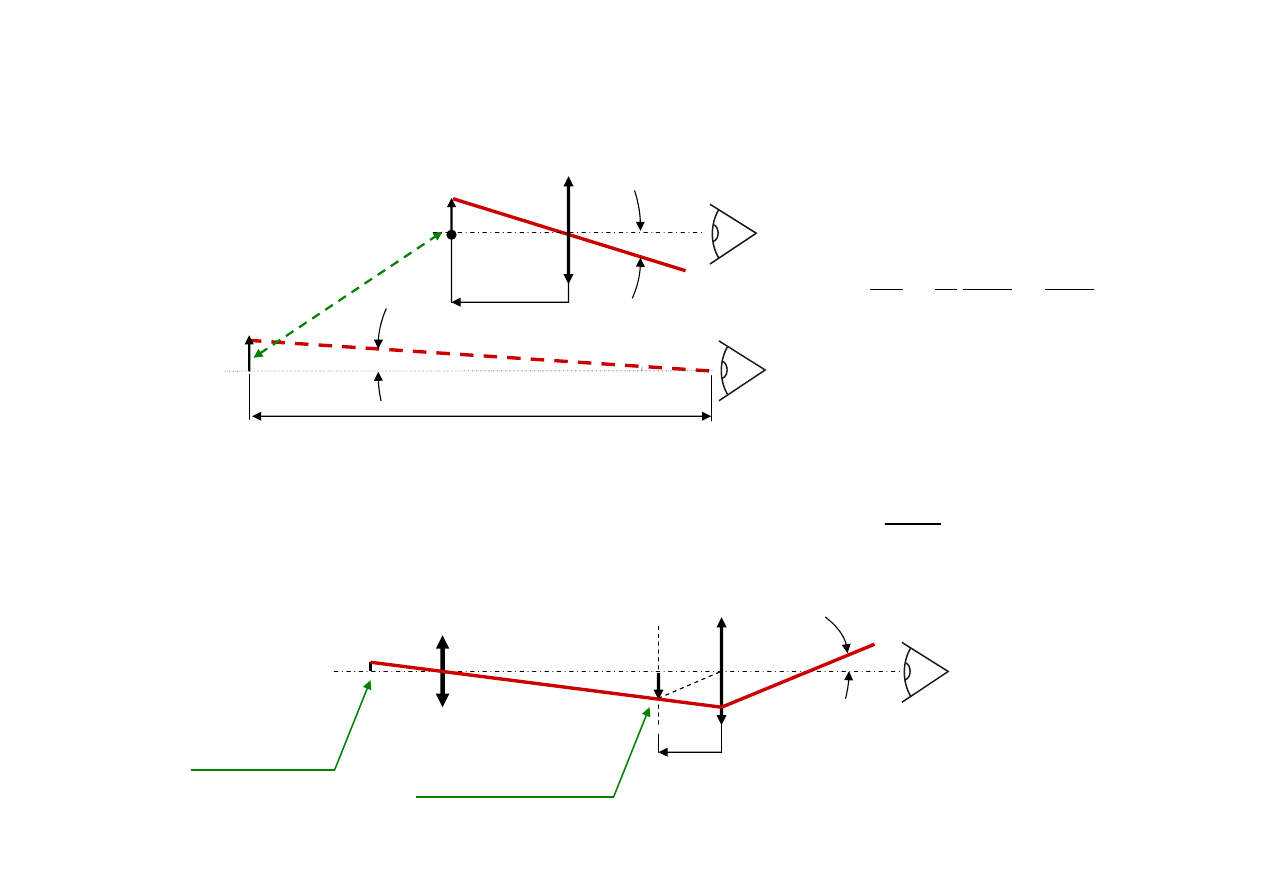
Lunety

←

Przedmiot w

∞

Obraz w

∞

Obraz dany przez

obiektyw

Ob

Ok

F’

ob

f’

ob

F

ok

f’

ok

W płaszczyźnie obrazu płytka z

krzyżem

→

celownik

w

-w’

ok

ob

'

f

'

f

w

'

w

G

−

=

=

Powiększenie

wizualne

Zmierzch przyrządów wizualnych

Profesjonalne układy rejestrują obrazy za pomocą

kamer CCD

–

C

harge Coupled Device

Obraz w komputerze w postaci cyfrowej w celu jego przetwarzania

Lornetka 7x45

Peryskop

Teleskop SALT

w RPA

Współpraca

: Polska, RPA,

Niemcy, Nowa Zelandia,

USA i Wielka Brytania

Średnica zwierciadła

11 m !!!

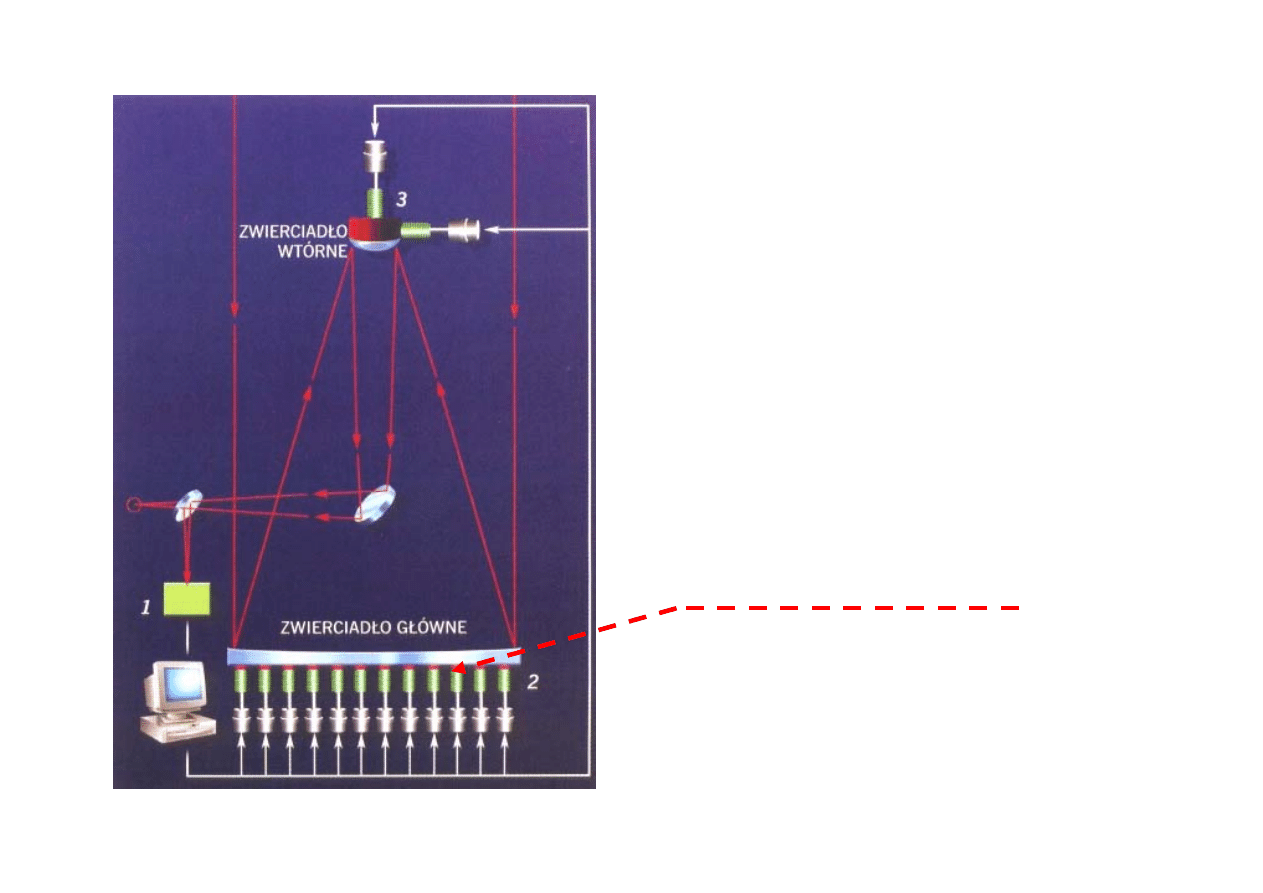
Teleskop SALT

w RPA

Adaptacyjna optyka

91

zwierciadeł o

średnicy

1 m

wysokość

30 m

waga

82 tony

Projektowany jest teleskop o średnicy

100 m

Macierz odbiorników CCD

Typowy wymiar 2.1 x 2.1 mm liczba pikseli 512 x 512

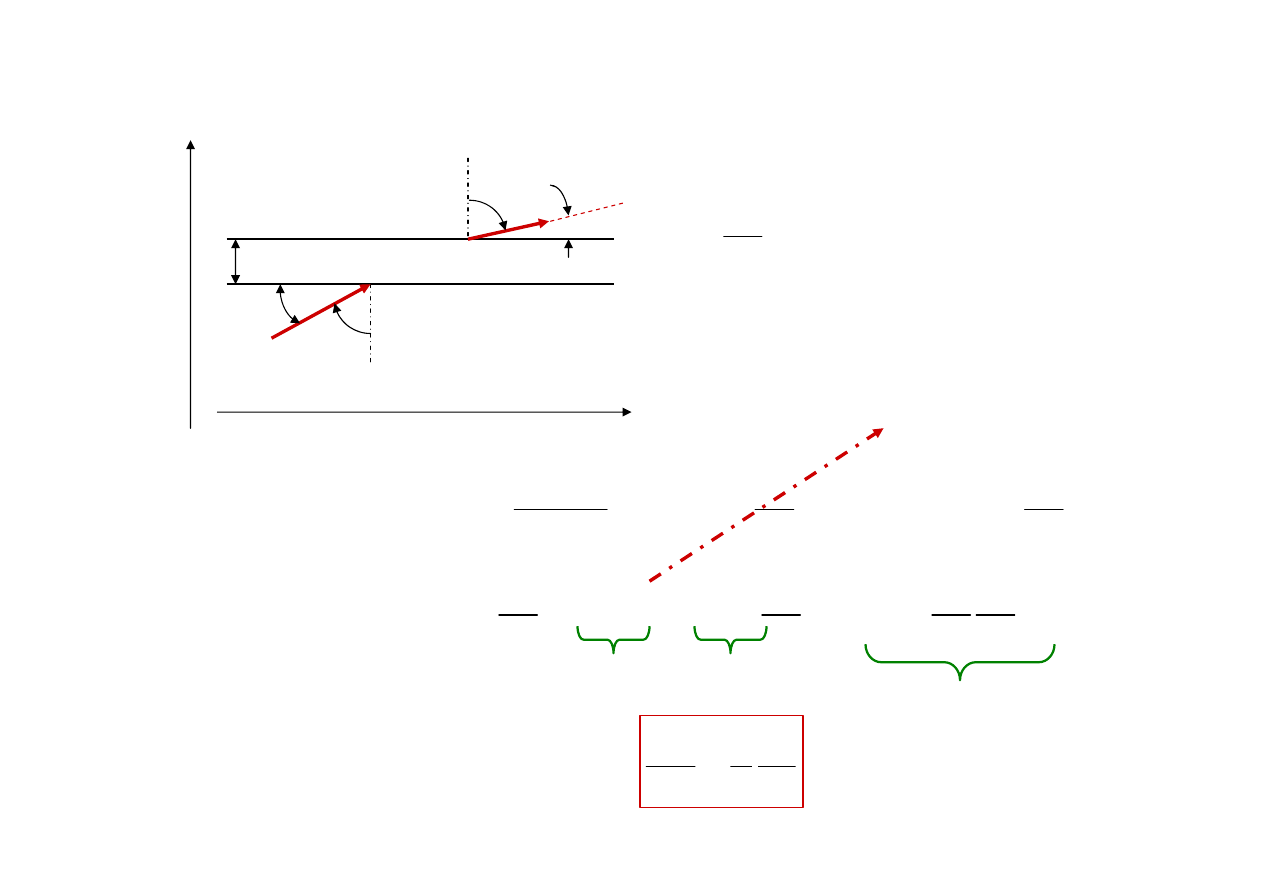
Promień w ośrodku niejednorodnym

Przestrzeń przyosiowa

małe kąty

u

z

Kierunek zmiany

n

r

r

dr

dn

n

'

n

Δ

+

=

Δr

α’

α

u’

n

u

Z prawa załamania

α

=

α

sin

n

'

sin

'

n

ponieważ

α’ = π/2 – u’

oraz

α = π/2 – u

u

cos

n

'

u

cos

'

n

=

⎟

⎠

⎞

⎜

⎝

⎛

Δ

−

⎟

⎠

⎞

⎜

⎝

⎛

Δ

+

=

⎟

⎠

⎞

⎜

⎝

⎛

Δ

+

r

dr

du

u

sin

u

cos

r

dr

dn

n

r

dr

u

cos

d

u

cos

'

n

a więc lewa

strona równania

Po wymnożeniu

2

r

dr

du

dr

dn

u

sin

r

dr

du

u

sin

n

u

cos

r

dr

dn

u

cos

n

Δ

−

Δ

−

Δ

+

pomijalnie mała

wartość

= 1

= u

Ponieważ

u = dr/dz

dr

dn

n

1

dz

r

d

2

2

=

równanie promienia

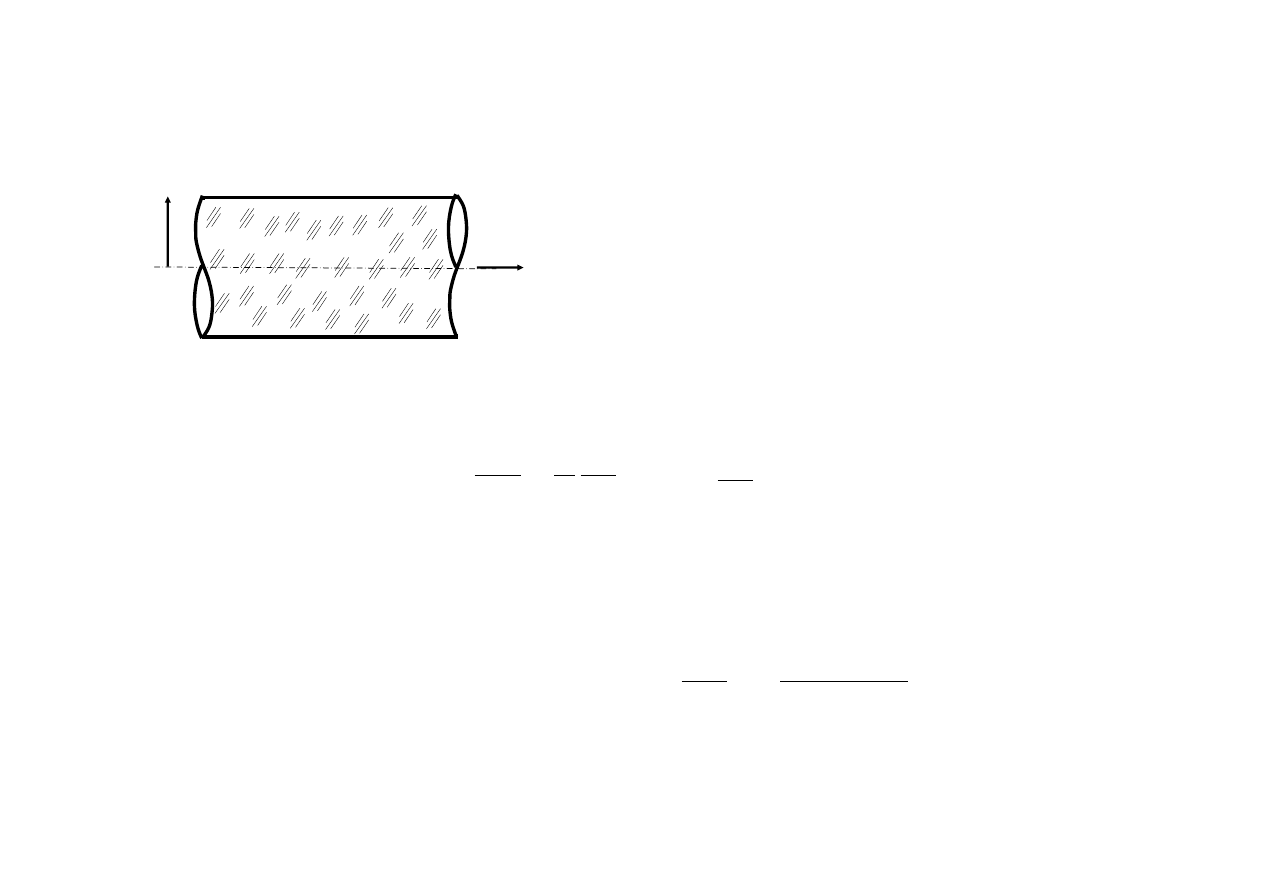
Światłowód gradientowy

r

z

r

a

r

a

5

.

0

1

r

a

dz

r

d

2

2

2

2

2

2

−

≈

−

−

=

i równanie różniczkowe

promienia dla światłowodu

r

a

n

dr

dn

2

0

−

=

więc dla równania

dr

dn

n

1

dz

r

d

2

2

=

→

↓

Niech

(

)

2

2

0

r

a

5

.

0

1

n

n

−

=

1

r

a

5

.

0

2

2

<<

przy czym

a

- stała

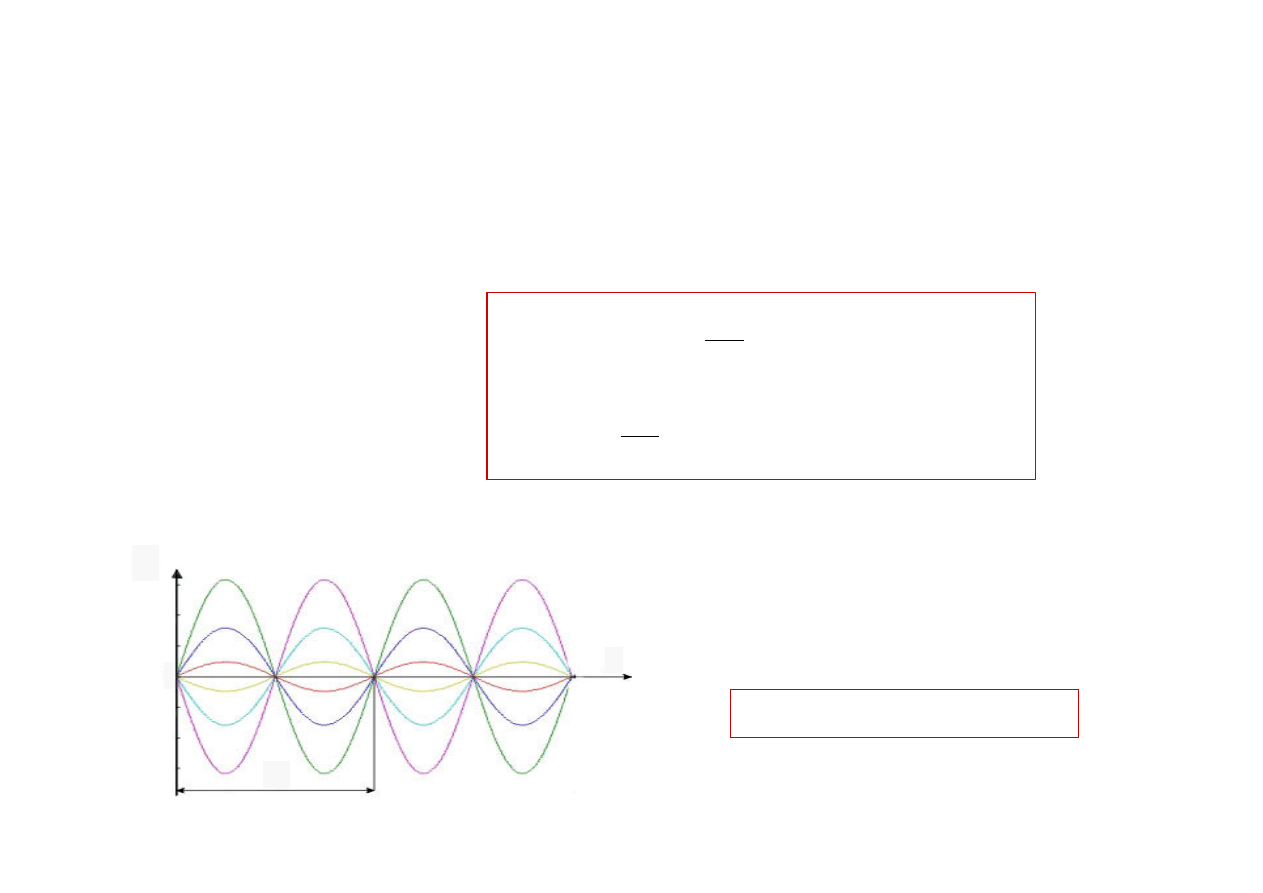
Światłowód gradientowy

Bieg promieni w

światłowodzie dla

z = 0

→

r

0

= 0

dla różnych

u

0

Okres

Y = 2

π/a

( )

( )

( )

( )

az

cos

u

az

sin

a

r

dz

dr

u

az

sin

a

u

az

cos

r

r

0

0

0

0

+

−

=

=

+

=

Rozwiązanie

równania

różniczkowego

niech dla

z = 0

wysokość padania promienia

r = r

0

i kąt

dr/dz = u

0

Warunki początkowe

grad(n)

↓

↑

grad(n)

r

Y

z

0

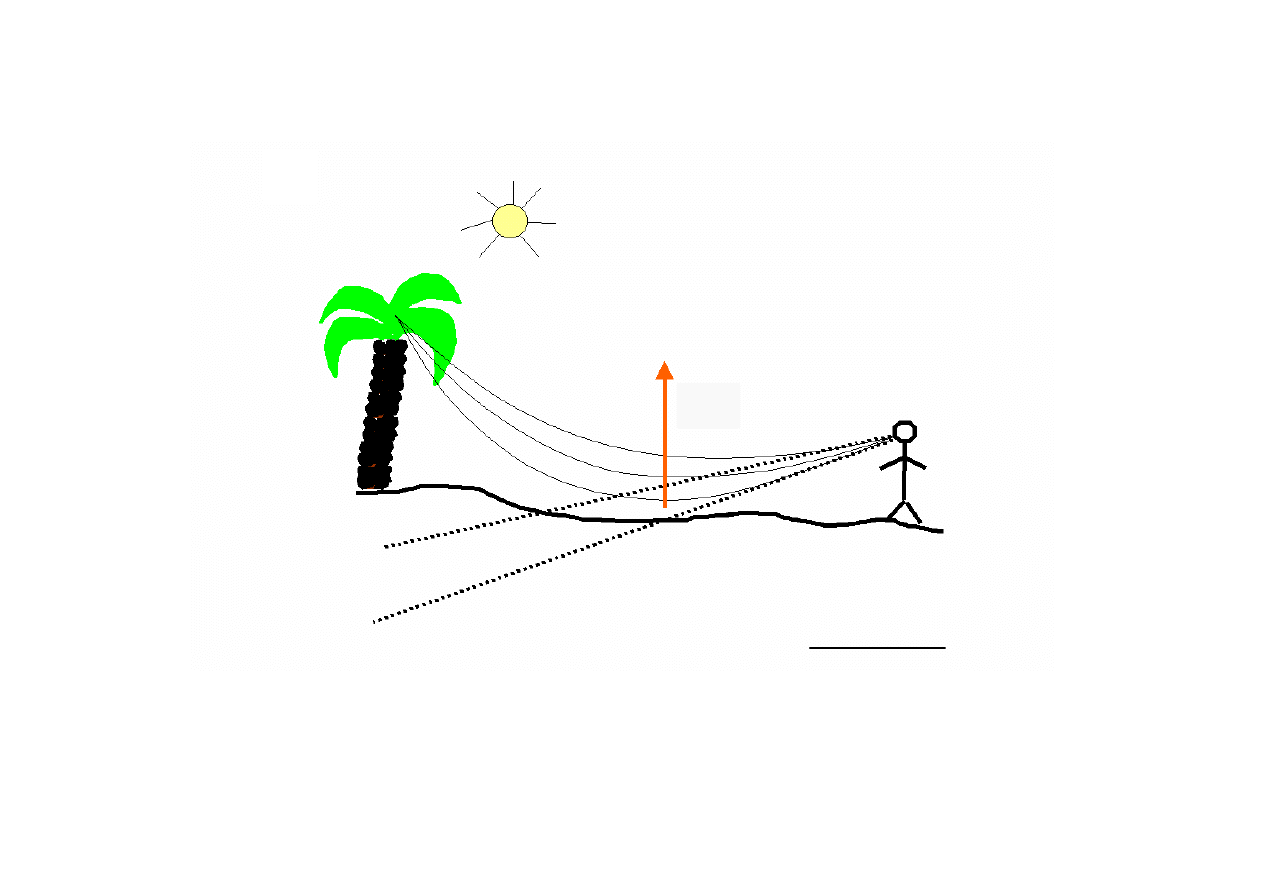
Wpływ gradientów temperatury

grad(n)

273

/

t

1

a

1

n

+

+

≈

t

– temperatura w

0

C

Zjawisko

fata morgana

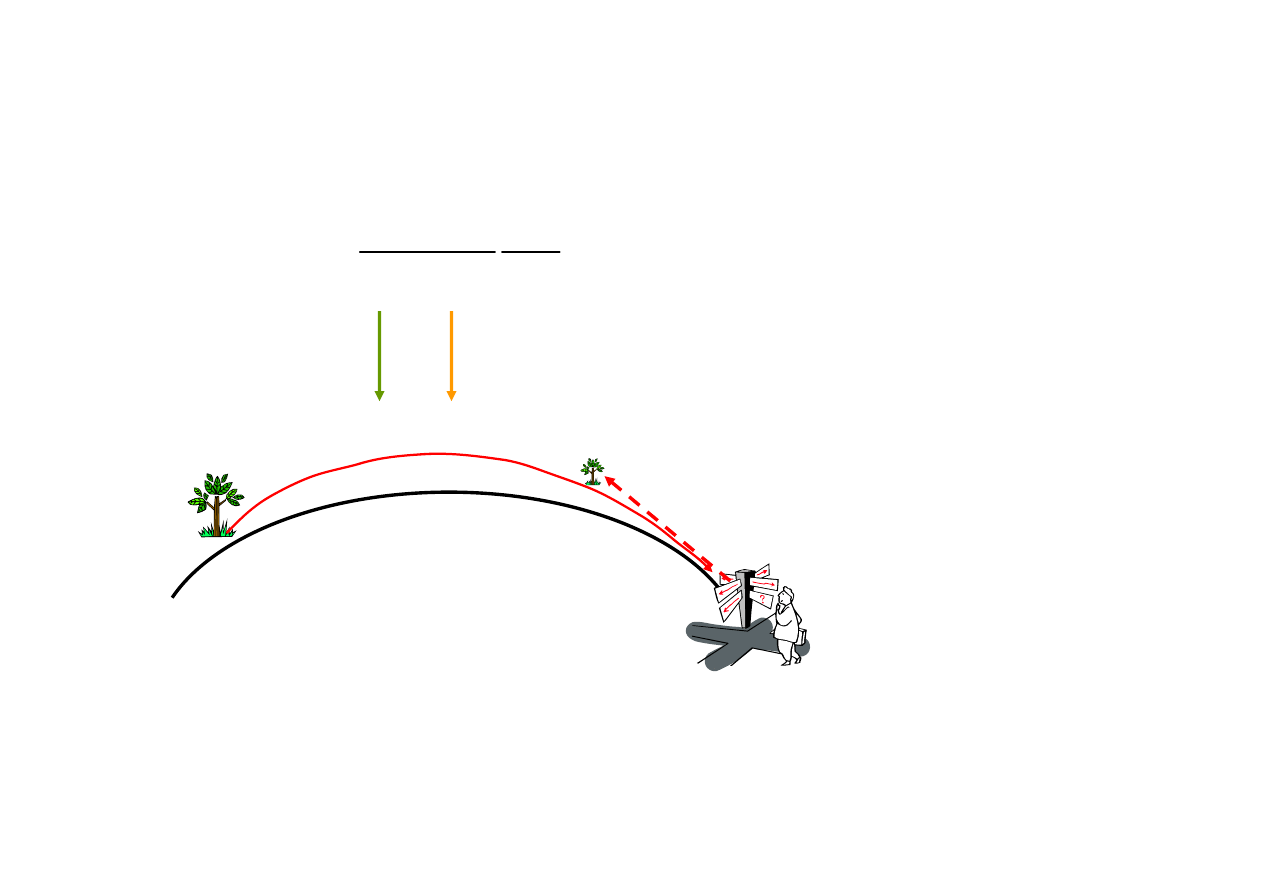
Wpływ gradientów temperatury

Ziemia

t

– temperatura w

0

C

p - ciśnienie

w mm Hg

760

p

273

/

t

1

a

1

n

+

+

≈

grad(p)

grad(n)

Zalety i trudności optyki geometrycznej

Trudności

Brak pojęcia długości fali.

Na podstawie aksjomatów nie można

wyjaśnić rozszczepienia światła przez pryzmat

Promień jest pojęciem geometrycznym

zostawiającym ślad bez

możliwości przypisania mu mocy

Niemożliwe wyznaczenie podziału mocy na wiązkę przechodzącą
i odbitą

Nie wyjaśnia zjawisk

interferencji, dyfrakcji i polaryzacji

Zalety

Prostota pojęć i prostota analizy biegu promieni

zwłaszcza przy wykorzystaniu komputerów

Literatura uzupełniająca

R.Jóźwicki: Optyka instrumentalna. WNT, Warszawa 1970, rozdział

1,

2.

Fragmenty książki, Fundacja Wspierania Rozwoju i Wdrażania Technik
Optycznych

J.R.Meyer-Arendt: Wstęp do optyki. PWN, Warszawa 1977, rozdział 1

E.Hecht, A.Zajac: Optics. Addison-Wesley Publ. Co., Reading Mass. 1974,
rozdział 5

B.E.A.Saleh, M.C.Teich : Fundamentals of Photonics, John Wiley & Sons,
New York 1991, rozdział 1

M.Born, E.Wolf: Principles of Optics. Pergamon Press, Oxford 1980,
rozdział III

Literatura

podstawowa

poziom wyższy

naukowa