Interferencja promieniowania

Zastosowania

Metrologia

Nanotechnologie

Czujniki

szczególnie

światłowodowe

Elementy fotoniczne

Wyjaśnianie:

generacji modów w laserze

propagacji modów w światłowodach

Generacja femtosekundowych impulsów

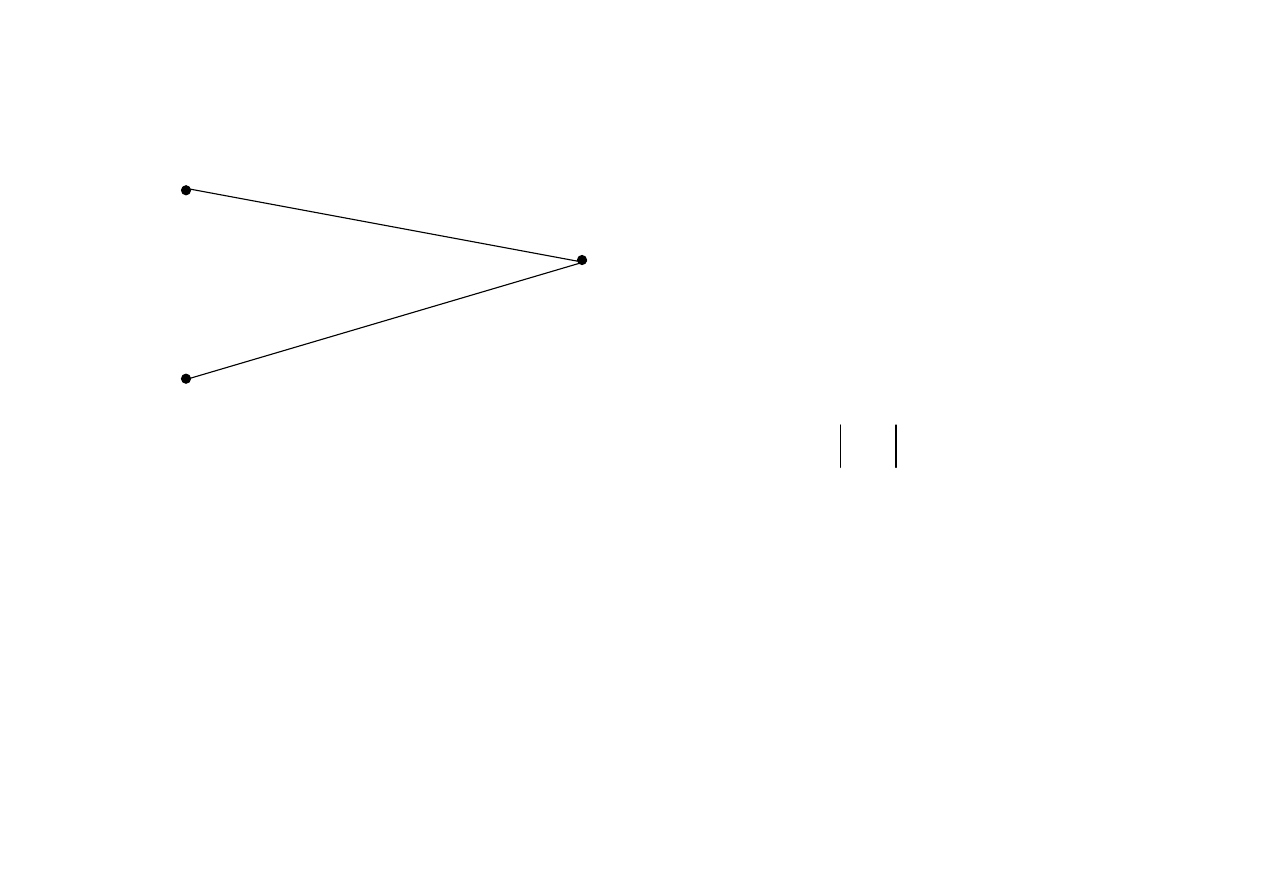
Dwa punktowe źródła

Dwie fale z punktów A

n

,

n = 1, 2

( )

( )

t

i

exp

V

V

t

i

exp

V

V

02

2

01

1

ω

=

ω

=

V

0n

– amplituda zespolona

uwzględniająca początkową fazę

ϕ

n

( )

n

n

0

n

0

i

exp

V

V

ϕ

=

Pole w punkcie

P

po przejściu dróg

r

n

( )

( )

( )

( )

( )

[

]

( )

t

i

exp

ikr

exp

V

ikr

exp

V

ikr

exp

V

ikr

exp

V

t

V

2

02

1

01

2

2

1

1

P

ω

+

=

+

=

Intensywność

→

( ) ( )

t

V

t

V

I

P

P

P

∗

=

Interferencja promieniowania

(

)

[

]

(

)

[

]

2

1

02

01

2

1

02

01

02

02

01

01

P

r

r

ik

exp

V

V

r

r

ik

exp

V

V

V

V

V

V

I

−

−

+

−

+

+

+

=

∗

∗

∗

∗

A

1

A

2

P

r

1

r

2

Interferencja promieniowania cd

(

)

[

]

( )

ϕ

Δ

=

ϕ

−

ϕ

=

∗

i

exp

I

I

i

exp

V

V

V

V

02

01

2

1

02

01

02

01

2

1

ϕ

−

ϕ

=

ϕ

Δ

więc

( )

( )

[

]

ix

exp

ix

exp

I

I

I

I

I

02

01

02

01

P

−

+

+

+

=

gdzie

(

)

ϕ

Δ

+

−

=

2

1

r

r

k

x

02

02

02

01

01

01

I

V

V

I

V

V

=

=

∗

∗

I

0n

jest intensywnością promieniowania w punkcie P

pochodzącego od punktu

A

n

n=1,2

(

)

[

]

(

)

[

]

2

1

02

01

2

1

02

01

02

02

01

01

P

r

r

ik

exp

V

V

r

r

ik

exp

V

V

V

V

V

V

I

−

−

+

−

+

+

+

=

∗

∗

∗

∗

(

)

(

)

ϕ

Δ

−

=

=

∗

∗

∗

i

exp

I

I

V

V

V

V

02

01

02

01

02

01

x

cos

I

I

2

I

I

I

02

01

02

01

P

+

+

=

( )

( )

x

cos

2

ix

exp

ix

exp

=

−

+

gdyż

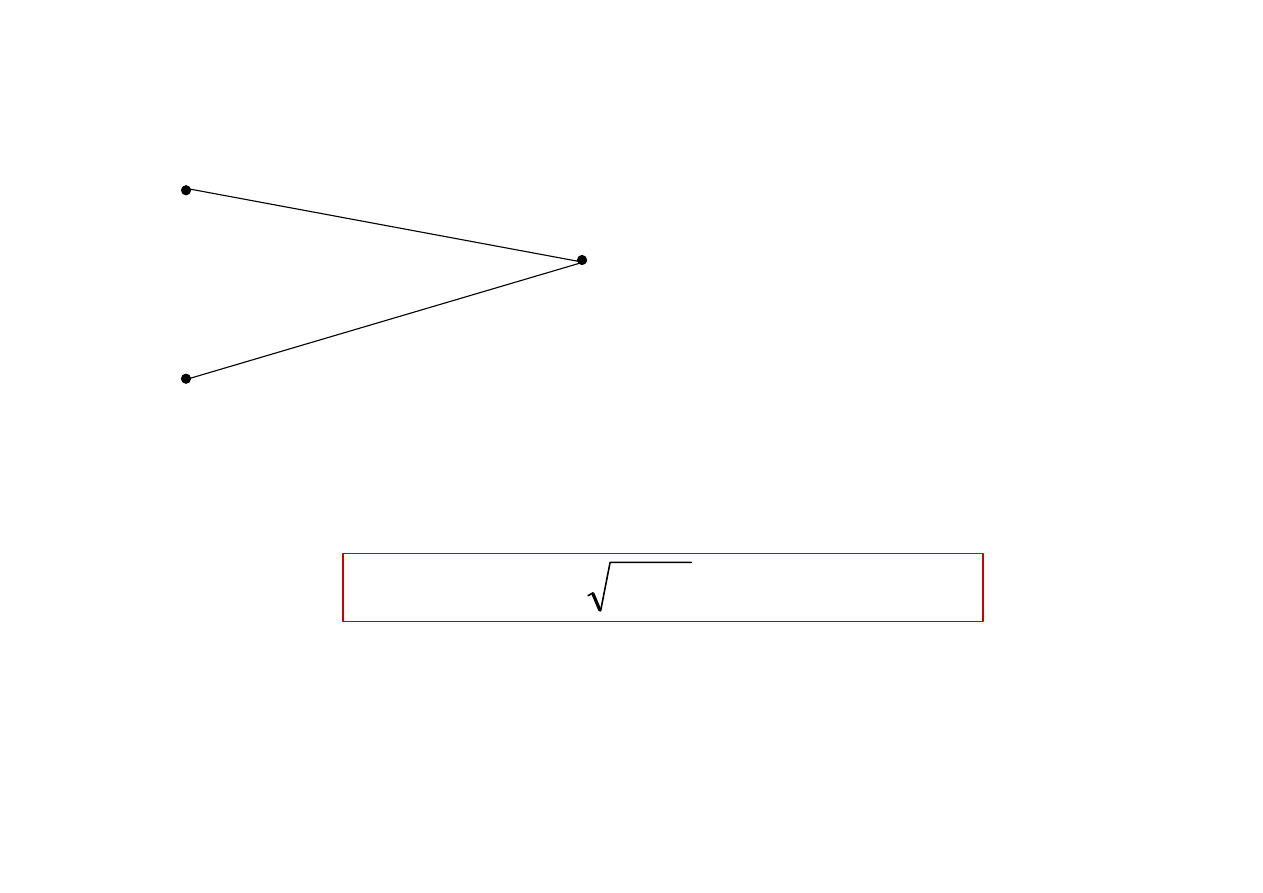
Interferencja promieniowania cd

i ostatecznie wynik interferencji dla 2 punktowych źródeł

(

)

[

]

ϕ

Δ

+

−

+

+

=

2

1

02

01

02

01

P

r

r

k

cos

I

I

2

I

I

I

Δϕ = ϕ

1

-

ϕ

2

różnica faz początkowych obydwu interferujących fal

A

1

A

2

P

r

1

r

2

Fale monochromatyczne emitowane przez 2 atomy

Przypadkowe i niezależne emisje fotonów dla obu źródeł

Fazy początkowe

ϕ

1

(t)

i

ϕ

2

(t)

są przypadkowymi

i szybkozmiennymi funkcjami czasu

t

( )

(

)

( )

[

]

t

r

r

k

cos

I

I

2

I

I

t

I

2

1

02

01

02

01

P

ϕ

Δ

+

−

+

+

=

Różnica faz

Δϕ(t)

jest taką samą funkcją,

a więc

Rejestrujemy średnią wartość w czasie

Δt

znacznie dłuższym od

okresu przypadkowych zmian

( )

2

1

t

P

P

I

I

dt

t

I

t

1

I

+

=

Δ

=

∫

Δ

gdyż uśrednienie cos daje wartość zerową

W optycznym paśmie interferencji promieniowania z dwóch

niezależnych źródeł nie można zarejestrować

Fale są niekoherentne (niespójne)

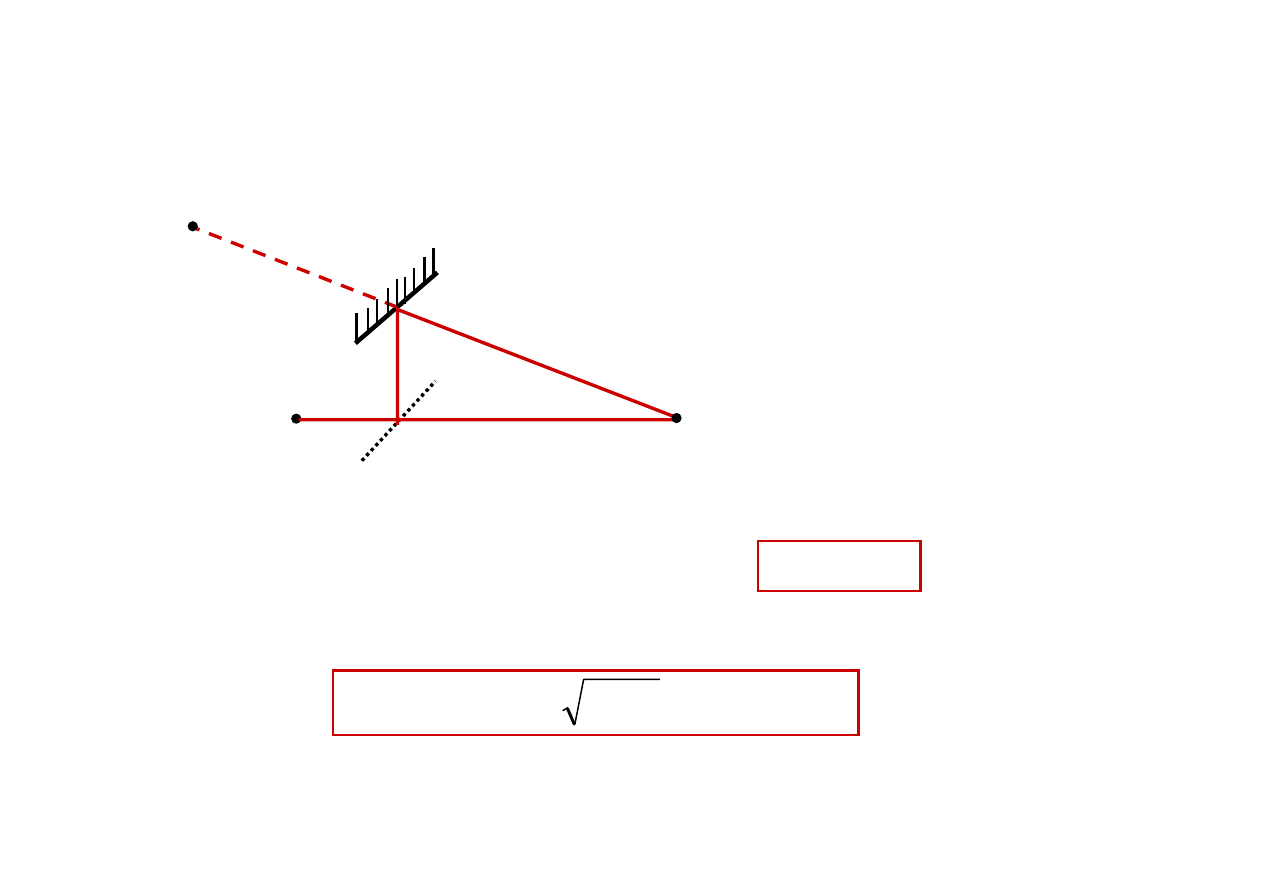
Fala monochromatyczna emitowana

przez punktowe źródło

P

zwierciadło

dzielnik

A

0

≡

A

2

A

1

A

0

–

źródło pierwotne

A

1

i

A

2

– źródła wtórne

2

2

1

1

r

P

A

r

P

A

=

=

Teraz różnica faz początkowych

0

=

ϕ

Δ

(

)

[

]

2

1

02

01

02

01

P

r

r

k

cos

I

I

2

I

I

I

−

+

+

=

Dla różnych położeń punktów

P

stacjonarny rozkład intensywności

Fala monochromatyczna

emitowana przez punktowe źródło cd

Długość fali

λ

w ośrodku o współczynniku załamania

n

vT

=

λ

v

–

prędkość fali

T

–

okres

Oznaczając przez

λ

0

długość fali w próżni, wtedy

0

n

2

2

k

λ

π

=

λ

π

=

n

n

cT

0

λ

=

=

λ

oraz

(

)

m

2

cos

I

I

2

I

I

r

n

2

cos

I

I

2

I

I

I

02

01

02

01

0

02

01

02

01

P

π

+

+

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

λ

Δ

π

+

+

=

Równanie interferencyjne

2

1

r

r

r

−

=

Δ

Oznaczenie

0

r

n

m

λ

Δ

=

rząd interferencji

Iloczyn

nr

jest drogą optyczną, a więc

n

Δr

-

różnicą dróg optycznych

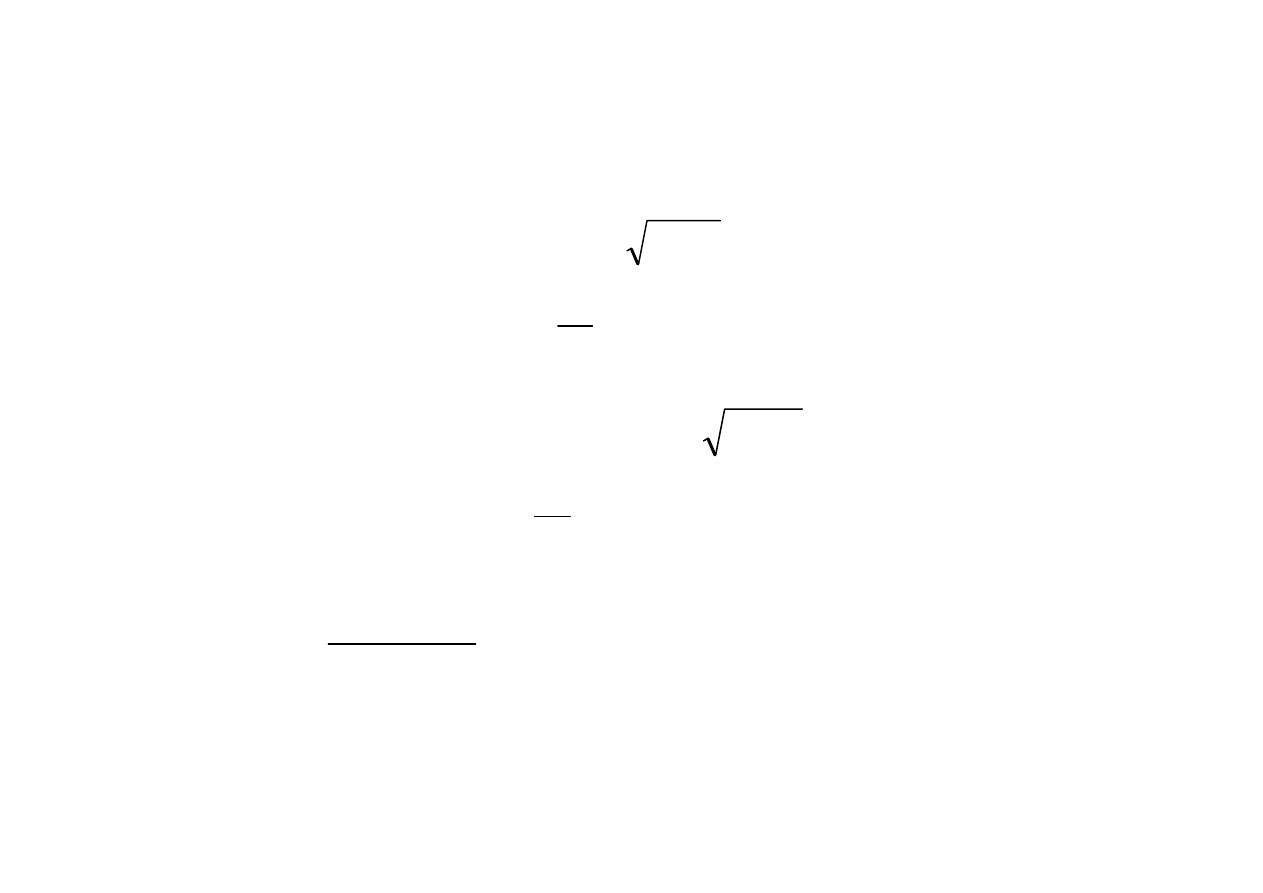
Fala monochromatyczna

emitowana przez punktowe źródło cd

02

01

02

01

max

P

I

I

2

I

I

I

+

+

=

Prążek jasny

gdy cos = 1

→

..

,

2

,

1

,

0

m

lub

K

2

2

r

n

0

±

±

=

λ

=

Δ

Prążek ciemny

02

01

02

01

min

P

I

I

2

I

I

I

−

+

=

(

)

..

5

.

2

,

5

.

1

,

5

.

0

m

lub

1

K

2

2

r

n

0

±

±

±

=

+

λ

=

Δ

gdy cos = -1

→

Kontrast

min

P

max

P

min

P

max

P

I

I

I

I

C

+

−

=

maksymalny

C = 1

gdy

0

02

01

I

I

I

=

=

i wtedy

( )

m

cos

I

4

I

2

0

P

π

=

0

max

P

min

P

I

4

I

0

I

=

=

Interferencja fal emitowanych przez atom

x

A

1

A

2

P

r

1

= r

2

r

1

r

2

π

Atom nie promieniuje światłem

monochromatycznym

W płaszczyźnie

π

dla różnych

długości fal

λ

,

a więc i kołowej

liczby falowej

k

, rozkład

będzie różny,

gdyż

( )

( )

r

k

cos

I

I

2

I

I

k

I

02

01

02

01

P

Δ

+

+

=

Tylko w punkcie

P

dla

Δr = 0

mamy prążek jasny dla

każdego

λ

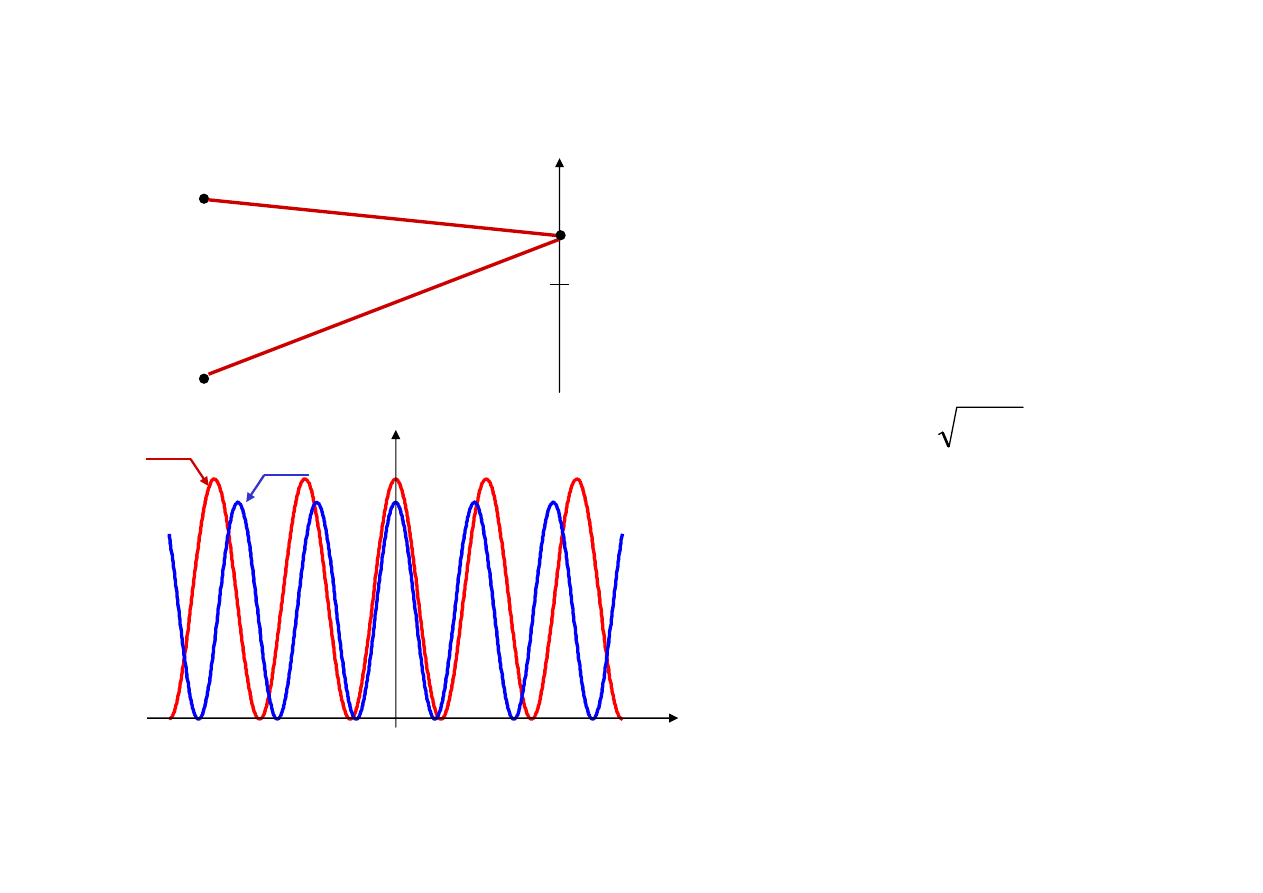
x

Δr = 0

I

P

λ

1

λ

2

λ

2

>

λ

1

Obraz dla 2 długości fal

interferencja.exe

Interferencja w świetle białym

0

x

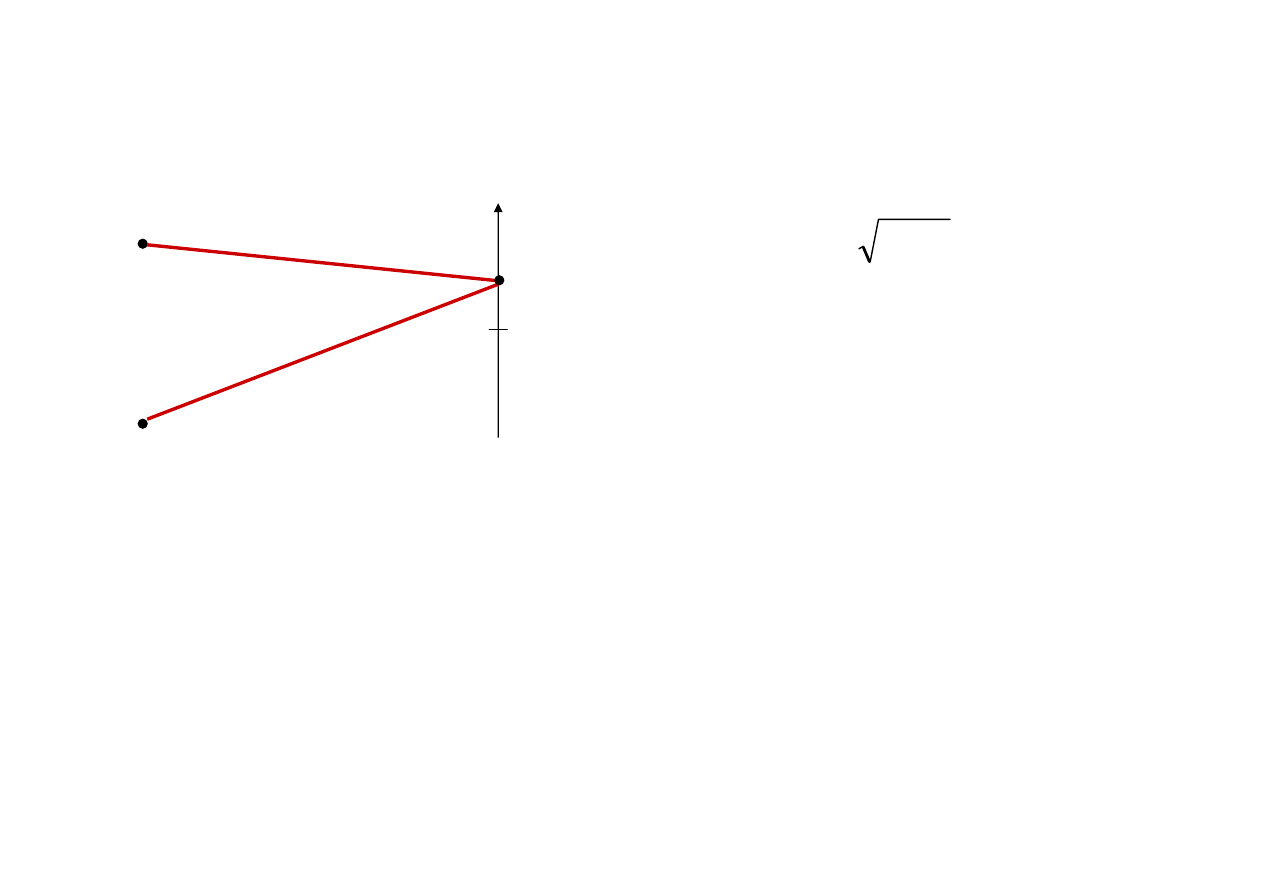
Interferencja fal emitowanych przez źródło punktowe

Wraz ze wzrostem odległości od punktu, dla którego

r

1

= r

2

→

rośnie

Δr

oscylują wartości

cos(k

Δr)

między

+1

a

-1

różnie dla różnych

k

Źródło promieniuje w przedziale

Δλ ∈ (λ

1

,

λ

2

)

i

Δk ∈ (k

1

, k

2

)

( )

( )

r

k

cos

I

I

2

I

I

k

I

02

01

02

01

P

Δ

+

+

=

Odbiornik rejestruje sumę

intensywności dla każdego

k

( )

∫

=

Δk

P

PC

dk

k

I

I

W punkcie

Δr = 0

)

→

max

I

C

P

=

x

A

1

A

2

P

r

1

= r

2

r

1

r

2

π

Kontrast prążków zmniejsza się

Istnieje graniczna odległość

x

g

poza którą kontrast zaniknie

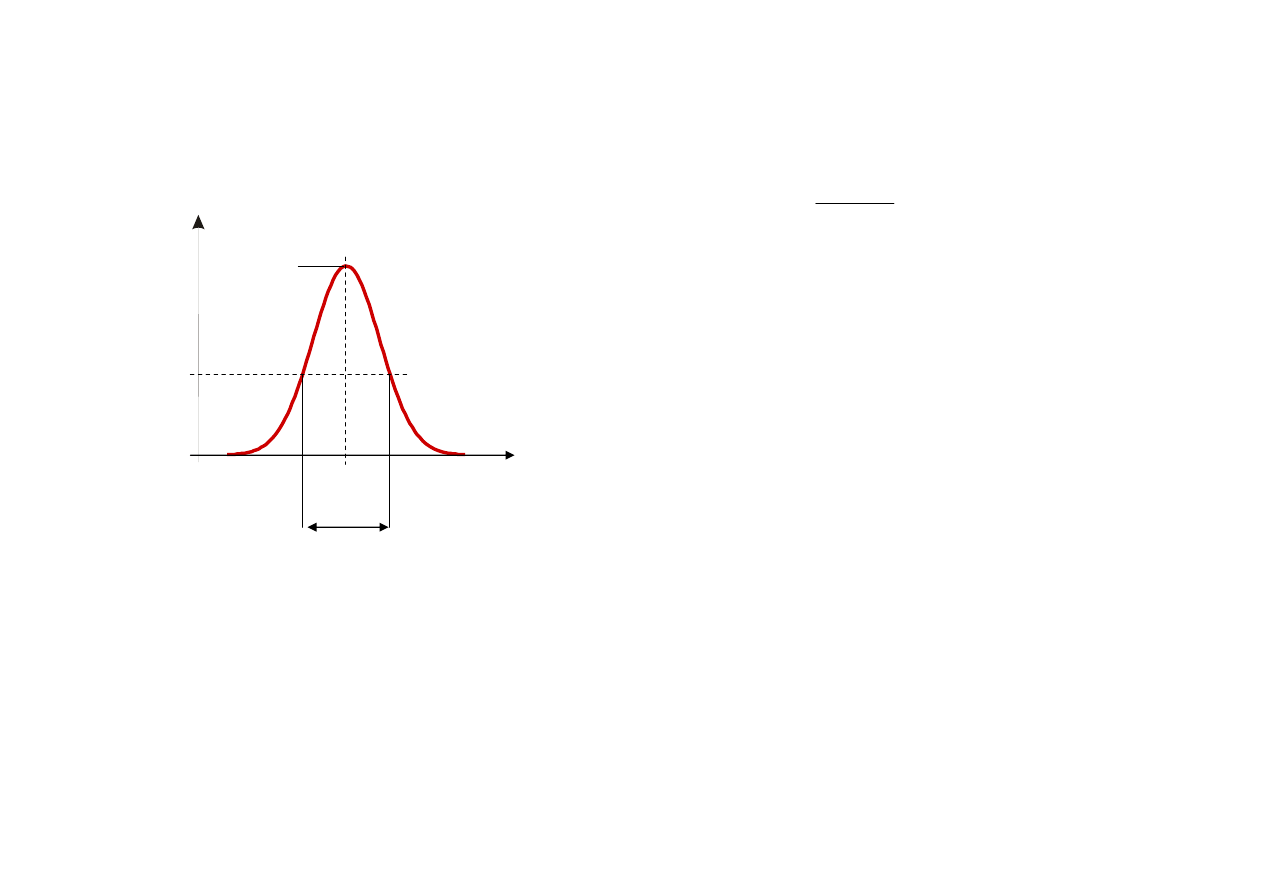
Interferencja fal emitowanych przez atom

przykład

Niech linia spektralna ma postać

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

Δ

−

−

=

2

0

0

k

k

k

k

exp

I

I

k

I

k

k

0

Δk

I

0

Odbiornik rejestruje sumę

intensywności dla każdego

k

( )

∫

=

Δk

P

PC

dk

k

I

I

( )

( )

r

k

cos

I

I

k

I

0

0

P

Δ

+

=

Dla równych intensywności

interferujących fal

I

01

= I

02

= 0.5I

0

otrzymamy dla jednej długości fali

A dla całego widma po rozwiązaniu całki

( )

=

=

∫

Δk

P

PC

dk

k

I

I

(

)

[

]

(

)

{

}

r

k

cos

r

k

5

.

0

exp

1

I

0

2

C

0

Δ

Δ

Δ

−

+

I

0C

– intensywność źródła pierwotnego

(całego widma)

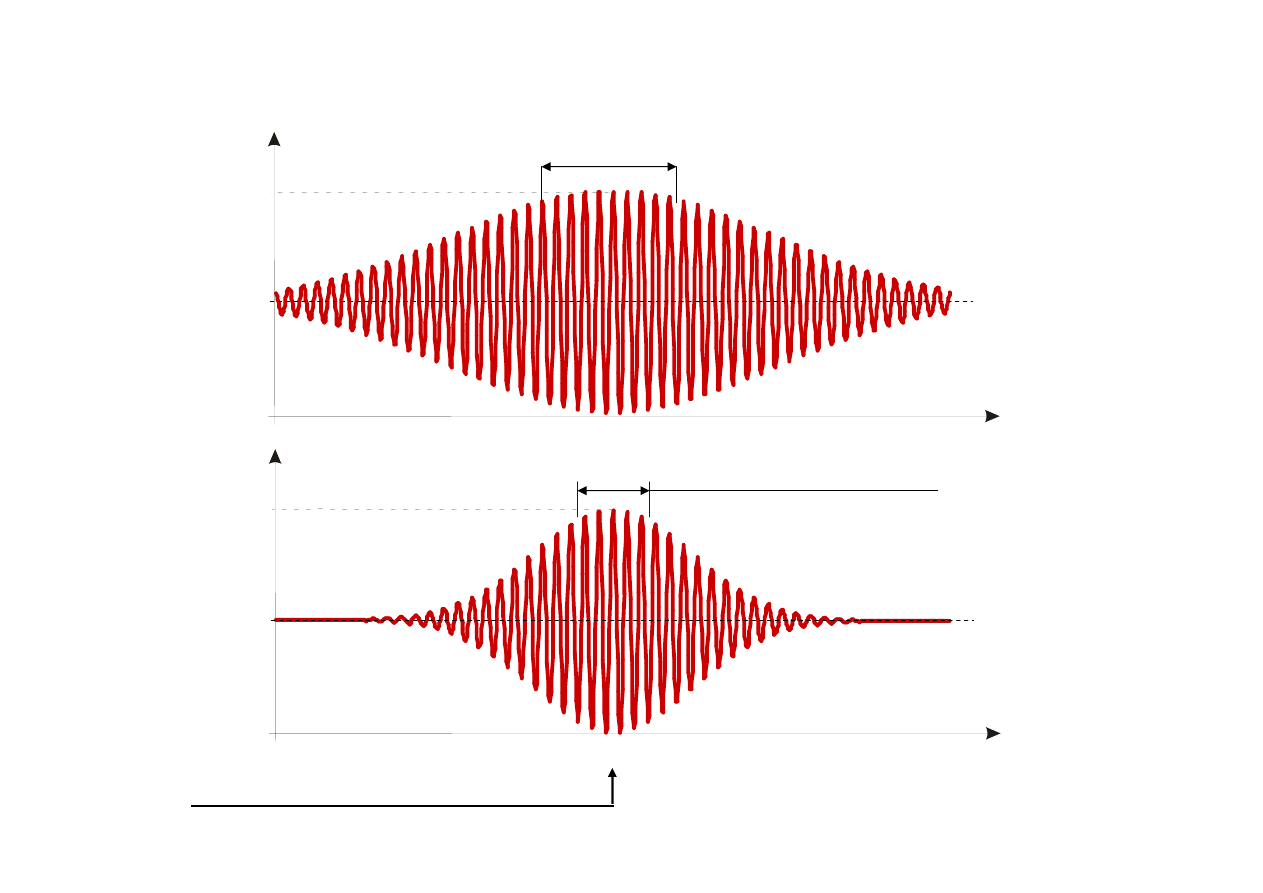
Wynik interferencji dla dwóch wartości

Δk

2

1

I

PC

/I

0C

Δr

0

Δk = 0.02

Δk = 0.04

Δr

0

2

1

0

I

PC

/I

0C

0

2

Δr

g

2

Δr

g

Promieniowanie

niekoherentne

Promieniowanie

quasikoherentne

Promieniowanie koherentne

Interferencja fal emitowanych przez atom

przykład

Wraz ze wzrostem

Δk

maleje

obszar prążków z wysokim kontrastem

Aby uzyskać prążki przy dużej różnicy dróg trzeba stosować

źródła

quasimonochromatyczne

Przełomowa rola laserów

Warunek wysokiego kontrastu

C

≥ 0.9

promieniowanie quasikoherentne

λ

λ

Δ

≈

Δ

=

Δ

10

k

65

.

0

r

2

g

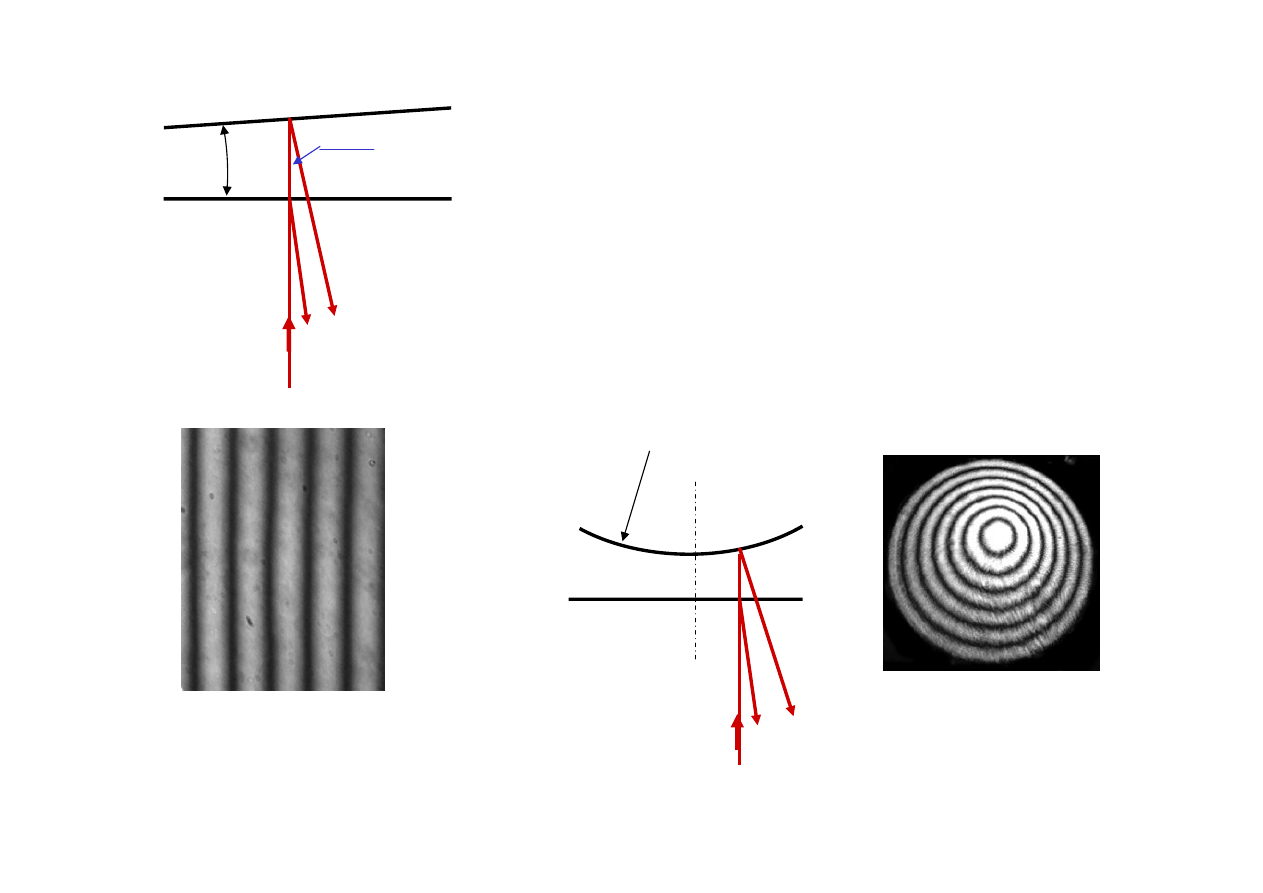
Interferencja promieni odbitych od

dwóch powierzchni

Równanie ciemnego prążka

dla małych

kątów

α

lub dużych promieni

R

(

)

.

.

,

2

,

1

,

0

K

5

.

0

K

h

2

±

±

=

+

λ

=

Obraz prążków

α

2

α

h

Prążki

(Isaac’a)

Newton’a (1642-1727)

R

h

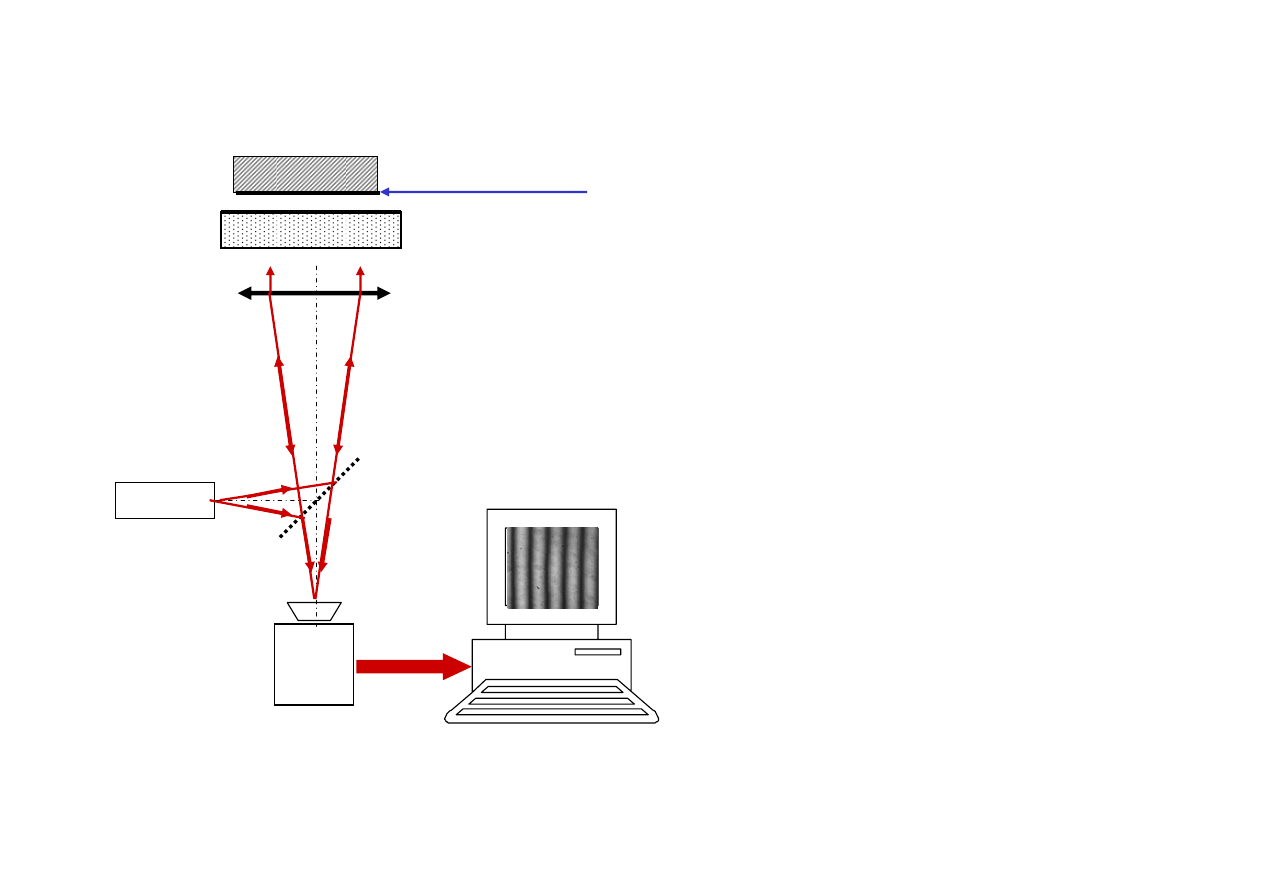
Interferometry

Interferometr

(Hypolite’a)

Fizeau

(czytaj fizo)

(1819-1896)

sprawdzian

powierzchnia

sprawdzana

Ob

laser

dzielnik

CCD

kamera

Program automatycznie

wyznacza kształt powierzchni

sprawdzanej z dokładnością

rzędu

λ/50

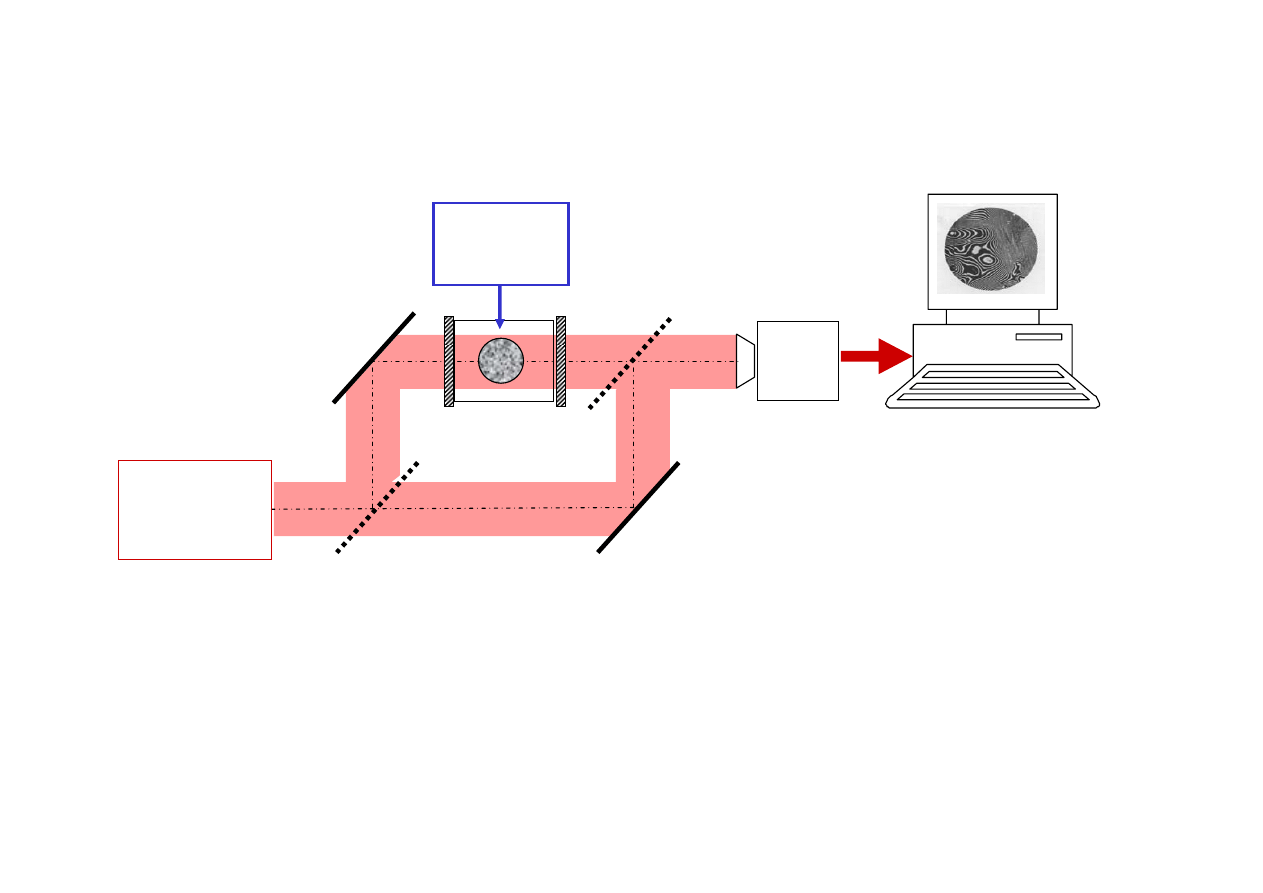
Interferometry

Interferometr (L) Mach’a- (L) Zehnder’a

CCD

kamera

Laser z

układem

optycznym

Kanał

odniesienia

Element

badany

Przykłady

Wpływ konwekcji powietrza

Struga powietrza

Konwekcja powietrza w

płomieniu świecy

Płytka o zmiennej

grubości

Prążki Newtona i płytka

w świetle białym

→

Mucha na

wodzie

Literatura uzupełniająca

Literatura

podstawowa

poziom wyższy

naukowa

M.Born, E.Wolf: Principles of Optics. Pergamon Press, Oxford 1980,
rozdział VII

J.R.Meyer-Arendt: Wstęp do optyki. PWN, Warszawa 1977,
paragrafy 2.2 2.5

E.Hecht, A.Zajac: Optics. Addison-Wesley Publ. Co., Reading Mass.

1974, rozdział 9

B.E.A.Saleh, M.C.Teich : Fundamentals of Photonics, John Wiley &
Sons, New York 1991, paragraf 2.5

R.Jóźwicki: Optyka instrumentalna. WNT, Warszawa 1970, paragraf 3.2.
Fragmenty książki, Fundacja Wspierania Rozwoju i Wdrażania Technik
Optycznych

J.Petykiewicz: Optyka falowa. PWN, Warszawa 1986, rozdział 3