
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
Systemy termiczne to takie, które związane są z przepływem ciepła pomiędzy
substancjami. Przepływ ciepła może odbywać się na trzy sposoby:
przewodzenie ciepła
- polega na przekazywaniu energii przez bezładny ruch
cząsteczek i ich zderzenia
konwekcja – proces przekazywania ciepła związany z makroskopowym
ruchem materii w gazie lub cieczy
promieniowanie - polega na przenoszeniu energii przez promieniowanie
elektromagnetyczne emitowane w wyniku cieplnego ruchu cząsteczek – ma
znaczenie szczególnie tam, gdzie różnica temperatur pomiędzy ciałami jest
bardzo duża
Problematyka przewodzenia ciepła jest ściśle związana z projektowaniem
urządzeń elektronicznych (dobór systemów chłodzenia układów mocy) oraz
energoelektronicznych!
63
Inżynieria systemów dynamicznych
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
Wnikanie ciepła pomiędzy powierzchnią ścianki a gazem lub płynem możemy
opisać równaniem
64
Inżynieria systemów dynamicznych
)
(
G
S
T
T
S
q
-
=
a
gdzie:
q – natężenie przepływu ciepła [W]
α
– współczynnik wnikania ciepła [W/(m
2
K)]
T
S
– temperatura powierzchni ścianki [K]
T
G
– temperatura gazu lub płynu [K]
S – powierzchnia ścianki [m
2
]
UWAGA!
Opisywane zjawisko tylko z pozoru wygląda prosto. Głównym problemem jest
określenie współczynnika wnikania ciepła który zależy od bardzo wielu
czynników. Tymi problemami nie będziemy się zajmowali, w ramach
przedmiotu będziemy chcieli tylko zamodelować mało złożone obiekty.

M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
65
Inżynieria systemów dynamicznych
Pojemność cieplna – ilość ciepła jaką należy doprowadzić do ciała, aby
ogrzać je o jednostkę temperatury
gdzie:
C – pojemność cieplna [J/K]
ΔT – zmiana temperatury [K]
ΔQ – doprowadzona do ciała ilość ciepła [J]
C
P
– ciepło właściwe ciała [J/(kg K)]
V – objętość ciała [m
3
]
ρ – gęstość ciała [kg/m
3
]
r
V
C
T
Q
C
P
=
D
D
=
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
Przykład: Zakładamy, że dysponujemy idealnie zaizolowanym zbiornikiem
cieczy o objętości V [m
3
], w którym zanurzona jest grzałka z mieszadłem
(ciecz jest tak mieszana, że w całej objętości zbiornika ma tę samą
temperaturę T [K]). Do zbiornika dostarczany jest stała ilość cieczy M [kg/s] o
temperaturze T
IN
[K], która po ogrzaniu wydostaje się ze zbiornika (ciecz
wypływająca ze zbiornika ma ze względu na mieszanie temperaturę T [K]).
Zbadać, jak zależy temperatura na wylocie ze zbiornika od temperatury na
jego wlocie (T
IN
[K]) oraz od mocy grzałki (P [W]). Założyć, że gęstość cieczy
(ρ [kg/m
3
]) oraz jej ciepło właściwe (C
p
[J/(kg K)]) są znane i nie zależą od
temperatury.
66
Inżynieria systemów dynamicznych
zimna
ciecz
gorąca
ciecz
T
IN
T
T
P

M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
Pojemność cieplna cieczy w zbiorniku:
Ilość ciepła dostarczana z cieczą dopływającą w czasie dt
Ilość ciepła odbierana przez ciecz na wylocie zbiornika w czasie dt
Ilość ciepła dostarczona przez grzałkę w czasie dt
stąd możemy określić bilans ciepła energii cieczy w zbiorniku
co pozwoli nam na napisanie równania różniczkowego opisującego
analizowany proces
oraz określenie transmitancji:
67
Inżynieria systemów dynamicznych
p
C
V
C
r
=
t
t
T
MC
t
Q
IN
p
IN
d
)
(
)
(
=
t
t
T
MC
t
Q
p
OUT
d
)
(
)
(
=
t
t
P
t
Q
G
d
)
(
)
(
=
{
}
t
t
T
t
T
MC
t
P
t
Q
t
Q
t
Q
CdT
IN
P
OUT
IN
G
d
)
(
)
(
(
)
(
)
(
)
(
)
(
-
+
=
-
+
=
)
(
)
(
1
)
(
d
d
t
T
C
MC
t
P
C
t
T
C
MC
t
T
IN
P
P
+
+
-
=
a
s
b
s
P
s
T
s
G
+
=
=
)
(
)
(
)
(
1
a
s
a
s
T
s
T
s
G
IN
+
=
=
)
(
)
(
)
(
2
C
MC
a
P
=
C
b
1
=
gdzie
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
68
Inżynieria systemów dynamicznych
)
(
)
(
)
(
d
d
t
aT
t
bP
t
aT
t
T
IN
+
+
-
=
Załóżmy, że rozważamy system przepływowego ogrzewacza ciepłej wody o
następujących parametrach :
M=0,1kg/s (=6l/min); V=0,15*10
-3
m
3
(=150ml); Cp=4190J/(kg*K),T
IN
= 288K
(15
o
C), T(0)= 288K (15
0
C), w którym grzałkę o mocy P=15kW załączono w
chwili t=0.
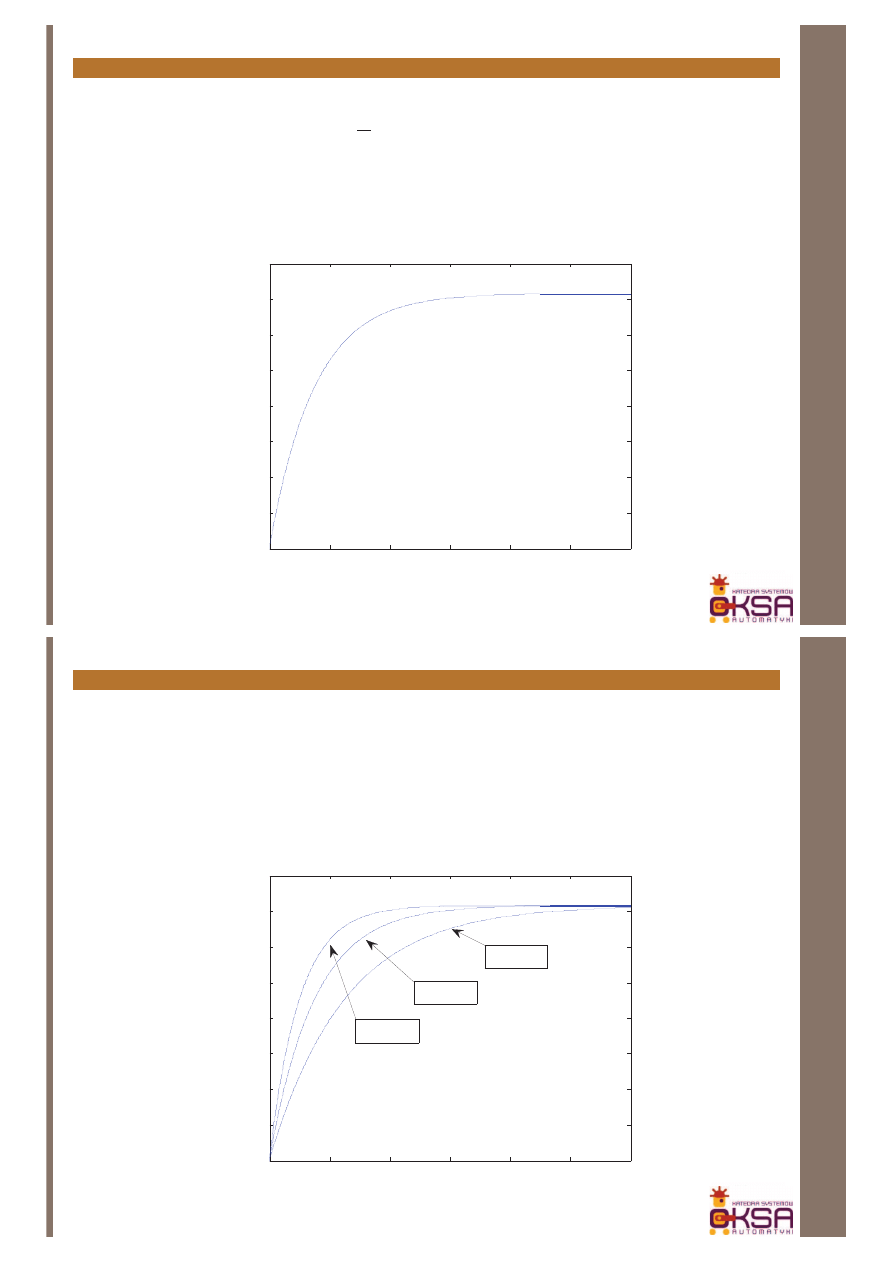
Rozwiązanie powyższego równania dla przedstawionych warunków jest
następujące
)
(
)
1
(
)
1
(
)
0
(
)
(
t
e
P
a
b
e
T
e
T
t
T
at
at
IN
at
1
úû
ù
êë
é
-
+
-
+
=
-
-
-
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
69
Inżynieria systemów dynamicznych
)
(
)
1
(
)
1
(
)
0
(
)
(
t
e
P
a
b
e
T
e
T
t
T
at
at
IN
at
1
úû
ù
êë
é
-
+
-
+
=
-
-
-
0
2
4
6
8
10
12
15
20
25
30
35
40
45
50
55
t [s]
T
(t
)
[°
C
]
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
70
Inżynieria systemów dynamicznych
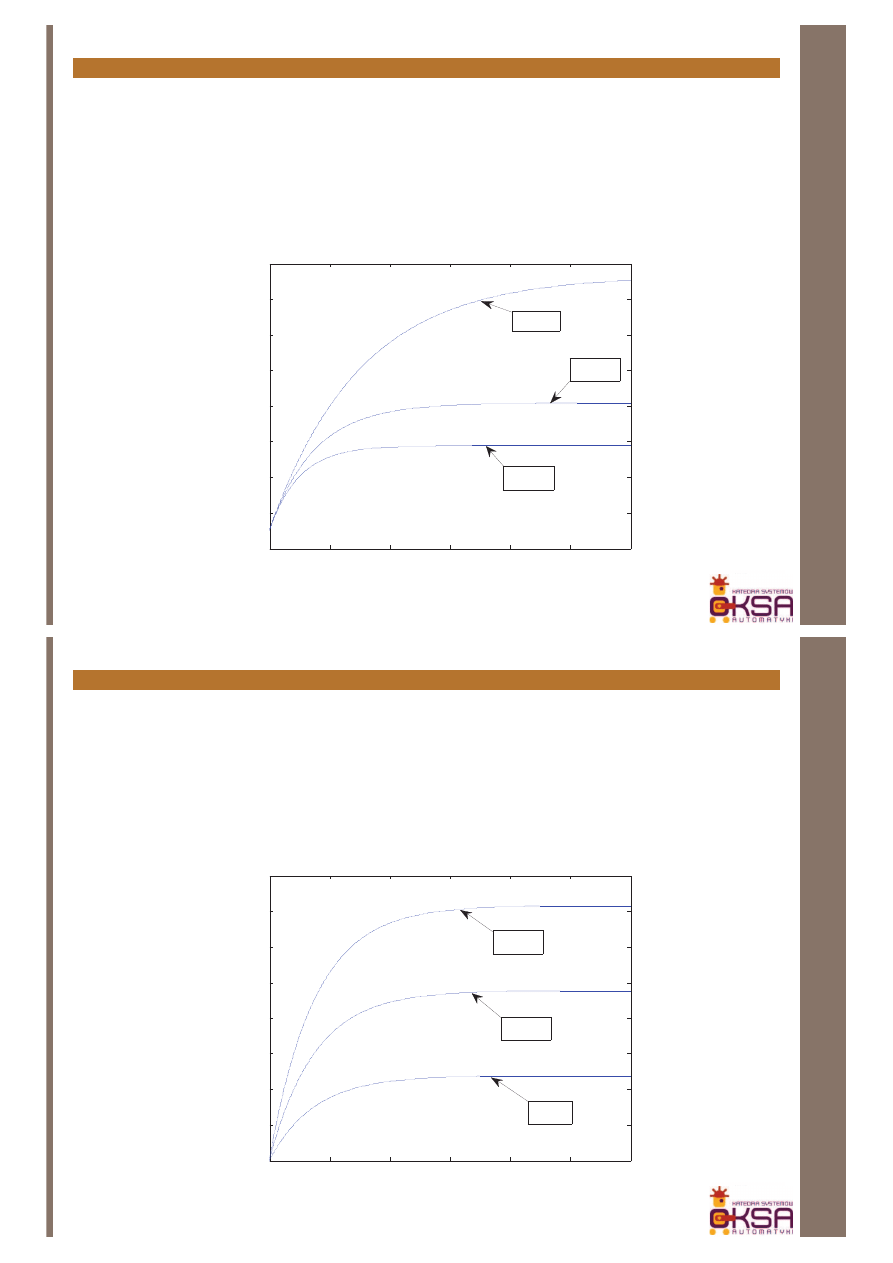
Zauważmy, że konstruktor urządzenia znając jego model matematyczny może
określić na podstawie wymagań użytkownika parametry techniczne
urządzenia np. szybkość z jaką ma nastąpić ogrzanie wody. W przykładzie
poniżej mamy wykresy dla trzech różnych objętości komór zawierających
grzałkę (zakładamy stałą moc (15kW) i stały pobór wody (6l/min))
0
2
4
6
8
10
12
15
20
25
30
35
40
45
50
55
t [s]
T
(t
)
[°
C
]
V=100ml
V=150ml
V=250ml
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
71
Inżynieria systemów dynamicznych
Można również sprawdzić jak zmieni się zachowanie ogrzewacza w
zależności od poboru wody
0
2
4
6
8
10
12
10
20
30
40
50
60
70
80
90
t [s]
T
(t
)
[°
C
]
3l/min
6l/min
9l/min
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
72
Inżynieria systemów dynamicznych
Można również sprawdzić jak zmieni się zachowanie ogrzewacza w
zależności od mocy grzałki
0
2
4
6
8
10
12
15
20
25
30
35
40
45
50
55
t [s]
T
(t
)
[°
C
]
15kW
10kW
5kW

M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
73
Inżynieria systemów dynamicznych
Z przykładu możemy wysnuć kilka wniosków:
-zmiana pojemności komory grzałki powoduje zmianę współczynników
równania różniczkowego, jednak dla określonej konstrukcji pojemność komory
jest stała
-zmiana natężenia przepływu powoduje zmianę współczynników równania
różniczkowego i może być traktowana jako zakłócenie zmieniające model
obiektu
-zmiana temperatury cieczy na wlocie do ogrzewacza nie wpływa na
współczynniki równania ale stanowi zakłócenie
-moc grzałki jest zwykle wielkością wejściową i zmieniając ją możemy wpłynąć
na temperaturę na wyjściu ogrzewacza
Jak widzimy, mimo że model jest stosunkowo prosty, jeśli chcemy uzyskać
stabilną temperaturę na wylocie ogrzewacza będziemy musieli wziąć pod
uwagę wiele czynników. Ale o tym za kilka tygodni...
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
74
Inżynieria systemów dynamicznych
Przykład:
Dany jest budynek o kubaturze V, sumie powierzchni przegród (ścian i sufitu)
S oraz idealnie zaizolowanej podłodze. Znając pojemność cieplną przegród
C
PRZ
, ich powierzchnię S oraz współczynnik wnikania
α
wyznaczyć przebieg
temperatury powietrza wewnątrz budynku w odpowiedzi na dobowe zmiany
temperatury zewnętrznej zamodelowane jako sygnał sinusoidalny o wartości
średniej 15°C oraz amplitudzie 5°C. W rozważaniach pominąć wpływ
nasłonecznienia oraz wymiany ciepła przez system wentylacji. Założyć, że
temperatura jest stała w całej objętości przegrody. Pojemność cieplna
powietrza zawartego w pomieszczeniu wynosi C.
(
)
t
t
T
t
T
S
dT
C
P
Z
P
PRZ
d
)
(
)
(
-
=
a
T
Z
(t)
T(t)
T
P
(t)
(
)
t
t
T
t
T
S
CdT
P
d
)
(
)
(
-
=
a

M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
75
Inżynieria systemów dynamicznych
Równania stanu:
T
Z
(t)
T(t)
T
P
(t)
)
(
0
)
(
)
(
0
d
d
d
d
t
T
a
t
T
t
T
b
b
a
t
T
t
T
Z
P
P
ú
û
ù
ê
ë
é
+
ú
û
ù
ê
ë
é
ú
û
ù
ê
ë
é
-
-
=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Modelowanie układów nieelektrycznych – układy systemy termiczne
76
Inżynieria systemów dynamicznych
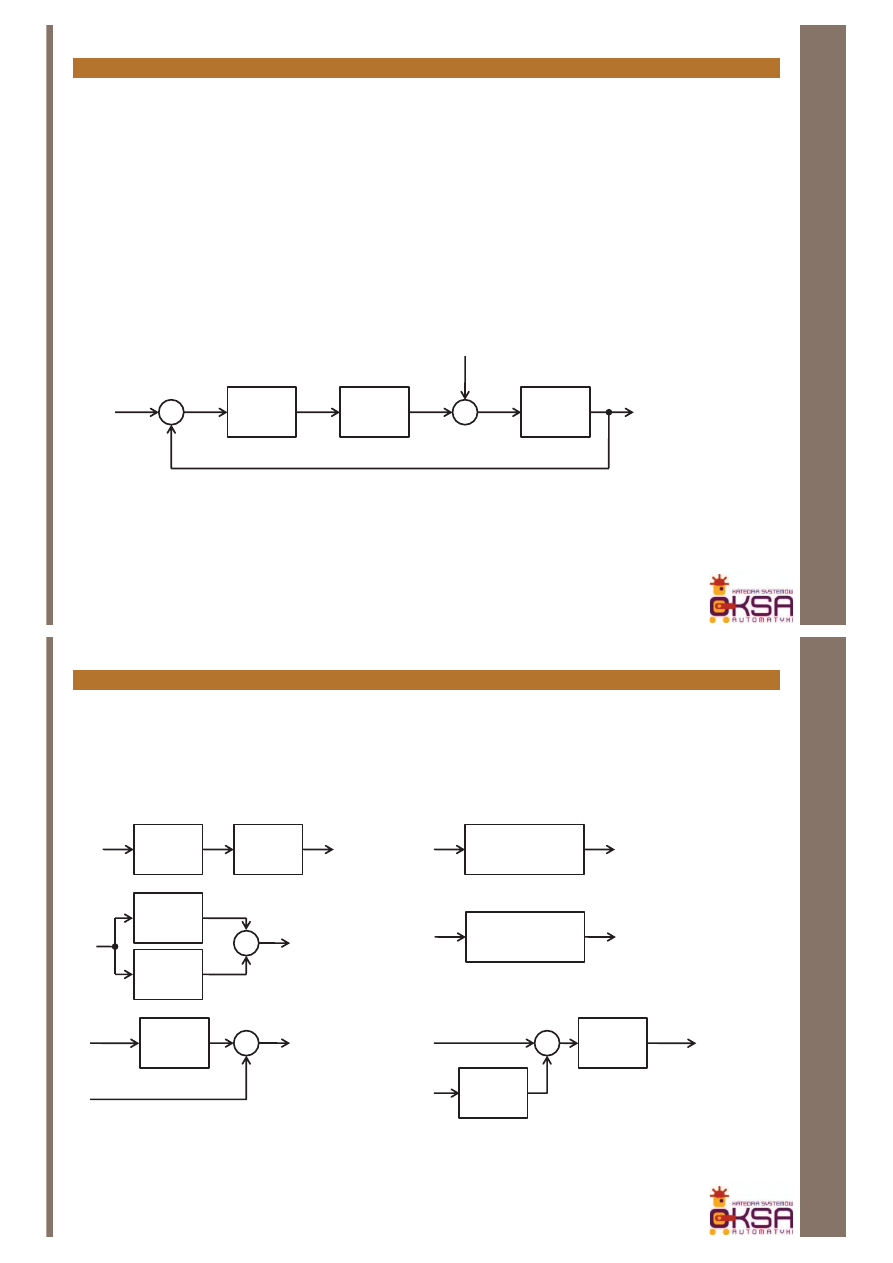
Przykładowe przebiegi (parametry w kodzie
źródłowym)
50
60
70
80
90
100
110
120
10
12
14
16
18
20
te
m
p
e
ra
tu
ra
[
°C
]
Czas [h]
Tz
T
clear
all
; close
all
; clc;
aa =10;
% m - szerokoϾ
bb = 10;
% m - d³ugoœæ
hh= 3;
% m РwysokoϾ
S=2*(aa+bb)*hh+aa*bb
% powierzchnia œcian
alfa= 2.5;
% W/(m2K) wspó³czynnik wnikania
ro_c = 1700;
% kg/m3 - gêstoœæ przegrody
Cwl_prz = 900;
% J/(kg*K) - ciep³o w³aœciwe
przegrody
d = 0.15;
% m - przekrój przegrody
Cp=(2*(aa+bb)*hh +aa*bb) *d * ro_c *Cwl_prz;
%pojemnoœæ cieplna œciany
ro_p = 1.3;
% kg/m3 - gêstoœæ powietrza
Cwl_pow = 1005
% J/(kg*K) - ciep³o w³aœciwe
powietrza
CC=aa*bb*hh*1300;
%pojemnoϾ cieplna
powietrza w pomieszczeniu
a=alfa*S/Cp; b=alfa*S/CC
A=[-a 0; b -b];B=[a;0];C=[0 1];D=0;
t=0:10:5*24*60*60;
% obserwacje co 10s przez
5 dni
Tz=15+5*sin(2*pi*t/okres);
% temp.
zewnêtrzna
T=lsim(ss(A,B,C,D),Tz,t,[15;15]);
plot(t/3600,Tz);
hold
on
;
plot(t/3600,T,
'k:'
);
axis([48,120, 9,21]);
% interesuje nas stan
ustalony wiêc 'obcinamy’ wyniki
ylabel(
'temperatura [°C]'
);
xlabel(
'Czas [h]'
);
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Schematy blokowe
W przypadku modelowania złożonych układów wygodnie jest podzielić je na
pewne prostsze elementy funkcjonalne.
Aby stworzyć schemat blokowy należy:
•podzielić system na elementy funkcjonalne
•zrozumieć i opisać poszczególne elementy funkcjonalne
•zrozumieć i opisać powiązania pomiędzy elementami funkcjonalnymi
systemu
77
Inżynieria systemów dynamicznych
masa
pojazdu
silnik
regulator
v(t)
-prędkość pojazdu
-prędkość zadana
-siła napędzająca pojazd (wynika z momentu na wale silnika)
-wychylenie przepustnicy
-uchyb sterowania
-zakłócenia (np. wynikające ze zmiany nachylenia drogi)
v
R
(t)
u(t)
f(t)
_
v(t)
v
R
(t)
f(t)
u(t)
e(t)
z(t)
e(t)
z(t)
Przykład (bardzo uproszczony): tempomat w samochodzie
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
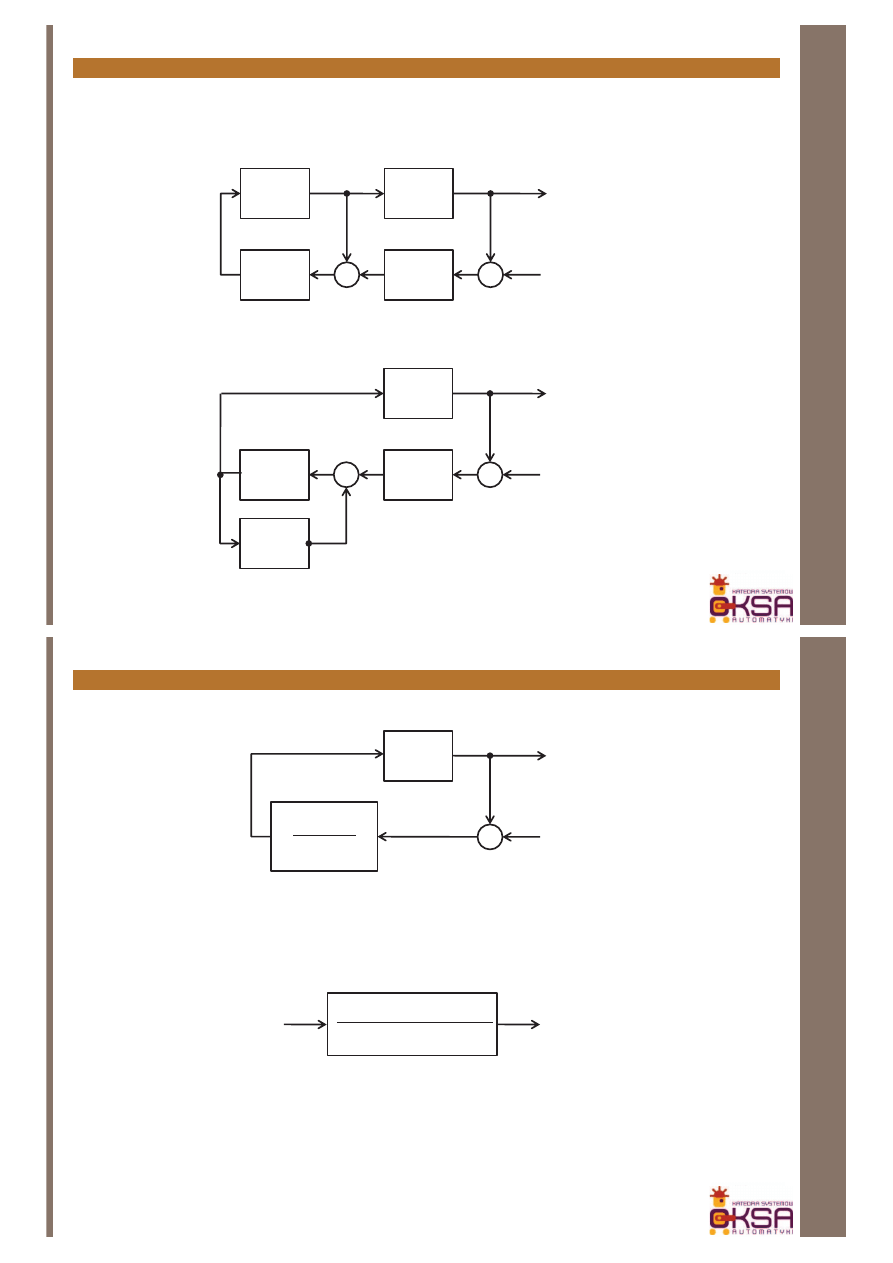
Schematy blokowe
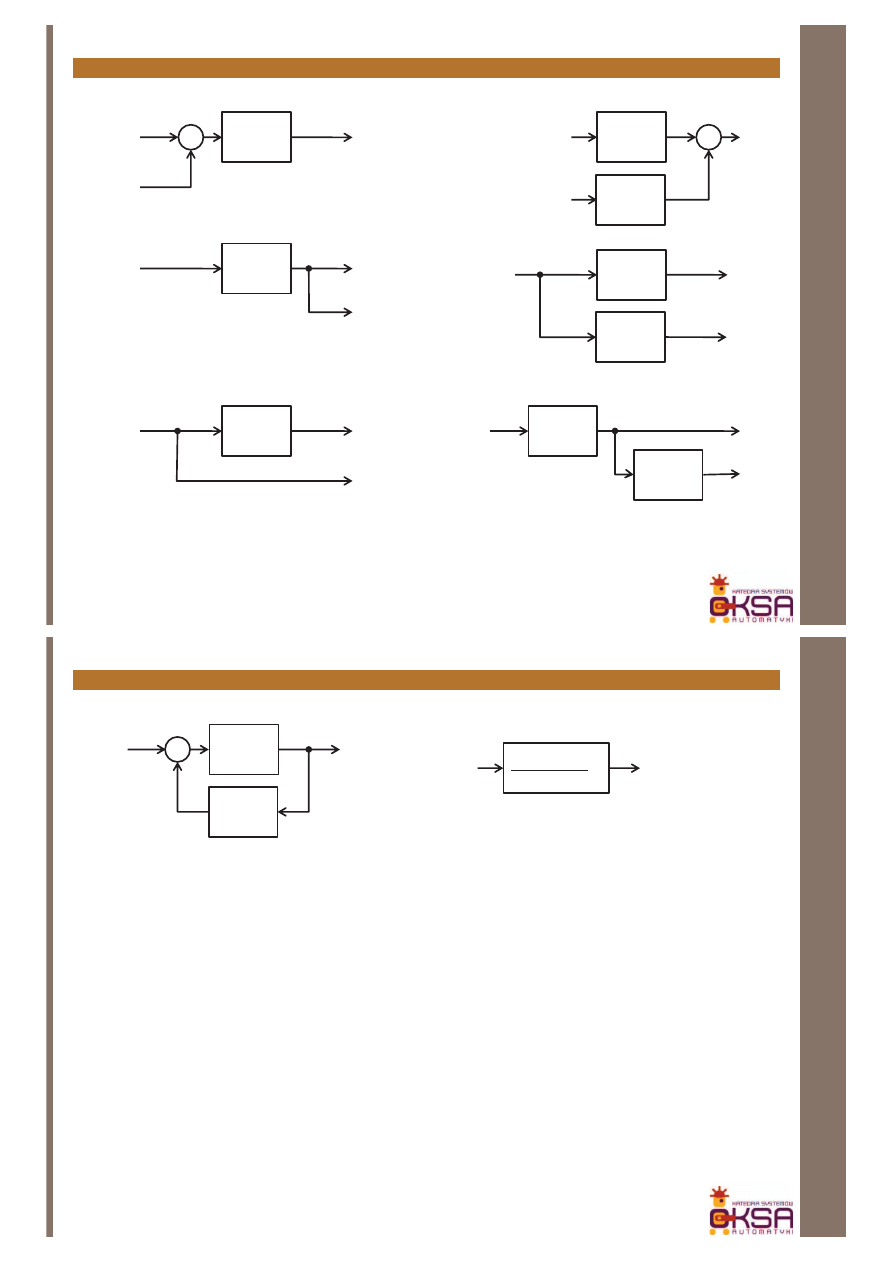
W przypadku, gdy poszczególne elementy funkcjonalne mogą być opisane
transmitancjami, możemy poszukiwać transmitancji całego układu korzystając
z zasad przekształcania schematów blokowych
G
1
(s)
G
2
(s)
G
1
(s)
G
2
(s)
G
1
(s) +G
2
(s)
78
Inżynieria systemów dynamicznych
G
1
(s)
1/G(s)
G(s)
G
1
(s) G
2
(s)
=
=
=
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Schematy blokowe
79
Inżynieria systemów dynamicznych
G(s)
G(s)
G(s)
G(s)
G(s)
G(s)
G(s)
G(s)
1/G(s)
=
=
=
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Schematy blokowe
80
Inżynieria systemów dynamicznych
G(s)
H(s)
G(s)H(s)
1
G(s)
±
-
+
=
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
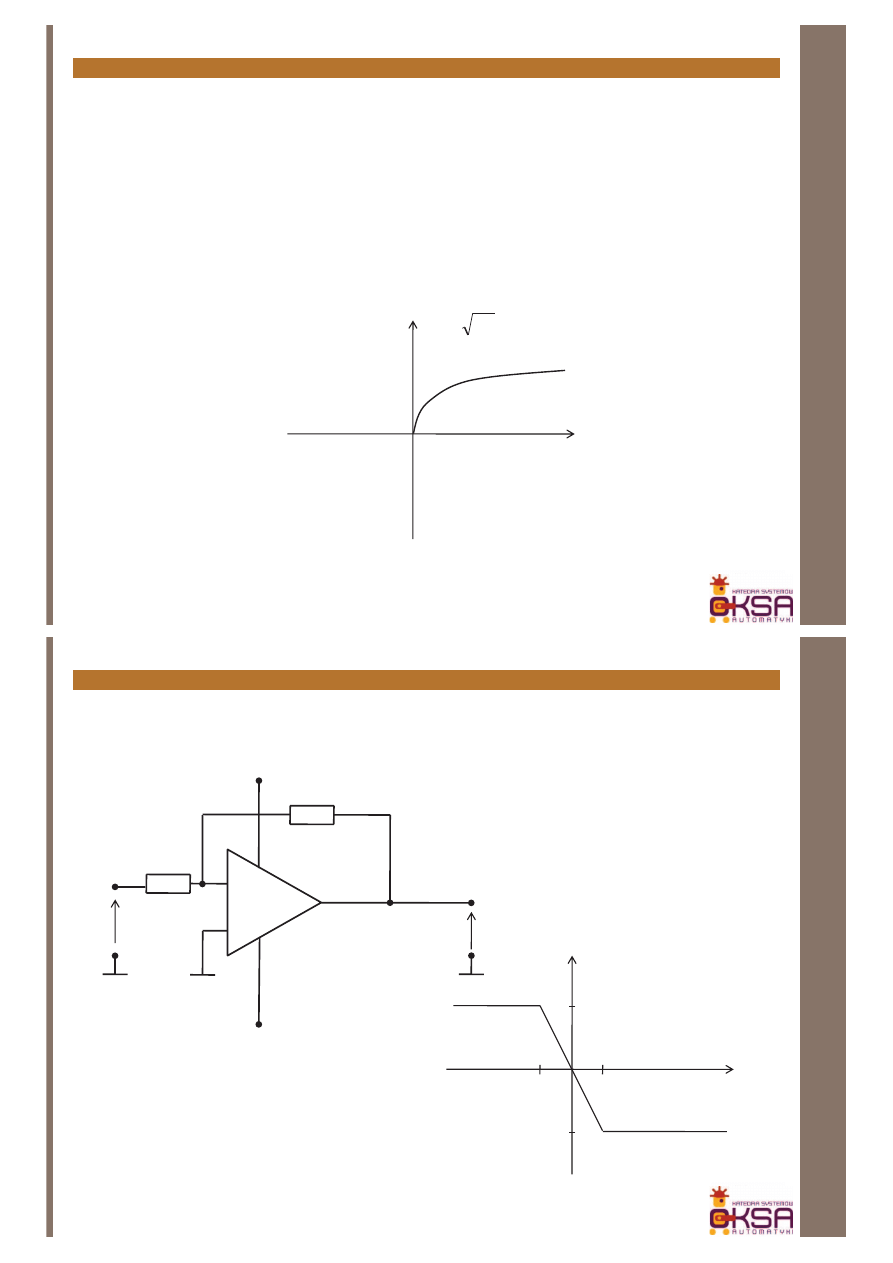
Schematy blokowe - przykład
81
Inżynieria systemów dynamicznych
G
1
G
2
H
1
H
2
R
Y
Przykład:
Wyznaczyć transmitancję Y/R w poniższym układzie regulacji kaskadowej (dla
poprawienia czytelności rezygnujemy z pokazywania zależności od „s”)
_
_
G
1
G
1
G
2
H
1
H
2
R
Y
_
_
Rozwiązanie:
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Schematy blokowe - przykład
82
Inżynieria systemów dynamicznych
G
1
G
2
R
Y
_
2
1
2
1
H
G
1
H
H
+
2
1
2
1
2
1
2
1
2
1
H
H
G
G
H
G
1
H
H
G
G
+
+
R
Y
Uwaga: Wypadkową transmitancję można również wyznaczyć stosując
regułę Masona
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Układy nieliniowe
83
Inżynieria systemów dynamicznych
Niestety świat jest liniowy tylko w ograniczonym zakresie...
Przyczyny nieliniowości(I)
-zjawiska fizyczne związane z konstrukcją elementów (np. zależność
indukcyjności cewki z rdzeniem od prądu, charakterystyki elementów
półprzewodnikowych, tarcie lub luzy w układach mechanicznych, opory
przepływu dla przepływów burzliwych w hydraulice)
Δp
charakterystyka zaworu
p
k
Q
D
=
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Układy nieliniowe
84
Inżynieria systemów dynamicznych
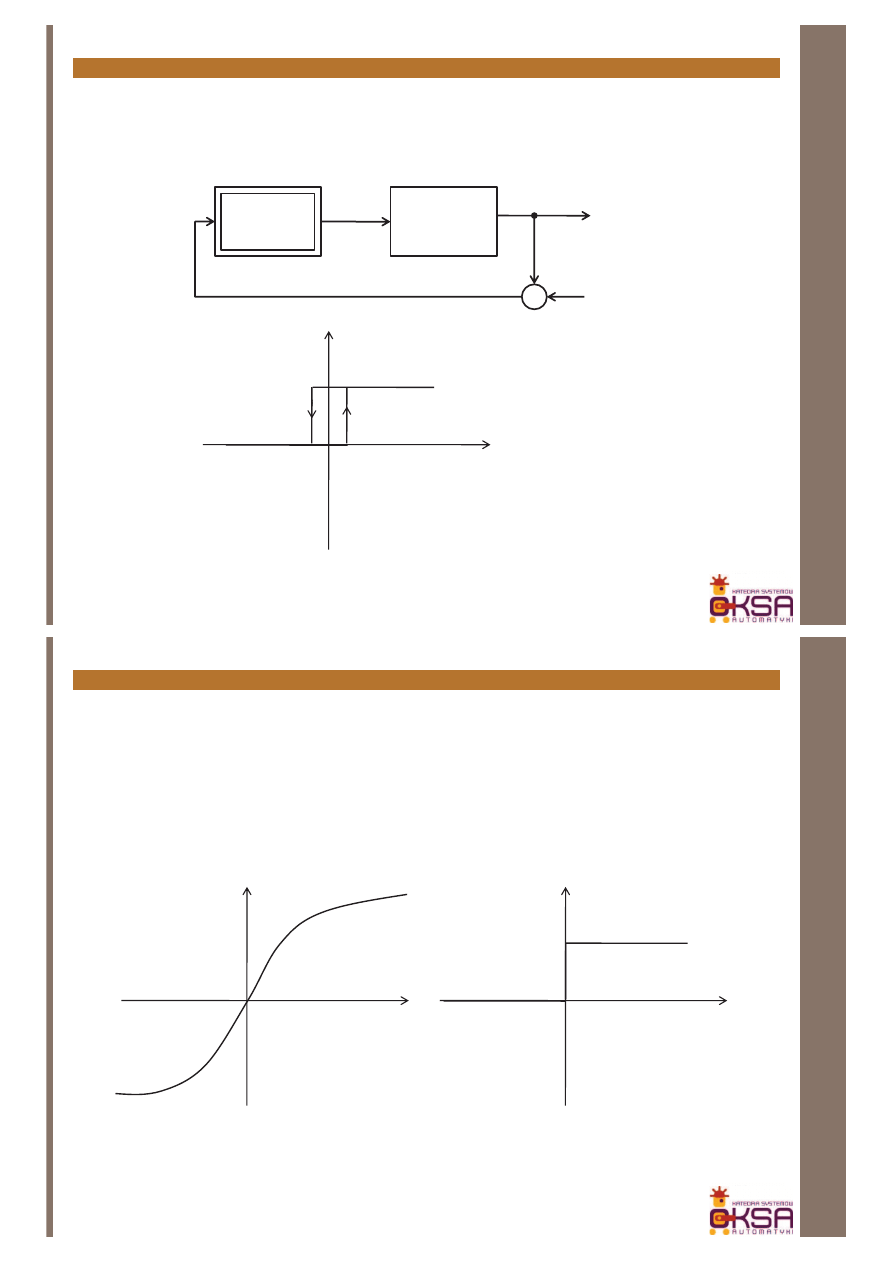
Przyczyny nieliniowości (II)
-ograniczenia związane z dostarczaniem energii do układów
U
1
+
_
U
2
4R
R
10V
-10V
U
1
U
2
2,5V
-2,5V
10V
-10V
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Układy nieliniowe
85
Inżynieria systemów dynamicznych
Przyczyny nieliniowości:
-specyfika regulatora (np. termostat)
Grzejnik
R
Y
_
e
U=f(e)
e
U
f(e)
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Układy nieliniowe
86
Inżynieria systemów dynamicznych
Wszystkie rzeczywiste układy są w istocie nieliniowe, tak więc mówiąc o
układzie liniowym mamy na myśli model przybliżający działanie układu
fizycznego po linearyzacji. W wielu przypadkach linearyzacja taka jest
dozwolona pod warunkiem, że poruszamy się w pewnym obszarze pracy.
u
y
u
y
tu możemy posłużyć się metodą linearyzacji...
... a tu nie możemy

M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Układy nieliniowe
87
Inżynieria systemów dynamicznych
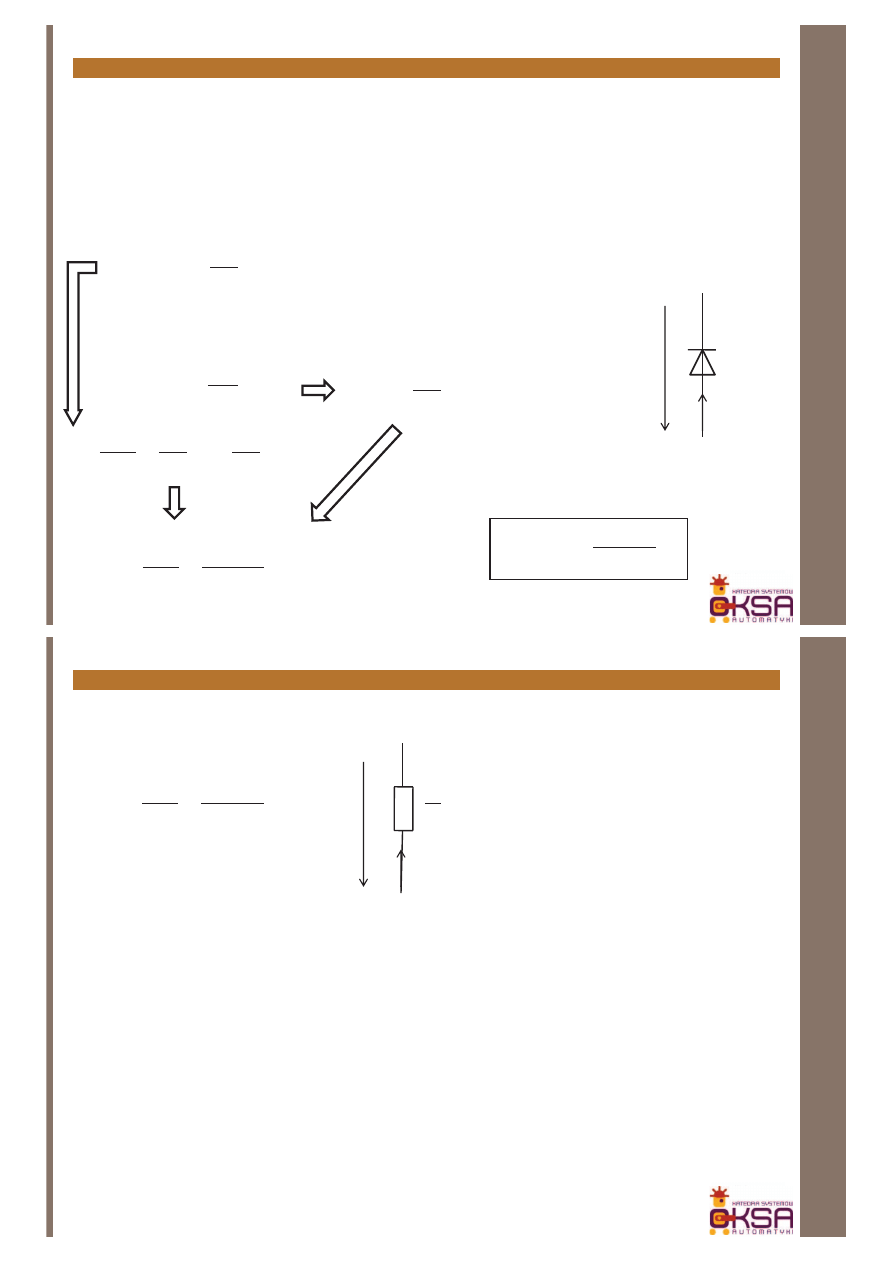
Załóżmy, że działanie pewnego obszaru możemy opisać funkcją f(x) oraz
załóżmy, że sygnał wejściowy układu ulega zaburzeniu, takiemu że
x=x
0
+Δx, gdzie x
0
to punkt pracy układu. Zaburzeniu temu towarzyszy
zmiana wartości sygnału wyjściowego f(x)
)
(
)
(
)
(
0
x
f
x
f
x
f
D
=
-
x
x
f
x
x
f
d
)
(
d
)
(
»
D
D
x
x
x
f
x
f
x
x
D
»
D
=
0
d
)
(
d
)
(
x
f(x)
x
0
f(x
0
)
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Układy nieliniowe
88
Inżynieria systemów dynamicznych
Ściślejszym uzasadnieniem metody jest rozwinięcie funkcji f(x) w szereg
Taylora
L
+
D
+
D
+
=
=
=
!
2
)
(
)
(
)
(
)
(
2
2
2
0
0
0
x
dx
x
f
d
x
dx
x
df
x
f
x
f
x
x
x
x
x
dx
x
df
x
f
x
f
x
f
x
x
D
»
-
=
D
=
0
)
(
)
(
)
(
)
(
0
Modelem liniowym jest pierwszy człon rozwinięcia funkcji w szereg Taylora
Dokładność przybliżenia zależy od pozostałych członów tzn. od gładkości
funkcji oraz Δx.
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Układy nieliniowe
89
Inżynieria systemów dynamicznych
Przykład:
Załóżmy, że dana jest dioda półprzewodnikowa, przez którą w punkcie pracy
określonym przez napięcie na diodzie U
D
, płynie prąd I
D
. Należy znaleźć
jaka będzie w tym punkcie pracy odpowiedź (zmiana prądu Δi) na niewielkie
odchylenie napięcia (Δi) od punktu pracy
Prąd diody dany jest wzorem:
÷
÷
ø
ö
ç
ç
è
æ
-
÷÷
ø
ö
çç
è
æ
=
1
exp
T
D
S
D
U
U
I
I
÷
÷
ø
ö
ç
ç
è
æ
-
÷÷
ø
ö
çç
è
æ
=
1
exp
T
D
S
D
U
u
I
i
w punkcie pracy prąd wynosi
÷÷
ø
ö
çç
è
æ
=
T
D
T
S
D
D
U
u
U
I
u
i
exp
d
d
T
S
D
D
D
U
I
I
u
i
+
=
=
d
d
a
S
D
T
D
S
I
I
U
u
I
+
=
÷÷
ø
ö
çç
è
æ
exp
u
U
I
I
u
i
T
S
D
D
+
=
D
=
D
a
S
I
gdzie -prąd nasycenia, -potencjał termiczny
T
U
u
U
u
D
D
D
+
=
i
I
i
D
D
D
+
=
M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Układy nieliniowe
90
Inżynieria systemów dynamicznych
w rezultacie otrzymaliśmy tzw. model małosygnałowy diody
T
S
D
D
D
U
I
I
u
i
+
=
=
d
d
a
u
D
i
D
a
1
Więcej na temat wykorzystania omawianej metody do tworzenia modeli
małosygnałowych można znaleźć w skrypcie:
W. Stepowicz Elementy półprzewodnikowe i układy scalone, Skrypt PG

M
E
T
O
D
Y
O
P
IS
U
U
K
Ł
A
D
Ó
W
Układy nieliniowe
91
Inne metody analizy układów nieliniowych (poza programem przedmiotu):
-metoda płaszczyzny fazowej
-metoda funkcji opisującej
Literatura
J. Nowakowski Podstawy Automatyki tom 2, Skrypt PG
Wyszukiwarka
Podobne podstrony:
INSTRUKCJA OBSŁUGI DEKODER SAGEM ISD 4285 PL
fpr-wyk3, FIR UE Katowice, SEMESTR IV, Finanse przedsiębiorstw, Finanse Przedsiębiorstwa
Fot wyk3 int
mb-wyk3, UE Katowice FiR, marketing bankowy
gitg-wyk3, FIR UE Katowice, SEMESTR VI, gieldy, gieldy 1, gieldy
Ceny usług turystycznych wyk3, Geografia 2 rok, Ekonomiczne podstawy turystyki, Wykłady
isd cwiczenia
wyk3, studia, semestr V, zarzadzanie produkcja i uslugami, Wykład
Iinstrukcja Sagem ISD 83
et-wyk3, Logistyka, rok2, ekonomika transportu, ek
IB wyk3 09 www
Informatyka w turystyce wyk3 Bazarnik
di-wyk3
Wykład, mi-wyk3
WYK3, Y'=*cos(*t)
więcej podobnych podstron