A. Zaborski, Belka na podło u spr ystym – belki półniesko czone
Belki półniesko czone
Wzory
Całka ogólna równania belki półniesko czonej ma posta :
)
cos
sin
(
)
(
)
(
ξ
ξ
ξ
ξ
ξ
B
A
e
w
w
s
+
+
=
−
,
wi c za ka dym razem nale y wyznaczy 2 stałe całkowania oraz całk szczególn . Całk
szczególn mo na wyznaczy – jak w przypadku belki niesko czonej długo ci – metod
przewidywania. Stałe całkowania wyznaczamy albo z kinematycznych warunków
brzegowych (je li istniej ) albo ze statycznych warunków brzegowych:
)
('
''
)
(
),
('
'
)
(
3
2
ξ
α
ξ
ξ
α
ξ
EJw
Q
EJw
M
−
=
−
=
.
Poni ej kilka przykładów zastosowania warunków brzegowych i uzyskiwanych rozwi za
belek.
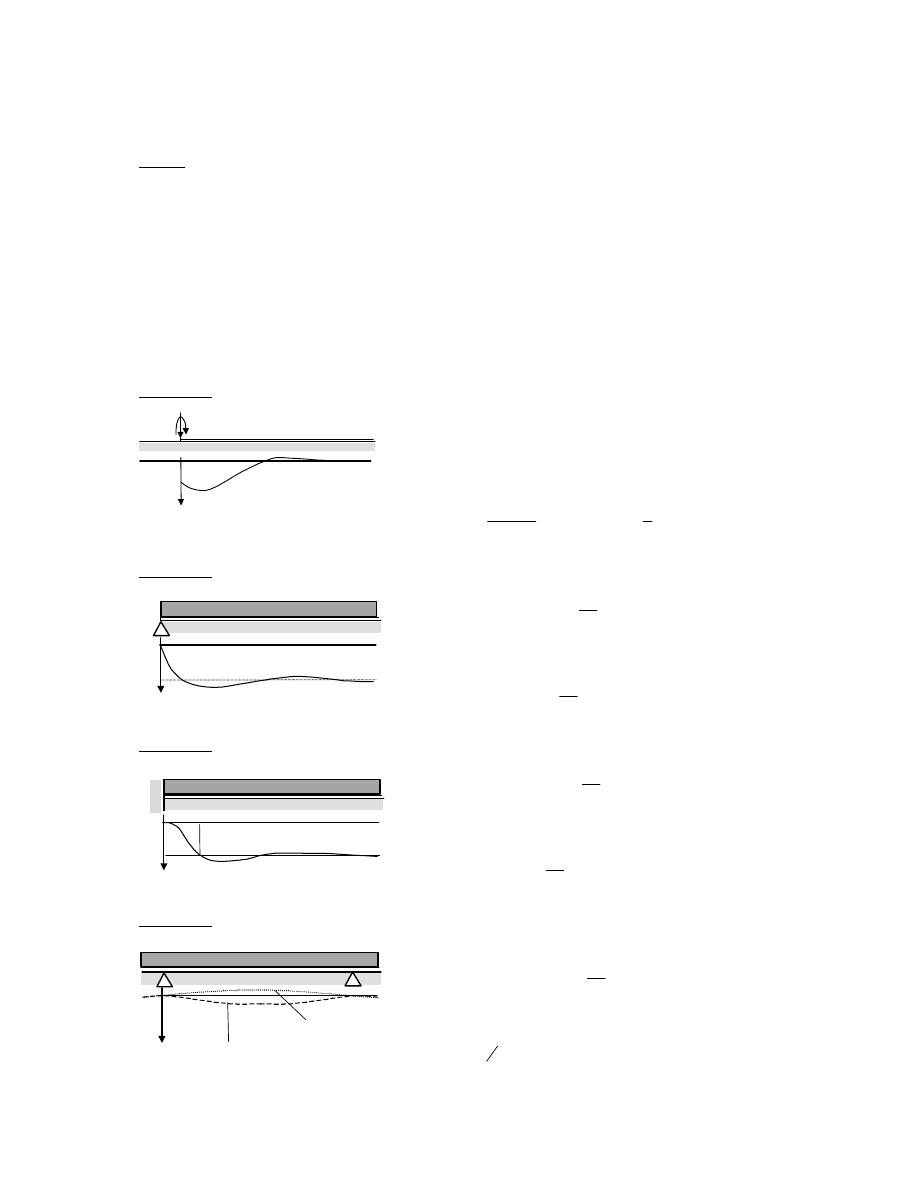
Przykład 1
całka szczególna
0
)
(
=
ξ
s
w
z warunków brzegowych:
P
Q
M
M
−
=
=
+
)
0
(
,
)
0
(
0
otrzymujemy:
(
)
[
]
ξ
ξ
α
ξ
α
ξ
cos
sin
2
1
)
(
0
0
2
M
M
e
EJ
w
P
−
+
=
−
Przykład 2
całka szczególna
bc
q
w
s
=
)
(
ξ
z warunków brzegowych:
0
)
0
(
)
0
(
=
= M
w
otrzymujemy:
(
)
ξ
ξ
ξ
cos
1
)
(
−
−
=
e
bc
q
w
Przykład 3
całka szczególna
bc
q
w
s
=
)
(
ξ
z kinematycznych warunków brzegowych:
0
)
0
('
)
0
(
=
= w
w
otrzymujemy:
(
)
[
]
ξ
ξ
ξ
ξ
sin
cos
1
)
(
+
−
=
−
e
bc
q
w
.
Przykład 4
m - bezwymiarowa odległo mi dzy podporami
całka szczególna
bc
q
w
s
=
)
(
ξ
z warunków brzegowych:
0
)
(
)
0
(
=
= m
w
w
, albo dla symetrii rozwi zania:
0
)
(
)
0
('
2
=
=
m
w
w
otrzymujemy warto ci reakcji na
podporach:
P
Mo
w
w
0
q
w
w
0
q
w
3/4
π
w
m > 3/4
π
m < 4/3
π

A. Zaborski, Belka na podło u spr ystym – belki półniesko czone
(
)
m
m
e
q
P
m
sin
cos
1
1
2
+
+
⋅
=
−
α
Wykresy ugi zale od bezwymiarowej odległo ci mi dzy podporami. Odległo ta jest nie
tylko funkcj odległo ci fizycznej ale i współczynnika
α, który z kolei jest stosunkiem
współczynnika podatno ci podło a, c, i sztywno ci zginania belki, EJ.
Wyszukiwarka
Podobne podstrony:
Belki półnieskończone
04 18 belki i ramy zadanie 18id Nieznany (2)
belki A0
AS Projektowanie swobodnie podpartej belki zespolonejczęste
04 05 belki i ramy zadanie 05id 4920
04 16 belki i ramy zadanie 16id 4940
belki proste zadania z rozwiaza Nieznany (2)
Belki rozwiązania
10 RÓW OSI UG BELKI
04 08 belki i ramy zadanie 08id 4924
Belki Układ1
Mathcad Projekt belki kablobetonowej
LABORATORIUM 4 badanie belki zelbetowej
Badanie odksztalcen belki zginanej metoda tensometrii oporowej
Belki proste Siły wewnętrzne 3
belki(1)
# Projekt nr 1 TEMAT Wyznaczenie linii ugięcia belki
Belki ramy, 21, 1
więcej podobnych podstron