PROJEKT BELKI KABLOBETONOWEJ
1. Założenia do projektu
Rozpiętość belki w osiach podpór
L
25.0m
:=
Rozstaw osiowy belek
b
9.0m
:=
Sposób użytkowania
sala sportowa
gdodatkowe
1.5
kN
m
2
:=
Obciążenie dodatkowe
Klasa betonu
C55/67
Rodzaj cementu
N
Stal sprężająca
sploty siedmiodrutowe Y 1860 S7
Klasa środowiska
XC3
Wilgotność względna środowiska
RH
60%
:=
t
0
21dni
:=
Wiek betonu w chwili sprężania
2. Charakterystyki materiałowe
2.1. Beton (BWW) - beton belki
fck
55MPa
:=
wytrzymałość charakterystyczna betonu na ściskanie
fcd
fck
1.5
36.667 MPa
=
:=
wytrzymałość obliczeniowa betonu na ściskanie
fck.cube
67MPa
:=
wytrzymałość gwarantowana na ściskanie
fcm
63MPa
:=
wytrzymałość średnia betonu na ściskanie
fctm
4.2MPa
:=
wytrzymałość średnia betonu na rozciąganie
Ecm
38GPa
:=
wartość średnia modułu sprężystości betonu
γb
25
kN
m
3
:=
ciężar objętościowy betonu
γC
1.4
:=
współczynnik (tab. NA.2 str. 4 EC2)
2.2. Beton C20/25 - beton nadbetonu
fck.n
20MPa
:=
wytrzymałość charakterystyczna betonu na ściskanie
fcd.n
fck.n
1.5
13.333 MPa
=
:=
wytrzymałość obliczeniowa betonu na ściskanie
fck.cube.n
25MPa
:=
wytrzymałość gwarantowana na ściskanie
5

fcm.n
28MPa
:=
wytrzymałość średnia betonu na ściskanie
fctm.n
.2MPa
:=
wytrzymałość średnia betonu na rozciąganie
Ecm.n
30GPa
:=
wartość średnia modułu sprężystości betonu
γb
25
kN
m
3
:=
ciężar objętościowy betonu
2.3. Stal sprężająca Y 1860 S7
Ap1.15.7
150mm
2
:=
powierzchnia splotu siedmiodrutowego
fpk
1860MPa
:=
charakterystyczna granica plastyczności stali
fp01k
0.9 fpk
1674.000 MPa
=
:=
Ep
190GPa
:=
γp
1.15
:=
współczynnik (tab. NA.2 str. 4 EC2)
fpd
fp01k
γp
1455.652 MPa
=
:=
2.4. Stal zwykła AIII RB500W
fyk
500MPa
:=
charakterystyczna granica plastyczności stali
fyd
420MPa
:=
obliczeniowa granica plastyczności stali
Es
200GPa
:=
moduł sprężystości stali
2.5. Parametry pomocnicze
t
0
21.000 dni
=
wiek betonu w chwili sprężania
s
0.25
:=
rodzaj cemntu - N
współczynnik zależny od klasy cementu (str. 24 EC2)
βcc t
( )
exp s 1
28dni
t
-
:=
współczynnik zależny od wieku betonu (wzór 3.2
str. 24 EC2)
βcc t
0
( )
0.962
=
współczynnik - wiek betonu t0
fcm t()
βcc t
( ) fcm
:=
wytrzymałość średnia betonu na ściskanie zależna od
wieku betonu (wzór 3.1 str. 24 EC2)
fcm.n t
( )
βcc t() fcm.n
:=
wytrzymałość średnia betonu na ściskanie zależna od
wieku betonu (wzór 3.1 str. 24 EC2)
fcm t
0
( )
60.610 MPa
=
wytrzymałość średnia betonu na ściskanie - wiek
betonu t0
fctm t
( )
βcc t
( ) fctm
:=
wytrzymałość średnia betonu na rozciąganie zależna
od wieku betonu (wzór 3.1 str. 24 EC2)
fctm t
0
( )
4.041 MPa
=
wytrzymałość średnia betonu na rozciąganie - wiek
betonu t0
6

Ecm t
( )
fcm t
( )
fcm 28dni
(
)
0.3
Ecm
:=
wartość średnia modułu sprężystości betonu zależna
od wieku betnu (wzór 3.5 str.25 EC2)
Ecm t
0
( )
37.562 GPa
=
wartość średnia modułu sprężystości betonu - wiek
betonu t0
Ecm.n t()
fcm.n t()
fcm.n 28dni
(
)
0.3
Ecm.n
:=
wartość średnia modułu sprężystości nadbetonu
zależna od wieku betnu (wzór 3.5 str.25 EC2)
3. Wstępne zestawienie obciążeń
3.1. Ciężar płyt stropowych
Przyjęto płyty HC265 firmy Consolis
gstrop
3.8
kN
m
2
:=
ciężar własny płyty stropowej
hHC265
265mm
:=
wysokość płyty stropowej
3.2. Obciążenia stałe dodatkowe
gdodatkowe 1.500
kN
m
2
=
obciążenie stałe dodatkowe
3.3. Obciążenia zmienne
3.3.1. Obciążenia zmienne użytkowe normalne
Sala sportowa - powierzchnia ogólno
dostępna - -> kategoria C5
(tab. 6.1 str. 16 EC1)
q
5.0
kN
m
2
:=
obciążenie użytkowe - wartość zalecana
(tab. 6.2 str.17 EC1)
3.3.2. Obciążenia zmienne użytkowe - robotnicy
gr
3
kN
m
2
:=
obciążenie robotnikami
3.4. Ciężar własny belki
3.4.1. Przyjęcie wstępne wysokości belki
leff
L
25.000 m
=
:=
rozpiętość belki
0.04 leff
1.000 m
=
minimalna zalecana wysokość belki
0.06 leff
1.500 m
=
maksymalna zalecana wysokość belki
7

Przyjęto
hb
1.80m
:=
wstępna przyjęta wysokość belki
3.4.2. Cieżar własny belki
gbelki
γb 0.22
hb
2
17.820
kN
m
=
:=
ciężar własny belki na 1mb - obc. charakterystyczne
3.5. Kombinacja obciążeń
3.5.1. Współczynniki
γGjsup
1.35
:=
współczynnik częściowy dla oddziaływania stałego -
górna wartość obliczeniowa (tab. A 1.2B str.40 EC0)
γGjinf
1.00
:=
współczynnik częściowy dla oddziaływania stałego -
dolna wartość obliczeniowa (tab. A 1.2B str.40 EC0)
γQ1
1.5
:=
współczynnik częściowy dla oddziaływania
zmiennego - dolna wartość obliczeniowa (tab. A 1.2B
str.40 EC0)
ψ0
0.7
:=
współczynnik dla wartości kombinacyjnej
oddziaływania zmiennego (tab. A 1.1 str.38 EC0)
ψ1
0.7
:=
współczynnik dla wartości częstej oddziaływania
zmiennego (tab. A 1.1 str.38 EC0)
ψ2
0.6
:=
współczynnik dla wartości prawie stałej oddziaływania
zmiennego (tab. A 1.1 str.38 EC0)
ξ
0.85
:=
współczynnik redukcyjny dla niekorzystnych
oddziaływań stałych G (tab. A 1.2B str.40 EC0)
3.5.2. Kombinacja obciażeń dla stanów granicznych STR i GEO
Msd1
γGjsup gbelki gdodatkowe b
+
gstrop b
+
(
)
γQ1 ψ0
q
b
+
leff
2
8
1.060
10
4
kNm
=
:=
Msd2
γGjsup gbelki gdodatkowe b
+
gstrop b
+
(
)
γQ1 q
b
+
leff
2
8
1.218
10
4
kNm
=
:=
Msd
max Msd1 Msd2
,
(
)
1.218
10
4
kNm
=
:=
3.6. Sprawdzenie przyjętej wysokości belki
hmin
2.2
3
Msd
fcd
1.524 m
=
:=
wysokość minimalna
hmax
2.6
3
Msd
fcd
1.801 m
=
:=
wysokość maksymalna
8

hb hmin
1.000
=
warunek spełniony
hb hmax
1.000
=
warunek spełniony
4. Przyjęcie otuliny nominalnej zbrojenia zwykłego i kabli
4.1. Otulina minimalna
ϕosłonki
60mm
:=
średnica osłonki splotów
cmin.b
ϕosłonki
:=
minimalne otulenie ze względu na przyczepność
(tab 4.2 str. 45 EC2)
cmin.dur1
45mm
:=
minimalne otulenie ze względu na warunki środowiska
stali sprężającej (tab 4.5N str. 45 EC2)
cmin.dur2
35mm
:=
minimalne otulenie ze względu na warunki środowiska
stali zwykłej (tab 4.4N str. 45 EC2)
Δcdur.γ
0mm
:=
składnik dodatkowy ze względu na bezpieczeństwo
(punkt 4.4.1.2(6) str. 46 EC2)
Δcdur.st
0mm
:=
składnik dodatkowy ze względu na bezpieczeństwo
(punkt 4.4.1.2(7) str. 46 EC2)
Δcdur.add
0mm
:=
składnik dodatkowy ze względu na bezpieczeństwo
(punkt 4.4.1.2(8) str. 46 EC2)
cmin1
max cmin.b cmin.dur1 Δcdur.γ
+
Δcdur.st
-
Δcdur.add
-
,
10mm
,
(
)
60.000 mm
=
:=
cmin2
max cmin.dur2 Δcdur.γ
+
Δcdur.st
-
Δcdur.add
-
10mm
,
(
)
35.000 mm
=
:=
4.2. Dodatek ze względu na odchyłkę
Δcdev
5mm
:=
dodatek ze względu na odchyłkę
(punkt 4.4.1.3(3) str. 47 EC2)
4.3. Otulina nominalna
cnom1
cmin1 Δcdev
+
6.500 cm
=
:=
otulina dla stali sprężjącej
cnom2
cmin2 Δcdev
+
4.000 cm
=
:=
otulina dla stali zwykłej
5. Przyjęcie wymiarów belki
Wymiary elementów minimalne
bwmin
0.10hb 0.180 m
=
:=
szerokość środnika
bwmin2
ϕosłonki 2 cnom1
+
0.190 m
=
:=
szerokość środnika
bfdmin
0.30hb 0.540 m
=
:=
szerokość półki dolnej
hfdmin
0.15hb 0.270 m
=
:=
wysokość półki dolnej
9

bfgmin
0.40 hb
0.720 m
=
:=
szerokość półki górnej
hfgmin
0.10hb 0.180 m
=
:=
wysokość półki górnej
Wymiary elementów maksymalne
bwmax
0.12hb 0.216 m
=
:=
szerokość środnika
bfdmax
0.60hb 1.080 m
=
:=
szerokość półki dolnej
hfdmax
0.20hb 0.360 m
=
:=
wysokość półki dolnej
bfgmax
0.80 hb
1.440 m
=
:=
szerokość półki górnej
hfgmax
0.15hb 0.270 m
=
:=
wysokość półki górnej
Przyjęto wymiary belki
bw
0.24m
:=
szerokość środnika
bfd
0.85m
:=
szerokość półki dolnej
hfd
0.30m
:=
wysokość półki dolnej
bfg
1.30m
:=
szerokość półki górnej
hfg
0.30m
:=
wysokość półki górnej
hśr
hb hfg
-
hfd
-
1.200 m
=
:=
wysokość środnika
hb
hśr hfd
+
hfg
+
1.800 m
=
:=
wysokość całkowita belki
Przekrój przęsłowy
10

6. Charakterysyki geometryczne przekroju betonowego
6.1. Powierzchania przekroju
UWAGA: Przekrój w połowie rozpiętości belki
Acg
hfg bfg
0.390 m
2
=
:=
powierzchnia półki górnej
Acd
hfd bfd
0.255 m
2
=
:=
powierzchnia półki dolnej
Aśr
hśr bw
0.288 m
2
=
:=
powierzchnia środnika
Acc
Acg Acd
+
Aśr
+
0.933 m
2
=
:=
powierzchnia przekroju
6.2. Moment statyczny przekoju
Scc
bfd hfd
hfd
2
bw hśr
hfd
hśr
2
+
+
hfg bfg
hfd hśr
+
hfg
2
+
+
0.941 m
3
=
:=
6.3. Środek ciężkości położenia
zcd
Scc
Acc
1.009 m
=
:=
odległość środka ciężkości przekroju od dolnej
krawędzi
zcg
hb zcd
-
0.791 m
=
:=
odległość środka ciężkości przekroju od górnej
krawędzi
6.4. Moment bezwładości przekroju względem środka cieżkości
Icpd
bfd hfd
3
12
bfd hfd
zcd
hfd
2
-
2
+
0.190 m
4
=
:=
moment bezwładności półki dolnej
Icśr
bw hśr
3
12
bw hśr
zcd hfd
-
hśr
2
-
2
+
0.038 m
4
=
:=
moment bezwładności środnika
Icpg
bfg hfg
3
12
bfg hfg
zcg
hfg
2
-
2
+
0.163 m
4
=
:=
moment bezwładności półki górnej
Icc
Icpd Icśr
+
Icpg
+
0.391 m
4
=
:=
moment bezwładności przekroju
6.4. Sprawdzenia warunków
gbelki
Acc γb
23.325
kN
m
=
:=
ciężar belki
β
Acc
hb
2
0.288
=
:=
wskaźnik tęgości
0.18
β
0.35
1.000
=
warunek spełniony
11
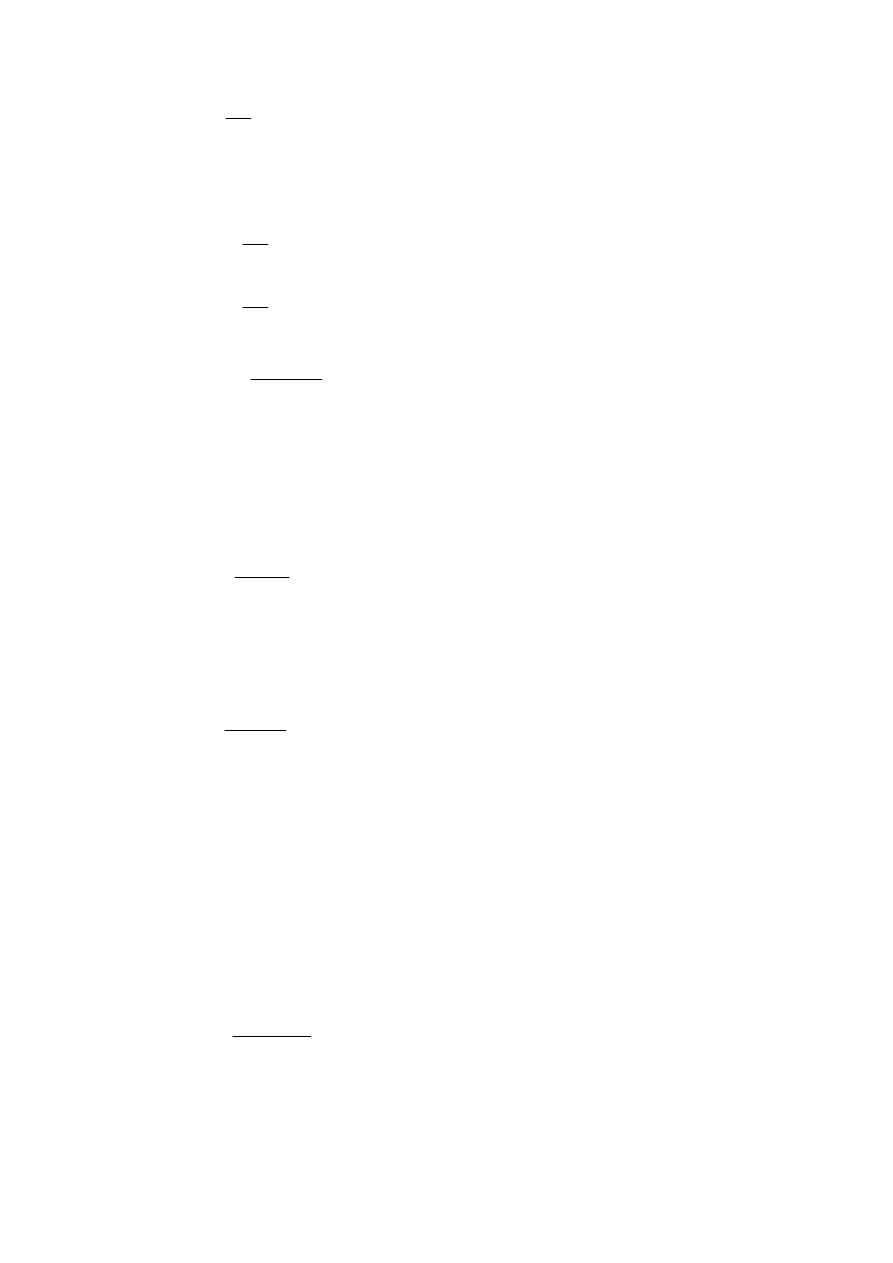
κ
zcd
hb
0.560
=
:=
wskaźnik asymetrii względem osi pionowej
0.35
κ
0.65
1.000
=
warunek spełniony
wcd
Icc
zcd
0.388 m
3
=
:=
wcg
Icc
zcg
0.494 m
3
=
:=
gwyd
wcd wcg
+
Acc hb
0.525
=
:=
wskaźnik wydajności
0.45
gwyd
0.55
1.000
=
warunek spełniony
7. Ustalenie wymaganej nośności cięgien i dobór ich liczby
z
0.85
:=
ramię sił wewnętrzych
Ap
Msd
z hb fpd
54.706 cm
2
=
:=
pole przekroju stali sprężającej
Ap1.15.7 150.000 mm
2
=
pole przekroju splotu siedmiodrutowego Y 1860 S7
7.1. Przyjęcie ilości splotów
n
Ap
Ap1.15.7
36.470
=
:=
nsplot
6 7
42.000
=
:=
przyjęto 6x7 splotów Y 1860 S7
nsplot n
1.000
=
warunek spełniony
8. Charakterysyki geometryczne przekroju sprowadzonego
8.1. Charakterystyki geometryczne przekroju w sytuacji początkowej
8.1.1. Powierzchania przekroju sprowadzonego
αs
Es
Ecm 28dni
(
)
5.263
=
:=
współczynnik wyrażający stosunek modułu
sprężystości stali zwykłej do modułu sprężystości
betonu belki
ϕ16
π 0.8cm
(
)
2
2.011 cm
2
=
:=
powierzchnia #16
As
14
ϕ16
28.149 cm
2
=
:=
powierzchnia zbrojenia belki stala zwykłą (#16)
12

Add
6
ϕosłonki
2
2
π
169.646 cm
2
=
:=
powierzchnia otworów na cięgna
Acs0
Acc
αs 1
-
(
)
As
+
Add
-
9280.356 cm
2
=
:=
8.1.2. Moment statyczny przekoju sprowadzonego
As
1
4
ϕ16
:=
As
2
4
ϕ16
:=
As
3
2
ϕ16
:=
As
4
2
ϕ16
:=
powierzchnia poszczególnych pasm zbrojenia
zwykłego
As
5
2
ϕ16
:=
As
6
2
ϕ16
:=
As
7
2
ϕ16
:=
As
8
2
ϕ16
:=
As
9
6
ϕ16
:=
As
10
6
ϕ16
:=
ds
1
6cm
:=
ds
2
24cm
:=
ds
3
44cm
:=
ds
4
64cm
:=
odległości środka ciężkości poszczególnych pasm
zbrojenie do krawędzi dolnej
ds
5
84cm
:=
ds
6
104cm
:=
ds
7
124cm
:=
ds
8
144cm
:=
ds
9
156cm
:=
ds
10
174cm
:=
Ad
1
3
ϕosłonki
2
2
π
:=
Ad
2
1
ϕosłonki
2
2
π
:=
powierzchnia poszczególnych pasm otworów
Ad
3
1
ϕosłonki
2
2
π
:=
Ad
4
1
ϕosłonki
2
2
π
:=
13

dd
1
10cm
:=
dd
2
23cm
:=
odległości środka ciężkości poszczególnych pasm
otworów do krawędzi dolnej
dd
3
36cm
:=
dd
4
49cm
:=
Scs0
Scc
1
10
i
αs 1
-
(
)
As
i
ds
i
(
)
=
+
1
4
i
Ad
i
dd
i
(
)
=
-
0.965 m
3
=
:=
8.1.3. Moment bezwładości przekroju sprowadzonego
zcs0
Scs0
Acs0
1.040 m
=
:=
położenie środka ciężkości od krawędzi dolnej belki
Ics0
Icc Acc zcd zcs0
-
(
)
2
+
1
10
i
αs 1
-
(
)
As
i
zcs0 ds
i
-
(
)
2
=
+
1
4
i
Ad
i
zcs0 dd
i
-
(
)
2
=
-
:=
Ics0 0.391 m
4
=
8.2. Charakterystyki geometryczne przekroju w sytuacji przejściowej
αp
Ep
Ecm 28dni
(
)
5.000
=
:=
współczynnik wyrażający stosunek modułu
sprężystości stali sprężającej do modułu
sprężystości betonu belki
8.2.1. Powierzchania przekroju sprowadzonego
Acsp
Acs0 Add
+
αp 1
-
(
)
Add
+
1.013 m
2
=
:=
8.2.2. Moment statyczny przekoju sprowadzonego
Ap
1
3 Ap1.15.7
:=
Ap
2
1 Ap1.15.7
:=
powierzchnia poszczególnych pasm stali
sprężającej
Ap
3
1 Ap1.15.7
:=
Ap
4
1 Ap1.15.7
:=
Scsp
Scs0
1
4
i
Ad
i
dd
i
(
)
=
+
αp 1
-
(
)
1
4
i
Ap
i
dd
i
(
)
=
+
0.969 m
3
=
:=
8.2.3. Moment bezwładości przekroju sprowadzonego
zcsp
Scsp
Acsp
0.957 m
=
:=
położenie środka ciężkości od krawędzi dolnej belki
Icsp
Ics0 Acs0 zcs0 zcsp
-
(
)
2
+
αp 1
-
(
)
1
3
i
Ap
i
zcsp dd
i
-
(
)
2
=
+
1
3
i
Ad
i
zcs0 dd
i
-
(
)
2
=
+
:=
14

Icsp 0.410 m
4
=
8.3. Charakterystyki geometryczne przekroju w sytuacji trwałej
Ecn
30GPa
:=
moduł sprężystości betonu (nadbetonu) C16/20
αcn
Ecn
Ecm 28dni
(
)
0.789
=
:=
współczynnik wyrażający stosunek modułu
sprężystości betonu (nadbetonu) do modułu
sprężystości betonu belki
8.3.1. Powierzchania przekroju sprowadzonego
bn
2 hHC265
0.530 m
=
:=
szerokość pasma nadbetonu
Acn
hHC265 bn
0.140 m
2
=
:=
powierzchnia nadbetonu (beton pomiędzy płytami
kanałowymi)
Acs
Acsp αcn Acn
+
1.124 m
2
=
:=
8.3.2. Moment statyczny przekoju sprowadzonego (względem środka ciężkości przekroju
belki)
hn
hHC265 265.000 mm
=
:=
wysokość nadbetonu
Scs
Scsp αcn Acn
hn
2
zcg
+
+
1.072 m
3
=
:=
8.3.3. Moment bezwładości przekroju sprowadzonego
zcs
Scs
Acs
0.954 m
=
:=
położenie środka ciężkości od krawędzi dolnej belki
Ics
Icsp Acsp zcsp zcs
-
(
)
2
+
αcn Acn
hn
2
hb
+
zcs
-
2
+
0.516 m
4
=
:=
9. Równianie równowagi sił
Approv
6 7
Ap1.15.7
63.000 cm
2
=
:=
powierzchnia przyjętych kabli sprężających
Acg
Approv fpd
fcd
2501.075 cm
2
=
:=
minimalna powierzchnia półki górnej
Acgprov
bfg hfg
3900.000 cm
2
=
:=
powierzchnia przyjętej półki górnej
Acg Acgprov
1.000
=
warunek spełniony
Acd
40 Approv
2520.000 cm
2
=
:=
minimalna powierzchnia półki dolnej
15

Acdprov
bfd hfd
2550.000 cm
2
=
:=
powierzchnia przyjętej półki dolnej
Acd Acdprov
1.000
=
warunek spełniony
10. Trasa kabla sprężającego
10.1. Minimalne odległości między kanałami
dg
32mm
:=
maksymalny wymiar ziarna kruszywa
Poziome
cw
max dg 5mm
+
ϕosłonki
,
50mm
,
(
)
60.000 mm
=
:=
(rys. 5.18 str. 134 EC2)
Pionowe
cv
max dg ϕosłonki
,
40mm
,
(
)
60.000 mm
=
:=
(rys. 5.18 str. 134 EC2)
10.2. Trasa paraboliczna o ogólnym równaniu
Przekrój przęsłowy
1
4
i
Ad
i
dd
i
(
)
=
3901.858 cm
3
=
moment statyczny osłonek względem dolnej krawędzi
belki
1
4
i
Ad
i
=
169.646 cm
2
=
powierzchnia osłonek
zosłonkiA
1
4
i
Ad
i
dd
i
(
)
=
1
4
i
Ad
i
=
0.230 m
=
:=
odległość środka cięzkości osłonek od dolnej
krawędzi belki
emax
zcs zosłonkiA
-
0.724 m
=
:=
Przekrój przypodporowy
dd
1
20cm
:=
dd
2
135cm
:=
odległości środka ciężkości poszczególnych pasm
otworów do krawędzi dolnej
dd
3
150cm
:=
dd
4
165cm
:=
16
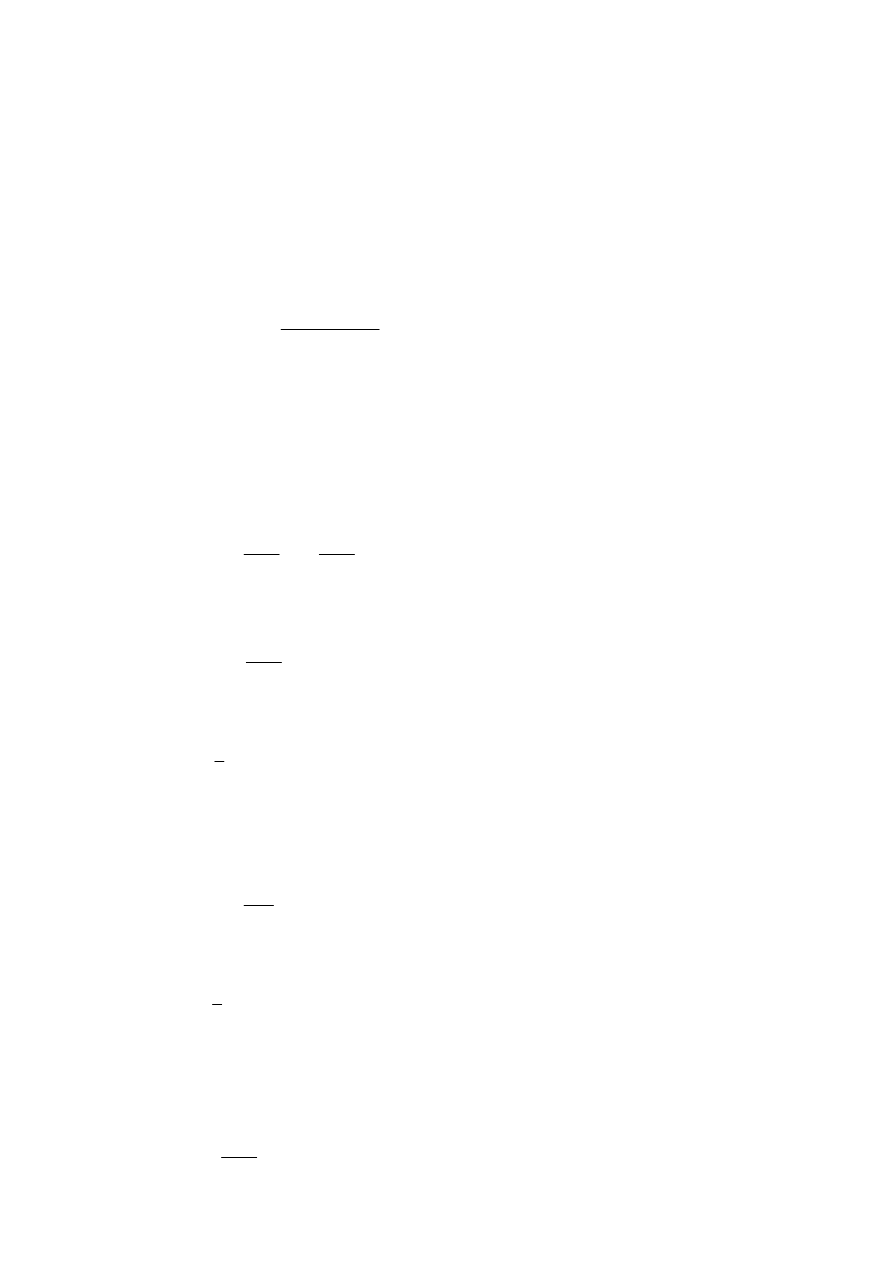
1
4
i
Ad
i
dd
i
(
)
=
1.442
10
4
cm
3
=
moment statyczny osłonek względem dolnej krawędzi
belki
1
4
i
Ad
i
=
169.646 cm
2
=
powierzchnia osłonek
zosłonkiB
1
4
i
Ad
i
dd
i
(
)
=
1
4
i
Ad
i
=
0.850 m
=
:=
odległość środka cięzkości osłonek od dolnej
krawędzi belki
e0
zcs zosłonkiB
-
0.104 m
=
:=
Δe
emax e0
-
0.620 m
=
:=
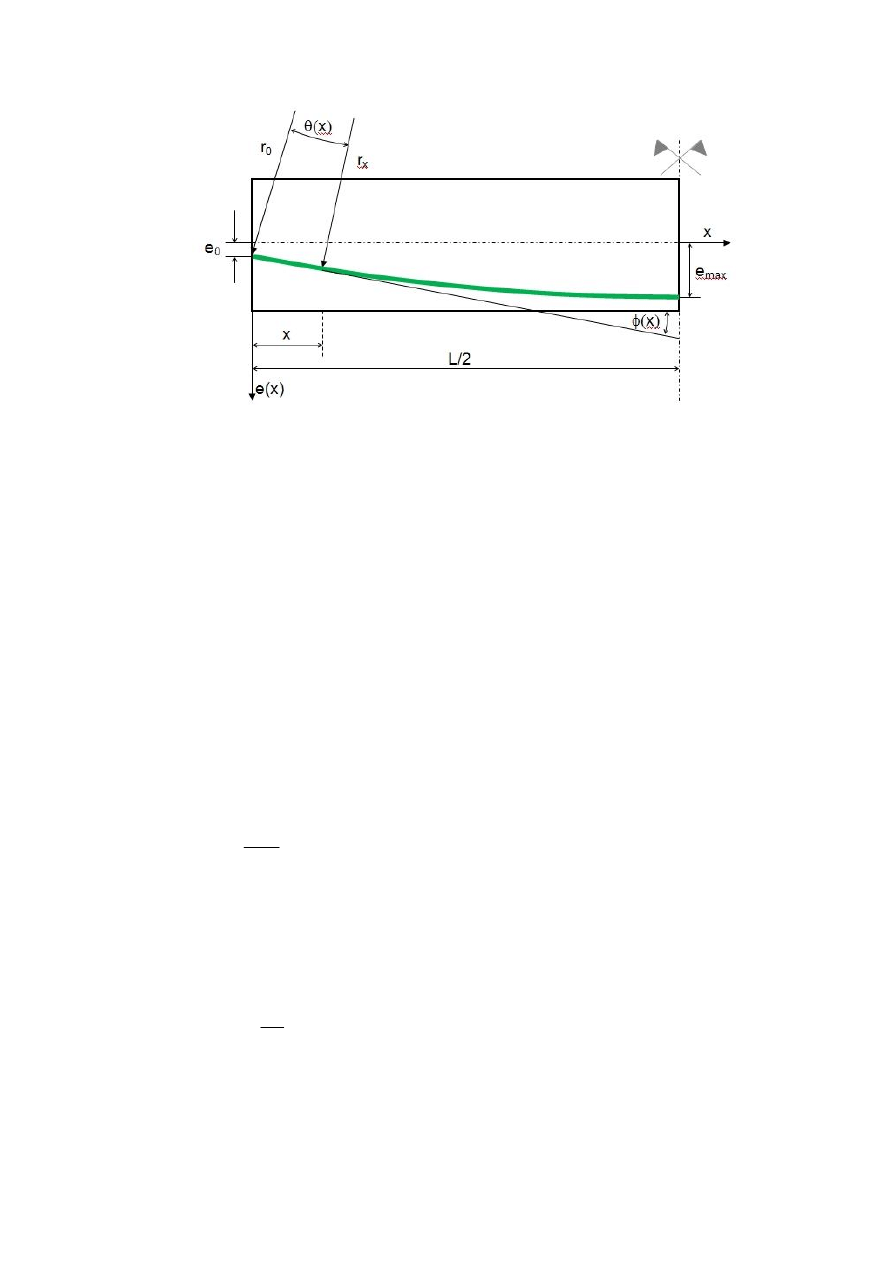
e x
( )
4
Δe
L
2
x
2
4
Δe
L
x
-
e0
+
:=
10.3. Kąt nachylenia trasy kabla wypadkowego do osi podłużnej elementu
ϕ x
( )
4
Δe
L
2
2 x
L
-
(
)
:=
kąt nachylenia w dowolnym punkcie trasy
ϕ 0
( )
5.684
-
deg
=
na czole elementu (x=0)
ϕ
L
2
0.000 deg
=
w połowie rozpiętości elementu (x=L/2)
ϕ L
( )
5.684 deg
=
na końcu elementu (x=4*Δe/L)
10.4. Kąt odgięcia trasy kabla wypadkowego do czoła elementu (zakotwienia czynnego)
θ x
( )
8
Δe
L
2
x
:=
kąt odchylenia w dowolnym punkcie trasy
θ 0
( )
0.000 deg
=
na czole elementu (x=0)
θ
L
2
5.684 deg
=
w połowie rozpiętości elementu (x=L/2)
θ L
( )
11.367 deg
=
na końcu elementu (x=4*Δe/L)
10.5. Średni promień krzywizny trasy kabla
r
L
2
8
Δe
126.008 m
=
:=
17
11. Straty doraźne siły sprężającej
11.1. Przyjęcie siły sprężającej
σpmax
min 0.8 fpk
0.9 fp01k
,
(
)
1488.000 MPa
=
:=
naprężenie maksymalne w stali
sprężającej (str. 70 EC2)
P0max
Approv σpmax
9374.400 kN
=
:=
maksymalna siła naciągu (wzór 5.41 str. 70 EC2)
Przyjęto
P0
9300kN
:=
siła naciągu
11.2. Straty siły sprężającej od tarcia kabli o osłonkę kanału kablowego
lkab
L
25cm
+
25.250 m
=
:=
przyjęta długość kabla
θ x
( )
8
Δe
x
( )
2
x
:=
kąt zakrzywienia trasy cięgna
θ lkab
(
)
0.196
=
μ
0.19
:=
wspołczynnik tarcia między ciegnem a kanałem
kablowym (tab. 5.1 str. 73 EC2)
k
0.005
rad
m
:=
kąt niezamierzony zakrzywienia trasy cięgna
ΔPμ x
( )
P0 1 exp μ
-
θ x
( )
k x
+
(
)
[
]
-
[
]
:=
strata siły spreżającej (wzór 5.45 str. 73 EC2)
ΔPμ lkab
(
)
553.058 kN
=
18

11.3. Straty siły sprężającej od poślizgu cięgna w zakotwieniu
ap
6mm
:=
poślizg kabla w zakotwieniu
x01
ap Ep
Ap
μ k
P0
26.568 m
=
:=
zasięg poślizgu cięgna prostoliniowego
x02
r
μ
ln
1
1
ap μ
Ep
Ap
P0 r
-
21.431 m
=
:=
zasięg poślizgu cięgna krzywoliniowych
x0
max x01 x02
,
(
)
26.568 m
=
:=
zasięg poślizgu cięgna
x0 lkab
1.000
=
warunek spełniony
Krok 1
ap1
lkab
2
μ
k
P0
Ep Ap
5.419 mm
=
:=
ap1 ap
<
1.000
=
warunek spełniony
Krok 2
ap2
ap ap1
-
0.581 mm
=
:=
ΔPsl1 x
( )
max 2ap1
lkab x
-
lkab
2
Ep
Ap
0kN
,
:=
ΔPsl1 0m
(
)
446.168 kN
=
ΔPsl2
ap2
lkab
Ep
Ap
23.904 kN
=
:=
ΔPsl x
( )
ΔPsl1 x
( )
ΔPsl2
+
:=
ΔPsl 0m
(
)
470.071 kN
=
strata siły sprezającej w zakotwieniu od poślizgu
cięgna
11.4. Straty siły sprężającej od odkształceń sprężystych betonu
współczynnik wyrażający stosunek modułu
sprężystości stali sprężająca do modułu sprężystości
betonu belki
αe t0
( )
Ep
Ecm t0
( )
:=
αe 28dni
(
)
5.000
=
19

ρp
Approv
Acs0
0.007
=
:=
współczynnik
n
5
:=
liczba kolejnych naciągów kabli spreżających
ΔPc x t
,
(
)
n
1
-
2n
αe t
( )
ρp
1
zcs0
2
Acs0
Ics0
+
P0 ΔPμ x
( )
-
ΔPsl x
( )
-
(
)
:=
ΔPc
lkab
2
t
0
,
405.248 kN
=
11.5. Siły sprężającej po uwzględnieniu strat doraźnych
Pm0 x t
,
(
)
P0 ΔPμ x
( )
-
ΔPsl x
( )
-
ΔPc x t
,
(
)
-
:=
Pm0
lkab
2
t
0
,
7875.937 kN
=
siła sprężająca po uwzględnienu strat doraźnych
11.6. Sprawdzenie warunku na maksymalne dopuszczalne naprężenie w stali
sprężającej po stratach doraźnych
σPm0.max
min 0.75fpk 0.85fp01k
,
(
)
1.395 GPa
=
:=
maksymalne naprężenie w stali
sprężającej (pkt. 5.10.3. str. 71 EC2)
σPm0
Pm0
lkab
2
t
0
,
Approv
1.250 GPa
=
:=
naprężenie w stali spreżajacej po stratach doraźnych
σPm0 σPm0.max
<
1.000
=
warunek spełniony
12. Straty reologiczne siły sprężającej
12.1. Etapy analizowania strat reologicznych siły sprężającej
Etap "0" - Sprężanie prefabrykowanej belki kablobetonowej
Etap "I" - Montaż belki kablobetonowej w konstrukcji
Etap "II" - Zespolenie belki kablobetonowej z płytami stropowymi dzieki warstwie nadbetonu
Etap "III" - Oddanie obiektu do eksploatacji
Etap "IV" - Analiza pracy konstrukcji w sytuacji trwałej, po 50 latach od oddania obiektu do
eksploatacji
t00
0dni
:=
chwila betonowania belki kablobetonowej
tsp
21dni
:=
chwila spreżenia belki kablobetonowej
20
tmont
30dni
:=
chwila montażu belki kablobetonowej w konstrukcji
tzespol
40dni
:=
chwila zespolenia belki kablobetonowej z nadbetonem
tuzytk
180dni
:=
chwila oddania obiektu do użytkowania
t50
18412dni
:=
chwila analizowania konstrukcji w sytuacji trwałej po
50 latach użytkowania obiektu
tmont.n
tmont tmont
-
0.000 dni
=
:=
chwila montażu dla nadbetonu
tzespol.n
tzespol tmont
-
10.000 dni
=
:=
chwila zespolenia nadbetonu z belką kablobetonową
tuzytk.n
tuzytk tmont
-
150.000 dni
=
:=
chwila oddania obiektu do użytkowania dla nadbetonu
t50.n
t50 tmont
-
1.838
10
4
dni
=
:=
chwila analizowana konstrukcji w sytuacji trwałej po
50 latach użytkowania dla nadbetonu
Zestawienie obciążeń w kolejnych etapach pracy belki kablobetonowej
0
I
II
III
IV
1
a
21,67
-
-
-
-
b
-
22,25
22,25
22,25
22,25
c
-
2,76
-
-
-
d
-
-
2,65
2,65
2,65
e
-
34,20
34,20
34,20
34,20
f
-
-
13,50
13,50
13,50
2
a
-
27,00
27,00
-
-
b
-
-
-
45,00
45,00
Etap
Obciążenie w kN/mb belki
obc. użytkowe
c. własny nadbetonu (świerzy)
c. własny nadbetonu (po
c. własny płyt stropowych
obc. stałe dodatkowe
Obciążenia zmienne [kN/mb]
obc. robocze ludźmi, sprzętem
Obciążenia stałe [kN/mb]
c. własny belki (bez iniekcji)
c. własny belki (iniekcja)
Sytuacja początkowa
AcA0
Acs0 0.928 m
2
=
:=
pole przekroju poprzecznego
zcdA0
zcs0 1.040 m
=
:=
odległość włókien dolnych od środka ciężkości
zcgA0
hb zcs0
-
0.760 m
=
:=
odległość włókien górnych od środka ciężkości
IcA0
Ics0 0.391 m
4
=
:=
moment bezwładności
zcpA0
emax 0.724 m
=
:=
odległość środka ciężkości kabla wypadkowego od
środka ciężkości przekroju
Sytuacja przejściowa
AcAI
Acs 1.124 m
2
=
:=
pole przekroju poprzecznego
zcdAI
zcs
:=
odległość włókien dolnych od środka ciężkości
zcgAI
hb zcs
-
0.846 m
=
:=
odległość włókien górnych od środka ciężkości
21

moment bezwładności
IcAI
Ics 0.516 m
4
=
:=
odległość środka ciężkości kabla wypadkowego od
środka ciężkości przekroju
zcpAI
emax 0.724 m
=
:=
Sytuacja trwała
AcAII
Acs 1.124 m
2
=
:=
pole przekroju poprzecznego
IcAII
Ics 0.516 m
4
=
:=
moment bezwładności
zcpAII
emax 0.724 m
=
:=
odległość środka ciężkości kabla wypadkowego od
środka ciężkości przekroju
12.2. Współczynnik pełzania liniowego betonu belki kablobetonowej
AcA0 0.928 m
2
=
pole przekroju poprzecznego
u
2 hfd hśr
+
hfg
+
(
)
bfd
+
bfg
+
bw
-
5.510 m
=
:=
obwód elementu poddany wysychaniu
h0
2 AcA0
u
336.855 mm
=
:=
miarodajny wymiar elementu [mm]
(zał. B wzór B.6 str.185 EC2)
RH
60
:=
wilgotność względna otoczenia [%]
α1
35
fcm 28dni
(
)
MPa
0.7
0.663
=
:=
współczynnik (zał. B wzór B.8c str 184 EC2)
α2
35
fcm 28 dni
(
)
MPa
0.2
0.889
=
:=
współczynnik (zał. B wzór B.8c str 184 EC2)
α3
35
fcm 28dni
(
)
MPa
0.5
0.745
=
:=
współczynnik (zał. B wzór B.8c str 184 EC2)
ϕRH
1
1
RH
100
-
0.1
3
h0
mm
α1
+
α2
1.228
=
:=
współczynnik zależny od wpływu wilgotności dla
fcm>35MPa (zał. B wzór B3b str. 185 EC2)
βf.cm
16.8
fcm 28dni
(
)
MPa
2.117
=
:=
współczynnik zależny od wytrzymałości średniej
betonu (zał. B wzór B.4 str. 185 EC2)
22
α
0
:=
współczynnik zależny od rodzaju cementu - N
(zał. B str. 186 EC2)
t0
tsp 21.000 dni
=
:=
t0
max t0
9
2
t0
dni
1.2
+
1
+
α
0.5dni
,
21.000 dni
=
:=
wiek betonu w chwili pierwszego
obciążenia z uzględniem rodzaju cementu
(zał. B wzór B.9 str 186 EC2)
β t0
( )
1
0.1
t0
dni
0.20
+
:=
współczynnik zależny od wieku betonu w chwili
obciążenia (zał. B wzór B.5 str. 185 EC2)
βH
1.5 1
0.012 RH
(
)
18
+
h0
mm
250
α3
+
692.988
=
:=
współczynnik zależny od wzglednej
wilgotności i miarodajnego wymiaru
elementu dla fcm>35MPa
(zał. B wzór B.8b str.185 EC2)
βH 1500 α3
1.000
=
warunek spełniony
βc t t0
,
(
)
t
dni
t0
dni
-
βH
t
dni
+
t0
dni
-
0.3
:=
współczynnik zależny od rozwoju pełzania betonu
w czasie (zał. B wzór B.7 str. 185 EC2)
ϕ0 t0
( )
ϕRH βf.cm
β t0
( )
:=
podstawowy współczynnik pełzania
(zał. B wzór B.2 str.185 EC2)
ϕ t t0
,
(
)
ϕ0 t0
( )
βc t t0
,
(
)
:=
współczynnik pełzania (zał. B wzór B.1 str.185 EC2)
Współczyniki pełzania betonu belki kablobetonowej
ϕ t50 tsp
,
(
)
1.326
=
współczynnik pełzania od chwili sprężenia belki do
sytuacji trwałej po 50 latach użytkowania
ϕ t50 tmont
,
(
)
1.239
=
współczynnik pełzania od chwili montażu belki do
wytuacji trwałej po 50 latach użytkowania
ϕ t50 tzespol
,
(
)
1.173
=
współczynnik pełzania od chwili zespolenia belki z
nadbetonem do sytuacji trwałej po 50 latach
użytkowania
ϕ t50 tuzytk
,
(
)
0.879
=
współczynnik pełzania od chwili przekazania do
użytkowania obiektu do sytuacji trwałej po 50 latach
użytkowania
23

Sprawdzenie czy mamy pełzanie liniowe
Mg
gbelki leff
2
8
1822.266 kNm
=
:=
moment zginający od ciężaru własnego belki
w połowie rozpiętości belki kablobetonowej
σcg
Mg
-
zcgA0
IcA0
3.541
-
MPa
=
:=
naprężenia normalne od obciążeń zewnętrznych
rsup
1.05
:=
współczynnik
Pk.sup
rsup Pm0
8269.734 kN
=
:=
górna wartość charakterystyczna siły sprężającej
σcp
Pk.sup
AcA0
Pk.sup zcpA0
zcgA0
IcA0
+
20.544 MPa
=
:=
naprężenia normalne od sprężania
σcx
σcg σcp
+
17.003 MPa
=
:=
całkowite naprężenie normalne
σcx 0.45 fcm t0
( )
<
1.000
=
warunek spełniony
12.3. Współczynnik pełzania liniowego nadbetonu
Acn 0.140 m
2
=
pole przekroju poprzecznego
un
2 hHC265
0.530 m
=
:=
obwód elementu poddany wysychaniu
h0.n
2 Acn
un
530.000 mm
=
:=
miarodajny wymiar elementu [mm]
(zał. B wzór B.6 str.185 EC2)
RH
60
:=
wilgotność względna otoczenia [%]
α1.n
35
fcm.n 28dni
(
)
MPa
0.7
1.169
=
:=
współczynnik (zał. B wzór B.8c str 184 EC2)
α2.n
35
fcm.n 28 dni
(
)
MPa
0.2
1.046
=
:=
współczynnik (zał. B wzór B.8c str 184 EC2)
α3.n
35
fcm.n 28dni
(
)
MPa
0.5
1.118
=
:=
współczynnik (zał. B wzór B.8c str 184 EC2)
24

ϕRH.n
1
1
RH
100
-
0.1
3
h0.n
mm
+
1.494
=
:=
współczynnik zależny od wpływu wilgotności dla
fcm<35MPa (zał. B wzór B3a str. 185 EC2)
βfcm.n
16.8
fcm.n 28dni
(
)
MPa
3.175
=
:=
współczynnik zależny od wytrzymałości średniej
betonu (zał. B wzór B.4 str. 185 EC2)
αn
0
:=
współczynnik zależny od rodzaju cementu - N
(zał. B str. 186 EC2)
t0.n
tzespol.n 10.000 dni
=
:=
t0.n
max t0.n
9
2
t0.n
dni
1.2
+
1
+
αn
0.5dni
,
10.000 dni
=
:=
wiek betonu w chwili pierwszego
obciążenia z uzględniem rodzaju
cementu
(zał. B wzór B.9 str 186 EC2)
β t0.n
(
)
1
0.1
t0.n
dni
0.20
+
:=
współczynnik zależny od wieku betonu w chwili
obciążenia (zał. B wzór B.5 str. 185 EC2)
βH.n
1.5 1
0.012 RH
(
)
18
+
h0.n
mm
250
+
1047.150
=
:=
współczynnik zależny od wzglednej
wilgotności i miarodajnego wymiaru
elementu dla fcm<35MPa
(zał. B wzór B.8b str.185 EC2)
βH.n 1500
1.000
=
warunek spełniony
βc t t0.n
,
(
)
t
dni
t0.n
dni
-
βH
t
dni
+
t0.n
dni
-
0.3
:=
współczynnik zależny od rozwoju pełzania betonu
w czasie (zał. B wzór B.7 str. 185 EC2)
ϕ0 t0.n
(
)
ϕRH βfcm.n
β t0.n
(
)
:=
podstawowy współczynnik pełzania
(zał. B wzór B.2 str.185 EC2)
ϕn t t0.n
,
(
)
ϕ0 t0.n
(
)
βc t t0.n
,
(
)
:=
współczynnik pełzania (zał. B wzór B.1 str.185 EC2)
Współczyniki pełzania nadbetonu
ϕn tuzytk.n t0.n
,
(
)
1.355
=
współczynnik pełzania od chwili pierwszego
obciążenia do przekazania obiektu do użytkowania
ϕn t50.n t0.n
,
(
)
2.288
=
współczynnik pełzania od chwili pierwszego
obciążenia do sytuacji trawłej po 50 latch użytkowania
obiektu
25

12.4. Skurcz betonu belki kablobetonowej
12.4.1. Współczynik skurczu
RH0
100
:=
wilgotność środowiska na poziomie 100%
βRH
1.55 1
RH
RH0
3
-
1.215
=
:=
współczynnik (zał. B wzór B.12 str.186 EC2)
αds1
4
:=
współczynnik dla cementu rodzaju N
αds2
0.12
:=
współczynnik dla cementu rodzaju N
fcm0
10MPa
:=
εcd.0
0.85 220
110
αds1
+
(
)
exp
αds2
-
fcm 28dni
(
)
fcm0
βRH
10
6
-
3.201
10
4
-
=
:=
skurcz przy wysychaniu
(zał. B wzór B.11 str. 186 EC2)
12.4.2. Skurcz spowodowany wysychaniem betonu belki kablobetonowej
czas rozpoczęcia skurczu (dzień zakończenia
pielegnacji)
ts
0dni
:=
βds t ts
,
(
)
t
dni
ts
dni
-
t
dni
ts
dni
-
0.04
h0
mm
3
+
:=
współczynnik opisujący przyrost skrczu do
rozpoczęcia wysychania do rozważanej chwili
(wzór 3.10 str.29 EC2)
kh
0.70
500
h0
mm
-
0.05
200
+
0.741
=
:=
współczynnik zależny od miarodajnego wymiaru
elemetu po interpolacji (tab. 3.3 str.29 EC2)
εcd t ts
,
(
)
βds t ts
,
(
)
kh
εcd.0
:=
odkształcenie skurczowe przy wysychaniu
(wzór 3.9 str. 29 EC2)
Skurcz spowodowany wysychaniem betonu belki kablobetonowej
εcd t t0
,
(
)
βds t ts
,
(
)
βds t0 ts
,
(
)
-
(
)
kh
εcd.0
:=
Skurcz spowodowany wysychaniem betonu belki kablobetonowej pomiędzy
chwilą betonowania i sprężania belki kablobetonowej
εcd tsp ts
,
(
)
βds tsp ts
,
(
)
βds ts ts
,
(
)
-
(
)
kh
εcd.0
:=
εcd tsp ts
,
(
)
1.856
10
5
-
=
26

chwilą sprężania i motażu w konstrukcji belki kablobetonowej
εcd tmont tsp
,
(
)
βds tmont ts
,
(
)
βds tsp ts
,
(
)
-
(
)
kh
εcd.0
:=
εcd tmont tsp
,
(
)
7.094
10
6
-
=
chwilą motażu w konstrukcji belki kablobetonowej i zespoleniem z nadbetonem
εcd tzespol tmont
,
(
)
βds tzespol ts
,
(
)
βds tmont ts
,
(
)
-
(
)
kh
εcd.0
:=
εcd tzespol tmont
,
(
)
7.361
10
6
-
=
chwilą zespolenia belki kablobetonowej z nadbetone i oddania obiektu do użytkowania
εcd tuzytk tzespol
,
(
)
βds tuzytk ts
,
(
)
βds tzespol ts
,
(
)
-
(
)
kh
εcd.0
:=
εcd tuzytk tzespol
,
(
)
6.687
10
5
-
=
chwilą oddania obektu do użytkowania i analizowania konstrukcji w sytuacji trwałej po 50 latach
użytkowania
εcd t50 tuzytk
,
(
)
βds t50 ts
,
(
)
βds tuzytk ts
,
(
)
-
(
)
kh
εcd.0
:=
εcd t50 tuzytk
,
(
)
1.341
10
4
-
=
12.4.3. Skurcz autogeniczny betonu belki klablobetonowej
βas t()
1
exp
0.2
-
t
dni
0.5
-
:=
przyrost skurczu (wzór 3.13 str.29 EC2)
εca.∞
2.5
fck
MPa
10
-
10
6
-
1.125
10
4
-
=
:=
końcowe odkształcenie skurczu autogenicznego
(wzór 3.12 str.29 EC2)
εca t()
βas t() εca.∞
:=
(wzór 3.11 str. 29 EC2)
Skurcz autogeniczny betonu
εca t t0
,
(
)
βas t() βas t0
( )
-
(
)
εca.∞
:=
Skurcz autogeniczny betonu belki kablobetonowej pomiędzy
chwilą betonowania i sprężania belki kablobetonowej
εca tsp ts
,
(
)
βas tsp
( )
βas ts
( )
-
(
)
εca.∞
:=
27

εca tsp ts
,
(
)
6.751
10
5
-
=
chwilą sprężania i motażu w konstrukcji belki kablobetonowej
εca tmont tsp
,
(
)
βas tmont
(
)
βas tsp
( )
-
(
)
εca.∞
:=
εca tmont tsp
,
(
)
7.371
10
6
-
=
chwilą motażu w konstrukcji belki kablobetonowej i zespoleniem z nadbetonem
εca tzespol tmont
,
(
)
βas tzespol
(
)
βas tmont
(
)
-
(
)
εca.∞
:=
εca tzespol tmont
,
(
)
5.864
10
6
-
=
chwilą zespolenia belki kablobetonowej z nadbetone i oddania obiektu do użytkowania
εca tuzytk tzespol
,
(
)
βas tuzytk
(
)
βas tzespol
(
)
-
(
)
εca.∞
:=
εca tuzytk tzespol
,
(
)
2.407
10
5
-
=
chwilą oddania obektu do użytkowania i analizowania konstrukcji w sytuacji trwałej po 50 latach
użytkowania
εca t50 tuzytk
,
(
)
βas t50
( )
βas tuzytk
(
)
-
(
)
εca.∞
:=
εca t50 tuzytk
,
(
)
7.688
10
6
-
=
12.4.4. Całkowite odkształcenie skurczowe betonu belki kablobetnowej
εcs t t0
,
(
)
εcd t t0
,
(
)
εca t t0
,
(
)
+
:=
(wzór 3.8 str. 29 EC2)
Całkowite odkształcenie skurczowe betonu belki kablobetonowej pomiędzy
chwilą betonowania i sprężania belki kablobetonowej
εcs tsp ts
,
(
)
εcd tsp ts
,
(
)
εca tsp ts
,
(
)
+
:=
εcs tsp ts
,
(
)
8.607
10
5
-
=
chwilą sprężania i motażu w konstrukcji belki kablobetonowej
εcs tmont tsp
,
(
)
εcd tmont tsp
,
(
)
εca tmont tsp
,
(
)
+
:=
28

εcs tmont tsp
,
(
)
1.446
10
5
-
=
chwilą motażu w konstrukcji belki kablobetonowej i zespoleniem z nadbetonem
εcs tzespol tmont
,
(
)
εcd tzespol tmont
,
(
)
εca tzespol tmont
,
(
)
+
:=
εcs tzespol tmont
,
(
)
1.322
10
5
-
=
chwilą zespolenia belki kablobetonowej z nadbetone i oddania obiektu do użytkowania
εcs tuzytk tzespol
,
(
)
εcd tuzytk tzespol
,
(
)
εca tuzytk tzespol
,
(
)
+
:=
εcs tuzytk tzespol
,
(
)
9.094
10
5
-
=
chwilą oddania obektu do użytkowania i analizowania konstrukcji w sytuacji trwałej po 50 latach
użytkowania
εcs tuzytk tzespol
,
(
)
εcd tuzytk tzespol
,
(
)
εca tuzytk tzespol
,
(
)
+
:=
εcs t50 tuzytk
,
(
)
1.418
10
4
-
=
12.5. Skurcz nadbetonu
12.5.1. Współczynik skurczu
RH0
100
:=
wilgotność środowiska na poziomie 100%
βRH
1.55 1
RH
RH0
3
-
1.215
=
:=
współczynnik (zał. B wzór B.12 str.186 EC2)
αds1
4
:=
współczynnik dla cementu rodzaju N
αds2
0.12
:=
współczynnik dla cementu rodzaju N
fcm0
10MPa
:=
εcd.n.0
0.85 220
110
αds1
+
(
)
exp
αds2
-
fcm.n 28dni
(
)
fcm0
βRH
10
6
-
4.872
10
4
-
=
:=
skurcz przy wysychaniu
(zał. B wzór B.11 str. 186 EC2)
12.5.2. Skurcz spowodowany wysychaniem nadbetonu
czas rozpoczęcia skurczu (dzień zakończenia
pielegnacji)
ts
0dni
:=
29

βds.n t ts
,
(
)
t
dni
ts
dni
-
t
dni
ts
dni
-
0.04
h0.n
mm
3
+
:=
współczynnik opisujący przyrost skrczu do
rozpoczęcia wysychania do rozważanej chwili
(wzór 3.10 str.29 EC2)
kh
0.70
:=
współczynnik zależny od miarodajnego wymiaru
elemetu (tab. 3.3 str.29 EC2)
εcd.n t ts
,
(
)
βds.n t ts
,
(
)
kh
εcd.n.0
:=
(wzór 3.9 str. 29 EC2)
Skurcz spowodowany wysychaniem nadbetonu
εcd.n t t0
,
(
)
βds.n t ts
,
(
)
βds.n t0 ts
,
(
)
-
(
)
kh
εcd.n.0
:=
Skurcz spowodowany wysychaniem nadbetonu pomiędzy
chwilą motażu w konstrukcji belki kablobetonowej i zespoleniem z nadbetonem
εcd.n tzespol.n tmont.n
,
(
)
βds.n tzespol.n ts
,
(
)
βds.n tmont.n ts
,
(
)
-
(
)
kh
εcd.n.0
:=
εcd.n tzespol.n tmont.n
,
(
)
6.847
10
6
-
=
chwilą zespolenia belki kablobetonowej z nadbetone i oddania obiektu do użytkowania
εcd.n tuzytk.n tespol.n
,
(
)
βds.n tuzytk.n tzespol.n
,
(
)
βds.n tzespol.n ts
,
(
)
-
(
)
kh
εcd.n.0
:=
εcd.n tuzytk.n tzespol.n
,
(
)
6.917
10
5
-
=
chwilą oddania obektu do użytkowania i analizowania konstrukcji w sytuacji trwałej po 50 latach
użytkowania
εcd.n t50.n tuzytk.n
,
(
)
βds.n t50.n tuzytk.n
,
(
)
βds.n tuzytk.n ts
,
(
)
-
(
)
kh
εcd.n.0
:=
εcd.n t50.n tuzytk.n
,
(
)
2.520
10
4
-
=
12.5.3. Skurcz autogeniczny nadbetonu
βas.n t
( )
1
exp
0.2
-
t
dni
0.5
-
:=
przyrost skurczu (wzór 3.13 str.29 EC2)
εca.∞
2.5
fck
MPa
10
-
10
6
-
1.125
10
4
-
=
:=
końcowe odkształcenie skurczu autogenicznego
(wzór 3.12 str.29 EC2)
30

εca.n t()
βas.n t() εca.∞
:=
(wzór 3.11 str. 29 EC2)
Skurcz autogeniczny nadbetonu
εca.n t t0
,
(
)
βas.n t() βas.n t0
( )
-
(
)
εca.∞
:=
Skurcz autogeniczny nadbetonu
chwilą motażu w konstrukcji belki kablobetonowej i zespoleniem z nadbetonem
εca.n tzespol.n tmont.n
,
(
)
βas.n tzespol.n
(
)
βas.n tmont.n
(
)
-
(
)
εca.∞
:=
εca.n tzespol.n tmont.n
,
(
)
5.273
10
5
-
=
chwilą zespolenia belki kablobetonowej z nadbetone i oddania obiektu do użytkowania
εca.n tuzytk.n tzespol.n
,
(
)
βas.n tuzytk.n
(
)
βas.n tzespol.n
(
)
-
(
)
εca.∞
:=
εca.n tuzytk.n tzespol.n
,
(
)
5.006
10
5
-
=
chwilą oddania obektu do użytkowania i analizowania konstrukcji w sytuacji trwałej po 50 latach
użytkowania
εca.n t50.n tuzytk.n
,
(
)
βas.n t50.n
(
)
βas.n tuzytk.n
(
)
-
(
)
εca.∞
:=
εca.n t50.n tuzytk.n
,
(
)
9.713
10
6
-
=
12.5.4. Całkowite odkształcenie skurczowe nadbetonu
εcs.n t t0
,
(
)
εcd.n t t0
,
(
)
εca.n t t0
,
(
)
+
:=
(wzór 3.8 str. 29 EC2)
Całkowite odkształcenie skurczowe nadbetonu
chwilą motażu w konstrukcji belki kablobetonowej i zespoleniem z nadbetonem
εcs.n tzespol.n tmont.n
,
(
)
εcd.n tzespol.n tmont.n
,
(
)
εca.n tzespol.n tmont.n
,
(
)
+
:=
εcs.n tzespol.n tmont.n
,
(
)
5.958
10
5
-
=
chwilą zespolenia belki kablobetonowej z nadbetone i oddania obiektu do użytkowania
εcs.n tuzytk.n tzespol.n
,
(
)
εcd.n tuzytk.n tzespol.n
,
(
)
εca.n tuzytk.n tzespol.n
,
(
)
+
:=
31

εcs.n tuzytk.n tzespol.n
,
(
)
1.192
10
4
-
=
chwilą oddania obektu do użytkowania i analizowania konstrukcji w sytuacji trwałej po 50 latach
użytkowania
εcs.n tuzytk.n tzespol.n
,
(
)
εcd.n tuzytk.n tzespol.n
,
(
)
εca.n tuzytk.n tzespol.n
,
(
)
+
:=
εcs.n t50.n tuzytk.n
,
(
)
2.617
10
4
-
=
12.6. Różnica odkształceń skurczowych nabetonu i belki kablobetonowej
Etap "III" - Oddanie obiektu do eksploatacji
Δt = t
użytk
- t
zespol
aIII
zcgAI 0.5hHC265
+
0.979 m
=
:=
odległość środka ciężkości belki od środka ciężkości
nadbetonu
αcnIII
Ecm.n tuzytk.n
(
)
Ecm 28dni
(
)
0.824
=
:=
współczynnik redukujący
AcnIII
Acn αcnIII
0.116 m
2
=
:=
pole powierzchni nadbetonu zredukowane
adIII
AcnIII
AcAI AcnIII
+
aIII
0.091 m
=
:=
odległość środka ciężkości przekroju zespolonego
od środka ciężkości przekroju belki kablobetonowej
agIII
aIII adIII
-
0.887 m
=
:=
odległość środka ciężkości przekroju zespolonego
od środka ciężkości nadbetonu z uwzględnieniem
pełzania
bn
2 hHC265
0.530 m
=
:=
szerokość nadbetonu
Icn
bn hHC265
3
12
Acn agIII
2
+
:=
moment bezwładności nadbetonu względem środka
ciężkości przekroju zepolonego
ΔεIII
εcs.n tuzytk.n tzespol.n
,
(
)
εcs tuzytk tzespol
,
(
)
-
2.829
10
5
-
=
:=
różnica odkształceń
MskIII
Ecm 28dni
(
) AcAI
ΔεIII
adIII
110.349 kN m
=
:=
momnet wywołany różnicą odkształceń
współczynnikiIII
1
Icn αcnIII
IcAI
+
aIII adIII
AcAI
IcAI
1
1
1.178
0.195
1.000
1.000
=
:=
32

obciążeniaIII
0
MskIII
:=
NbIII
obciążeniaIII
1 0
,
współczynnikiIII
1 0
,
aIII
współczynnikiIII
0 0
,
-
aIII
+
135.075 kN
=
:=
siła podłóżna przyłożona do belki
MbIII
aIII
współczynnikiIII
0 0
,
-
NbIII
112.240
-
kNm
=
:=
moment przyłożony do belki
NnIII
NbIII
-
135.075
-
kN
=
:=
siła podłóżna przyłożona do nadetonu
MnIII
Icn αcnIII
IcAI
MbIII
19.949
-
kNm
=
:=
moment przyłożony do nadbetonu
Napreżenia w nadbetonie
σcngIII
NnIII
Acn
MnIII
Icn
0.5
hHC265
+
0.985
-
MPa
=
:=
naprężenia w włóknach górnych
nadbetonu
σcndIII
NnIII
Acn
MnIII
Icn
0.5
hHC265
-
0.938
-
MPa
=
:=
naprężenia w włóknach dolnych
nadbetonu
Napreżenia w belce
σcgIII
NbIII
AcAI
MbIII
IcAI
zcgAI
+
0.064
-
MPa
=
:=
naprężenia w włóknach górnych belki
σcdIII
NbIII
AcAI
MbIII
IcAI
zcdAI
-
0.328 MPa
=
:=
naprężenia w włóknach dolnych belki
Naprężenia w belce na poziomie kabla wypadkowego
σcs.spIII
NbIII
AcAI
MbIII
IcAI
zcpAI
-
0.278 MPa
=
:=
naprężenia w belce na wysokości kabla
wypadkowego
Etap "IV" - Analiza pracy konstrukcji w sytuacji trwałej, po 50 latach od oddania obiektu do
eksploatacji
Δt = t
50
- t
uzytk
aIV
zcgAI 0.5hHC265
+
0.979 m
=
:=
odległość środka ciężkości belki od środka ciężkości
nadbetonu
33

αcnIV
Ecm.n t50
( )
Ecm t50
( )
0.789
=
:=
współczynnik
AcnIV
Acn αcnIV
0.111 m
2.000
=
:=
pole powierzchni nadbetonu zredukowane
adIV
AcnIV
AcAI AcnIV
+
aIV
0.088 m
=
:=
odległość środka ciężkości przekorju zespolonego od
środka ciężkości przekoroju belki kablobetonowej
agIV
aIV adIV
-
0.891 m
=
:=
odległość środka ciężkości przekorju zespolonego
od środka ciężkości nadbetonu z uwzględnieniem
pełzania
bn
2 hHC265
0.530 m
=
:=
Icn
bn hHC265
3
12
Acn agIV
2
+
:=
moment bezwładności nadbetonu
ΔεIV
εcs.n t50.n tuzytk.n
,
(
)
εcs t50 tuzytk
,
(
)
-
1.199
10
4
-
=
:=
różnica odkształceń
MskIV
Ecm.n 28dni
(
) AcAI
ΔεIV
adIV
355.248 kNm
=
:=
momnet od różnicy odkształceń
współczynnikiIV
1
Icn αcnIV
IcAI
+
aIV adIV
AcAI
IcAI
1
1
1.172
0.187
1.000
1.000
=
:=
obciążeniaIV
0
MskIV
:=
NbIV
obciążeniaIV
1 0
,
współczynnikiIV
1 0
,
aIV
współczynnikiIV
0 0
,
-
aIV
+
432.033 kN
=
:=
siła podłóżna przyłożona do belki
MbIV
aIV
współczynnikiIV
0 0
,
-
NbIV
360.861
-
kNm
=
:=
moment przyłożony do belki
NnIV
NbIV
-
432.033
-
kN
=
:=
siła podłóżna przyłożona do nadetonu
MnIV
Icn αcnIV
IcAI
MbIV
61.940
-
kNm
=
:=
moment przyłożony do nadbetonu
34

Napreżenia w nadbetonie
σcngIV
NnIV
Acn
MnIV
Icn
0.5
hHC265
+
3.149
-
MPa
=
:=
naprężenia w włóknach górnych
nadbetonu
naprężenia w włóknach dolnych
nadbetonu
σcndIV
NnIV
Acn
MnIV
Icn
0.5
hHC265
-
3.003
-
MPa
=
:=
Napreżenia w belce
σcngIV
NbIII
AcAI
MbIII
IcAI
zcgAI
+
0.064
-
MPa
=
:=
naprężenia w włóknach górnych belki
σcndIV
NbIV
AcAI
MbIV
IcAI
zcdAI
-
1.051 MPa
=
:=
naprężenia w włóknach dolnych belki
Naprężenia w belce na poziomie kabla wypadkowego
σcs.spIV
NbIV
AcAI
MbIV
IcAI
zcpAI
-
0.890 MPa
=
:=
naprężenia w belce na wysokości kabla
wypadkowego
Wartości momentów przęsłowych dla kolejnych etapów od prawie stałej kombinacji
obciażeń
Etap "0" - Sprężanie prefabrykowanej belki kablobetonowej
MSd_lt.0
gbelki.1
leff
2
8
1692.969 kNm
=
:=
Etap "I" - Montaż belki kablobetonowej w konstrukcji
ψ2.1_I
0.2
:=
MSd_lt.I
gbelki.2 gnbs
+
gstrop b
+
(
)
ψ2.1_I gr
b
+
leff
2
8
5567.969 kNm
=
:=
Etap "II" - Zespolenie belki kablobetonowej z płytami stropowymi dzieki warstwie nadbetonu
ψ2.1_II
0.2
:=
MSd_lt.II
gbelki.2 gnb
+
gstrop b
+
gdodatkowe b
+
(
)
ψ2.1_II gr
b
+
leff
2
8
6153.906 kNm
=
:=
Etap "III" - Oddanie obiektu do eksploatacji
ψ1.1_III
0.7
:=
ψ2.1_III
0.6
:=
MSd_lt.III
gbelki.2 gnb
+
gstrop b
+
gdodatkowe b
+
(
)
ψ2.1_III q
b
+
leff
2
8
7841.406 kNm
=
:=
35
Etap "IV" - Analiza pracy konstrukcji w sytuacji trwałej, po 50 latach od oddania obiektu do
eksploatacji
ψ1.1_IV
0.7
:=
ψ2.1_IV
0.6
:=
MSd_lt.IV
gbelki.2 gnb
+
gstrop b
+
gdodatkowe b
+
(
)
ψ2.1_IV q
b
+
leff
2
8
7841.406 kNm
=
:=
Przyrosty momentów pomiędzy etapami
ΔMSd_lt.0_I
MSd_lt.I MSd_lt.0
-
3875.000 kNm
=
:=
ΔMSd_lt.I_II
MSd_lt.II MSd_lt.I
-
585.938 kNm
=
:=
ΔMSd_lt.II_III
MSd_lt.III MSd_lt.II
-
1687.500 kNm
=
:=
ΔMSd_lt.III_IV
MSd_lt.IV MSd_lt.III
-
0.000 kNm
=
:=
Naprężenia w betonie od prawie stałej kombinacji obciążeń (na poziomie kabla
wypadkowego)
Przed zespoleniem
Naprężenia w włóknach górnych
σc_g t
( )
Pm0
AcA0
Pm0 zcpA0
zcgA0
IcA0
-
MSd_lt.0 zcgA0
IcA0
+
tsp t
tmont
<
if
Pm0
AcA0
Pm0 zcpAI
zcgAI
IcAI
-
MSd_lt.I zcgAI
IcAI
+
tmont t
tzespol
<
if
:=
Naprężenia w włóknach dolnych
σc_d t
( )
Pm0
AcA0
Pm0 zcpA0
zcdA0
IcA0
+
MSd_lt.0 zcdA0
IcA0
-
tsp t
tmont
<
if
Pm0
AcA0
Pm0 zcpAI
zcdAI
IcAI
+
MSd_lt.I zcdAI
IcAI
-
tmont t
tzespol
<
if
:=
σc t()
Pm0
AcA0
Pm0 zcpA0
zcpA0
IcA0
+
MSd_lt.0 zcpA0
IcA0
-
tsp t
tmont
<
if
Pm0
AcA0
Pm0 zcpAI
zcpAI
IcAI
+
MSd_lt.I zcpAI
IcAI
-
tmont t
tzespol
<
if
:=
36

Δσc_sp
σc tmont
(
)
σc tsp
( )
-
7.228
-
10
6
Pa
=
:=
Po zespoleniu
współczynniki
1
Icn αcnIII
IcAI
+
aIII adIII
AcAI
IcAI
1
1
1.179
0.195
1.000
1.000
=
:=
obciążenia
ΔMSd_lt.I_II
0
:=
Nb_III
obciążenia
0 0
,
współczynniki
0 0
,
aIII
współczynniki
1 0
,
-
aIII
+
118.336
-
kN
=
:=
siła podłóżna przyłożona do belki
Mb_III
aIII
współczynniki
1 0
,
-
Nb_III
595.146 kNm
=
:=
moment przyłożony do belki
Nn_III
Nb_III
-
118.336 kN
=
:=
siła podłóżna przyłożona do nadetonu
moment przyłożony do nadbetonu
Mn_III
Icn αcnIII
IcAI
Mb_III
106.600 kNm
=
:=
Naprężenia w nadbetonie
σcng_III
Nn_III
Acn
Mn_III
Icn
0.5
hHC265
+
0.968 MPa
=
:=
naprężenia w włóknach górnych
nadbetonu
σcnd_III
Nn_III
Acn
Mn_III
Icn
0.5
hHC265
-
0.717 MPa
=
:=
naprężenia w włóknach dolnych
nadbetonu
Napreżenia w betonie belki
σcg_III
Nb_III
AcAI
Mb_III
IcAI
zcgAI
+
0.870 MPa
=
:=
naprężenia w włóknach górnych belki
σcd_III
Nb_III
AcAI
Mb_III
IcAI
zcdAI
-
1.205
-
MPa
=
:=
naprężenia w włóknach dolnych belki
37
Naprężenia w belce na poziomie kabla wypadkowego
naprężenia w belce na wysokości kabla
wypadkowego
σcd.sp_III
Nb_III
AcAI
Mb_III
IcAI
zcpAI
-
0.940
-
MPa
=
:=
współczynniki
1
Icn αcnIV
IcAI
+
aIV adIV
AcAI
IcAI
1
1
1.172
0.187
1.000
1.000
=
:=
obciążenia
ΔMSd_lt.II_III
0
:=
Nb_IV
obciążenia
0 0
,
współczynniki
0 0
,
aIV
współczynniki
1 0
,
-
aIV
+
327.901
-
kN
=
:=
siła podłóżna przyłożona do belki
Mb_IV
aIV
współczynniki
1 0
,
-
Nb_IV
1714.165 kNm
=
:=
moment przyłożony do belki
Nn_IV
Nb_IV
-
327.901 kN
=
:=
siła podłóżna przyłożona do nadetonu
moment przyłożony do nadbetonu
Mn_IV
Icn αcnIV
IcAI
Mb_IV
294.229 kNm
=
:=
Naprężenia w nadbetonie
naprężenia w włóknach górnych
nadbetonu
σcng_IV
Nn_IV
Acn
Mn_IV
Icn
0.5
hHC265
+
2.682 MPa
=
:=
naprężenia w włóknach dolnych
nadbetonu
σcnd_IV
Nn_IV
Acn
Mn_IV
Icn
0.5
hHC265
-
1.987 MPa
=
:=
Naprężenia w betonie belki
σcg_IV
Nb_III
AcAI
Mb_III
IcAI
zcgAI
+
0.870 MPa
=
:=
naprężenia w włóknach górnych belki
38

σcd_IV
Nb_IV
AcAI
Mb_IV
IcAI
zcgAI
-
3.101
-
MPa
=
:=
naprężenia w włóknach dolnych belki
Naprężenia w belce na poziomie kabla wypadkowego
naprężenia w belce na wysokości kabla
wypadkowego
σcd.sp_IV
Nb_IV
AcAI
Mb_IV
IcAI
zcpAI
-
2.695
-
MPa
=
:=
12.7. Relaksacja stali spreżającej
Naprężenia w kablu wypadkowym od siły Pm0 i długotrwałej kombinacji obciążeń
(z uwzględnienim naprężeń skurczowych)
σpi.sp
Pm0
Approv
1250.149 MPa
=
:=
współczynnik wyrażający stosunek modułu
sprężystości stali sprężającej do modułu
sprężystości betonu belki w czasie montarzu
αp tmont
(
)
Ep
Ecm tmont
(
)
:=
σpi.mont
Pm0
Approv
MSd_lt.I zcpA0
IcA0
αp tmont
(
)
+
:=
σpi.mont 1301.516 MPa
=
współczynnik wyrażający stosunek modułu
sprężystości stali sprężającej do modułu
sprężystości betonu belki w czasie zespolenia
αp tzespol
(
)
Ep
Ecm tzespol
(
)
:=
σpi.zespol
Pm0
Approv
MSd_lt.I zcpA0
IcA0
αp tzespol
(
)
+
σcd.sp_III σcs.spIII
-
(
)
αp tzespol
(
)
-
:=
σpi.zespol 1307.032 MPa
=
współczynnik wyrażający stosunek modułu
sprężystości stali sprężającej do modułu
sprężystości betonu belki w czasie zespolenia
αp tuzytk
(
)
Ep
Ecm tzespol
(
)
:=
σpi.uzytk
Pm0
Approv
MSd_lt.I zcpA0
IcA0
αp tuzytk
(
)
+
σcd.sp_IV σcs.spIV
-
(
)
αp tuzytk
(
)
-
σcd.sp_III σcs.spIII
+
(
)
αp tuzytk
(
)
+
...
:=
σpi.uzytk 1315.458 MPa
=
σpi.50
σpi.uzytk 1315.458 MPa
=
:=
39
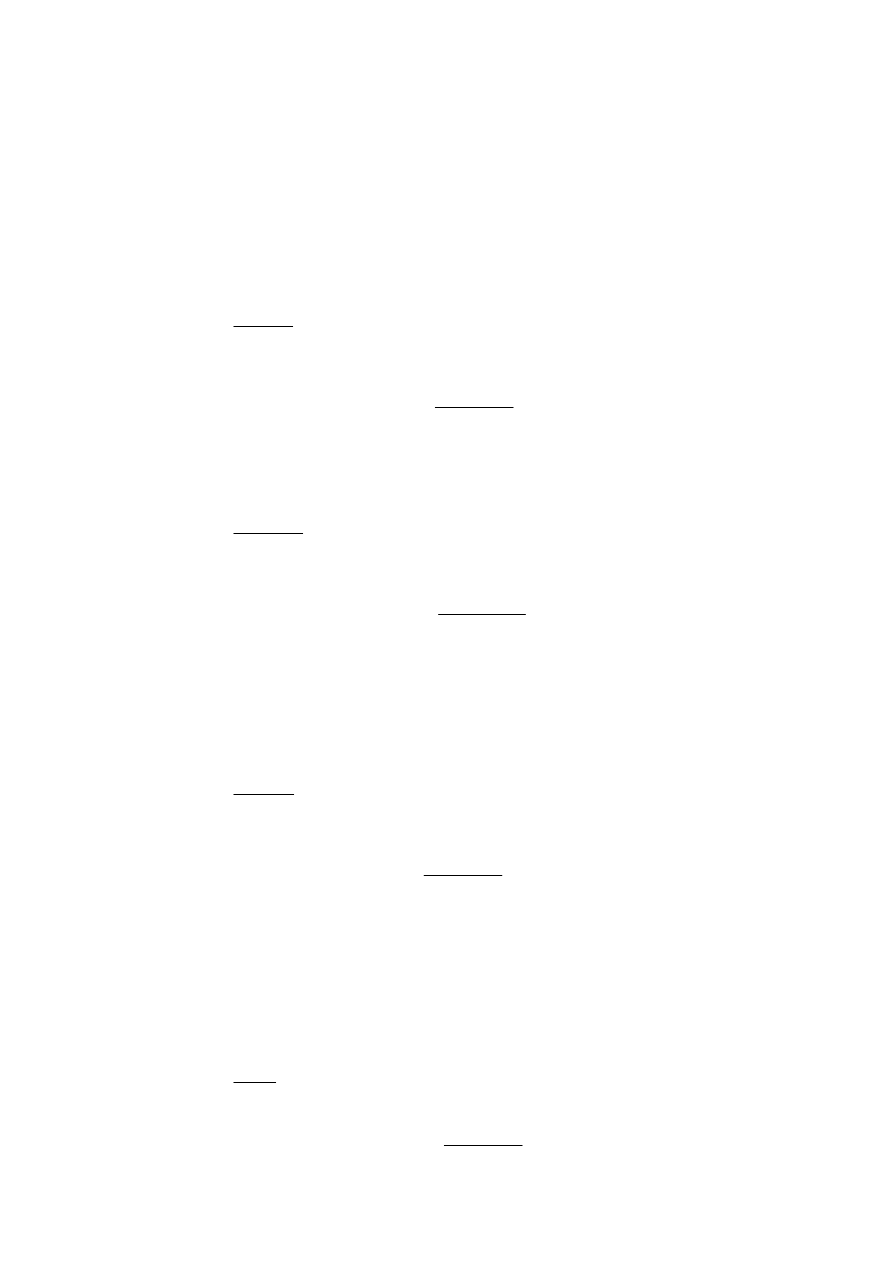
Straty od częściowej relaksacji stali sprężającej pomiędzy
ρ1000
2.5
:=
wartość strat od relaksacji po 1000 godzinach
obciążenia przy średniaj temp. 20 stopni C dla klasy
stali 2 w [%]
(pkt. 3.3.2(6) str. 38 EC2)
chwilą sprężania i motażu w konstrukcji belki kablobetonowej
μ1
σpi.mont
fpk
0.700
=
:=
współczynnik wytężenia stali sprężającej
Δσpr.I
0.66
ρ1000
exp 9.09
μ1
(
)
tmont tsp
-
1000 hr
0.75 1
μ1
-
(
)
10
5
-
σpi.sp
8.452 MPa
=
:=
chwilą motażu w konstrukcji belki kablobetonowej i zespoleniem z nadbetonem
μ2
σpi.zespol
fpk
0.703
=
:=
współczynnik wytężenia stali sprężającej
Δσpr.II
0.66
ρ1000
exp 9.09
μ2
(
)
tzespol tsp
-
1000hr
0.75 1
μ2
-
(
)
10
5
-
σpi.mont Δσpr.I
+
(
)
Δσpr.I
-
:=
Δσpr.II 2.333 MPa
=
chwilą zespolenia belki kablobetonowej z nadbetone i oddania obiektu do użytkowania
μ3
σpi.uzytk
fpk
0.707
=
:=
współczynnik wytężenia stali sprężającej
Δσpr.III
0.66
ρ1000
exp 9.09
μ3
(
)
tuzytk tsp
-
1000 hr
0.75 1
μ3
-
(
)
10
5
-
σpi.uzytk Δσpr.I
+
Δσpr.II
+
(
)
1
-
(
)
Δσpr.I Δσpr.II
-
(
)
+
...
:=
Δσpr.III 12.069 MPa
=
chwilą oddania obektu do użytkowania i analizowania konstrukcji w sytuacji trwałej po 50 latach
użytkowania
μ4
σpi.50
fpk
0.707
=
:=
współczynnik wytężenia stali sprężającej
Δσpr.IV
0.66
ρ1000
exp 9.09
μ4
(
)
tuzytk tsp
-
1000hr
0.75 1
μ4
-
(
)
10
5
-
σpi.uzytk Δσpr.I
+
Δσpr.II
+
(
:=
40
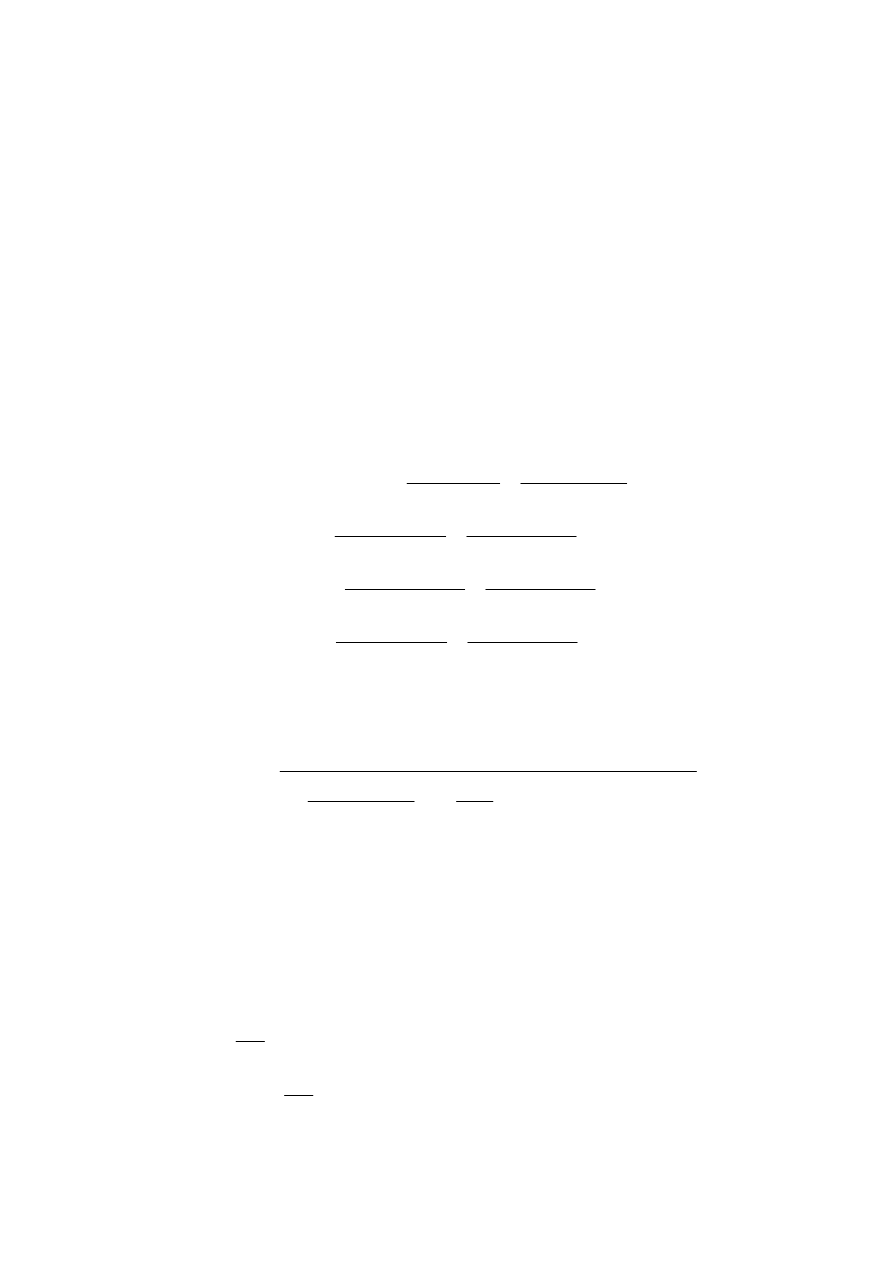
Całkowita warotść strat spowodowanych relaksacja stali
Δσpr
Δσpr.I Δσpr.II
+
Δσpr.III
+
Δσpr.IV
+
18.354 MPa
=
:=
12.8. Straty reologiczne siły sprężającej
σc tsp
( )
15.901 MPa
=
Δσc.mont
Δσc_sp
7.228
-
MPa
=
:=
Δσc.zespol
σcd.sp_III σcs.spIII
+
0.662
-
MPa
=
:=
Δσc.uzytk
σcd.sp_IV σcs.spIV
+
1.805
-
MPa
=
:=
εtot
εcs t50 tsp
,
(
)
σc tsp
( )
1
1.05 Ecm tsp
( )
ϕ t50 tsp
,
(
)
1.05 Ecm 28dni
(
)
+
+
Δσc.mont
1
1.05 Ecm tmont
(
)
ϕ t50 tmont
,
(
)
1.05 Ecm 28dni
(
)
+
+
...
Δσc.zespol
1
1.05 Ecm tzespol
(
)
ϕ t50 tzespol
,
(
)
1.05 Ecm 28dni
(
)
+
+
...
Δσc.uzytk
1
1.05 Ecm tuzytk
(
)
ϕ t50 tuzytk
,
(
)
1.05 Ecm 28dni
(
)
+
+
...
:=
εtot 6.680 10
4
-
=
Δσp.c.s.r
εtot Ep
0.8
Δσpr
+
1
Ep Approv
Ecm t50
( )
AcAII
1
AcAII
IcAII
zcpAII
2
+
1
0.8
ϕ t50 tsp
,
(
)
+
(
)
+
127.001 MPa
=
:=
ΔPc.s.r
Ap Δσp.c.s.r
694.769 kN
=
:=
12.9. Obliczenie siły naciągu kabla wypadkowego po uwzględnieniu strat
doraźnych i reologicznych
Pm0
lkab
2
t
0
,
7875.937 kN
=
siła sprężająca po uwzględnieniu strata doraźnych
Pmt
Pm0
lkab
2
t
0
,
ΔPc.s.r
-
7181.168 kN
=
:=
siła sprężająca po stratach reologicznych
P0 9300.000 kN
=
przyjęta siła naciągu
41

P0 Pmt
-
P0
22.783 %
=
ilość strat naciągu w kablu wypadkowym
σpmt
Pmt
Approv
1139.868 MPa
=
:=
naprężenia w kablu wypadkowym
0.65 fpk
1209.000 MPa
=
σpmt 0.65 fpk
1.000
=
warunek spełniony
13. Sytuacja początkowa w konstrukcji sprężonej
13.1. Ograniczenie naprężeń w betonie (str. 108 EC2)
fck t
( )
fcm t
( )
8MPa
-
(
)
t
28dni
<
if
fck otherwise
:=
charakterystyczna wytrzymałość na ściskanie betonu
w czasie
y
zcgA0
-
zcdA0
0.760
-
1.040
m
=
:=
odległość środka cięzokości od skrajnuch włókien
σcN_I
MSd_lt.0
-
y
IcA0
3.290
4.497
-
MPa
=
:=
naprężenia normalne od obciążeń zewnętrznych
σcp_I
Pk.sup
AcA0
Pk.sup zcpA0
y
IcA0
+
2.722
-
24.813
MPa
=
:=
naprężenia normalne od sprężenia
σcx_I
σcN_I σcp_I
+
0.568
20.316
Pa
=
:=
całkowite naprężenia normalne od sprężania
0.6 fck t0
( )
31.566 MPa
=
wartośc naprężeń ściskających ograniczjąca
σcx_I 0.6 fck t0
( )
1.000
1.000
=
warunek spełniony
fctm t
0
( )
4.041 MPa
=
wartośc naprężeń rozciągających ograniczjąca
σcx_I
fctm t0
( )
-
1.000
1.000
=
warunek spełniony
42

13.2. Stan graniczny ugięć
IcA0 3.913 10
7
cm
4
=
moment bezwładności elementu niezarysowanego
Ecm t0
( )
3.756
10
4
MPa
=
moduł sprężystości betonu
B t0
( )
IcA0 Ecm t0
( )
:=
B t0
( )
1.470
10
4
MN m
2
=
sztywność elementu
MSd_lt.0 1692.969 kNm
=
moment charakterystyczny od ciężaru własnego
αk_I
5
48
:=
współczynnik dla ugiecia od ciężaru własnego
ak_I
αk_I
MSd_lt.0
B t0
( )
leff
2
7.499 mm
=
:=
ugiecie od ciężaru własnego
ap_I
Pk.sup
-
leff
2
48 B t0
( )
5 emax
e0
+
(
)
27.275
-
mm
=
:=
ugiecie od sprężania
aI
ak_I ap_I
+
19.777
-
mm
=
:=
całkowite ugięcie w sytuacji początkowej
alim_I
leff
250
100.000 mm
=
:=
dopuszczalne ugięcie (str. 116 EC2)
aI
alim_I
1.000
=
warunek spełniony
14. Sytuacja trwała w konstrukcji sprężonej
14.1. Ograniczenie naprężeń w betonie (str. 108 EC2)
γinf
0.95
:=
współczynnik bezpieczeństwa (pkt.5.10.9 str. 75 EC2)
γsup
1.05
:=
współczynnik bezpieczeństwa (pkt.5.10.9 str. 75 EC2)
Pk.inf
γinf Pmt
6822.109 kN
=
:=
dolna wartość siły sprężającej
Pk.sup
γsup Pmt
7540.226 kN
=
:=
górna wartość siły sprężającej
Konwenkcja zankowania
"+" - ściskanie lub rozciąganie włókien dolnych
" -" - rozciąganie lub rozciąganie włókien górnych
43
Etap 0 - I
MSd_lt.0 1692.969 kNm
=
moment zginający belke
ΔMSd_lt.0_I 3875.000 kNm
=
różnica momentu zginającego belke
Naprężenia w włóknach górnych
σcg.0_I
Pk.sup
AcAI
Pk.sup zcpAI
zcgAI
IcAI
-
MSd_lt.0 ΔMSd_lt.0_I
+
(
)
zcgAI
IcAI
+
6.890 MPa
=
:=
Naprężenia w włóknach dolnych
σcd.0_I
Pk.inf
AcAI
Pk.inf zcpAI
zcdAI
IcAI
+
MSd_lt.0 ΔMSd_lt.0_I
+
(
)
zcdAI
IcAI
-
4.908 MPa
=
:=
Etap I - II
ΔMSd_lt.I_II 585.938 kNm
=
różnica momentu zginającego belke
Naprężenia w włóknach górnych
σcg.I_II
Pk.sup
AcAI
Pk.sup zcpAI
zcgAI
IcAI
-
ΔMSd_lt.I_II zcgAI
IcAI
+
1.274
-
MPa
=
:=
Naprężenia w włóknach dolnych
σcd.I_II
Pk.inf
AcAI
Pk.inf zcpAI
zcdAI
IcAI
+
ΔMSd_lt.I_II zcdAI
IcAI
-
14.112 MPa
=
:=
Etap II - III
αcnII
Ecm.n tzespol.n
(
)
Ecm 28dni
(
)
0.751
=
:=
współczynnik redukujący
aII
zcgAI 0.5hHC265
+
0.979 m
=
:=
odległość środka ciężkości belki od środka ciężkości
nadbetonu
AcnII
Acn αcnII
0.105 m
2
=
:=
pole powierzchni nadbetonu zredukowane
adII
AcnII
AcAI AcnII
+
aII
0.084 m
=
:=
odległość środka ciężkości przekroju zespolonego
od środka ciężkości przekroju belki kablobetonowej
44
agII
aII adII
-
0.895 m
=
:=
odległość środka ciężkości przekroju zespolonego
od środka ciężkości nadbetonu z uwzględnieniem
pełzania
ΔMSd_lt.II_III 1687.500 kNm
=
moment zginający belke
współczynniki
1
Icn αcnII
IcAI
+
aII adII
AcAI
IcAI
1
1
1.163
0.179
1.000
1.000
=
:=
obciążenia
ΔMSd_lt.II_III
0
:=
Nb_II
obciążenia
0 0
,
współczynniki
0 0
,
aII
współczynniki
1 0
,
-
aII
+
313.146
-
kN
=
:=
siła podłóżna przyłożona do belki
w środku ciężkości
Mb_II
aII
współczynniki
1 0
,
-
Nb_II
1714.208 kNm
=
:=
moment przyłożony do belki
podstawowej
Nn_II
Nb_II
-
313.146 kN
=
:=
siła podłóżna przyłożona do nadetonu
w środku ciężkości
Mn_II
Icn αcnII
IcAI
Mb_II
279.747 kNm
=
:=
moment przyłożony do nadbetonu
Naprężenia w nadbetonie
naprężenia w włóknach górnych
nadbetonu
Δσcng.II_III
Nn_II
Acn
Mn_II
Icn
0.5
hHC265
+
2.560 MPa
=
:=
naprężenia w włóknach dolnych
nadbetonu
Δσcnd.II_III
Nn_II
Acn
Mn_II
Icn
0.5
hHC265
-
1.899 MPa
=
:=
Naprężenia w betonie belki
Δσcg.II_III
Nb_II
AcAI
Mb_II
IcAI
zcgAI
+
2.531 MPa
=
:=
naprężenia w włóknach górnych belki
Δσcd.II_III
Nb_II
AcAI
Mb_II
IcAI
zcgAI
-
3.088
-
MPa
=
:=
naprężenia w włóknach dolnych belki
45
Etap III - IV
ΔMSd_lt.III_IV 0.000 kNm
=
róznica momentu zginającego belke
współczynniki
1
Icn αcnIII
IcAI
+
aIII adIII
AcAI
IcAI
1
1
1.179
0.195
1.000
1.000
=
:=
obciążenia
ΔMSd_lt.III_IV
0
:=
Nb_III
obciążenia
0 0
,
współczynniki
0 0
,
aIII
współczynniki
1 0
,
-
aIII
+
0.000 kN
=
:=
siła podłóżna przyłożona do belki
w środku ciężkości
Mb_III
aIII
współczynniki
1 0
,
-
Nb_III
0.000 kNm
=
:=
moment przyłożony do belki
podstawowej
Nn_III
Nb_III
-
0.000 kN
=
:=
siła podłóżna przyłożona do nadetonu
w środku ciężkości
Mn_III
Icn αcnIII
IcAI
Mb_III
0.000 kNm
=
:=
moment przyłożony do nadbetonu
Naprężenia w nadbetonie
naprężenia w włóknach górnych
nadbetonu
Δσcng.III_IV
Nn_III
Acn
Mn_III
Icn
0.5
hHC265
+
0.000 MPa
=
:=
naprężenia w włóknach dolnych
nadbetonu
Δσcnd.III_IV
Nn_III
Acn
Mn_III
Icn
0.5
hHC265
-
0.000 MPa
=
:=
Naprężenia w betonie belki
Δσcg.III_IV
Nb_III
AcAI
Mb_III
IcAI
zcgAI
+
0.000 MPa
=
:=
naprężenia w włóknach górnych belki
Δσcd.III_IV
Nb_III
AcAI
Mb_III
IcAI
zcgAI
-
0.000 MPa
=
:=
naprężenia w włóknach dolnych belki
46
Całkowite naprężenie w betonie na krawędziach przekroju od charakterystycznej
kombinacji obciążeń
Naprężenia w włóknach górnych
σcx.g
σcg.0_I σcg.I_II
+
Δσcg.II_III
+
Δσcg.III_IV
+
8.146 MPa
=
:=
Naprężenia w włóknach dolnych
σcx.d
σcd.0_I σcd.I_II
+
Δσcd.II_III
+
Δσcd.III_IV
+
15.931 MPa
=
:=
0.6 fck 28dni
(
)
33.000 MPa
=
wartość naprężeń ściskających ograniczjąca
σcx.g 0.6 fck 28dni
(
)
1.000
=
warunek spełniony
fctm 28dni
(
)
4.200 MPa
=
wartość naprężeń rozciągających ograniczjąca
σcx.d
fctm 28dni
(
)
-
1.000
=
warunek spełniony
14.2. Rysy prostopadłe
Wc_I
IcAI
zcdAI
5.413
10
5
cm
3
=
:=
wskaźnik wytrzymałości przekroju
σcp_II
Pk.inf
AcAI
Pk.inf zcpAI
zcdAI
IcAI
+
15.194 MPa
=
:=
naprężenia od sprężania belki
Mcr
Wc_I σcp_II fctm 28dni
(
)
+
(
)
1.050
10
4
kNm
=
:=
moment rysujący
MSd_lt.III_IV
ΔMSd_lt.0_I ΔMSd_lt.I_II
+
ΔMSd_lt.II_III
+
ΔMSd_lt.III_IV
+
6148.438 kNm
=
:=
MSd_lt.III_IV Mcr
1.000
=
warunek spełniony
Sprawdzenie warunku dekompresji - kombinacja prawie stała
ydec
zcdAI dd
1
-
25mm
+
0.779 m
=
:=
odległość rozpatrywanego włókna od środka
Wdec
IcAI
ydec
6.629
10
5
cm
3
=
:=
wskaźnik rozpatrywango włókna
σcp.dec
Pk.inf
AcAI
Pk.inf zcpAI
ydec
IcAI
+
13.520 MPa
=
:=
naprężenie od sprężania
Mdec
Wdec σcp.dec
8962.788 kNm
=
:=
moment dekopresji
47

MSd_lt.IV Mdec
1.000
=
warunek spełniony
14.3. Rysy ukośne
dp
hb ap
-
1.794 m
=
:=
wysokość użyteczna przekroju
VSd_ch
leff
2
dp
-
gbelki.2 gnb
+
gstrop b
+
gdodatkowe b
+
(
)
q b
+
1267.269 kN
=
:=
wartość siły poprzecznej od
kombinacji charakterystycznej
w odległości d.p od podpory
MSd_chIII_IV
gbelki.2 gnb
+
gstrop b
+
gdodatkowe b
+
(
)
q b
+
leff
dp
2
1
dp
leff
-
2463.964 kNm
=
:=
wartość momentu od
kombinacji charakterystycznej
w odległości d.p od podpory
w
zcgAI hfg
-
(
)
-
0
zcdAI hfd
-
0.546
-
0.000
0.654
m
=
:=
odległość rozpatrywanych włókien
j
0
2
..
:=
σx
j
MSd_chIII_IV
-
w
j
IcAI
Pk.inf
AcAI
+
Pk.inf zcpAI
w
j
IcAI
+
:=
σx
3.454
6.071
9.204
MPa
=
naprężenia podłużne od sprężania
i obciążen zewnętrznych
Sc
bfg hfg
zcgAI
hfg
2
-
bfg bw
-
(
)
hfg
zcgAI
hfg
2
-
bw
zcgAI
2
2
+
bfd hfd
zcdAI
hfd
2
-
:=
Sc
2.715
10
5
3.073
10
5
2.050
10
5
cm
3
=
moment statyczny figur nad
rozpatrywanymi włóknami względem
środka ciężkości przekroju
τxy
j
Sc
j
VSd_ch
bw IcAI
:=
τxy
2.776
10
6
3.142
10
6
2.096
10
6
Pa
=
naprężenia ścinające
48

σy
0MPa
:=
naprężenia prostopadłe do osi belki
σc
j
σx
j
σy
+
2
σx
j
σy
-
2
2
τxy
j
2
+
+
:=
główne naprężenia rozciągające
σc
j
σx
j
σy
+
2
σx
j
σy
-
2
2
τxy
j
2
+
-
:=
główne naprężenia rozciągające
Tσ
j
σx
j
τxy
j
τxy
j
σy
:=
macierz naprężeń
eigenvals Tσ
0
4.997
1.543
-
MPa
=
wartości własne naprężeń dla włókien górnych
eigenvals Tσ
1
7.405
1.334
-
MPa
=
wartości własne naprężeń dla włókien środkowych
eigenvals Tσ
2
9.659
0.455
-
MPa
=
wartości własne naprężeń dla włókien dolnych
min eigenvals Tσ
0
eigenvals Tσ
1
,
eigenvals Tσ
2
,
1.543
-
10
6
Pa
=
min eigenvals Tσ
0
eigenvals Tσ
1
,
eigenvals Tσ
2
,
fctm 28dni
(
)
1.000
=
warunek spełniony
14.4. Stan graniczy ugięć
IcA0 3.913 10
7
cm
4
=
moment bezwładności przekorju w stytuacji
początkowej
IcAI 5.163 10
7
cm
4
=
moment bezwładności przekorju w stytuacji
przejściowej
IcAII 5.163 10
7
cm
4
=
moment bezwładności przekorju w stytuacji trwałej
Ecm t0
( )
3.756
10
4
MPa
=
moduł sprężystości dla chwili sprężania belki
Ecm 28dni
(
)
3.800
10
4
MPa
=
moduł sprężystości dla chwili 28 dni
B0
IcA0 Ecm t0
( )
1.470
10
4
MN m
2
=
:=
sztywność belki
49
BI
IcAI Ecm 28dni
(
)
1.962
10
4
MN m
2
=
:=
sztywność belki
BII
IcAII Ecm 28dni
(
)
1.962
10
4
MN m
2
=
:=
sztywność belki
MSd_lt.0 1692.969 kNm
=
moment - Etap 0
ΔMSd_lt.0_I 3875.000 kNm
=
różnica momentów - Etap 0 i Etap I
MSd_lt.I
MSd_lt.0 ΔMSd_lt.0_I
+
5567.969 kNm
=
:=
moment - Etap I
ΔMSd_lt.I_II 585.938 kNm
=
różnica momentów - Etap I i Etap II
ΔMSd_lt.II_III 1687.500 kNm
=
różnica momentów - Etap II i Etap III
ΔMSd_lt.III_IV 0.000 kNm
=
różnica momentów - Etap III i Etap IV
a
Pk.inf
-
5 emax
e0
+
(
)
5 MSd_lt.I
+
48B0
1
ϕ t50 tsp
,
(
)
+
(
)
5
ΔMSd_lt.I_II
48BI
1
ϕ t50 tmont
,
(
)
+
(
)
+
...
5
ΔMSd_lt.II_III
48BII
1
ϕ t50 tzespol
,
(
)
+
(
)
+
...
5
ΔMSd_lt.III_IV
48BII
1
ϕ t50 tuzytk
,
(
)
+
(
)
+
...
leff
2
21.547 mm
=
:=
ugięcie belki
alim
leff
250
100.000 mm
=
:=
dopuszczalne ugięcie belki (str. 116 EC2)
a
alim
1.000
=
warunek spełniony
14.4. Stan graniczy nosności - zginanie (metoda uproszczona)
Mid Md Mnd
+
=
nosność belki zespolonej
Md
- nośność belki podstawowej
Mnd - nośność nadbetonu
Z warunku równowagi sił Acn*f.cnd = A.pn*f.pd otrzymujemy:
Apn
fcd.n
fpd
Acn
0.001 m
2
=
:=
powierzchnia zbrojenia spreżajacego przypisana
nośności nadbetonu
hi
hb hHC265
+
2.065 m
=
:=
wysokość belki zespolonej
50
apA
zosłonkiA 0.230 m
=
:=
odległość środka ciężkości kabli sprężajacych od
dolnej krawędzi w przęśle
x0n
hHC265
2
0.133 m
=
:=
odległość środka ciężkości nadbetonu od górnej
krawędzi
Mnd
Apn fpd
hi ap
-
x0n
-
(
)
3607.692 kNm
=
:=
nośność nadbetonu
Reszta zbrojenia sprężającego odpowiada za nośnoć belki podstawowej
Ap Api Apn
-
=
Api
Approv 63.000 cm
2
=
:=
powierzchnia przyjętogo zbrojenia sprężajacego
Acc.eff
fpd
fcd
Ap Apn
-
(
)
0.166 m
2
=
:=
pole powierzchni efektywne strefy ściskanej
h
hb 1.800 m
=
:=
wysokość belki podstawowej
xeff
Acc.eff
bfg
0.128 m
=
:=
wysokość strefy ściskanej
xeff hfg
1.000
=
warunek spełniony - przekrój pozornie teowy
x0
xeff
2
0.064 m
=
:=
połowa wysokości strefy ściskanej
Md
Api Apn
-
(
)
fpd
h
ap
-
x0
-
(
)
1.263
10
4
kNm
=
:=
nośność belki podstawowej
Mid
Mnd Md
+
1.623
10
4
kNm
=
:=
nośność przekroju zespolonego
MRd_zespol
Mid 1.623 10
4
kNm
=
:=
nośność przekroju zespolonego
MSd
MSd_lt.IV 7841.406 kNm
=
:=
moment zginający belkę zespoloną
MSd
MRd_zespol
0.483
=
MSd
MRd_zespol
1
1.000
=
warunek spełniony
14.5. Stan graniczy nosności - ścinanie
VEd x
( )
leff
2
x
-
ξ γGjsup
gbelki gstrop b
+
gdodatkowe b
+
(
)
γQ1 q
b
+
:=
51

VEd dp
( )
1595.207 kN
=
maksymalna obliczeniowa siła tnąca w odległości d.p
od podpory
NEd
Pmt 7181.168 kN
=
:=
maksymalna obliczeniowa siła podłużna
ϕ x
( )
4
Δe
leff
2
2 x
leff
-
(
)
:=
ϕ dp
( )
0.085
-
rad
=
VEd.red x
( )
VEd x
( )
Pmt sin ϕ x
( )
(
)
-
:=
VEd.red dp
( )
985.808 kN
=
siła tnąca zredukowana
bw.red
bw 0.5 ϕosłonki
-
0.210 m
=
:=
zredukowana szerokość środnika
hb 1.800 m
=
wysokość belki
apA
zosłonkiA 0.230 m
=
:=
odległość środka ciężkości kabli sprężajacych od
dolnej krawędzi w przęśle
dp
hb apA
-
1.570 m
=
:=
wysokość użyteczna przekroju podciągu
AsBprov
32
π 16mm
(
)
2
4
64.340 cm
2
=
:=
AsL
AsBprov 64.340 cm
2
=
:=
pole przekroju zbrojenia nad podporą
Wymiarowanie podciągu ze względu na ścinanie - odcinek I-ego rodzaju
CRd.c
0.18
γC
0.129
=
:=
współczynnik (pkt 6.2.2. str.78 EC2)
k
min 1
200mm
dp
+
2
,
1.357
=
:=
współczynnik (pkt 6.2.2. str.78 EC2)
ρL
min
AsL
bw.red dp
0.02
,
0.020
=
:=
stopień zbrojenia podłużnego
k1
0.15
:=
współczynnik (pkt 6.2.2. str.78 EC2)
AcA
Acc 0.933 m
2
=
:=
pole przekroju przęsłowego
NEd
AcA
7.697 MPa
=
52

0.2 fcd
7.333 MPa
=
σcp
min
NEd
AcA
0.2 fcd
,
7.333 MPa
=
:=
wartość naprężeń ściskających
νmin
0.035 k
2
3
fck 28dni
(
)
MPa
1
2
MPa
0.318 MPa
=
:=
współczynnik (wzór 6.3.N pkt 6.2.2.
str.78 EC2)
Nośność elementu na ścinanie w elemencie nie wymagającym obliczenia zbrojenia na ścinanie.
VRd.c_a
CRd.c k
100
ρL
fck 28dni
(
)
MPa
1
3
MPa
k1 σcp
+
bw.red
dp
636.023 kN
=
:=
wartość obliczeniowa wytrzymałości na ścinanie (wzór
6.2.a pkt 6.2.2. str.78 EC2)
VRD.c_b
νmin k1 σcp
+
(
)
bw.red dp
(
)
467.561 kN
=
:=
minimalna wartość obliczeniowa wytrzymałości na
ścinanie (wzór 6.2.b pkt 6.2.2. str.78 EC2)
VRd.c
max VRd.c_a VRD.c_b
,
(
)
636.023 kN
=
:=
wartość obliczeniowa wytrzymałości na
ścinanie
θ
acot 2
( )
26.565 deg
=
:=
kąt nachylenia krzyżulców betonowych
σcw σcp
(
)
1
σcp
fcd
+
0
σcp
<
0.25fcd
if
1.25
0.25fcd σcp
<
0.5fcd
if
2.5
1
σcp
fcd
-
0.5fcd σcp
<
fcd
<
if
:=
σcw σcp
(
)
1.200
=
współczynnik redukcji wytrzymałości betonu
zarysowanego przy ścinaniu
σcw
1.2
:=
zb
0.9dp 1.413 m
=
:=
ramię sił wewnętrzych przekroju
ν
0.6
1
fck 28dni
(
)
250MPa
-
0.468
=
:=
współczynnik zmiejszający wytrzymałość betonu
zarysowanego przy ścinaniu (wzór 6.6.N pkt 6.2.2.
str. 80 EC2)
53

ν1
ν
0.468
=
:=
współczynnik zmiejszający wytrzymałość betonu
zarysowanego przy ścinaniu
nośność elementów na ścinanie ze
względu na nośność ściskanych
krzyżulców betonowych
VRd.max
σcw bw
zb
ν1
fcd
cot
θ
( )
tan
θ
( )
+
2793.264 kN
=
:=
VEd.red dp
( )
VRd.c
0.000
=
warunek niespełniony
VEd.red dp
( )
VRd.max
1.000
=
warunek spełniony
Na odcinku I-ego rodzaju przyjęto rozstaw strzmion ze względów konstrukcyjnych.
x
L
2
dp
-
VRd.c
VEd.red dp
( )
6.907 m
=
:=
zasieg odcinka I-ego rodzaju
VEd.red x
( )
514.718 kN
=
wartość obliczeniowa siły poprzecznej
VRd.c
VEd.red x
( )
514.718 kN
=
:=
xI
leff
2
3.8975m
-
8.602 m
=
:=
zasięg odcinka I-ego rodzaju
ϕs
8mm
:=
śrdnica strzemion
α
90deg
:=
kąt nachylenia strzemion
sst.prov
500mm
:=
przyjęty rozstaw strzemion
maksymalne rozstaw podłużny strzemion
sl.max
0.75dp 1 cot α
( )
+
(
)
1.178 m
=
:=
maksymalny zalecany rozstaw strzemion podłużny
(wzrór 9.6 pkt. 9.2.2. str. 143 EC2)
st.max
min 0.75dp 600mm
,
(
)
0.600 m
=
:=
maksymalny zalecany rozstaw strzemion poprzeczny
(wzrór 9.8 pkt. 9.2.2. str. 144 EC2)
sst.prov st.max
1.000
=
warunek spełniony
Przyjęto rozstaw strzemion na odcinku I-ego rodzaju s = 50cm
Wymiarowanie podciągu ze względu na ścinanie - odcinek II-ego rodzaju
Przyjęto ograniczenie napreżeń w strzemionach do 80% obliczeniowej granicy plastyczności
zbrojenia na ścinanie.
54

fywk
500MPa
:=
charakterystyczna granica plastyczności stali
fywd
420MPa
:=
obliczeniowa granica plastyczności stali
nst
4
:=
liczba cieć
Asw
nst
π ϕs
2
4
2.011 cm
2
=
:=
pole przekroju poprzecznego zbrojenia na ścinanie
sst.req
Asw
VEd.red dp
( )
zb
0.80
fywd
cot
θ
( )
18.969 cm
=
:=
Przyjęto rozstaw strzemion na odcinku II-ego rodzaju s = 18cm
KONIEC OBLICZEŃ
55

kNm
kN m
:=
N
newton
:=
m
4
1.000 m
4.000
=
MPa
10
6
N
m
2
:=
MPa
10
6
Pa
:=
kN
10
3
N
:=
m
2
1.000 m
2.000
=
kNm
kN m
:=
m
1.000 m
=
dni
day
:=
kPa
10
3
Pa
:=
cm
0.01 m
:=
kN
1000N
:=
kPa
kN
m
2
:=
GPa
10
9
Pa
:=
N
1N
:=
cm
4
1.000
10
8
-
m
4.000
=
MN
10
6
N
:=
g
9.807
m
s
2.000
=
MPa
1 10
6
Pa
:=
56

57

UWAGA: Jeżeli któryś
z warunków nie jest spełniony
należy ponownie przyjąć inne h.b
i ponownie obliczyć wszystko do
tego miejsca
58

59

60

61

cw i cv - oznaczenia z PN-B-03264:2002
Liczymy środek cieżkości
odłonek kanałów - patrz
rysunek poniżej ---> eo, emax
62

UWAGA:Wzór na nachylenia
trasy kabla jest przybliżeniem
UWAGA:Wzór na odgięcie
trasy kabla jest przybliżeniem
63

64

65

Pm0
Pm0
lkab
2
t
0
,
7875.937 kN
=
:=
66

67

68

znajdź długość płyt i oparcie
hHC265
265mm
:=
69

70

71

72

h0.n 530.000 mm
=
73

74

75

b
9.000 m
=
gbelki.1
21.67
kN
m
:=
gbelki.2
21.67
kN
m
:=
gstrop 3800.000 Pa
=
gnbs
10
kN
m
:=
gnb
4
kN
m
:=
gr
3
kN
m
2
:=
76

77

pr.I
...
pr.II
Δσpr.III
+
)
Δσpr.I
-
Δσpr.II
-
Δσpr.III
-
4.500
-
10
6
Pa
=
78

Pm0 x t
,
(
)
P0 ΔPμ x
( )
-
ΔPsl x
( )
-
ΔPc x t
,
(
)
-
:=
Pm0
lkab
2
t
0
,
7875.937 kN
=
79

t
0
21.000 dni
=
80

81

82

83

Mnd 3607.692 kN m
=
84

85
Wyszukiwarka
Podobne podstrony:
Mathcad Projekt metal
Mathcad projekt
Mathcad Projekt wytrzymałość II cz 3
Mathcad projekt fund
Mathcad projekt 13
Mathcad Projekt 10 3 xmcd
Mathcad, projekt nr 1c
Mathcad PROJEKT drewno 2
Mathcad projekt 3
(Mathcad Projekt końcowy ppi
Mathcad Projekt 10 2 xmcd
Mathcad Projekt mostu sprężanego
Mathcad projekt 1 dwuteownik
Mathcad projekt edzia
Mathcad Projekt
Mathcad projekt 22
Mathcad, Projekt 10 3.xmcd
więcej podobnych podstron