POLITECHNIKA ŁÓDZKA

WYDZIAŁ BU DOWNICTWA, AECHITE KTURY

I INŻYNIERII ŚRODOWISKA

Kierunek: Budownictwo

Rok akademicki: 2009/2010

Rok II sem. IV

PROJEKT 1: NOŚNOŚĆ DWUGAŁĘZIOWEGO SŁUPA Z

PRZEWIĄZKAMI ŚCISKANEGO OSIOWO.

Wykonała: Edyta Kusideł

Dane:

Długość słupa:

L

6.1m



Obliczeniowa siła podłużna:

NEd

690kN



Gatunek stali:

S275

fy

275

N

mm

2



Granica plastyczności

M0

1



M1

1



Współczynniki częściowe:

Moduł sprężystości:

E

210000

N

mm

2



Długości wyboczeniowe:

Lcr.y

M0 L



6.1 m





Lcr.z

M1 L



6.1 m





Dobrany przekrój poprzeczny:

Przekrój poprzeczny

2xC180

wysokość przekroju gałęzi:

h

180mm



szerokość stopki

bf

70mm



tf

11mm



grubość stopki

grubość środnika

tw

8mm



promień zaokrąglenia

r

11mm



pole powieszchni

Ach

28cm

2



Iy.ch

1350cm

4



momenty bezwładności

Iz.ch

134cm

4



iy.ch

6.95cm



promienie bezwładności

iz.ch

2.02cm



wskaźnik sprężysty przekroju

Wz.el.ch

22.4cm

3



rozstaw osiowy gałęzi

h0

261.6mm



Gałęzie słupa połączono ze
sobą przewiązkami z blachy
płaskiej o przekroju

b

150mm



t

10mm



Przyjęto 4 przewiązki pośrednie
rozstawione w odstępach co

a

L

5

1.22 m





Wszystkie obliczenia zostały przeprowadzone zgodnie z norma PN-EN 1993-1-1

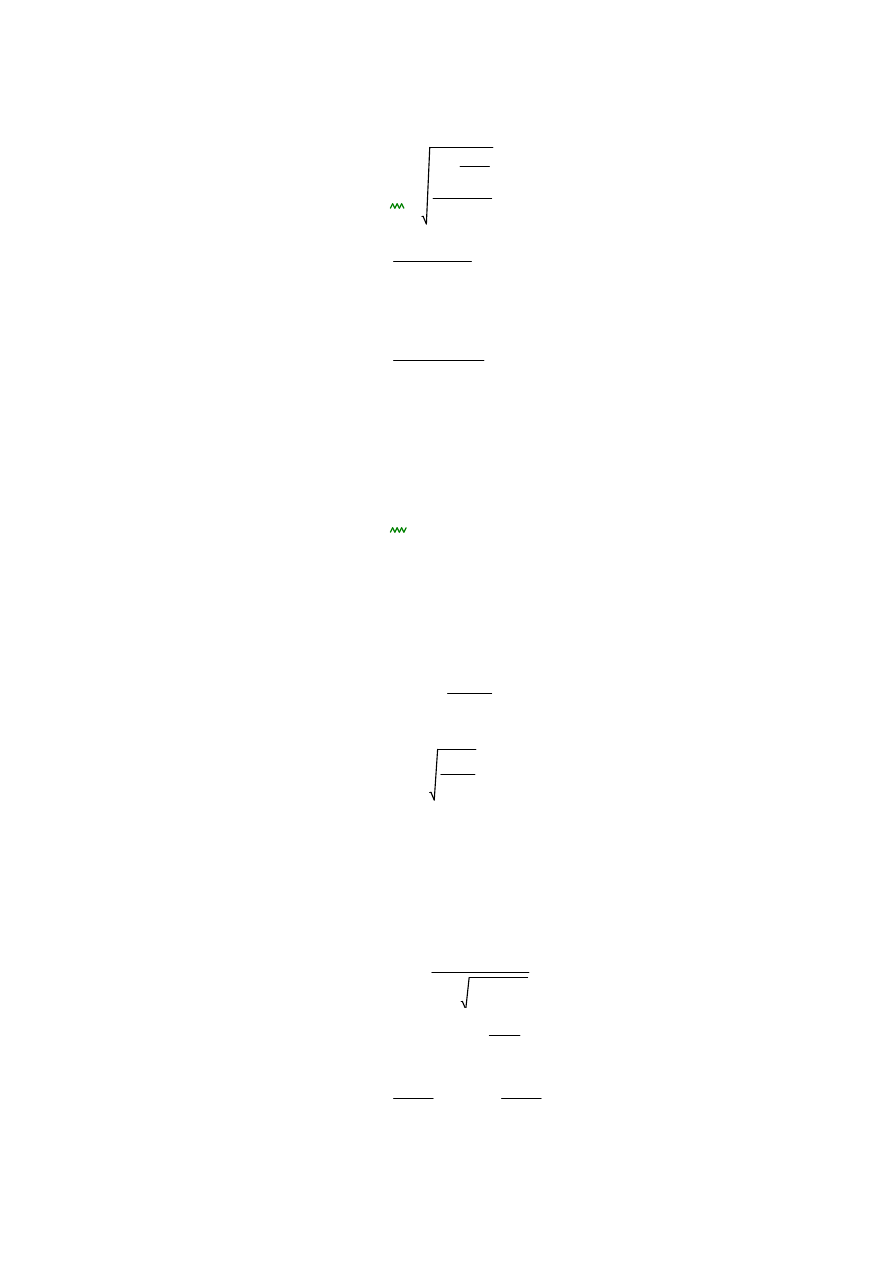
Klasa przekroju

Współczynnik

235

N

mm

2

fy

0.924





28.39

33



33

30.506



Stosuenk szerokości
do grubości środnika

h

2tf



2r



tw

17



28.393

38



38

35.128



środnik jest klasy 2 (przy ściskaniu)

Stosuenk szerokości
do grubości stopki

bf

tw



2r







2tf

1.818



4.141

38



38

35.128



stopki są klasy 1 (przy ściskaniu)

Wniosek : przy równomiernym ściskaniu przekrój jest klasy 2

Nośność obliczeniowa śłupa ze względu na wyboczenie względem osi y-y

Pole powierzchni przekroju
złożonego

A

2 Ach



5.6

10

3





m

2





Moment bezwładności przekroju
złożonego względem osi y-y

Iy

2Iy.ch

2.7

10

5





m

4





Promień bezwładności przekroju
złożonego względem osi y-y

iy

iy.ch 0.07 m





Siła krytyczna przy sprężystym
wyboczeniu giętnym słupa
dwugałęziowego wzg. osi y-y

Ncr.y

2

E Iy



Lcr.y

2

1.504

10

6



N





Smukłość względna przy
sprężystym wyboczeniu
giętnym

y

A fy



Ncr.y

1.012





Stosowany przekrój to dwuteownik walcowany, o proporcjach h/b>1,2 i maksymalnej
grubości ścianek t<40mm. W tym przypadku współycznnik wyboczenia giętnego
względem osi y-y przyjmuje się według krzywej a

Parametr imperfekcji

0.21



0.5 1

y

0.2











y

2













1.097





y

1

2

y

2





0.657





Współczynnik wyboczenia
giętnego

Nośność na wyboczenie

Nb.Rd

y A



fy

M1



1.012

10

6



N





Warunek nośności słupa przy
wyboczeniu względem osi y-y

NEd

Nb.Rd

0.682



NEd

Nb.Rd

1



warunek spełniony

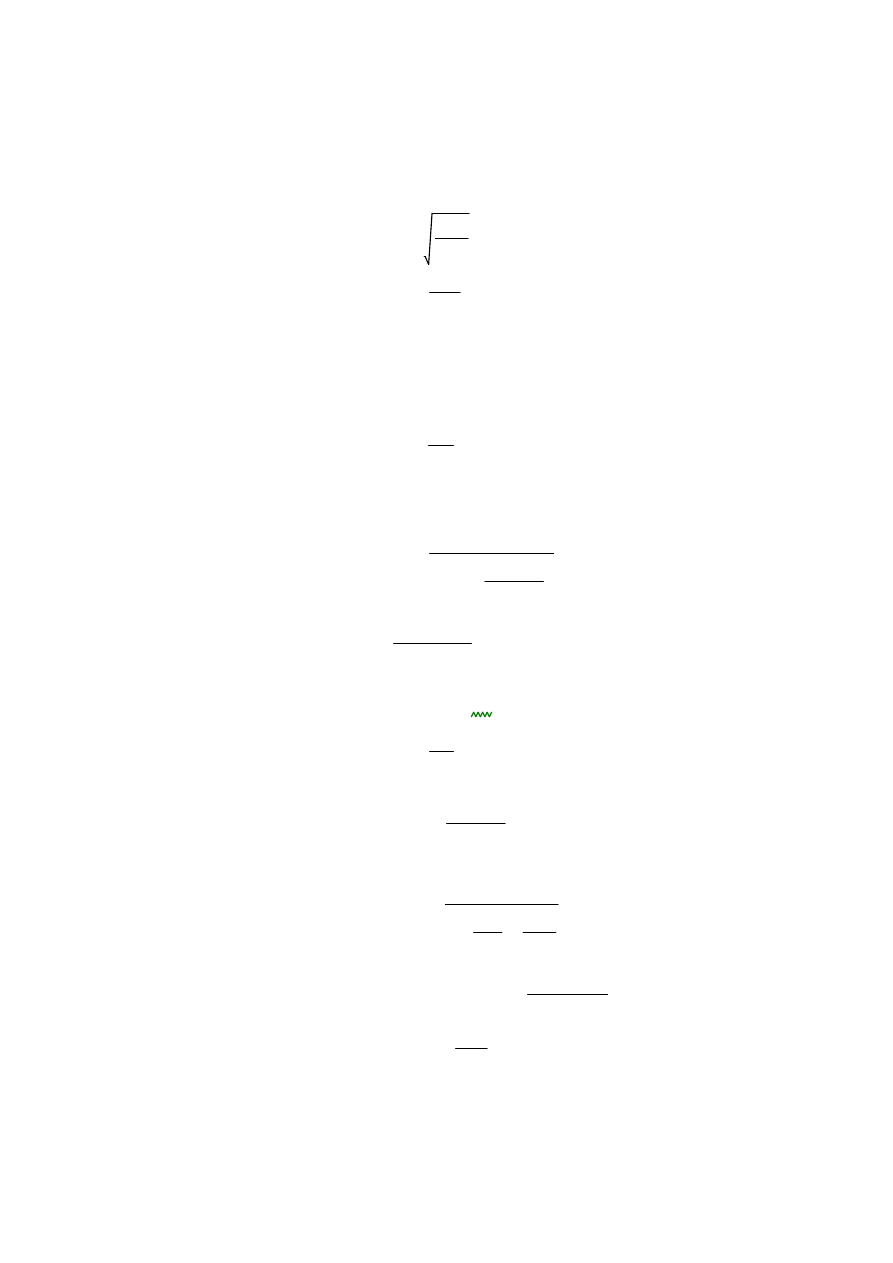
Nośność obliczeniowa śłupa ze względu na wyboczenie względem osi y-y

Moment bezwładności przekroju
złożonego względem osi z-z

Iz

0.5 h0

2



Ach



2 Iz.ch





9.849

10

5





m

4





Promień bezwładności przekroju
złożonego względem osi z-z

iz

Iz

2Ach

0.133 m





Smukłość giętna słupa przy
wyboczeniu względem osi z-z

z

Lcr.z

iz

45.997





54.892

75



Wskaźnik efektywności

1



Zastępczy moment
bezwładności

Ieff

0.5 h0

2



Ach



2

Iz.ch





9.849

10

5





m

4





Moment bezwładności jednej
przewiązki w płaszczyźnie
układu

Ib

b

3

t



12

2.813

10

6





m

4





Liczba płaszczyzn przewiązek

n

2



Sv

24 E



Iz.ch



a

2

1

2Iz.ch h0



n Ib



a

















4.117

10

6



N





Sztywność postaciowa słupa

2

2



E



Iz.ch



a

2

3.732

10

6



N



3.732 10

6



Sv



Przyjęto

Sv

3.732 10

6

N





Wstępna imperfekcja słupa

e0

L

500

0.012 m





Siła krytyczna wyboczenia
giętnego słupa dwugałęziowego
względem osi z-z

Ncr.z

2

E



Ieff



Lcr.z

2

5.486

10

6



N





Maksymalny moment przęsłowy
słupa z uwzględnieniem efektów
drugiego rzędu

MEd

NEd e0



1

NEd

Sv



NEd

Ncr.z



1.221

10

4



N·m





Obliczeniowa siła w pasie

Nch.Ed

0.5 NEd



MEd h0



Ach



2Ieff



3.904

10

5



N





Siła poprzeczna w słupie

VEd

MEd

L



6.289

10

3



N





Siła poprzeczna w pasie

Vch.Ed

0.5 VEd



3.145

10

3



N





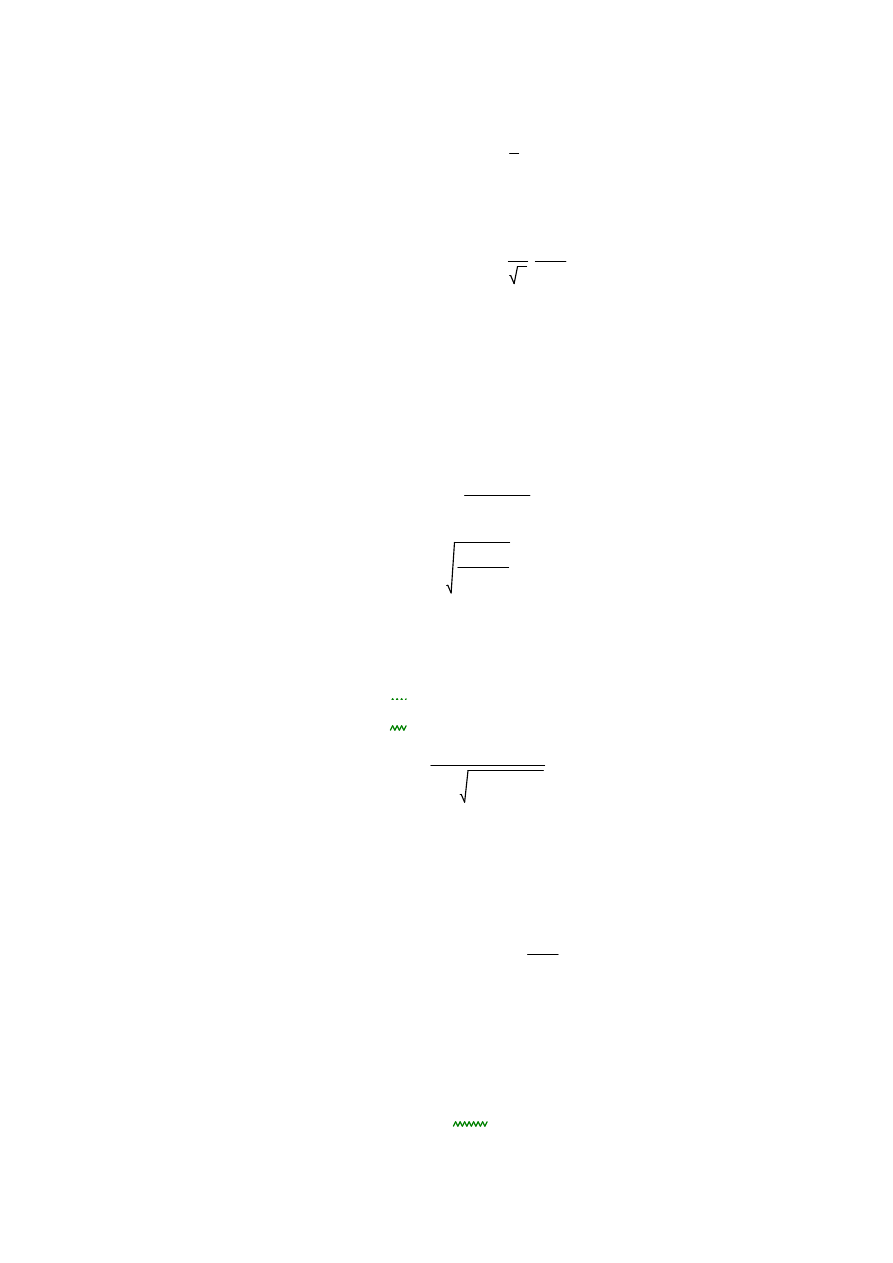
Moment zginający pas

Mch.Ed

Vch.Ed

a

2



1.918

10

3



N·m





Pole przekroju czynne przy
ścianiu jednego pasa

Ach.V

2 bf



tf



1.54

10

3





m

2





Nośność przekroju przy
ścinaniu jednego pasa

Vpl.Rd.z

Ach.V

fy

3



1

M0



2.445

10

5



N





Wpływ tnącej na nośność przekroju przy zginaniu może być pominięty, ponieważ siła
tnąca nie przekracza 50% nośności plastycznej przekroju przy ścinaniu

Vch.Ed 3.145 10

3



N



Vch.Ed Vpl.Rd.z



Vpl.Rd.z 0.5



1.223

10

5



N



Sprawdzenie warunku nośności pojedynczej gałęzi słupa ściskanej i zginanej
względem osi z-z

Siła krytyczna przy wyboczeniu
giętnym pojedynczej gałęzi
słupa względem osi z-z

Ncr.ch.z

2

E



Iz.ch



a

2

1.866

10

6



N





Smukłość względna pojedynczej
gałęzi przy wyboczeniu giętnym
w przedziale między
przewiązkami

ch.z

Ach fy



Ncr.ch.z

0.642





Stosowany przekrój to dwuteownik walcowany, o proporcjach h/b>1,2 i maksymalnej
grubości ścianek t<40mm. W tym przypadku współycznnik wyboczenia giętnego
względem osi z-z przyjmuje się według krzywej b

Parametr imperfekcji

0.34



0.5 1

ch.z

0.2











ch.z

2













0.782





z

1

2

ch.z

2





0.815





Współczynnik wyboczenia
giętnego

Nośność przekroju przy zginaniu

Jeżeli przy równomiernym ściskaniu przekrój jest klasy 2, to przy zginaniu względem osi
z-z przekrój również jest klasy 2. Wskaźnik plastyczny obliczono przyjmując mnożnik 1.5
do wskaźnika sprężystego przekroju dwuteowego.

Wskaźnik plastyczny

Wz.pl.ch

1.5 Wz.el.ch



3.36

10

5





m

3





Nośność przekroju przy
zginaniu względem osi z-z

Mc.Rd.ch

Wz.pl.ch

fy

M0



9.24

10

3



N·m





Wykres momentu zginającego pas na odcinku między przewiązkami zmienia się linowo
od wartości +Mch,Ed do - Mch,Ed. Stosunek momentów na końcach elementu ψ=-1.
Współczynniki interakcyjne obliczone zostały Metodą 2 (załącznik B PN-EN 1993-1-1)

1





Cmz

0.6

0.4



0.2





Cmz 0.4



Przyjęto Cmz

0.4



Współczynnik interakcji

kzz

Cmz 1

2 ch.z 0.6







Nch.Ed

z Ach



fy

M1

























0.57





Cmz 1 1.4

Nch.Ed

z Ach



fy

M1

























0.748



Przyjęto

kzz

0.57



Nośność przekroju na zginanie

Nc.Rd.ch

fy

Ach

M0



7.7

10

5



N





Warunek nośności elementu ściskanego i zginanego

Nch.Ed

z

Nc.Rd.ch

M1



kzz

Mch.Ed

Mc.Rd.ch

M1





0.74



0.74

1



Warunek spełniony

Sprawdzenie nośności przewiązki

Przewiązka obciążona jest siłą
tnącą i momentem zginającym
o wartościach

Vb.Ed

VEd a



2 h0



1.467

10

4



N





Mb.Ed

VEd a



4

1.918

10

3



N·m





Pole powieszchni przewiązki

Ab

t b



1.5

10

3





m

2





Wel

b

2

t

6



3.75

10

5





m

3





Wskaźnik sprężysty przewiązki

Nośność przy ścinaniu

Vpl.Rd

Ab

fy

3

M0





2.382

10

5



N





Vb.Ed 1.467 10

4



N



Vb.Ed 0.5 Vpl.Rd.z





0.5 Vpl.Rd



1.191

10

5



N



Warunkek spełniony

Nośność przy zginaniu

Mc.Rd

Wel

fy

M0



1.031

10

4



N·m





Warunki nośności

Vb.Ed

Vpl.Rd

0.062



Vb.Ed

Vpl.Rd

1



Warunki spełnione

Mb.Ed
Mc.Rd

0.186



Mb.Ed
Mc.Rd

1



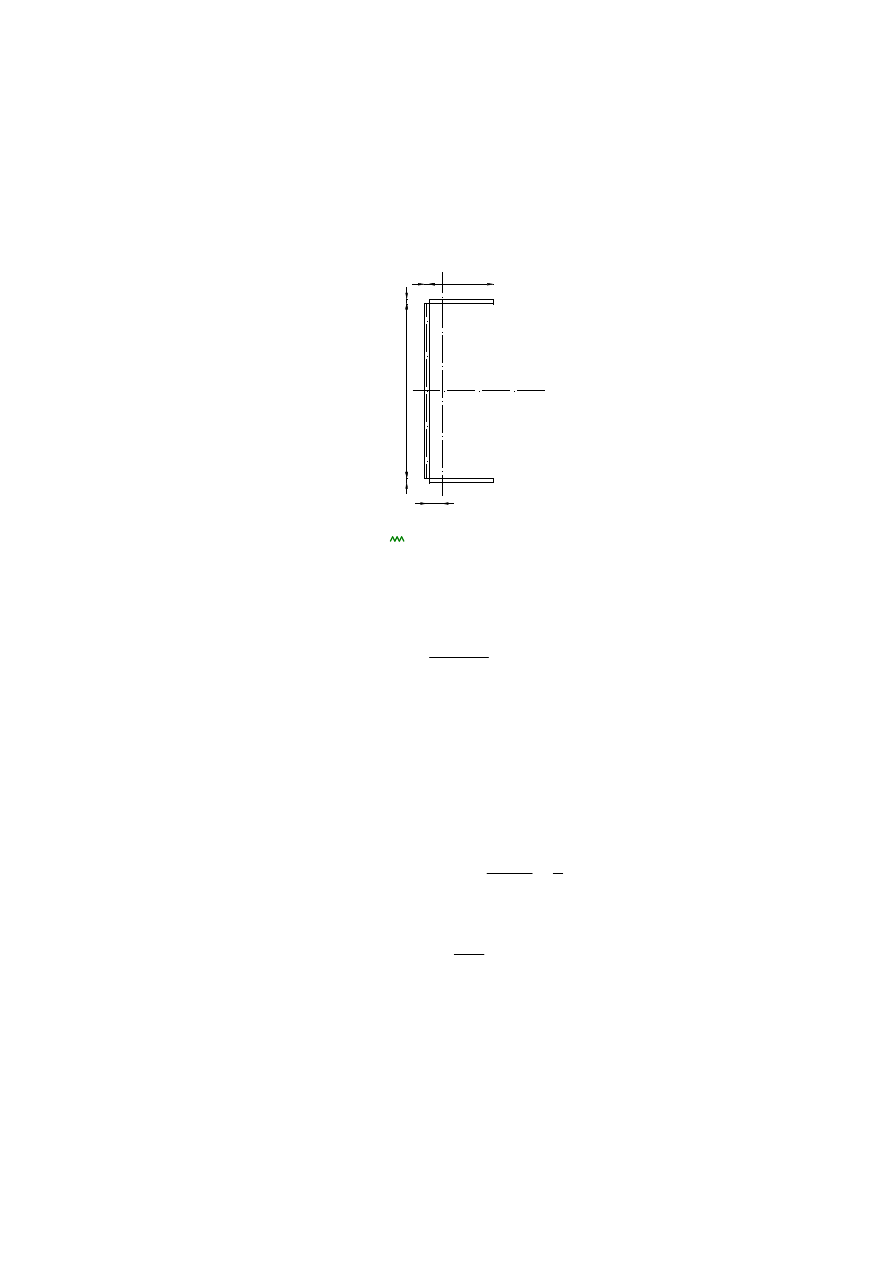
Sprawdzenie nośności spoiny łączącej przewiązkę z gałęzią słupa

Przewiązka połączona jest z gałęzią słupa spoiną pachwinową o kładzie przedstawionym
poniżej. Przyjęto spoinę o grubości a=4mm. Wymiarowanie spoiny wykonano przy
założeniu plastycznego rozkładu naprężeń.

b

a

a

d

yc

a

y

z

C

a

4mm



Grubość spoiny

d

0.5 250mm

h0



bf









0.029 m





b

0.15 m



Cechy geometryczne kładu spoin

Położenie środka ciężkości

yc

d a

d



(

)



2d

b



4.652

10

3





m





Pole powierzchni spoiny
pionowej

AV

a b



6

10

4





m

2





Pole powierzchni spoiny
poziomej

AH

a 2

 d

2.336

10

4





m

2





Obciążenie spoiny

Siła ścinająca

Vb.Ed 1.467 10

4



N



Moment skręcający

MT

Vb.Ed

250mm

2

a

2



yc

















1.794

10

3



N·m





Wytrzymałość spoiny
(przyjęto jak stali gałęzi S355)

fu

430

N

mm

2



Współczynnik częściowy

M2

1.25



Współczynnik koreacji

w

0.85



Wymiarowanie przy założeniu plastycznego rozkładu naprężeń

Przyjęto, że moment skręcający zostanie przeniesiony przez parę sił P działających
wzdłuż części poziomych spoin oraz, że siła tnąca zostanie przeniesiona przez część
pionową

P

MT

a

b



1.165

10

4



N





Naprężenie styczne w spoinach
poziomych

2

P

AH



9.975

10

7



Pa





Warunek nośności spoiny

3



1.728

10

8



Pa



3



fu

w M2





fu

w M2



4.047

10

8



Pa



Warunek spełniony

Naprężenie styczne w spoinie
pionowej

Vb.Ed

AV

2.444

10

7



Pa





Warunek nośności spoiny

3



4.234

10

7



Pa



3



fu

w M2





fu

w M2



4.047

10

8



Pa



Warunek spełniony