kNm
kN m
:=
1. Geom etria stropu
Rozpietość belek stropowych:
B
7.8m
:=
Rozstaw belek stropowych:
a
2.3m
:=
Liczba belek:
n
7
:=
Rozpietość dźwigarów:
L
n a
16.1 m
=
:=
2. Zebranie obciążeń - belka stropowa
1. Obciążenia stałe: ciężar płyty 12cm, ciężar wartsw wykończeniowych 0,3 kN/m 2,
ciężar własny belki IPE400
2. Obciążenia zmienne: obciążenie użytkowe 3,7 kN/m 2
3. Obliczenia belki stropowej
1. Warunek nośności belki przy zginaniu,
2. Warunek nośności przekroju przy ścinaniu,
3. Sprawdzenie ugięć granicznych,
4. Warunk i nośności belki w mi ejscu połacz enia z dźwigarem .
3.1 Warunek nośności belk i przy zginaniu
Moment zginający w belce:
My.Ed
156kNm
:=
Przekrój: dwuteownik równoległościenny IPE400 ze stali S235
Wysokość
h
400mm
:=
Szerokość
b
180mm
:=
Grubość części
tf
13.5mm
:=
tw
8.6mm
:=
Promień zaokrąglenia
r
21mm
:=
Szerokość środnika
hw
h
2 tf
-
0.373 m
=
:=
Granica plastyczności
fy
275MPa
:=
ε
1
:=
Współczynniki częściowe
γM0
1.0
:=
γM1
1.0
:=
Klasa przekroju:
środnik:
h
2 r
-
2 tf
-
tw
38.488
=
72
ε
72
=
stopka:
b
tw
-
2 r
-
2 tf
4.793
=
9
ε
9
=
Przekrój przy zginaniu jest klasy 1.
Wskaźnik plastyczny przekroju:
Wpl.y
b tf
h
tf
-
(
)
hw
2
tw
4
+
2 r
2
hw r
-
(
)
+
π r
2
hw
2
4
3
π
-
3
π
r
+
-
1.307 L
=
:=
Nośność plastyczna przekroju:
Mc.y.Rd
Wpl.y fy
γM0
3.595
10
5
J
=
:=
Belka pasem górnym (ściskanym) jest stężona bocznie na całej długości.
Pom inieto zwichrzenie.
χLT
1
:=
Nośność zwichrzeniowa belki:
Mb.y.Rd
χLT
Wpl.y fy
γM1
3.595
10
5
J
=
:=
Warunek stateczności elementu:
My.Ed
Mb.y.Rd
0.434
=
0.434
1
<
Warunek spełniony.
3.2 Warunek nośności przek roju przy ścinaniu
Siła tnąca przy podporze:
Vz.Ed
80kN
:=
Sprawdzenie wrażliwości na m iejscową utratę stateczności
współczynnik:
η
1.2
:=
środnik:
hw
tw
43.372
=
72
ε
η
60
=
Środnik nie jest wrażliwy na utratę stateczności miejscowej.
Pole przekroju brutto:
A
2 tf
b
h
2 tf
-
(
)
tw
+
4
π
-
(
) r
2
+
8.446
10
3
-
m
2
=
:=
Pole czynne przy ścinaniu:
AV
max A
2 b
tf
-
tf 2 r tw
+
(
)
+
η hw
tw
,
4.269
10
3
-
m
2
=
:=
Nośność plastyczna przekroju:
Vc.z.Rd
AV fy
3
γM0
6.779
10
5
N
=
:=
Warunek wytzrymałości przekroju:
Vz.Ed
Vc.z.Rd
0.118
=
0.118
1
<
Warunek jest spełniony.
3.3 Sprawdzenie ugięć granicznych
Ugięcie belki w środku rozpietości:
wmax
15.5mm
:=
Ugięcie dopuszcalne belki:
B
250
0.031 m
=
Warunek jest spełniony.
3.4 Warunki nosności belki w miejscu połąc zeni a z dźwi garem
Reakcja podporowa belki:
R
Vz.Ed 8 10
4
N
=
:=
Połączenie zakładkowe dociskowe (kat. A). Przyj ęto 2 śruby M16 kl. 8.8
Siła tnąca na jeden łącznik:
FEd
R
2
4
10
4
N
=
:=
Nośność śruby na ścinanie:
Fv.Rd
0.6 161
mm
2
800
MPa
1.25
6.182
10
4
N
=
:=
FEd
Fv.Rd
0.647
=
0.647
1
<
Warunek jest spełniony.
Nośność otworu na docisk:
αd
40mm
3 18
mm
0.741
=
:=
αb
min 1
αd
,
(
)
0.741
=
:=
k1
min 2.5 2.8
40mm
18mm
1.7
-
,
2.5
=
:=
t
tw 8.6 10
3
-
m
=
:=
d
16mm
:=
Fb.Rd
k1 αb
d
t
360
MPa
1.25
7.339
10
4
N
=
:=
FEd
Fb.Rd
0.545
=
0.545
1
<
Warunek jest spełniony.
Rozerwanie blokowe:
An.t
40mm
d
2
-
tw
2.752
10
4
-
m
2
=
:=
An.v
40mm
110mm
+
d
-
d
2
-
tw
1.084
10
3
-
m
2
=
:=
Feff.1.Rd
An.v 235
MPa
3 1.0
An.t 360
MPa
1.25
+
2.263
10
5
N
=
:=
R
Feff.1.Rd
0.354
=
0.354
1
<
Warunek jest spełniony.
Złożony stan naprężenia w m iejscu podcięcia:
R
8
10
4
N
=
M1
R 110
mm
8.8
10
3
J
=
:=
h1
h
40mm
-
:=
b1
b
2
tw
2
-
0.086 m
=
:=
zc
0.5 h1
2
tw
0.5 tf
2
b1
+
h1 tw
b1 tf
+
0.133 m
=
:=
Iy
h1
3
tw
tf
3
b1
+
12
h1 tw
zc
-
h1
2
+
2
+
b1 tf
zc
-
tf
2
+
2
+
5.873
10
5
-
m
4
=
:=
Wy
Iy
h1 zc
-
0.259 L
=
:=
τ
R
h1 tw
2.584
10
7
Pa
=
:=
σ
M1
Wy
3.403
10
7
Pa
=
:=
σred
σ
2
3
τ
2
+
5.622
10
7
Pa
=
:=
fy
γM0
2.75
10
8
Pa
=
σred
fy
γM0
<
Warunek jest spełniony.
4. Obliczenia dźwigara
1. Warunek nośności dźwigara przy zginaniu,
2. Warunek nośności przekroju przy ściananiu,
3. Sprawdzenie ugięć granicznych,
4. Dobór żeber ze względu na ścinanie,
5. Połaczenie dźwigara ze słupem.
4.1 Warunek nośności dźwigara przy zginaniu
Moment zginający w dźwigarze:
My.Ed
2381kN
:=
Przekrój: dwuteownik spawany 1300x10/300x18 ze stali S275
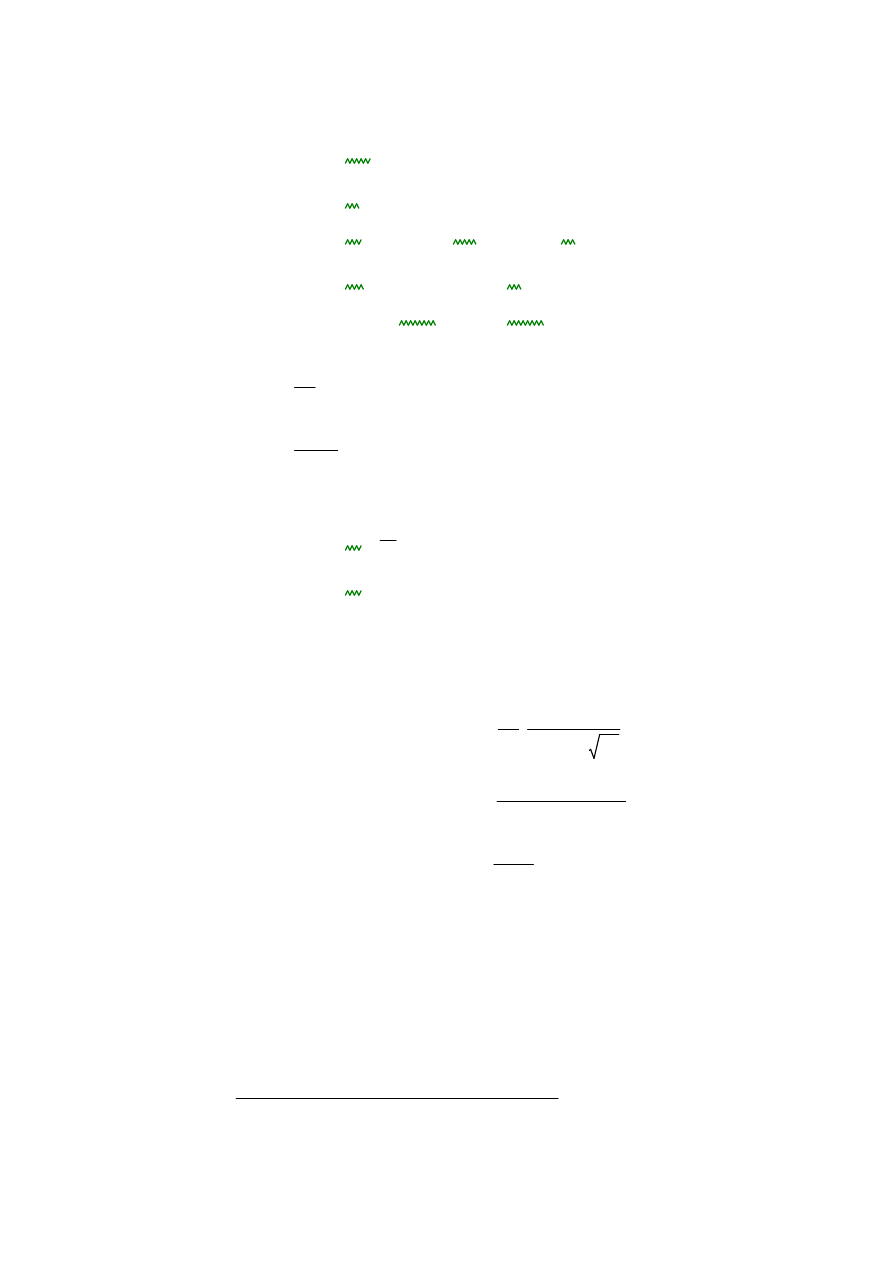
Wysokość środnika:
hw
1300mm
:=
Szerokość:
b
300mm
:=
Grubość części:
tf
18mm
:=
tw
10mm
:=
h
hw 2 tf
+
:=
Granica plastyczności:
fy
275MPa
:=
ε
0.924
:=
Współczynniki częściowe:
γM0
1.0
:=
γM1
1.0
:=
Klasa przekroju
środnik
hw
tw
130
=
124
ε
114.576
=
130
114.576
>
stopka
b
tw
-
2 tf
8.056
=
9
ε
8.316
=
8.056
8.316
<
Przekrój przy zginaniu jest klasy 4, przy czym wrażliwy na utratę statecznosci jest tylko
środnik.
Cechy przekroju brutto:
Iy
1
12
h
3
b
h
2 tf
-
(
)
3
b
tw
-
(
)
-
6.521
10
3
-
m
4
=
:=
A
2 tf
b
h
2 tf
-
(
)
tw
+
0.024 m
2
=
:=
środnik
współczynnik rozkładu naprężeń norm alnych na szerokości ścianki:
Ψ
1
-
:=
parametr niestateczności m iejscowej:
kσ
23.9
:=
sm ukłość względna:
λw
hw
tw
1
28.419
ε
kσ
1.013
=
:=
współczynnik redukcyjny:
ρw
λw 0.055 3 Ψ
+
(
)
-
λw
2
0.88
=
:=
szerokość strefy ściskanej:
bc
hw
1
Ψ
-
0.65 m
=
:=
szerokości współpracujące:
beff
bc ρw
0.572 m
=
:=
be.1
0.4 beff
0.229 m
=
:=
be.2
0.6 beff
0.343 m
=
:=
zm iana polożenia środka ciężkości:
Δzc
tw bc beff
-
(
)
0.5 h
tf
-
be.1
-
0.5 bc
beff
-
(
)
-
A
tw bc beff
-
(
)
-
0.013 m
=
:=
Cechy przekroju współpracujacego:
Ieff.y=
Iy A Δzc
2
+
1
12
bc beff
-
(
)
3
tw
-
1
-
(
) tw
bc beff
-
(
)
0.5 hw
Δzc
+
be.1
-
0.5 bc beff
-
(
)
-
+
Ieff.y
6.403
10
3
-
m
4
:=
Weff.y
Ieff.y
0.5 h
Δzc
+
9.403 L
=
:=
Nośność plastyczna przekroju:
Mc.y.Rd
Weff.y fy
γM0
2.586
10
6
J
=
:=
My.Ed
Mc.y.Rd
0.921
1
m
=
0.921
1
<
Warunek jest spełniony.
Zwichrzenie - metoda uproszczona
Lc
2.3m
:=
Ψ
1610.3
2179.1
0.739
=
:=
kc
1
1.33
0.33
Ψ
-
0.921
=
:=
Iz.f
1
12
b
3
tf
1
72
hw
tw
3
+
4.052
10
5
-
m
4
=
:=
Af
b tf
1
6
hw
tw
+
7.567
10
3
-
m
2
=
:=
iz.f
Iz.f
Af
0.073 m
=
:=
λ1
93.9
ε
86.764
=
:=
λc.0
0.4
:=
λf
Lc kc
iz.f λ1
0.334
=
:=
λc.0
Mc.y.Rd
My.Ed
0.434 m
=
λf λc.0
Mc.y.Rd
My.Ed
<
Nie przekroczono granicznej wartości smukłości gietnej pasa pzry wyboczeniu z
płaszczyzny dźwigara. Warunek stateczności elementu sprowadza się do warunku
wytrzymałości pzrekroju. Warunek zat em jest spełni ony.
4.2 Warunek nośności dźwigara przy śc inaniu
Zastosowano żebra podporowe i pośrednie. Przy podporze przyjęto rozstaw obliczeniowy
1150m m, na długości przęsła 2300m m.
Panel środnika przy podporze:
a
1150mm
:=
hw
1300mm
:=
Siła tnąca przy podporze:
Vz.Ed.1
577kN
:=
Parametr niestatecznosci:
kτ
5.34
4
hw
a
2
+
10.452
=
:=
Sprawdzenie wrażliwości na m iejscową utratę stateczności:
hw
tw
130
=
31
kτ
ε
η
77.169
=
hw
tw
31
kτ
ε
η
>
Panel środnika jest wrażliwy na utratę stateczności przy ścinaniu.
Smukłość względna:
λw
hw
tw
1
37.4
ε
kτ
1.164
=
:=
Współczynnik redukcyjny niestatecznosci:
χw
1.37
0.7
λw
+
0.735
=
:=
Nośność wyboczeniowa środnika na ścinanie:
Vbw.Rd.1
χw hw
tw
fy
3
γM1
1.517
10
6
N
=
:=
Warunek nośności na ścinanie panela:
Vz.Ed.1
Vbw.Rd.1
0.38
=
0.38
1
<
Warunek jest spełniony.
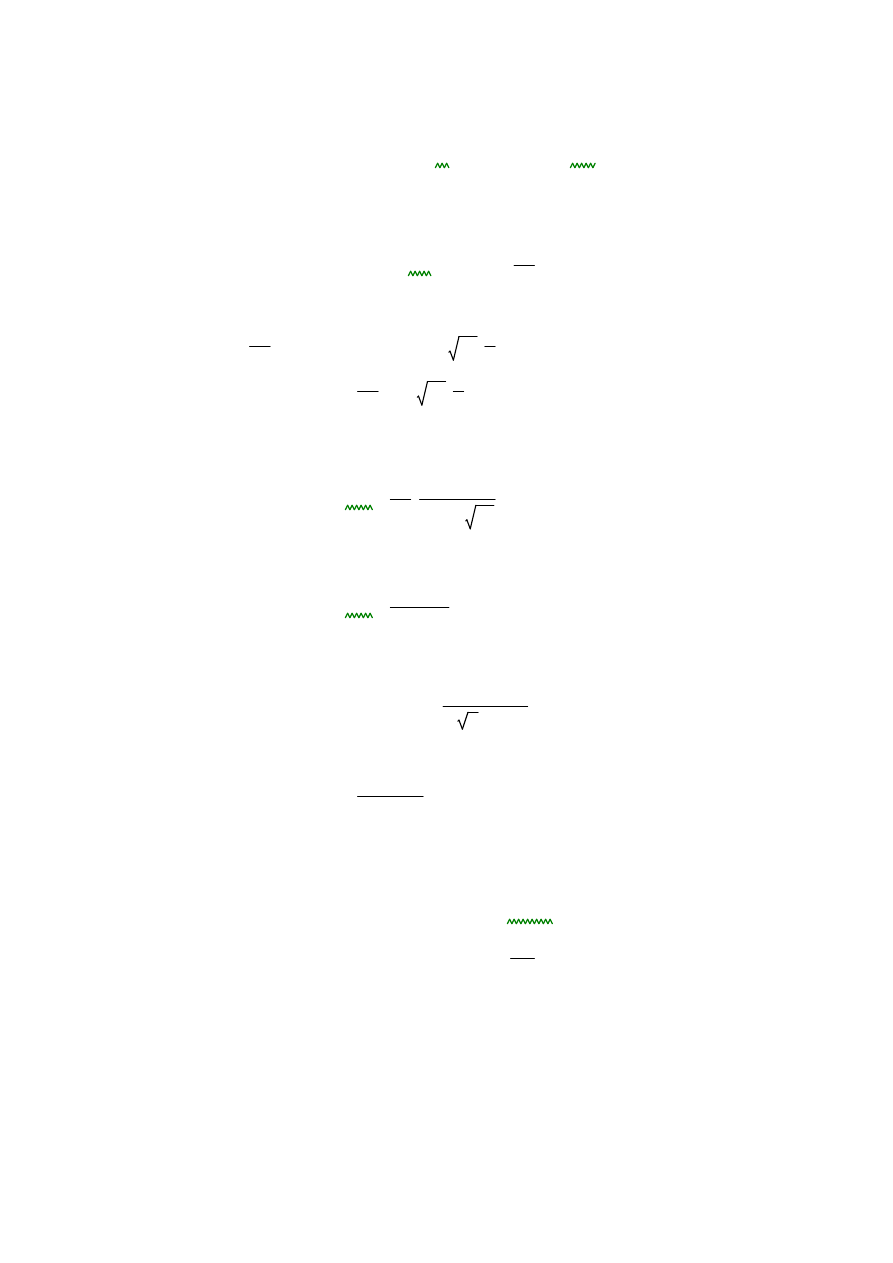
Panel środnika za pierwszą belką::
a
2300mm
:=
hw
1300mm
:=
Siła tnąca przy podporze:
Vz.Ed.2
415kN
:=
Parametr niestatecznosci:
kτ
5.34
4
hw
a
2
+
6.618
=
:=
Sprawdzenie wrażliwości na m iejscową utratę stateczności:
hw
tw
130
=
31
kτ
ε
η
61.406
=
hw
tw
31
kτ
ε
η
>
Panel środnika jest wrażliwy na utratę stateczności przy ścinaniu.
Smukłość względna:
λw
hw
tw
1
37.4
ε
kτ
1.462
=
:=
Współczynnik redukcyjny niestatecznosci:
χw
1.37
0.7
λw
+
0.634
=
:=
Nośność wyboczeniowa środnika na ścinanie:
Vbw.Rd.2
χw hw
tw
fy
3
γM1
1.308
10
6
N
=
:=
Warunek nośności na ścinanie panela:
Vz.Ed.2
Vbw.Rd.2
0.317
=
0.317
1
<
Warunek jest spełniony.
4.3 Sprawdzenie ugięć granicznych
Ugięcie dźwigara w środku rozpiętości:
wmax
35.2mm
:=
Ugięcie dopuszczalne dźwigara:
L
350
0.046 m
=
Warunek jest spełniony.
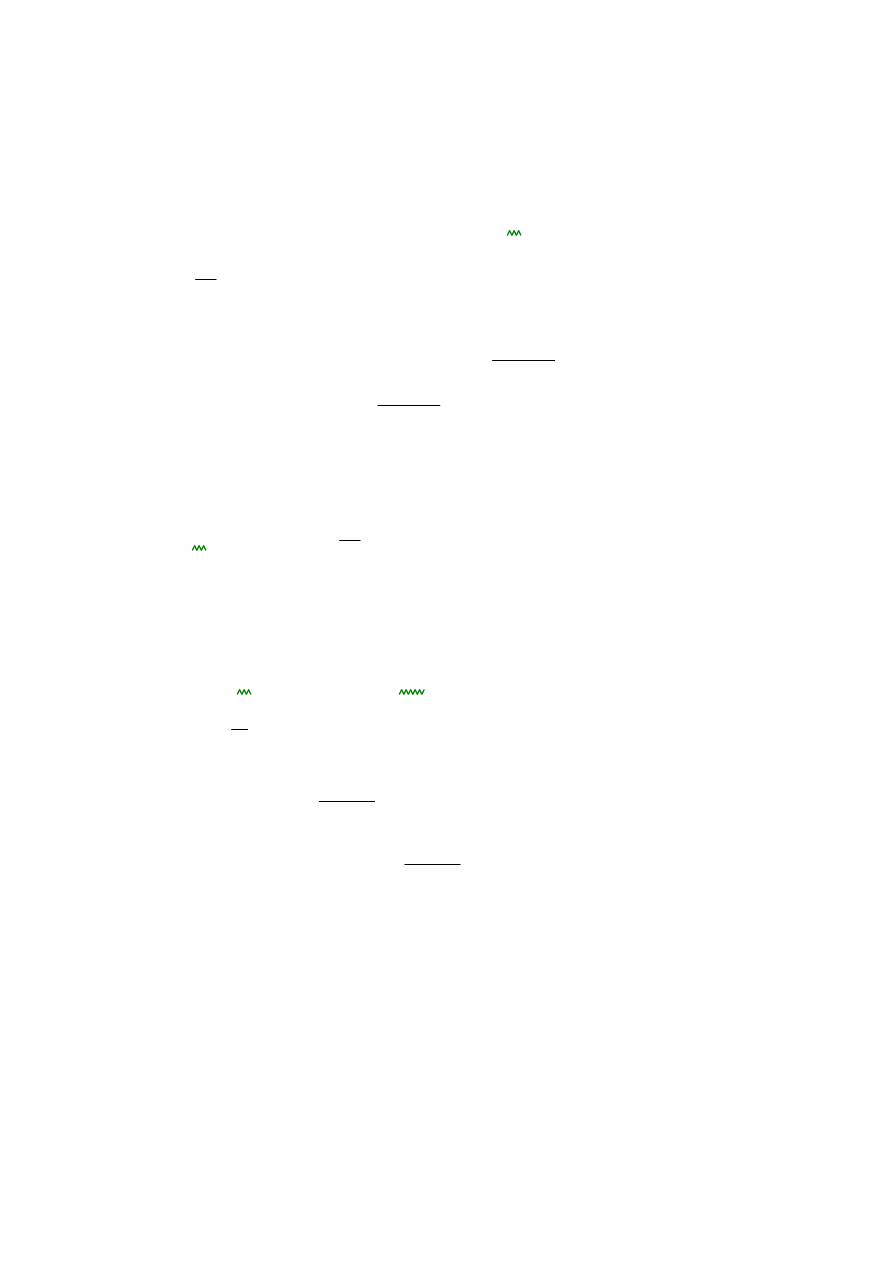
4.4 Dobór żeber ze wzgledu na ścinanie
Żebro podporowe sztywne
Żebro podporowe przyjęto jako zdwojone żebro dwustronne z płaskownika 150x10, w
odstępie osiowo 230mm
bst
150mm
:=
tst
12mm
:=
e
230mm
:=
bst
tst
12.5
=
14
ε
12.936
=
12.5
12.936
<
Żebro jest stateczne.
Ast
2 bst
tst
3.6
10
3
-
m
2
=
:=
4 hw
tw
2
e
2.261
10
3
-
m
2
=
Ast
4 hw
tw
2
e
>
Warunek jest spełniony.
e
230mm
:=
hw
10
0.13 m
=
230mm
130mm
>
Warunek jest spełniony.
Żebro przyjęto właściwie.
Żebro pośrednie sztywne
Przyjeto żebra pośrednie 150x10
a
1150mm
:=
hw
1300mm
:=
Ist
1
12
2 bst
tw
+
(
)
3
tst
2.5
ε
tw
4
+
2.981
10
5
-
m
4
=
:=
1.5
hw
3
tw
3
a
2
2.492
10
6
-
m
4
=
Ist 1.5
hw
3
tw
3
a
2
>
Warunek jest spełniony.
Żebro przyjęto właściwie.
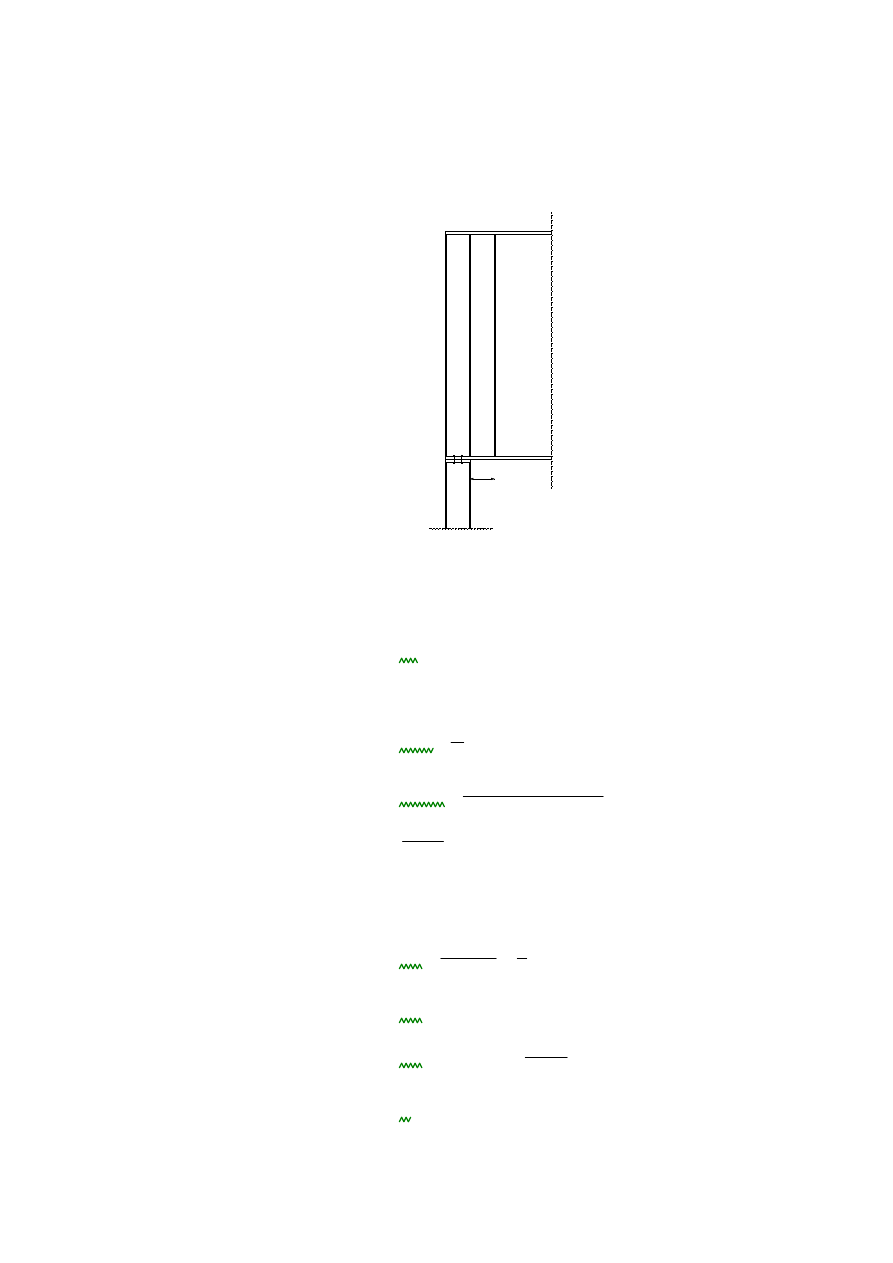
4.5 Połączenie dźwigara ze słupem
230
Reakcja podporowa dźwigara:
R
Vz.Ed.1 5.77 10
5
N
=
:=
Połączenie zakładkowe dociskowe (kat. A).
Przyjęto 8 śrub M20 kl. 8.8, co 100mm
Siła tnąca na jeden łącznik:
FEd
R
8
7.213
10
4
N
=
:=
Nośność śruby na ścinanie:
Fv.Rd
0.6 245
mm
2
800
MPa
1.25
9.408
10
4
N
=
:=
FEd
Fv.Rd
0.767
=
0.767
1
<
Warunek jest spełniony
Nośność śruby na docisk:
αd
100mm
3 18
mm
1
4
-
1.602
=
:=
αb
min 1
αd
,
(
)
1
=
:=
k1
min 2.5 2.8
40mm
18mm
1.7
-
,
2.5
=
:=
t
tw 0.01 m
=
:=
d
20mm
:=
Fb.Rd
k1 αb
d
t
360
MPa
1.25
1.44
10
5
N
=
:=
FEd
Fb.Rd
0.501
=
0.501
1
<
Warunek jest spełniony.
2