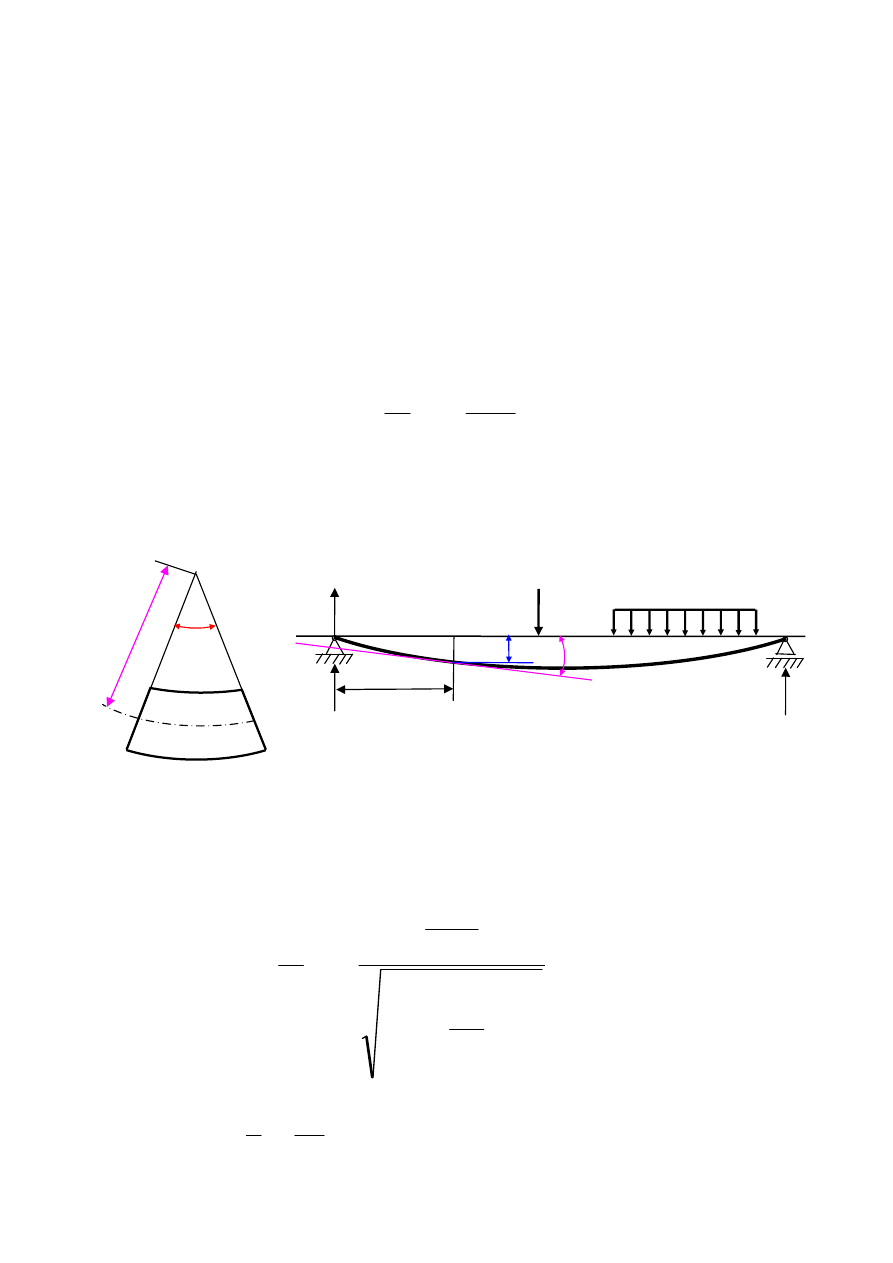
1

RÓWNANIE RÓŻNICZKOWE OSI UGIĘTEJ BELKI

W wyniku działania momentu gnącego zachodzi wzajemny obrót względem

osi obojętnej uprzednio równoległych przekrojów (rys 1.a). Odkształcenia te po-

wodują zakrzywienie, czyli ugięcie prostej osi pręta. W układzie prostokątnym w

którym oś x pokrywa się z nieodkształconą osią pręta (rys 1.b), oś ugiętą określa

równanie osi ugiętej

y

f x

=

( )

, jej krzywiznę natomiast wyraża wzór (1).

EI

Mg

−

=

ρ

1

(1)

Wzór powyższy nie uwzględnia wpływu siły poprzecznej, ponieważ jej wpływ w
większości zagadnień technicznych jest znikomy.

Rys 1.

Z analizy różniczkowej krzywiznę dowolnej krzywej płaskiej

y

f x

=

( )

przedsta-

wia równanie

3

2

2

2

1

1



























+

±

=

dx

dy

dx

y

d

ρ

(2)

podstawiając

EI

Mg

−

=

ρ

1

otrzymuje się

y

x

R

1

R

2

q

F

θ

y

ρ

d

ϕ

ds=dx

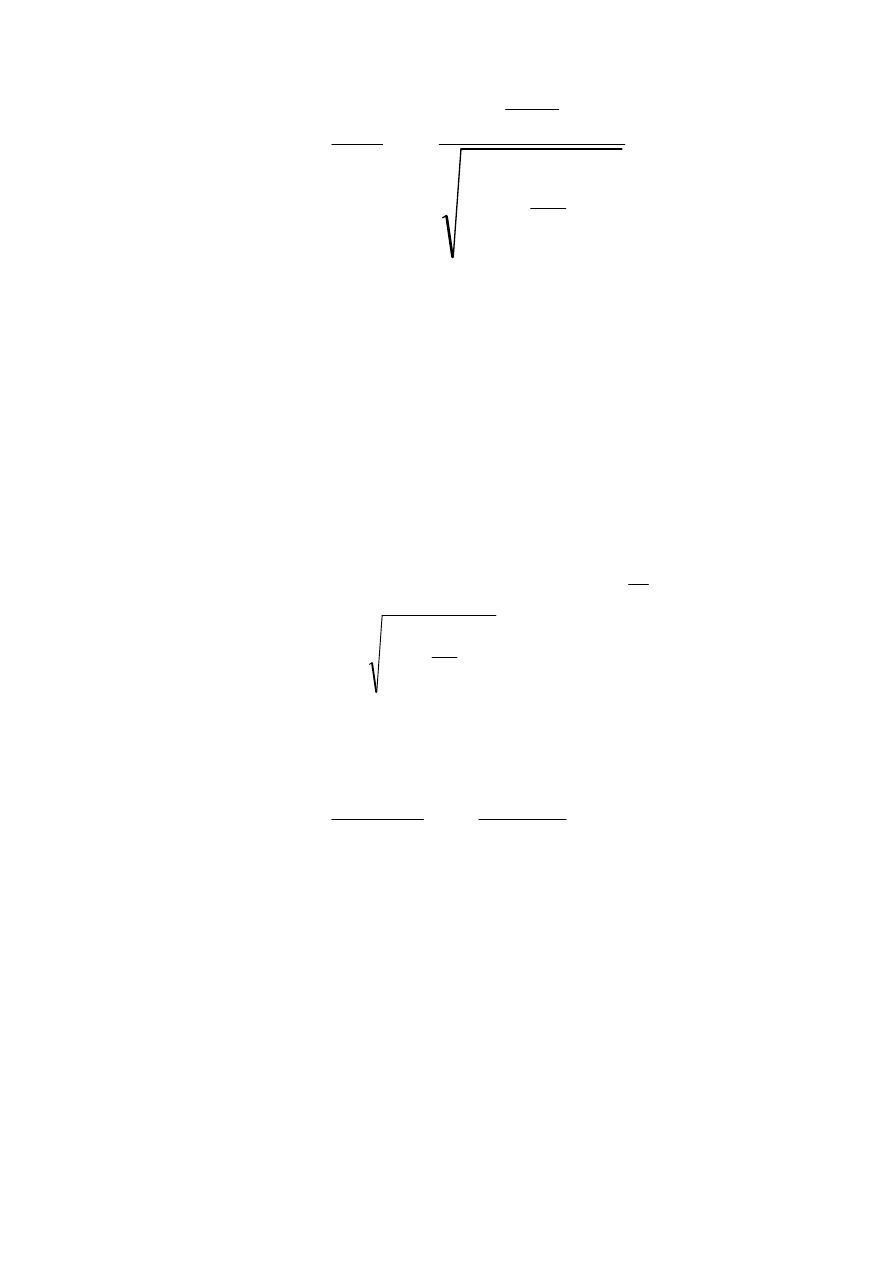
2

Mg

EI

d y

dx

dy

dx

= ±

+



























2

2

2

3

1

(3)

Jest to równanie osi ugiętej w postaci różniczkowej

W praktyce inżynierskiej - duża sztywność prętów - odkształcenia małe, promienie

krzywizny bardzo duże w wyniku czego przemieszczenia liniowe

y

f x

=

( )

oraz

przemieszczenia kątowe

y

f x

'

'

( )

=

są małe.

Przemieszczenie liniowe nazywać będziemy

ugięciem

.

Przemieszczenie kątowe nazywać będziemy

kątem ugięcia

.

Jeżeli przyjmuje się, że

kąty ugięcia

są

bardzo małe

, to

dy

dx











2

jest jeszcze mniej-

sze. Stąd można przyjąć, że

1

1

2

3

+



























≈

dy

dx

Przy powyższych założeniach równanie (3) przyjmie postać

EI

x

Mg

dx

x

y

d

)

(

)

(

2

2

±

=

(4)

3

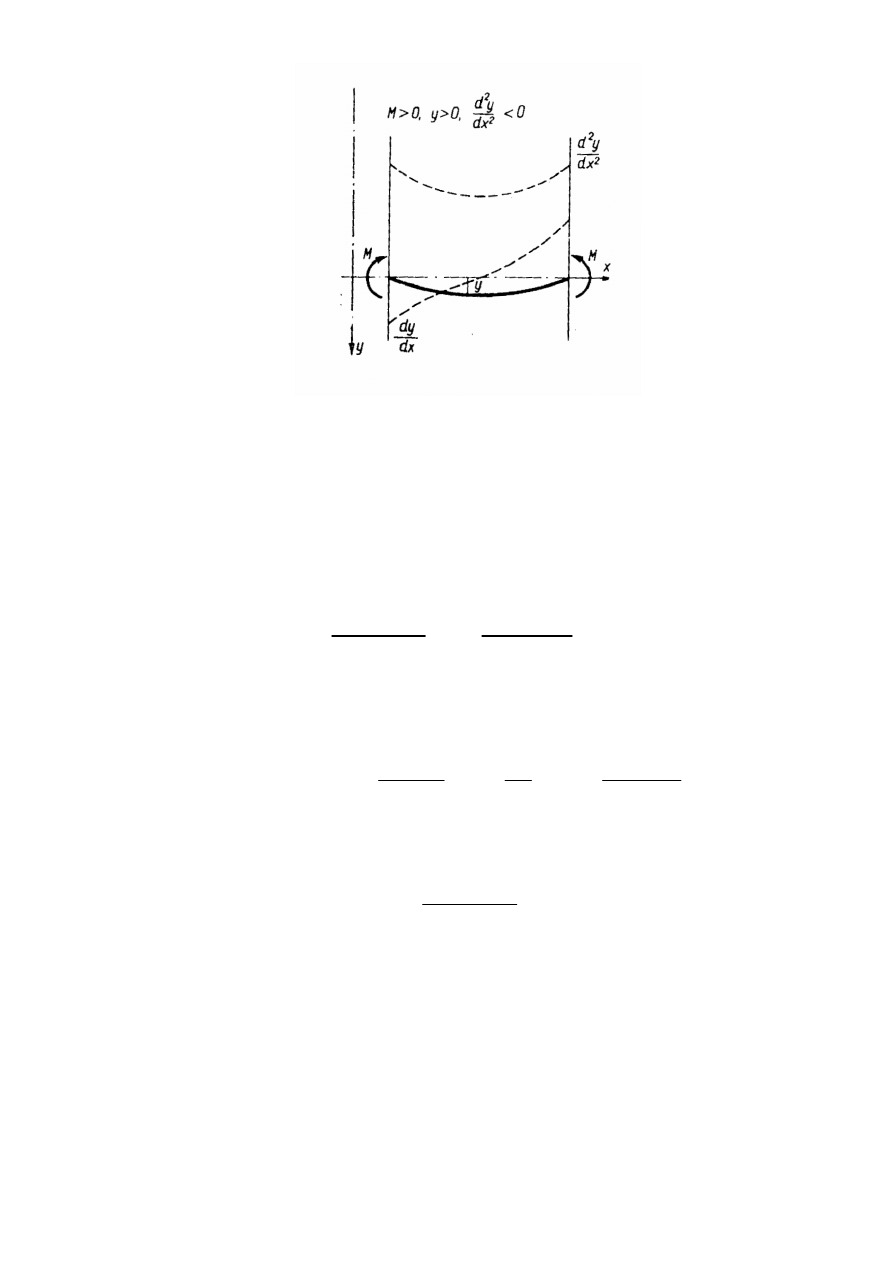
Rys.2.

Przyjęcie w równaniu (4) znaku minus lub plus zależne jest od umownego ustale-

nia znaku momentu gnącego oraz orientacji układu współrzędnych. Stosując ozna-

czenia momentu gnącego i układu osi jak na (rys.2.) równanie różniczkowe osi

ugiętej pisze się w postaci

d y x

dx

Mg x

EI

2

2

( )

( )

= −

(5)

W praktyce wymiary i materiał belki nie zmieniają się na długości pręta, w rezul-
tacie czego

EI

const

=

. Różniczkując w takim przypadku równanie (5) dwukrotnie

i uwzględniając zależność













−

=

−

=

q

dx

dT

T

dx

x

dMg

,

)

(

d Mg x

dx

q

2

2

( )

= −

otrzymuje-

my

EI

d y x

dx

q

4

4

( )

= −

(6)

W zagadnieniach inżynierskich wyznaczenie linii ugięcia belki rozpoczyna

się od określenie sił wewnętrznych T(x) i Mg(x). Następnie dwukrotnie całkując

równanie (5) otrzymujemy

4

EI

d y x

dx

Mg x

2

2

( )

( )

= −

równanie momentu

EI

dy x

dx

Mg x dx

C

( )

( )

= −

+

∫

równanie kąta ugięcia

(

)

EIy x

Mg x dx dx

Cx

D

( )

( )

= −

+

+

∫

∫

równanie linii ugięcia

Oś ugięta powinna być krzywą gładką pozbawioną załamań.

Moment gnący określa się dla danego odcinka belki równaniem analitycz-

nym. Po dwukrotnym scałkowaniu takiego równania otrzymuje się dwie stałe cał-

kowania C i D - określa się je z warunków brzegowych, to znaczy z warunków

którym muszą odpowiadać przemieszczenia na brzegach przedziałów. Warunek

ten dla punktów stanowiących granicę przedziałów wyrazi się jako warunek niero-

zerwalności

kątów ugięcia

i

przemieszczeń liniowych.

Przykład:

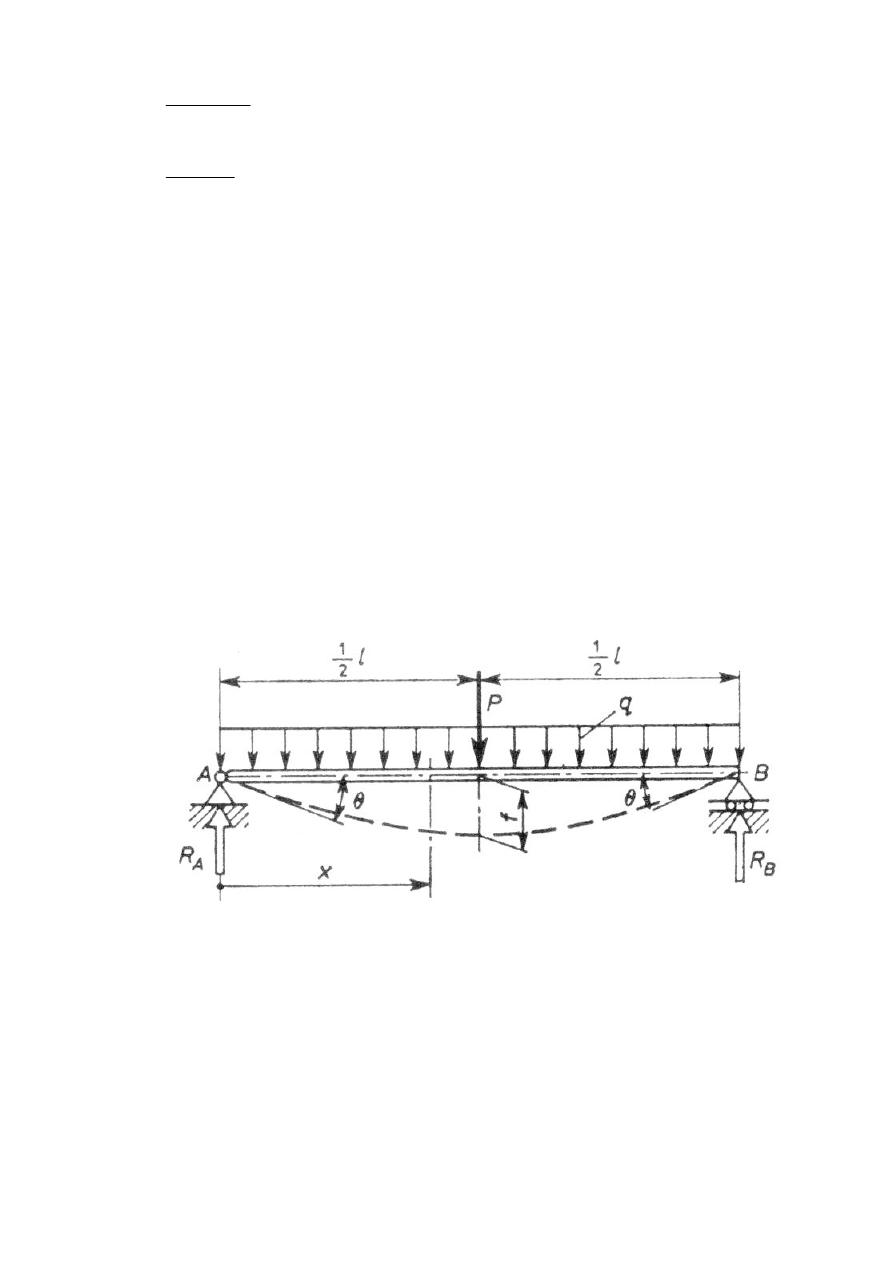
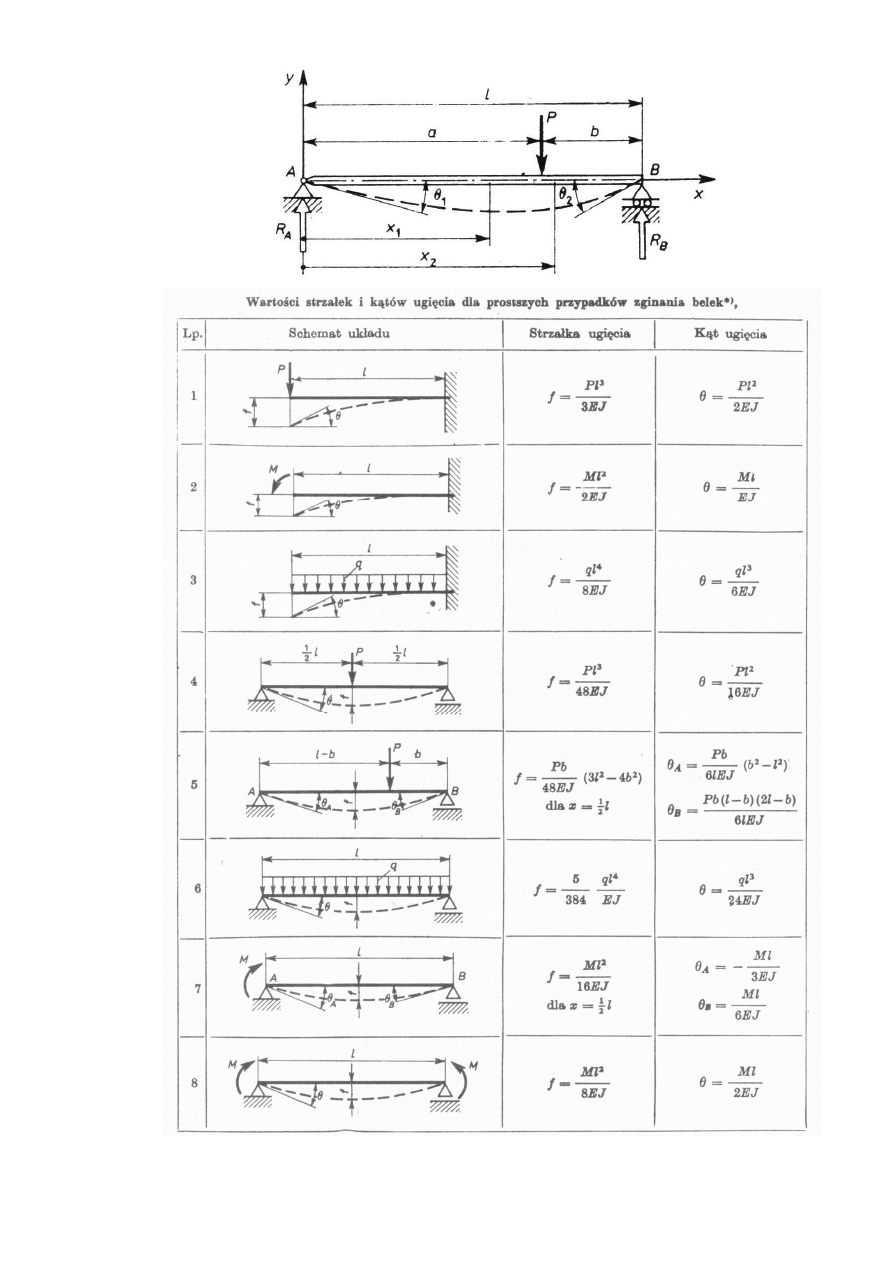
Wyznaczyć przebieg linii ugięcia belki o długości i wymiarach jak na rysunku.

Przykład:

Wyznaczyć przebieg linii ugięcia belki obciążonej siłą o długości i wymiarach jak

na rysunku.

5