LABORATORIUM MIERNICTWA
KOMPUTEROWEGO
Ćwiczenie nr 6
Pomiary ciśnień i przepływów w gazach
Użyte karty:
2 x UBR
2 x TRM1
Użyte czujniki
1. Zjawisko piezorezystancyjne w półprzewodniku.
Zjawisko piezorezystancyjne polega na zmianie oporności półprzewodnika pod
wpływem przyłożonych z zewnątrz sił powodujących odkształcenie. Jest ono
zaliczane do zjawisk kinetycznych. Odkształcenie może być opisane przy pomocy
tensora odkształceń
$
u
ik
u
u
x
u
x
u
ik
i
k
k
i
ik
=
+
⎛
⎝
⎜
⎞
⎠
⎟ =
1
2
∂
∂
∂
∂
(1.1)
który określa zmianę odległości pomiędzy punktami ciała pod wpływem
odkształcenia. Jednocześnie, przy odkształceniu w ciele powstają naprężenia
określane tensorem naprężeń
$
p
ik
Zależność pomiędzy odkształceniem, a naprężeniem określa prawo Hooke'a
p
ik
iklm
lm
l m
=
⋅ u
∑
λ
,
(1.2)
Jest to zależność liniowa, współczynnikiem proporcjonalności jest moduł sprężystości
λ (tensor 4. rzędu). Tensor λ jest symetryczny względem swych indeksów, a więc
może on posiadać 3
4
= 81 składowych, jednakże składowych o różnych wartościach
może być nie więcej, niż 21.
Kryształy półprzewodników reprezentują różne typy symetrii wynikające z układu
krystalograficznego, w którym krystalizują. Dla najczęściej spotykanych układów
krystalograficznych, liczba niezależnych modułów sprężystości - składowych tensora
modułu sprężystości - ulega zredukowaniu:
• układ trójskośny
18
• układ romboedryczny
12
• układ heksagonalny
5
1
• układ regularny
3
W spotykanych obecnie czujnikach piezorezystancyjnych materiałem wyjściowym
jest monokryształ krzemu. Krzem krystalizuje w układzie regularnym, dla którego
opis zjawisk sprężystości i piezorezystancyjnego jest wzgłędnie najprostszy.
Dla układu regularnego składowe tensora modułu sprężystości przyjęto oznaczać
jako
$
λ
λ
λ
λ
xxxx
xxyy
xyxy
oraz
λ
λ
λ
λ
λ
λ
xxxx
xxyy
xyxy
c
c
c
=
=
=
=
=
=
1111
11
1122
12
1212
44
Oddziaływanie ciśnienia zewnętrznego na kryształ półprzewodnika może przebiegać
na drodze:
• ściskania wszechstronnego,
• nacisku jednokierunkowego.
Opis zjawiska piezorezystancyjnego jest odmienny w zależności od typu
oddziaływania ciśnienia zewnętrznego. W piezorezystancyjnych czujnikach ciśnienia
wykorzystuje się z reguły zjawisko nacisku jednokierunkowego. Stąd też dalsze
rozważania ograniczymy do tego przypadku oddziaływania.
Zmiana rezystancji, powstała w wyniku zjawiska piezorezystancyjnego jest określona
zależnością
′ −
ρ
ρ
ρ
ik
ik
ik
0
0
(1.3)
gdzie
ik
ρ
ˆ i
są tensorami oporności właściwej półprzewodnika po odkształceniu i
przed odkształceniem. Wprowadzając tensor naprężeń
towarzyszący
odkształceniu uzyskać można zależność:
ik
ρ
ˆ
lm
pˆ
′ −
=
⋅
∑
ρ
ρ
ρ
ik
ik
ik
iklm
l m
lm
p
0
0
Π
,
(1.4)
gdzie
jest tensorem współczynników piezorezystancji (piezooporności). Dla
układu regularnego tensor ten ma, podobnie jak tensor modułu sprężystości, 3
składowe:
iklm
Πˆ
2
Π
Π
Π
Π
Π
Π
1111
11
1122
12
1212
44
=
=
=
Dla porównania wielkości zjawiska piezorezystancji w różnych materiałach
wprowadza się piezorezystancyjny współczynnik czułości odkształceniowej s
l
odpowiadający odkształceniu
u
wzdłuż osi l:
→
ε
ρ
ρ
ρ
l
l
u
s
Π
=
′′
−
′′
=
0
0
(1.5)
oraz
′′ = ′′ −
ρ
ρ
0
1
(
)
Π
l
p
(1.6)
gdzie:
ε - moduł Younga; p = εu - ciśnienie zewnętrzne
Π
l
- współczynnik piezorezystancji podłużnej przy przepływie prądu o
gęstości
j wzdłuż osi l;
j
E
=
′′
ρ
- piezorezystancja podłużna (wynikająca z prawa Ohma), przy braku
ciśnienia zewnętrznego (p=0)
ρ
ρ
''
''
=
0
W kryształach półprzewodnikowych współczynniki piezorezystancji
Π są
uzależnione od relacji pomiędzy kierunkiem oddziaływania ciśnienia, a kierunkiem
krystalograficznym. Dla półprzewodników krystalizujących w układzie regularnym
(german, krzem) ważna jest znajomość współczynników piezorezystancji
odpowiadających kierunkom (płaszczyznom) [100], [110], [111], dla których
składowe wektora normalnego
n
przyjmują odpowiednio
wartości
→
( , , );
,
, ;
,
,
1 0 0
1
2
1
2
0
1
3
1
3
1
3
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝⎜
⎞
⎠⎟
.
Dla kierunków tych współczynniki piezorezystancji przyjmują różne wartości:
(
)
Π
Π
Π
Π
Π
Π
Π
Π
Π
Π
Π
Π
Π
[
]
[
]
[
]
100
11
110
11
12
44
111
12
44
11
2
2
3
3
=
=
=
=
=
+
+
=
+
+
x
y
z
(1.7)
Wielkości współczynników s
l
dla kryształów półprzewodnikowych wielokrotnie
przewyższają czułość odkształceniową dla metali; np. dla krzemu typu p o oporności
ρ=0,1Ωcm,
, to jest około 60 razy więcej, niż dla typowych metali z których
wykonuje się tensometry drutowe. Ta właśnie cecha kryształów półprzewodnikowych
zadecydowała o ich atrakcyjności przy budowie elementów piezorezystancyjnych.
s
l
≅ 125
3
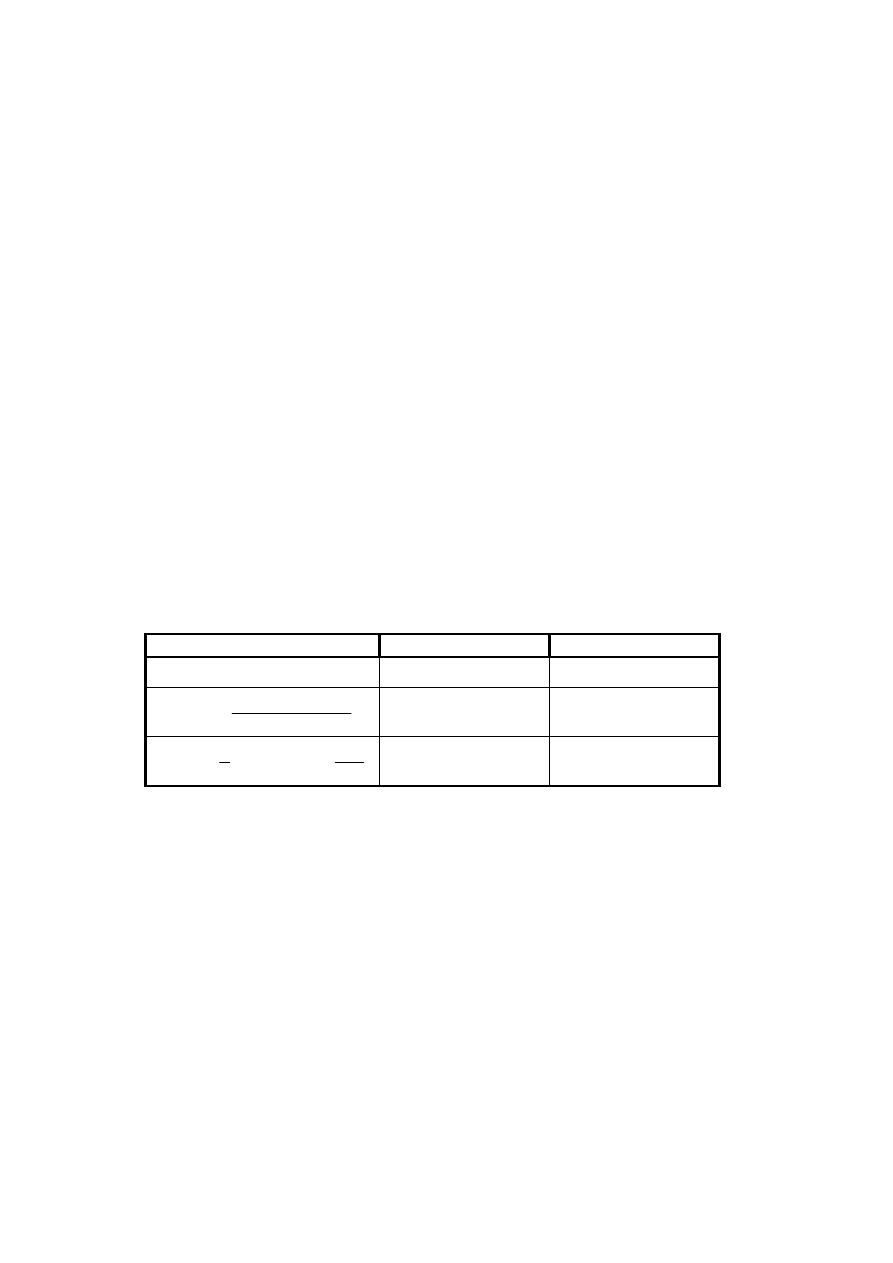
Wartości doświadczalne współczynników piezorezystancyjnych dla monokryształów
germanu i krzemu zestawiono w poniższej tabeli:
Materiał
ρ
0
Π
11
Π
12
Π
44
Π
l
=
Π
[111]
s
l[111]
[
Ω cm]
[
10
−5
cm
2
N
-1
]
Ge - n
1,5
-2,3
-3,2
-138,1
-94,9
-147
9,9
-4,7
-5,0
-137,9
-96,9
-150
Ge - p
1,1
-3,7
3,2
96,7
65,4
101,5
15,0
10,6 5,0 46,5
31,4
48,7
Si - n
7,8
6,6
-1,1
138,1
93,6
175
Si - p
11,7
-102,2
53,4
-13,6
-81,3
-142
Widoczne jest, że współczynniki te zależą od oporności właściwej oraz typu
przewodnictwa półprzewodnika. Szczegółowa interpretacja uzyskanych wyżej
wyników jest możliwa dopiero na gruncie teorii pasmowej półprzewodników.
Punktem wyjścia jest tu ogólna zależność określająca oporność właściwą
półprzewodnika:
σ
µ
ρ
=
=
−
qn
1
ˆ
(1.8)
oraz uwzględnienie typu oddziaływania zewnętrznego (ściskanie hydrostatyczne,
jednokierunkowe ściskanie lub rozciąganie) i wynikające stąd:
• zmiana szerokości pasma zabronionego:
γ
∂∆
∂
=
1
∆E
E
u
G
G
;
u - odkształcenie (1.9)
β
∂∆
∂
=
1
∆E
E
p
G
G
;
p - ciśnienie zewnętrzne (1.10)
β
γ
ε
=
;
ε - moduł Younga (1.11)
• przesunięcie poziomu Fermiego:
E
E
E
F
F
'
=
F
+ ∆
∆E
D
F
ik
i k
=
⋅ u
ik
∑
,
; (1.12)
gdzie
jest tensorem przesunięcia poziomu Fermiego, a ponadto:
ik
D
ˆ
,
(1.13)
M E
M
D
u
F
ik
i k
∆
=
⋅
=
∑
,
1
ik
gdy M jest liczbą dolin w paśmie przewodnictwa półprzewodnika.
Można wykazać, że zjawisko piezorezystancyjne przyjmuje w półprzewodnikach
znaczne wielkości (współczynniki
Π o wartościach bliskich podanym w tabeli), gdy
uwzględni się następujące fakty:
1. Powierzchnie izoenergetyczne są niesferyczne, a ruchliwość nośników jest
anizotropowa. Wówczas
)
0
(
)
ˆ
(
ˆ
σ
σ
≠
u
oraz
∆σ
∆σ
∆σ
xx
yy
zz
≠
≠
4
2. W półprzewodniku występują pasma dziur lekkich oraz ciężkich, tak że
.
A
l
h
N
p
p
=
+
Podsumowanie
W półprzewodnikach o złożonej strukturze pasmowej zjawisko
piezorezystancyjne występuje zarówno dla materiałów o przewodnictwie typu p jak i
typu n, przy czym mechanizmy dominujące w powstaniu zjawiska
piezorezystancyjnego są różne:
typ n: efekt występuje, gdy minima energii mają kształt niesferyczny i wynika ze
zmiany
rozkładu koncentracji nośników w ekstremach pasma przewodnictwa
na skutek ich przesunięcia się o wielkość
δE = f(p) dla
0
=
→
k
typ p: pod wpływem oddziaływania zewnętrznego następuje zdjęcie degeneracji
pasma walencyjnego i zmiana przewodnictwa na skutek zmiany koncentracji
dziur lekkich i ciężkich; maksima pasma walencyjnego przesuwają się o
δE k
( )
r
.
2. Krzemowe piezorezystancyjne czujniki ciśnienia
Zjawisko piezorezystancyjne znalazło zastosowanie praktyczne w budowie
piezorezystancyjnych czujników ciśnienia. W chwili obecnej w powszechnym użyciu
są czujniki krzemowe. W zależności od orientacji krystalograficznej oraz typu
przewodnictwa monokryształ krzemu wykazuje różne właściwości
piezorezystancyjne:
Współczynnik typ
p typ
n
Π
Π
[
]
100
11
=
-102,2 -6,6
Π
Π
Π
Π
[
]
110
11
12
44
2
=
+
+
-31,2 +72,3
(
)
Π
Π
Π
Π
[
]
111
12
44
11
2
3
3
=
+
+
-7,5
≈ 0
Stąd też krzemowe czujniki ciśnienia są z reguły wykonywane w materiale o
przewodnictwie typu p i orientacji krystalograficznej (100). Z takiego materiału
tworzy się w monokrysztale Si piezorezystory, przy czym najbardziej
rozpowszechnioną ich konfiguracją jest układ mostka Wheatstone’a.
Rezystory mostka są utworzone w tych miejscach struktury krzemowej, gdzie
występują maksymalne naprężenia. Zazwyczaj dwa rezystory mostka umiejscowione
są w miejscu, gdzie występuje jednokierunkowe ściskanie, zaś pozostałe dwa w
miejscu, gdzie mamy do czynienia z rozciąganiem jednokierunkowym. W takim
przypadku, pod wpływem działania ciśnienia zewnętrznego następuje maksymalne
odstrojenie mostka Wheatstone’a od stanu równowagi.
Schemat elektryczny mostkowego czujnika ciśnienia podano poniżej.
5
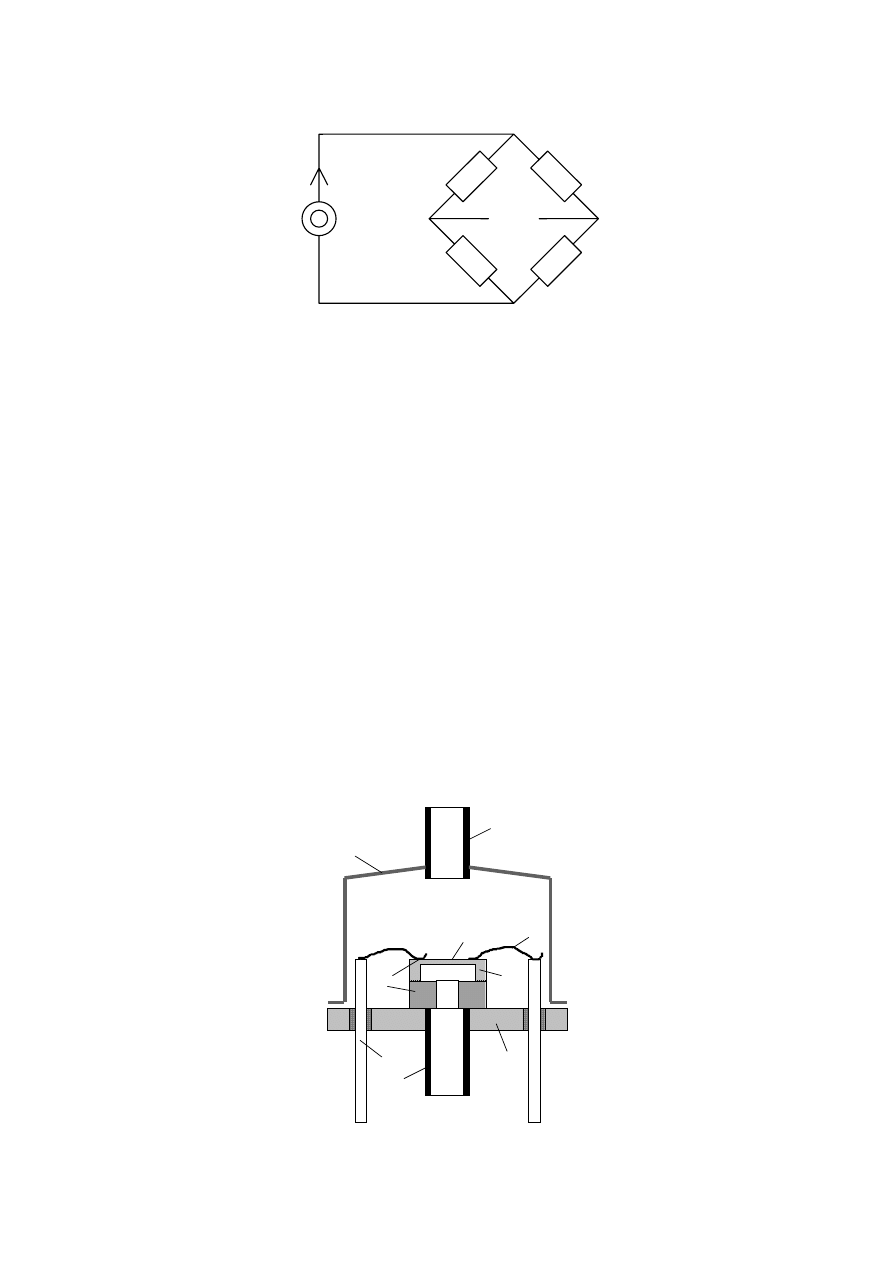
R
1
R
2
I
0
U(p)
R
3
R
4
Mostek zasilany jest prądem 1 mA z zewnętrznego źródła prądowego. Pod wpływem
ciśnienia zewnętrznego p na wyjściu czujnika pojawia się sygnał napięciowy U(p)
proporcjonalny do tego ciśnienia:
U p
I
R
kp
( )
(
)
=
+
0
0
∆
(2.1)
gdzie
∆R
0
jest tzw. niezrównoważeniem wstępnym czujnika przy braku ciśnienia
zewnętrznego (p = 0); zewnętrznie jest ono obserwowane jako napięcie U
0
, gdzie
U
I
R
0
0
0
=
⋅ ∆
(2.2)
W ćwiczeniu zastosowano krzemowe piezorezystancyjne czujniki ciśnienia typu
PS-V produkowane przez “VIGOTOR” Sp. z o.o. w Toruniu. Schemat czujnika
przedstawiono na poniższym schemacie:
Schemat budowy czujnika ciśnienia typu PS-V, produkowanego
przez VIGOTOR Sp. z o. o. w Toruniu
8
9
1a 4
2 1
3
5 6
7
6
Oznaczenia na rysunku:
1.
struktura
krzemowa
1a.
obszar
ciśnienioczuły (membrana)
2.
piezorezystor
3.
podłoże szklane
4.
wyprowadzenie
drutowe
5.
wyprowadzenie
obudowy
6.
podstawa
obudowy
7.
doprowadzenie
ciśnienia lub podciśnienia mierzonego
8.
doprowadzenie
nadciśnienia mierzonego lub ciśnienia odniesienia
9.
osłona obudowy.
7
3. Pomiary ciśnień i przepływów w gazach i cieczach.
Czujniki piezorezystancyjne są stosowane do pomiarów ciśnień w płynach (cieczach i
gazach). Ciśnienia mogą być mierzone stacjonarnie w takim punkcie instalacji
ciśnieniowej, w której zamontowany jest czujnik ciśnienia. Sygnał napięciowy z
czujnika, proporcjonalny do ciśnienia, może być następnie odpowiednio przetwarzany
przez odpowiednie układy wykonawcze.
Zamontowanie czujników ciśnienia w minimum dwóch miejscach instalacji
ciśnieniowej umożliwia określenie przepływu płynu w instalacji na podstawie
rejestracji dwóch różnych wartości ciśnienia.
Objętość cieczy lub gazu przepływająca w jednostce czasu przez powierzchnię
przekroju rury jest dana zależnością:
Q
A v
= ⋅
(3.1)
gdzie A jest powierzchnią przekroju a v średnią prędkością przepływu przez przekrój.
Powyższa zależność jest słuszna dla przepływu laminarnego.
Prędkość przepływu płynu może być wyznaczona różnymi sposobami, najprostszym
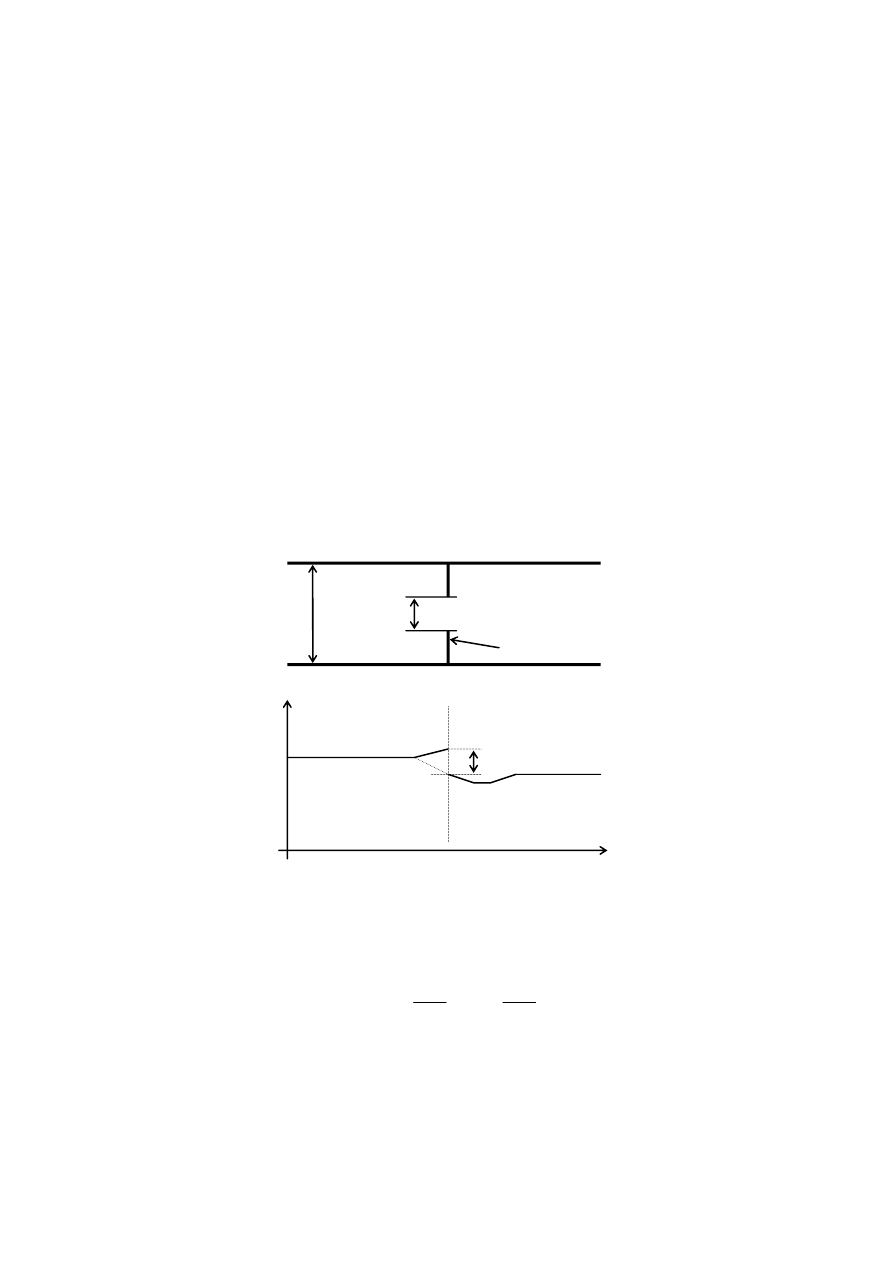
jest model t. zw. przepływomierza zwężkowego z kryzą.
rura
D d
zwężka
p
p
1
∆p p
2
x
Rys. 3.1
Rozkład ciśnień przy przepływie przez zwężkę pokazany jest jakościowo na rysunku
3.1. Prędkość przepływu wyznaczyć można na podstawie równania Bernoulliego:
p
V
p
V
1
1
2
2
2
2
2
2
+
=
+
ρ
ρ
(3.2)
gdzie
ρ jest gęstością płynu, oraz zakładając ciągłość przepływu:
v A
v A
1 1
2
2
=
(3.3)
Na podstawie powyższych równań prędkość przepływu można wyznaczyć z
zależności:
8
v
p
p
A
A
1
1
2
1
2
2
2
2
1
=
−
−
⎛
⎝
⎜
⎞
⎠
⎟
(
)
ρ
(3.4)
Wyraża ona prędkość przepływu płynu w przewodzie rurowym. Natomiast strumień
łynu przepływającego przez przewód (przepływ) w czasie
∆t można określić jako:
p
Q
A v
t
=
1 1
∆
(3.5)
Pomiar przepływu może być zrealizowany w opa
rzewodzie o zmiennej średnicy. Najczęściej stosowane są kalibrowane przewężenia
rciu o pomiary różnicy ciśnień w
p
występujące jako tzw. kryzy, dysze oraz zwężki Venturiego. W najprostszym
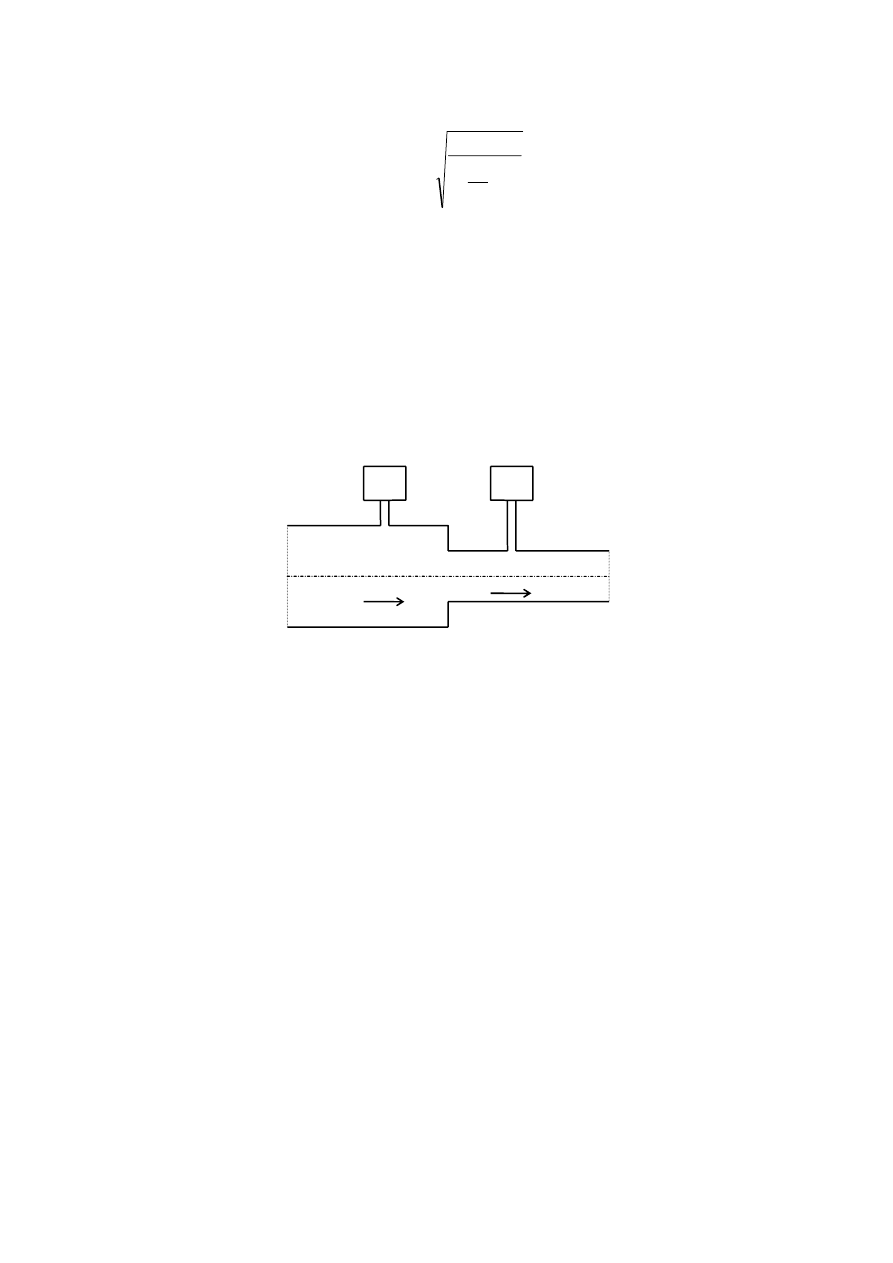
przypadku wykonuje się układ pomiarowy, jak na rysunku:
S
1
S
2
A
1
p
1
p
2
A
2
v
1
v
2
Składa się on z dwóch odcinków rur o przekrojach A
1
i A
2
. W warunkach
dynamicznego przepływu w części szerszej panuje ciśnienie p
1
, za płyn przepływa z
e z obszarem
ępują przy
ś
prędkością v
1
. Odpowiednio dla części węższej o przekroju A
2
parametry przepływu
wynoszą odpowiednio p
2
i v
2
. Ciśnienia p
1
i p
2
są mierzone przez czujniki S
1
i S
2
;
wielkość przepływu może zostać wyznaczona ze wzorów (3.4) i (3.5).
Przy dokładniejszych pomiarach przepływu pamiętać należy o zaburzeniach
związanych z tarciem i zawirowaniami płynu związanymi główni
zmiany kształtu przewodu. Rzeczywiste przewężenie strumienia zaczyna się nieco
przed kryzą osiągając minimum nieco za nią. Przed i za kryzą tworzy się strefa ruchu
wirowego. Początkowe ciśnienie strumienia przy ściance przewodu wzrasta nieco
przed kryzą, zmniejszając się za nią i osiągając minimum na wysokości największego
przewężenia strumienia. Na dalszym odcinku przewodu strumień rozszerza się, a jego
ciśnienie przy ściance wzrasta do wartości nieco mniejszej od początkowej. Różnica
ciśnień spowodowana zakłóceniem toru przepływu wynosi
∆p.
Niniejsza strata ciśnienia spowodowana jest głównie przez straty energii płynu na
skutek tarcia oraz tworzenia się wirów. Największe straty ciśnienia wyst
zwężeniach kryzowych, mniejsze w przypadku dysz, najmniejsze w przypadku
zwężek Venturiego. Również wielkość zwężenia (d
2
/d
1
) wpływa na wielkość
zakłóceń przepływu; w optymalnym z punktu widzenia pomiarowego, przypadku
(d
2
/d
1
= 0,6) straty ciśnienia na zwężce Venturiego wynoszą kilka procent. Pamiętać
jednak należy, aby punkty pomiarów ciśnień czujnikami S
1
i S
2
były dostatecznie
9
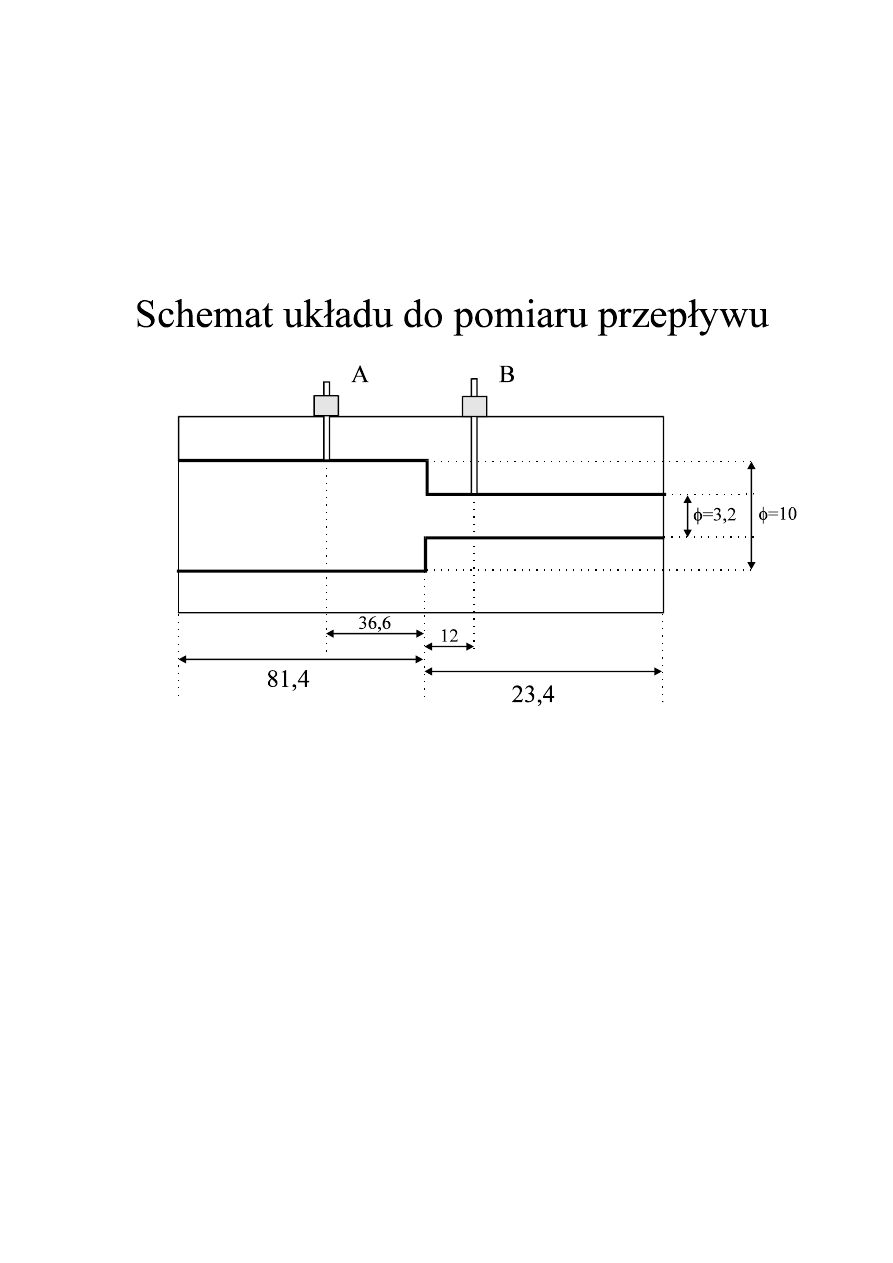
oddalone (l >= 3d) od punktu zmiany średnicy przewodu. Czujniki rejestrować
wówczas będą ciśnienia p
1
oraz p
2
nie zakłócone przez zmianę kształtu przewodu.
10