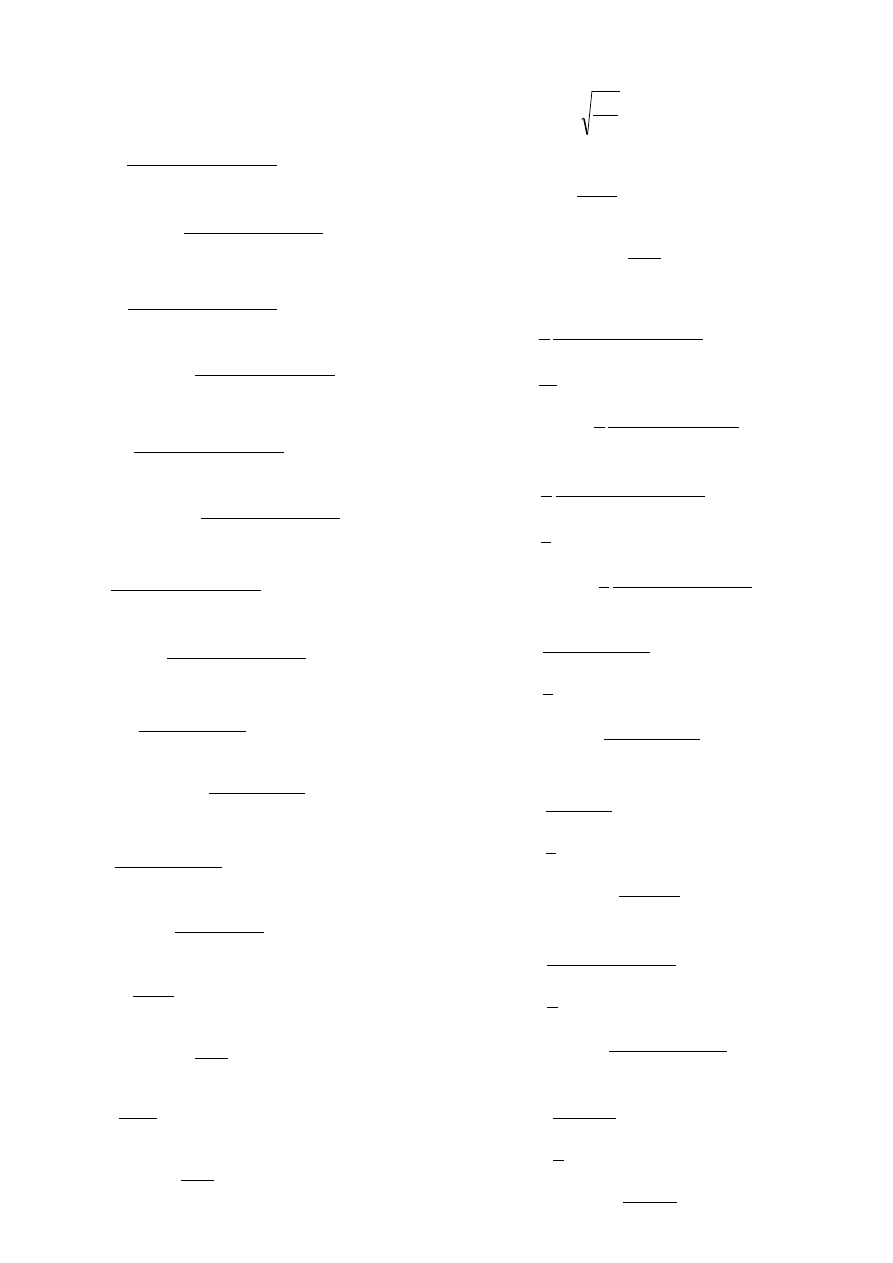
Funkcje występujące we wzorach transformacyjnych zginania
z udziałem dużych sił osiowych

î

í

ě

<

>

=

0

S

gdy

~

0

S

gdy

|

|

s

s

EJ

S

l

ď

ď

î

ď

ď

í

ě

=

+

-

+

-

=

=

>

-

-

-

=

.

~

dla

~

~

)

~

1

(

2

~

~

~

)

~

(

~

0,

dla

4

0,

dla

sin

)

cos

1

(

2

cos

sin

)

(

s

s

s

s

s

s

s

s

s

s

a

s

s

s

s

s

s

s

s

s

s

a

i

sh

ch

ch

sh

ď

ď

î

ď

ď

í

ě

=

+

-

-

-

=

=

>

-

-

-

=

.

~

dla

~

~

)

~

1

(

2

~

~

~

)

~

(

~

0,

dla

2

0,

dla

sin

)

cos

1

(

2

sin

)

(

s

s

s

s

s

s

s

s

s

b

s

s

s

s

s

s

s

s

s

b

i

sh

ch

sh

ď

ď

î

ď

ď

í

ě

=

+

-

-

-

=

=

>

-

-

-

=

.

~

dla

~

~

)

~

1

(

2

)

~

1

(

~

)

~

(

~

0,

dla

6

0,

dla

sin

)

cos

1

(

2

)

cos

1

(

)

(

2

2

s

s

s

s

s

s

s

s

J

s

s

s

s

s

s

s

s

J

i

sh

ch

ch

ď

ď

ď

î

ď

ď

ď

í

ě

=

+

-

+

-

=

=

>

-

-

-

=

.

~

dla

)

~

1

(

~

~

)

~

1

(

2

2

1

)

~

(

~

0,

dla

12

1

0,

dla

)

cos

1

(

sin

)

cos

1

(

2

2

1

)

(

2

2

s

s

s

s

s

s

s

s

g

s

s

s

s

s

s

s

s

g

i

ch

sh

ch

ď

ď

î

ď

ď

í

ě

=

-

-

=

˘

=

>

-

=

˘

.

~

dla

~

~

~

~

~

)

~

(

~

0,

dla

3

0,

dla

cos

sin

sin

)

(

2

2

s

s

s

s

s

s

s

s

a

s

s

s

s

s

s

s

s

a

i

ch

sh

sh

ď

ď

ď

î

ď

ď

ď

í

ě

=

+

-

+

-

=

˘

=

>

-

-

-

=

˘

.

~

dla

)

~

~

~

(

~

~

~

)

~

1

(

2

2

1

)

~

(

~

0,

dla

8

1

0,

dla

)

cos

(sin

sin

)

cos

1

(

2

2

1

)

(

s

s

s

s

s

s

s

s

s

s

g

s

s

s

s

s

s

s

s

s

s

g

i

ch

sh

sh

ch

ď

ď

î

ď

ď

í

ě

=

=

˘

˘

=

>

=

˘

˘

.

~

dla

~

~

~

)

~

(

0,

dla

1

0,

dla

sin

cos

)

(

s

s

s

s

s

s

a

s

s

s

s

s

s

a

i

sh

ch

ď

ď

î

ď

ď

í

ě

=

=

˘

˘

=

>

=

˘

˘

.

~

dla

~

~

)

~

(

~

0,

dla

1

0,

dla

sin

)

(

s

s

s

s

s

b

s

s

s

s

s

b

i

sh

ď

ď

ď

î

ď

ď

ď

í

ě

=

-

=

=

>

-

=

˘

˘

.

~

dla

~

~

~

~

~

)

~

(

~

0,

dla

3

1

0,

dla

sin

cos

sin

)

(

2

''

2

s

s

s

s

s

s

s

s

g

s

s

s

s

s

s

s

s

g

i

sh

sh

ch

i

i

ď

ď

ď

î

ď

ď

ď

í

ě

=

-

-

=

=

>

-

=

˘

˘

.

~

dla

~

~

~

~

)

~

(

~

0,

dla

6

1

0,

dla

sin

sin

)

(

2

''

2

s

s

s

s

s

s

s

g

s

s

s

s

s

s

s

g

i

sh

sh

k

k

ď

ď

î

ď

ď

í

ě

=

=

˘

˘

˘

=

>

-

=

˘

˘

˘

.

~

dla

~

~

~

)

~

(

~

0,

dla

0

0,

dla

cos

sin

)

(

s

s

s

s

s

s

a

s

s

s

s

s

s

a

i

ch

sh

ď

ď

ď

î

ď

ď

ď

í

ě

=

-

+

=

˘

˘

˘

=

>

+

-

=

˘

˘

˘

.

~

dla

~

~

~

1

~

~

)

~

(

~

0,

dla

2

1

0,

dla

cos

cos

1

sin

)

(

2

2

s

s

s

s

s

s

s

s

g

s

s

s

s

s

s

s

s

g

i

ch

ch

sh

ď

ď

î

ď

ď

í

ě

=

+

-

=

=

>

-

-

=

.

~

dla

~

~

)

~

1

(

2

~

~

)

~

(

~

0,

dla

12

0,

dla

sin

)

cos

1

(

2

sin

)

(

3

3

s

s

s

s

s

s

s

s

d

s

s

s

s

s

s

s

s

d

i

sh

ch

sh

ď

ď

î

ď

ď

í

ě

=

-

=

˘

=

>

-

=

˘

.

~

dla

~

~

~

~

~

)

~

(

~

0,

dla

3

0,

dla

cos

sin

cos

)

(

3

3

s

s

s

s

s

s

s

s

d

s

s

s

s

s

s

s

s

d

i

ch

sh

ch

ď

ď

ď

î

ď

ď

ď

í

ě

=

-

=

=

>

-

=

.

~

dla

~

~

1

~

)

~

(

~

0,

dla

2

1

0,

dla

cos

cos

1

)

(

2

2

s

s

s

s

s

s

g

s

s

s

s

s

s

g

i

ch

ch

IV

IV