Funkcja homograficzna, definicje i wykres
1. Definicja:
Funkcja homograficzna to funkcja wymierna, będąca ilorazem dwóch funkcji liniowych:
![]()
2. Wyróżnikiem funkcji homograficznej nazywamy liczbę:
Δ a⋅b - b⋅c
3. Założenia dotyczące liczb a, b, c, d.
a) a, b, c, d ∈ R
b) c ≠ 0
Jeśli c=0 to mianownik jest liczbą stałą, a więc f(x) jest wtedy funkcją liniową, a nie homograficzną.
c) Δ ≠ 0
Jeśli Δ to licznik i mianownik zawierają tę samą funkcję liniową, zatem ich iloraz równa się 1. Otrzymujemy wówczas funkcję stałą.
d) d ≠ -c
Gdy d = c, mianownik jest zerem, a więc wyrażenie f(x) traci sens matematyczny
4. Dziedzina i zbiór wartości:
![]()
![]()
5. Postać kanoniczna:
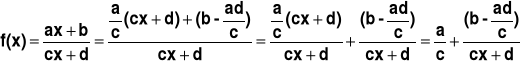
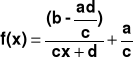
6. Punkty przecięcia z osiami (o ile istnieją):
![]()
(gdy b=0, punkt nie należy do dziedziny)
![]()
7. Wykresem każdej funkcji homograficznej (o ile spełnia ona założenia z punktu 3.) jest hiperbola:
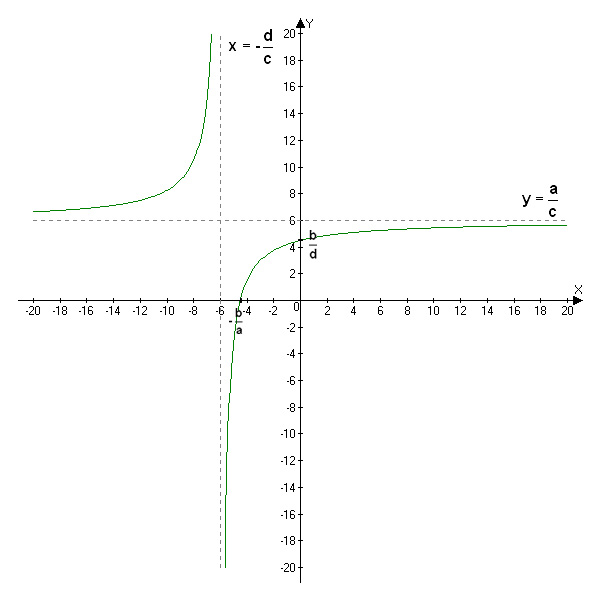
8. Monotoniczność:
Δ > funkcja rosnąca
Δ funkcja malejąca
(Δ - patrz: punkt 2)
9. Przykład:
Szczególnym przypadkiem funkcji homograficznej jest:
![]()
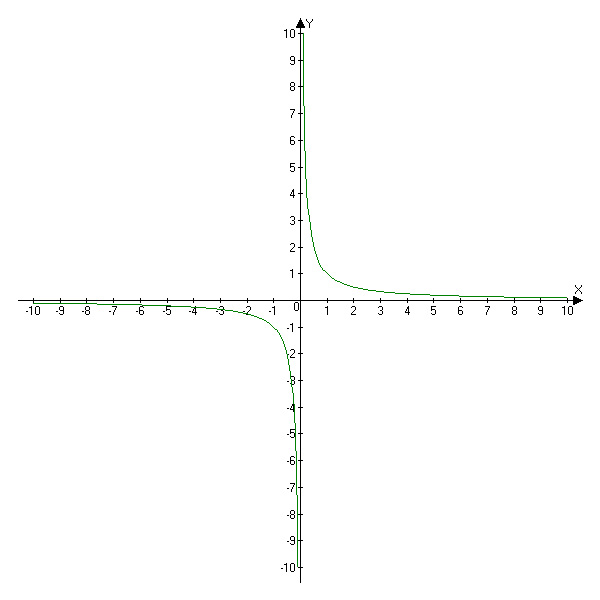
10. Sposób rysowania wykresów:
sprowadzamy funkcję do postaci kanonicznej (pkt. 5)
rysujemy wykres funkcji
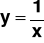
rozszerzamy/zwężamy wykres z punktu b
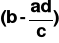
razy w pionierozszerzamy/zwężamy wykres z punktu c c razy w poziomie
przesuwamy wykres z punktu d o wektor:
![]()
(lub układ o wektor przeciwny)
Przykład:
![]()
a) ![]()
b) patrz: punkt 9
c) rozszerzamy wykres 3-krotnie w pionie
d) pozostawiamy wykres nietknięty (c = 1)
e) przesuwamy wykres o wektor:
![]()
lub układ o:
![]()
© Marcin Kordasz, IVa
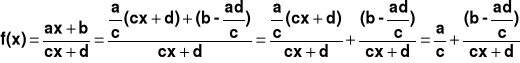
Wyszukiwarka
Podobne podstrony:
tm30-Układ równań, Funkcja homograficzna, definicje i wykres
Zróżnicowanie funkcjonalne języka polskiego - wykres, Nauka o komunikowaniu, Kultura języka
Jak realizuje się funkcja poetycka definicja figury poetyckiej
Funkcjonariusz publiczny definicja
makroekonomia wzory definicje wykresy uek sum ujecie keynesowskie
[Audi A4 TDI, TURBO] Zasady działania turbo, schemat, definicje, wykres
Funkcja homograficzna
FUNKCJA HOMOGRAFICZNA, Matematyka
przeksztalcenie funkcji homograficznej, Matematyka, Liceum
Funkcja homograficzna, Matematyka, Matematyka(4)
Zestaw 1 Funkcja kwadratowa Funkcja homograficzna Równanie liniowe
gim Wykresy funkcji - gimnazjum, gimnazjum i podstawówka, gimnazjum, polak, matma
Definicja całki nieoznaczonej i funkcji pierwotnej
Matematyka cw8 Badanie funkci Wykres funkcji
controlling - definicja i funkcje, zarzadzanie
WŁASNOŚCI FUNKCJI ODCZYTYWANE Z WYKRESU
Wykresy funkcji (2)
Przekształcenia wykresów funkcji
więcej podobnych podstron