Rozwiązywanie równań
różniczkowych

Wersja robocza

Metody numeryczne i statystyka

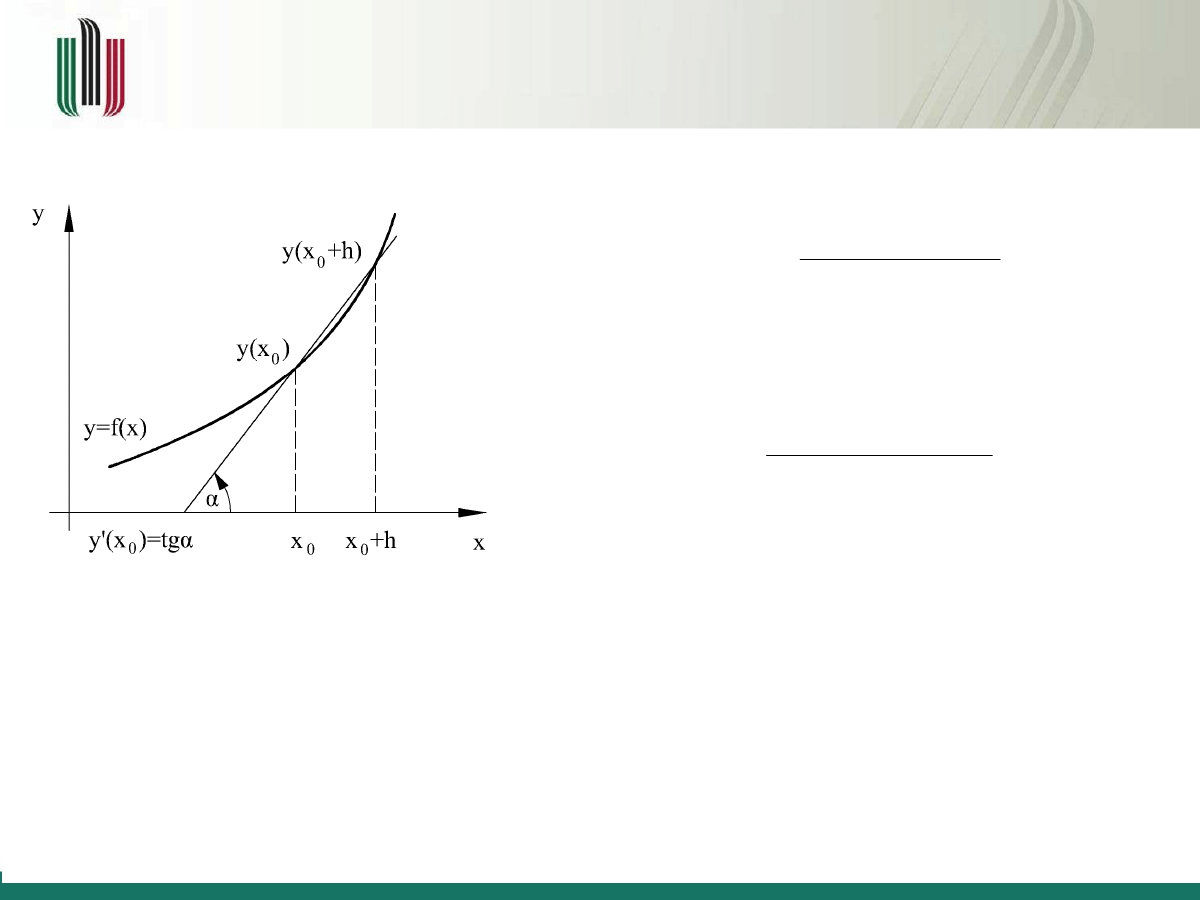
Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

2

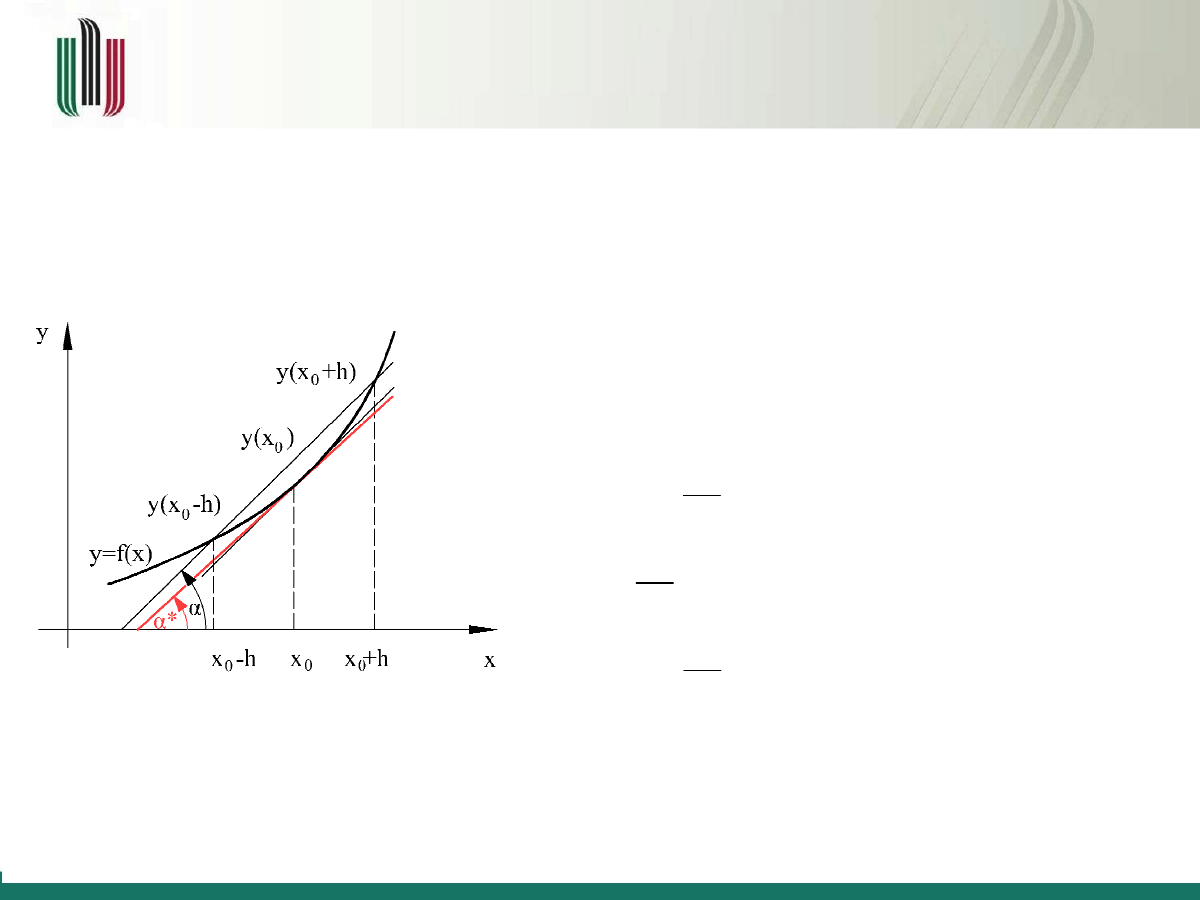
Różniczkowanie numeryczne – metoda

różniczkowania jednopunktowego w przód

Pierwsza pochodna funkcji f (x) zdefiniowana jest jako

h

x

y

h

x

y

x

y

)

(

)

(

)

(

'

0

0

0

−

+

≈

h

x

f

h

x

f

x

f

h

)

(

)

(

lim

)

(

'

0

−

+

=

→

Zagadnienie to można rozwiązać numerycznie poprzez
proste przybliżenie przy ustalonej wielkości kroku

h

Chcemy obliczyć pochodną funkcji

f (x).

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

3

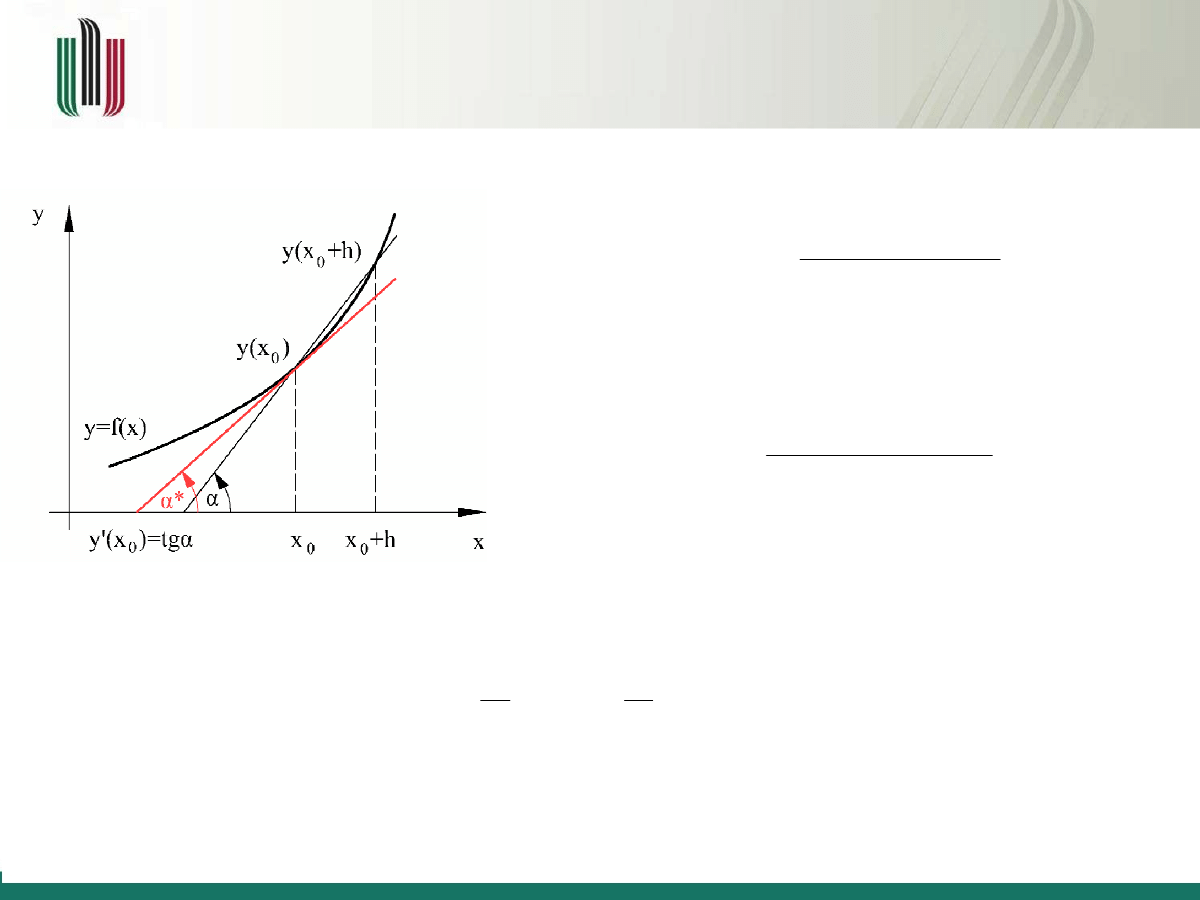
Różniczkowanie numeryczne – metoda

różniczkowania jednopunktowego w przód

Pierwsza pochodna funkcji f (x) zdefiniowana jest jako

h

x

y

h

x

y

x

y

)

(

)

(

)

(

'

0

0

0

−

+

≈

h

x

f

h

x

f

x

f

h

)

(

)

(

lim

)

(

'

0

−

+

=

→

Zagadnienie to można rozwiązać numerycznie poprzez
proste przybliżenie przy ustalonej wielkości kroku

h

W celu analizy popełnianego błędu wyrażenie

y (x

0

+ h)

można rozwinąć w szereg Taylora

w zależności od

x

0

Chcemy obliczyć pochodną funkcji

f (x).

(

)

( )

( )

...

)

(

''

'

!

3

)

(

''

!

2

'

0

3

0

2

0

0

0

+

⋅

+

⋅

+

⋅

+

=

+

x

y

h

x

y

h

x

y

h

x

y

h

x

y

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

4

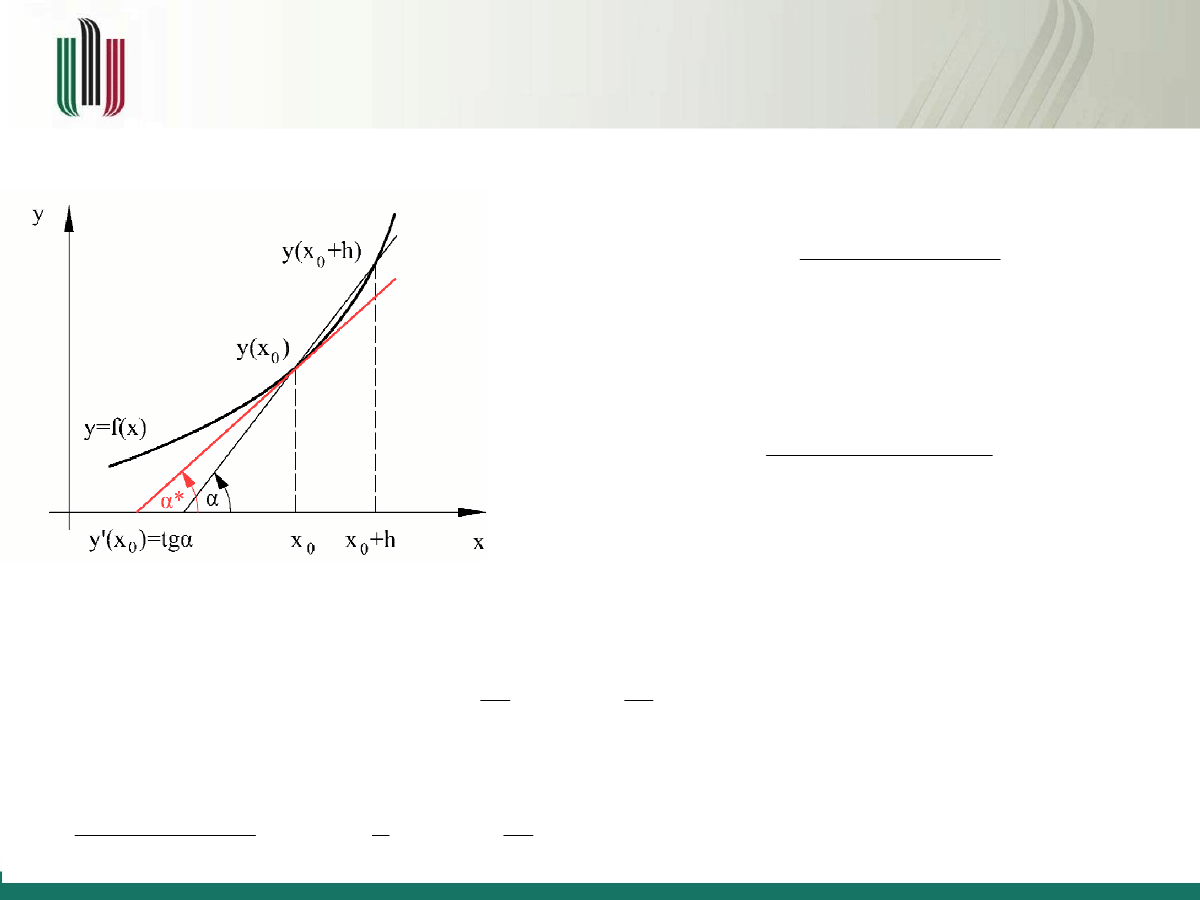
Różniczkowanie numeryczne – metoda

różniczkowania jednopunktowego w przód

Pierwsza pochodna funkcji f (x) zdefiniowana jest jako

h

x

y

h

x

y

x

y

)

(

)

(

)

(

'

0

0

0

−

+

≈

h

x

f

h

x

f

x

f

h

)

(

)

(

lim

)

(

'

0

−

+

=

→

Zagadnienie to można rozwiązać numerycznie poprzez
proste przybliżenie przy ustalonej wielkości kroku

h

W celu analizy popełnianego błędu wyrażenie

y (x

0

+ h)

można rozwinąć w szereg Taylora

w zależności od

x

0

Po odjęciu od obu stron

y (x

0

)

i podzieleniu obu stron przez

h

otrzymujemy

Chcemy obliczyć pochodną funkcji

f (x).

(

)

( )

( )

...

)

(

''

'

!

3

)

(

''

!

2

'

0

3

0

2

0

0

0

+

⋅

+

⋅

+

⋅

+

=

+

x

y

h

x

y

h

x

y

h

x

y

h

x

y

(

) ( )

( )

...

)

(

''

'

!

3

)

(

''

2

'

0

2

0

0

0

0

+

⋅

+

⋅

+

=

−

+

x

y

h

x

y

h

x

y

h

x

y

h

x

y

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

5

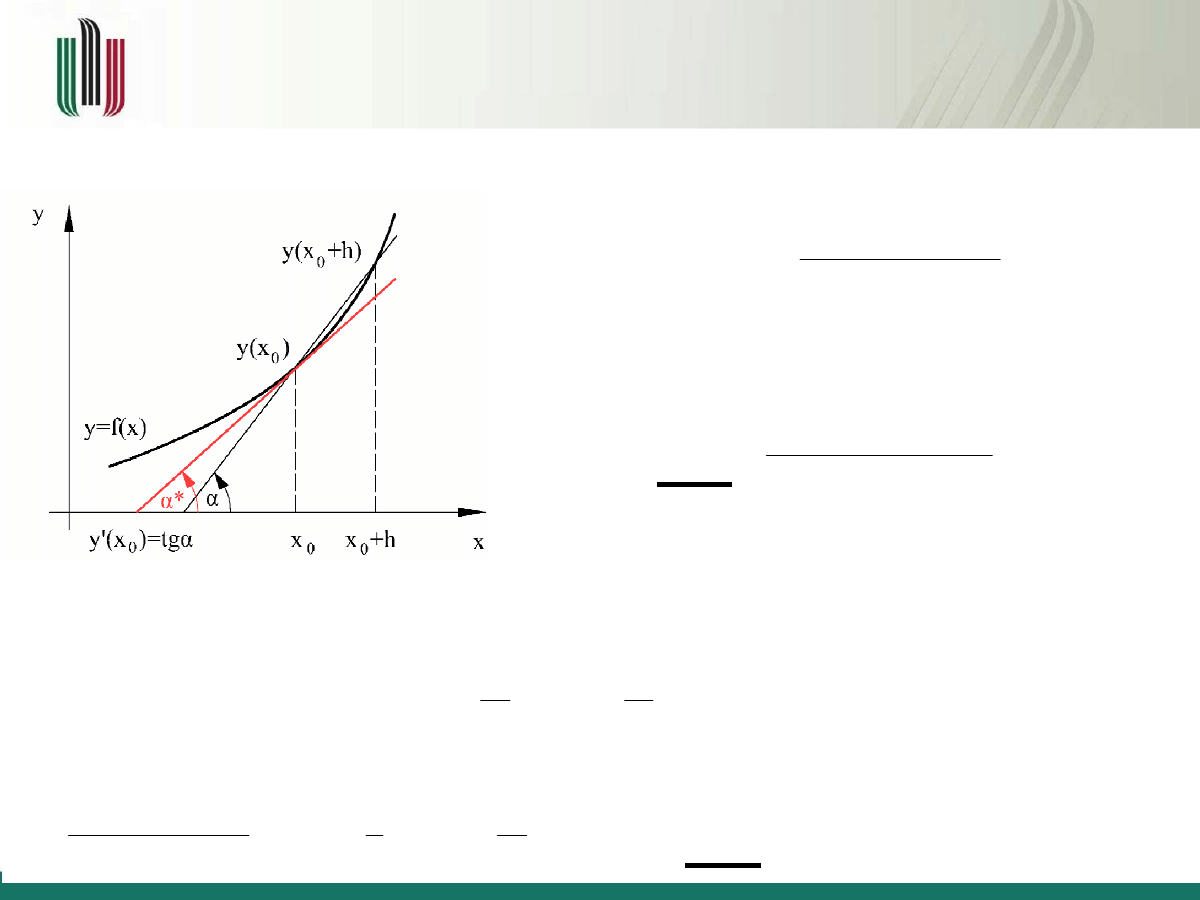
Różniczkowanie numeryczne – metoda

różniczkowania jednopunktowego w przód

Pierwsza pochodna funkcji f (x) zdefiniowana jest jako

h

x

y

h

x

y

x

y

)

(

)

(

)

(

'

0

0

0

−

+

≈

h

x

f

h

x

f

x

f

h

)

(

)

(

lim

)

(

'

0

−

+

=

→

Zagadnienie to można rozwiązać numerycznie poprzez
proste przybliżenie przy ustalonej wielkości kroku

h

W celu analizy popełnianego błędu wyrażenie

y (x

0

+ h)

można rozwinąć w szereg Taylora

w zależności od

x

0

Po odjęciu od obu stron

y (x

0

)

i podzieleniu obu stron przez

h

otrzymujemy

, gdzie O(h) – błąd obcięcia

Chcemy obliczyć pochodną funkcji

f (x).

(

)

( )

( )

...

)

(

''

'

!

3

)

(

''

!

2

'

0

3

0

2

0

0

0

+

⋅

+

⋅

+

⋅

+

=

+

x

y

h

x

y

h

x

y

h

x

y

h

x

y

(

) ( )

( )

( )

)

(

'

...

)

(

''

'

!

3

)

(

''

2

'

0

0

2

0

0

0

0

h

O

x

y

x

y

h

x

y

h

x

y

h

x

y

h

x

y

+

=

+

⋅

+

⋅

+

=

−

+

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

6

Różniczkowanie numeryczne – metoda

różniczkowania trójpunktowego

Przybliżone wartości pochodnej funkcji można także obliczyć posługując się algorytmem
różniczkowania trójpunktowego. Można z niego skorzystać gdy wartości zmiennej

niezależnej podawane są ze stałym krokiem

h

i znane są wartości zmiennej zależnej

)

(

),

(

),

(

0

0

0

h

x

y

x

y

h

x

y

+

−

Wartość pochodnych określa się w przybliżeniu jako

[

]

[

]

[

]

)

(

3

)

(

4

)

(

2

1

)

(

'

)

(

)

(

2

1

)

(

'

)

(

)

(

4

)

(

3

2

1

)

(

'

0

0

0

0

0

0

0

0

0

0

0

h

x

y

x

y

h

x

y

h

h

x

y

h

x

y

h

x

y

h

x

y

h

x

y

x

y

h

x

y

h

h

x

y

+

+

−

−

=

+

+

+

−

−

=

+

−

+

−

−

=

−

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

7

Różniczkowanie numeryczne – metoda

różniczkowania trójpunktowego

[

]

[

]

[

]

n

n

n

n

i

i

i

y

y

y

h

y

n

i

y

y

h

y

y

y

y

h

y

3

4

2

1

1

,...,

3

,

2

,

2

1

4

3

2

1

1

2

'

1

1

'

3

2

1

'

1

+

−

=

−

=

+

−

=

−

+

−

=

−

−

+

−

- pierwszy punkt

- pozostałe punkty

- ostatni punkt

W praktyce korzysta się ze wzorów zapisanych iteracyjnie:

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

8

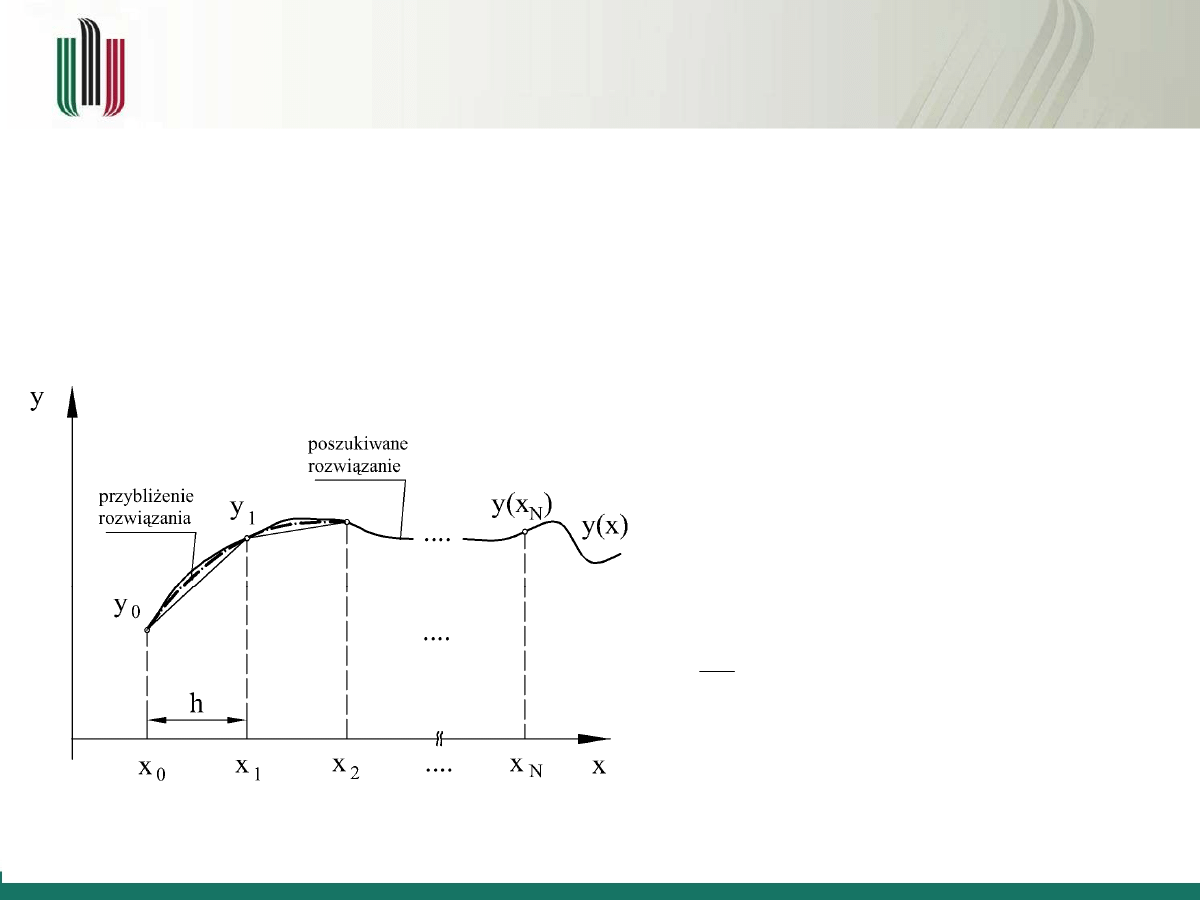
Rozwiązywanie równań różniczkowych

– metoda Eulera

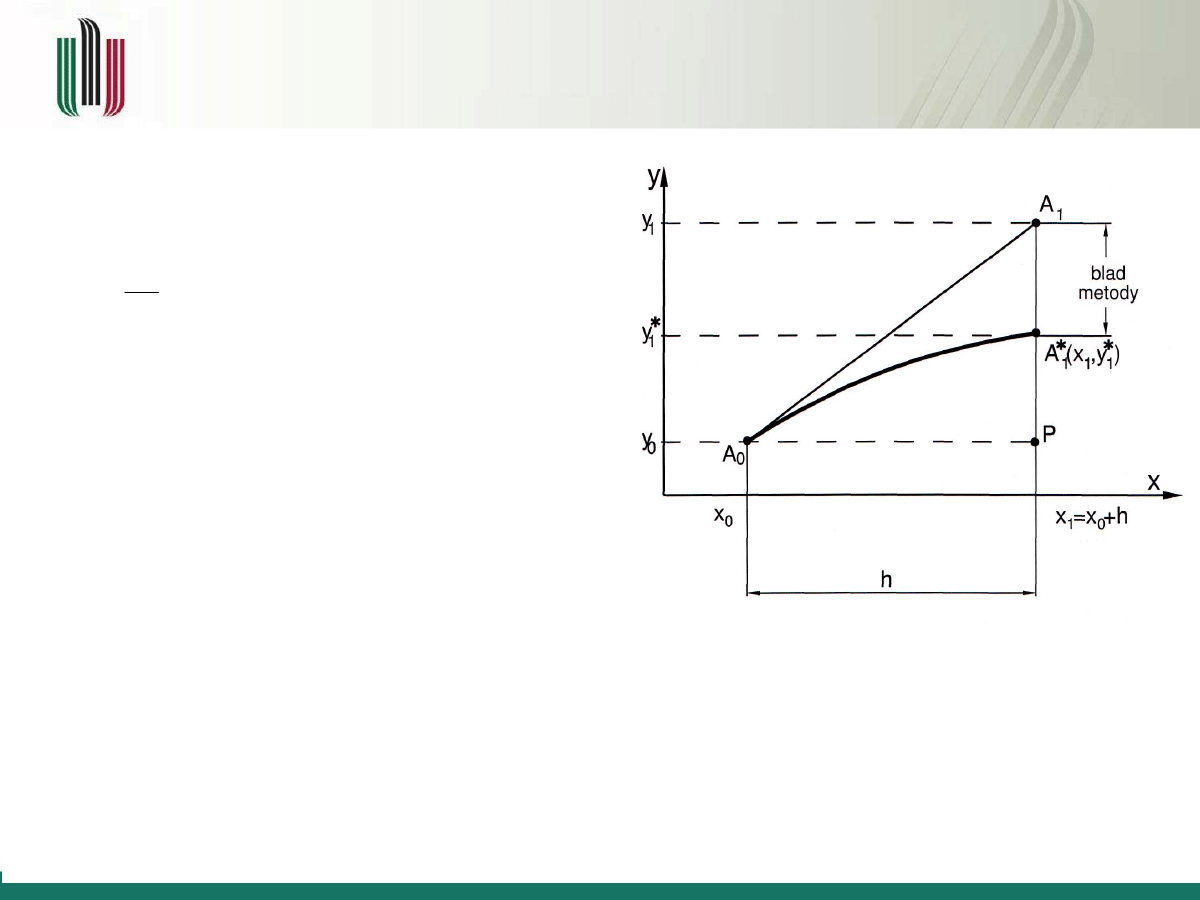
Poszukiwane jest rozwiązanie
równania różniczkowego postaci:

z warunkiem początkowym

Rozwiązaniem omawianego problemu
jest poszukiwana wartość funkcji

w

Przyjmijmy, że

y* = y (x

1

)

i krzywa

(A

0

A

1

*)

są rozwiązaniem zadania. Znając punkt

A

0

(x

0

, y

0

)

(warunek początkowy) można obliczyć wartość funkcji

f

w tym punkcie. Jest to współczynnik

kierunkowy stycznej do

y (x)

w punkcie

x

0

.

Następnie wyznaczany jest punkt przecięcia tej

stycznej z prostą

x = x

1

i oznaczany przez

A

1

(x

1

, y

1

).

Takie postępowanie prowadzi do

powstania błędu metody przy wyznaczaniu wartości

y

i

(

)

[

]

b

x

x

x

y

x

f

dx

dy

,

,

)

(

,

0

∈

=

0

0

)

(

y

x

y

=

)

(x

y

y =

h

x

x

x

+

=

=

0

1

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

9

Rozwiązywanie równań różniczkowych

– metoda Eulera

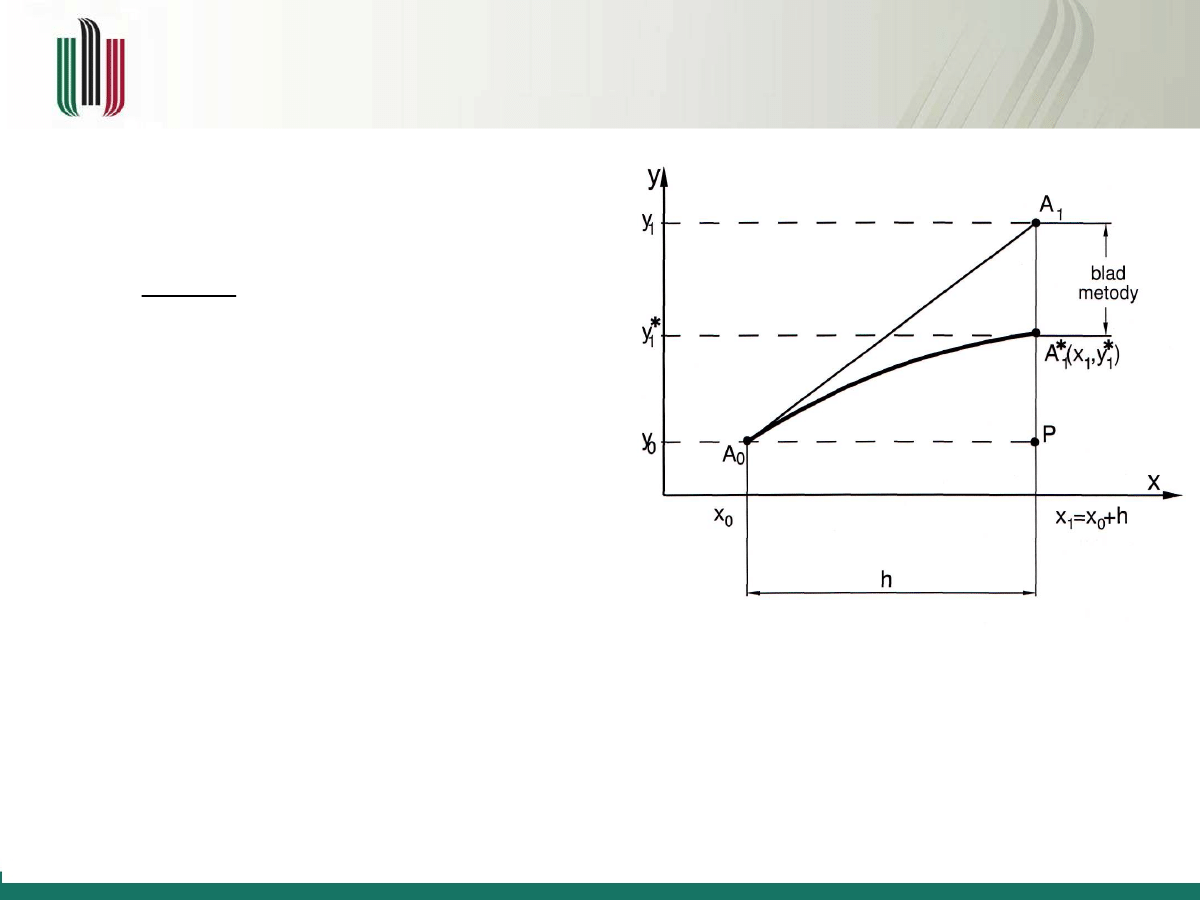
Spróbujmy sformalizować sposób obliczania

y

i

w postaci wzoru. Z trójkąta (

A

0

A

1

P)

mamy:

stąd

Chcąc wyznaczyć wartość funkcji

y

2

w punkcie

x

2

= x

1

+ h = x

0

+ 2 h

postępujemy analogicznie, tylko zamiast
korzystać z warunku początkowego korzystamy

z uprzednio obliczonych wartości

(x

1

, y

1

).

Uogólniając takie postępowanie można zapisać:

gdzie

y

i

jest wartością funkcji stanowiącej rozwiązanie równania różniczkowego w

x

i

(

)

0

0

0

1

, y

x

f

h

y

y

=

−

(

)

0

0

0

1

, y

x

f

h

y

y

⋅

+

=

(

)

,...

2

,

1

,

,

1

1

1

=

⋅

+

=

−

−

−

i

y

x

f

h

y

y

i

i

i

i

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

10

Metoda Eulera

Metodę Eulera można otrzymać w inny sposób. Zastępując funkcję

y = y (x)

w

x = x

0

+ h

jej rozwinięciem w szereg Taylora otrzymujemy:

Wykorzystując dwa pierwsze wyrazy rozwinięcia w szereg Taylora:

co można inaczej napisać:

Podany wzór jest identyczny jak uzyskany uprzednio. Powtarzając takie postępowanie jak

w poprzednim wyprowadzeniu wzór ten można uogólnić

(

)

( )

( )

...

)

(

''

!

2

'

0

2

0

0

0

+

⋅

+

⋅

+

=

+

x

y

h

x

y

h

x

y

h

x

y

(

)

( )

( )

0

0

0

' x

y

h

x

y

h

x

y

⋅

+

≅

+

(

)

0

0

0

1

, y

x

f

h

y

y

⋅

+

=

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

12

Metoda Rungego-Kutty rzędu II

Przypuśćmy, że znamy

y (x

i -1

)

i chcemy wyznaczyć przybliżenie

y

i

wartości

y (x

i -1

+ h)

. Idea

metod Rungego-Kutty polega na obliczeniu wartości

f (x, y)

w pewnych szczególnie

dobranych punktach leżących w pobliżu krzywej rozwiązania w przedziale

(x

i -1

, x

i -1

+ h)

oraz

utworzeniu takiej kombinacji tych wartości, która z dobrą dokładnością daje przyrost

y

i

– y

i -1

(

)

0

0

)

(

,

)

(

,

y

x

y

x

y

x

f

dx

dy

=

=

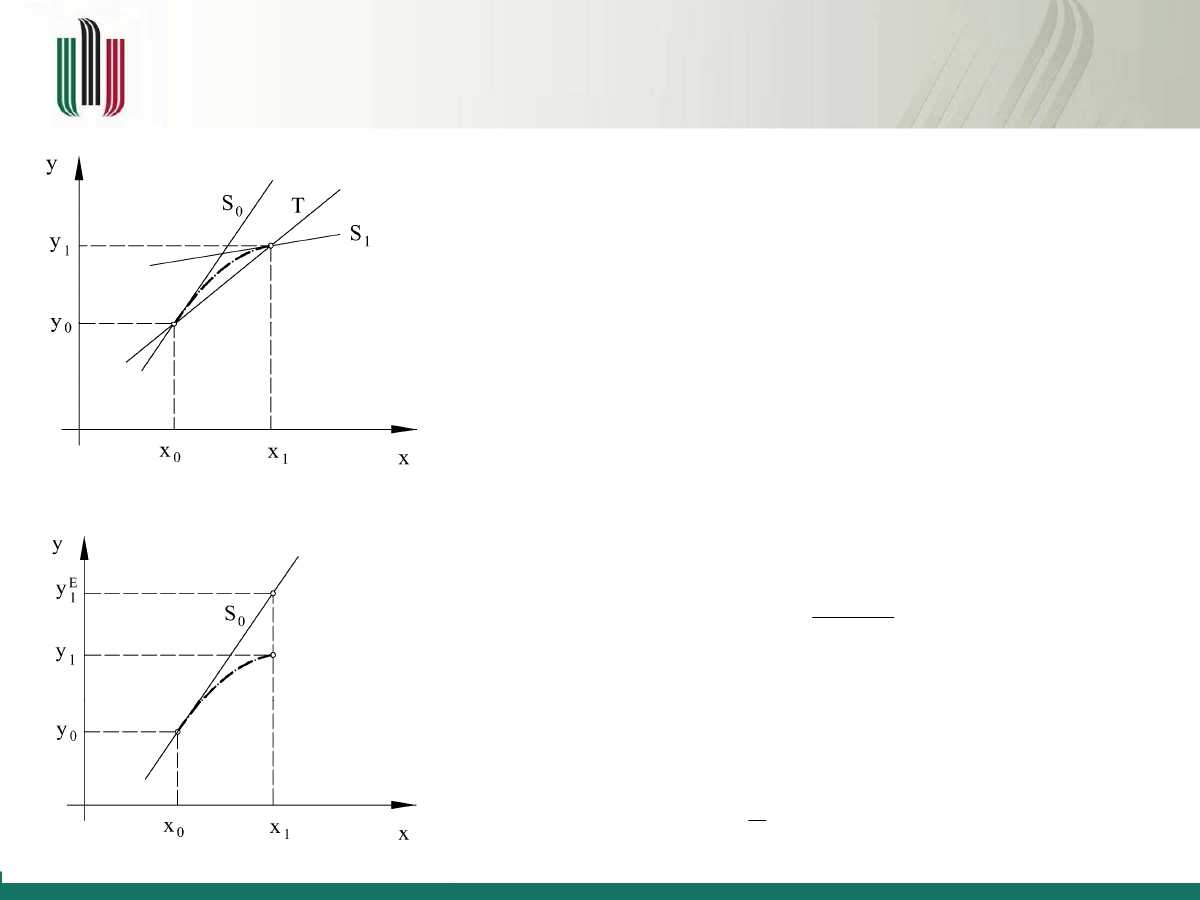
Rozważmy metodę Rungego-Kutty II
rzędu, opartą na przybliżeniu rozwiązania
równania różniczkowego za pomocą
krzywej opisanej wielomianem stopnia II
(parabolą).

Równanie różniczkowe ma postać

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

13

Metoda Rungego-Kutty rzędu II

Korzystając z własności paraboli, dla której współczynnik kierunkowy
siecznej T równy średniej arytmetycznej współczynników
kierunkowych stycznych i w punktach o współrzędnych odpowiednio

(x

0

, y

0

), (x

1

, y

1

)

.

Pozwala to na przybliżenie rozwiązania równania różniczkowego
łamaną utworzoną z siecznych, a nie stycznych jak miało to miejsce
w metodzie Eulera.

Ponieważ nie jest znana postać rozwiązania rzędną

y

1

przybliża się

wartością wyznaczoną z metody Eulera

Można zapisać przybliżenie poszukiwanego rozwiązania w punkcie

o współrzędnych

(x

1

, y

1

)

w sposób następujący

Podstawiając za współczynnik kierunkowy stycznej

S

0

wyrażenie

f (x

0

, y

0

)

oraz za współczynnik kierunkowy stycznej

S

1

wyrażenie

f (x

1

, )

otrzymuje się

E

y

1













+

+

=

2

1

0

0

1

S

S

h

y

y

E

y

1

(

)

(

)

[

]

E

y

x

f

y

x

f

h

y

y

1

1

0

0

0

1

,

,

2

1

+

+

=

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

14

Metoda Rungego-Kutty rzędu II

Pamiętając o tym, że:

wyrażenie na

y

1

można zapisać następująco

)

,

(

0

0

1

0

1

y

x

hf

y

h

x

x

E

=

+

=

oraz

(

)

(

)

(

)

[

]

0

0

0

0

0

0

0

1

,

,

,

2

1

y

x

f

h

y

h

x

f

h

y

x

f

h

y

y

⋅

+

+

⋅

+

⋅

+

=

Oznaczając

(

)

[

]

1

0

0

1

0

1

,

2

1

k

y

h

x

f

h

k

y

y

+

+

⋅

+

+

=

)

,

(

0

0

1

y

x

hf

k =

Wyrażenie przyjmuje postać

Zastępując wyrażenie współczynnikiem

k

2

otrzymuje się wzór na

metodę Rungego-Kutty II w postaci

(

)

1

0

0

,

k

y

h

x

f

h

+

+

⋅

[

]

(

)

(

)

1

0

0

2

0

0

1

2

1

0

1

,

,

2

1

k

y

h

x

hf

k

y

x

hf

k

k

k

y

y

+

+

=

=

+

+

=

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

15

Metoda Rungego-Kutty rzędu II

Wyznaczając kolejne wartości poszukujemy funkcji

y

i

stanowiącej przybliżone rozwiązanie

równania różniczkowego w oparciu o sieczne według przedstawionej metodyki wzór metody
Rungego-Kutty II przyjmuje ogólną postać:

[

]

(

)

(

)

N

i

k

y

h

x

hf

k

y

x

hf

k

k

k

y

y

i

i

i

i

i

i

,...,

2

,

1

1

1

1

2

1

1

1

2

1

1

,

,

2

1

=

+

+

=

=

+

+

=

−

−

−

−

−

dla

(

)

(

)

(

)

...

,

,

,

2

1

1

1

3

1

1

1

2

1

1

1

k

k

y

bh

x

hf

k

k

y

ah

x

hf

k

y

x

hf

k

i

i

i

i

i

i

γ

β

α

+

+

+

=

+

+

=

=

−

−

−

−

−

−

Ogólnie metody Rungego-Kutty polegają na takim dobraniu współczynników

a, b, …, α, β, γ

,…

oraz liczb

R

1

,

R

2

,… tak aby wartość

y

i

określona przez ciąg równań była możliwie jak najbliższa

dokładnej wartości:

,...

2

,

1

...,

2

,

1

,

...

2

2

1

1

1

=

=

+

+

+

+

=

−

n

i

k

R

k

R

k

R

y

y

n

n

i

i

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

16

Metoda Rungego-Kutty rzędu IV

gdzie

Najbardziej znana jest metoda Rungego-Kutty czwartego rzędu opisana zależnością

(

)

4

3

2

1

1

2

2

6

1

k

k

k

k

y

y

i

i

+

⋅

+

⋅

+

+

=

−

)

,

(

)

2

,

2

(

)

2

,

2

(

)

,

(

3

1

1

4

2

1

1

3

1

1

1

2

1

1

1

k

y

h

x

f

h

k

k

y

h

x

f

h

k

k

y

h

x

f

h

k

y

x

f

h

k

i

i

i

i

i

i

i

i

+

+

⋅

=

+

+

⋅

=

+

+

⋅

=

⋅

=

−

−

−

−

−

−

−

−

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

17

Rozwiązywanie równań różniczkowych

pierwszego rzędu

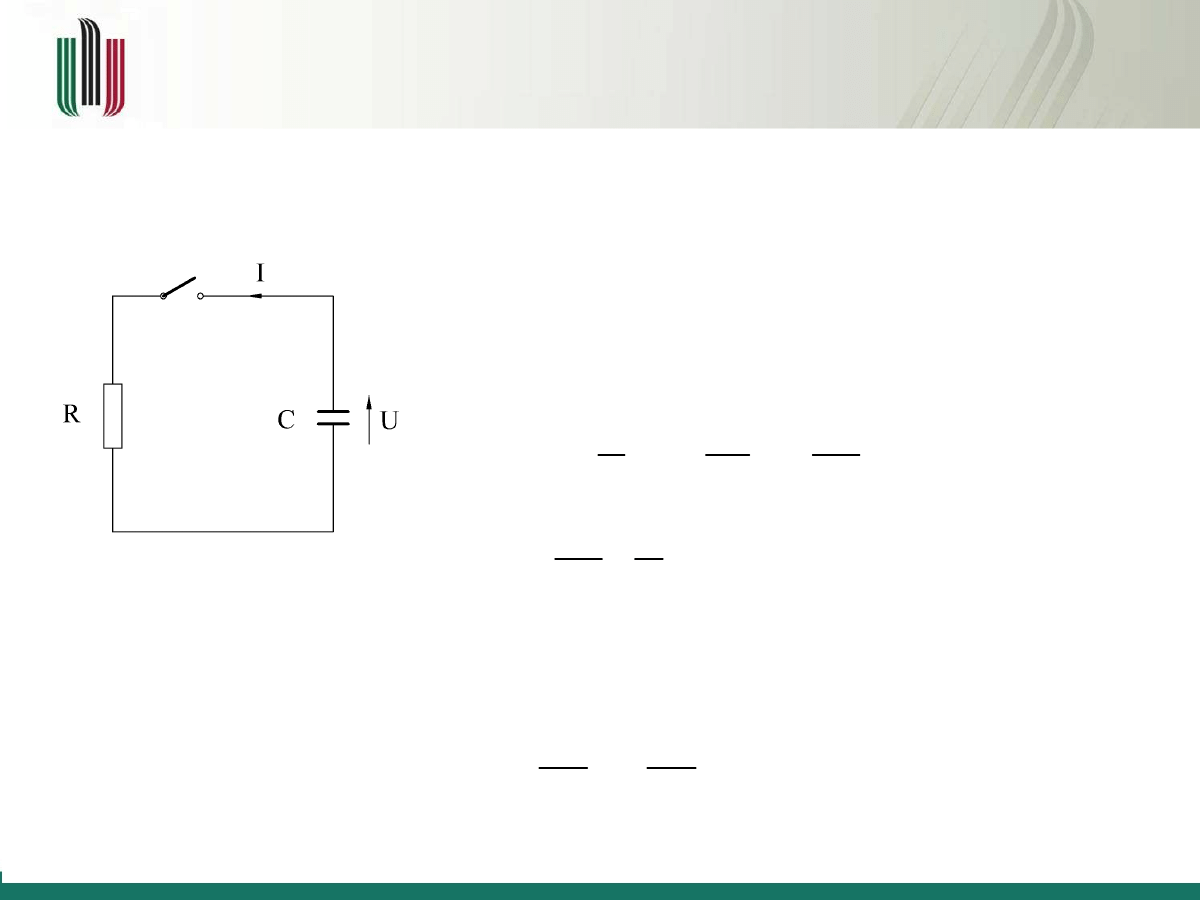
Rozpatrzmy obwód elektryczny w którym kondensator

o pojemności

C

został naładowany do napięcia

U =U

0

.

W chwili

t = 0

został zwarty włącznik

W

i nastąpiło

rozładowanie kondensatora przez oporność

R

Jest to równanie różniczkowe zwyczajne rzędu I . Aby je rozwiązać dzielimy obie

strony równania przez

C

oraz po lewej stronie pozostawiamy najwyższą pochodną

U

Przykład 1 - Rozładowanie kondensatora przez opornik

dt

dU

C

dt

dQ

I

C

Q

U

=

=

=

,

, Q

- ładunek

0

=

+

R

U

dt

dU

C

RC

U

dt

dU

−

=

W

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

18

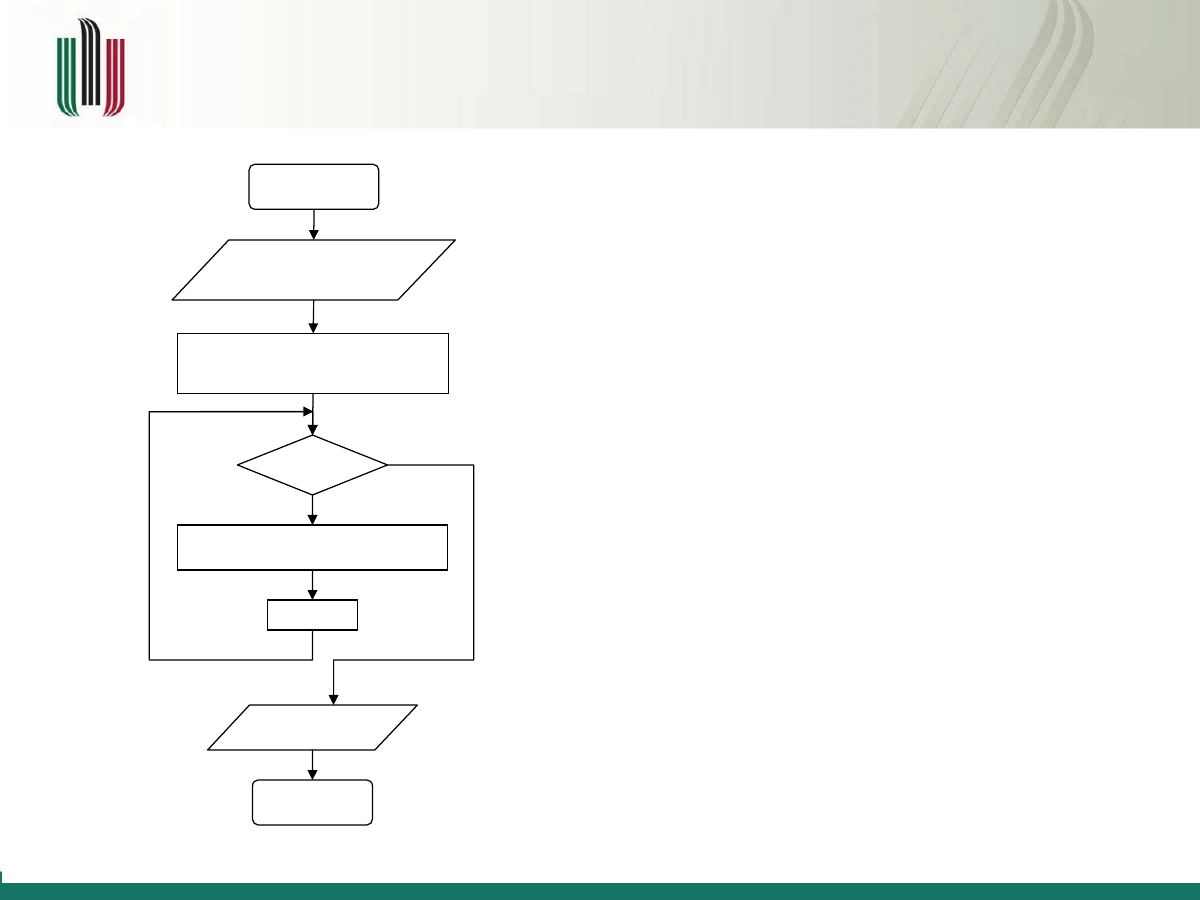
Algorytm metody Eulera

Etap:

1.

Zdefiniowanie funkcji

f (x, y (x))

, przyjęcie granic

badanego przedziału

[x

0

, x

k

]

, liczby kroków

N

, wartości

początkowej

y

0

2.

Obliczenie długości kroku

h

, dyskretyzacja przedziału

[x

0

, x

k

]

3.

Pętla obliczająca rekurencyjnie

i

-te wartości

y

i

na

podstawie wzoru Eulera

4.

Wynik – dyskretna funkcja

y (x

i

)

będąca przybliżeniem

rozwiązania równania różniczkowego

(

)

N

i

y

x

f

h

y

y

i

i

i

i

,...,

2

,

1

,

,

1

1

1

=

⋅

+

=

−

−

−

Start

f (x, y (x)),

x

0

, x

k

, N, y

0

h = (x

k

- x

0

) / N

x

i

=h·i, i=1,2,...,N

i≤N

Koniec

y(x

i

)

tak

y

i+1

=y

i

+h·f(x

i

,y(x

i

))

i=i+1

nie

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

19

Rozwiązywanie równań różniczkowych

pierwszego rzędu

Rozwiązanie metodą Eulera dla danych: napięcie początkowe

U

0

= 10

[V] w chwili

t

0

=

0

[s],

oporność

R = 10

[Ω], pojemność

C = 0,1

[F], czas końcowy

t

k

= 2

[s], ilość kroków

N = 4

Dla równania różniczkowego o postaci

Wzór iteracyjny Eulera ma postać:

(

)

N

i

y

x

f

h

y

y

i

i

i

i

,...,

2

,

1

,

,

1

1

1

=

⋅

+

=

−

−

−

(

)

[

]

k

x

x

x

x

y

x

f

dx

dy

,

,

)

(

,

0

∈

=

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

20

Rozwiązywanie równań różniczkowych

pierwszego rzędu

Rozwiązanie metodą Eulera dla danych: napięcie początkowe

U

0

= 10

[V] w chwili

t

0

=

0

[s],

oporność

R = 10

[Ω], pojemność

C = 0,1

[F], czas końcowy

t

k

= 2

[s], ilość kroków

N = 4

Dla równania różniczkowego o postaci

Wzór iteracyjny Eulera ma postać:

Za funkcję

można podstawić:

W przedziale

[x

0

,x

k

]

rozwiązanie jest badane dla wartości

x

i

= x

i-1

+ h, gdzie x

0

= 0, x

k

= 2,

h = 0,5

Wartość początkowa

y

0

= U

0

= 10

(

)

N

i

y

x

f

h

y

y

i

i

i

i

,...,

2

,

1

,

,

1

1

1

=

⋅

+

=

−

−

−

(

)

[

]

k

x

x

x

x

y

x

f

dx

dy

,

,

)

(

,

0

∈

=

(

)

)

(

,

x

y

x

f

(

)

)

(

)

(

,

x

y

a

x

y

x

f

⋅

=

, gdzie

)

(

)

(

,

1

1

t

U

x

y

RC

a

=

−

=

−

=

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

21

Rozwiązywanie równań różniczkowych

pierwszego rzędu

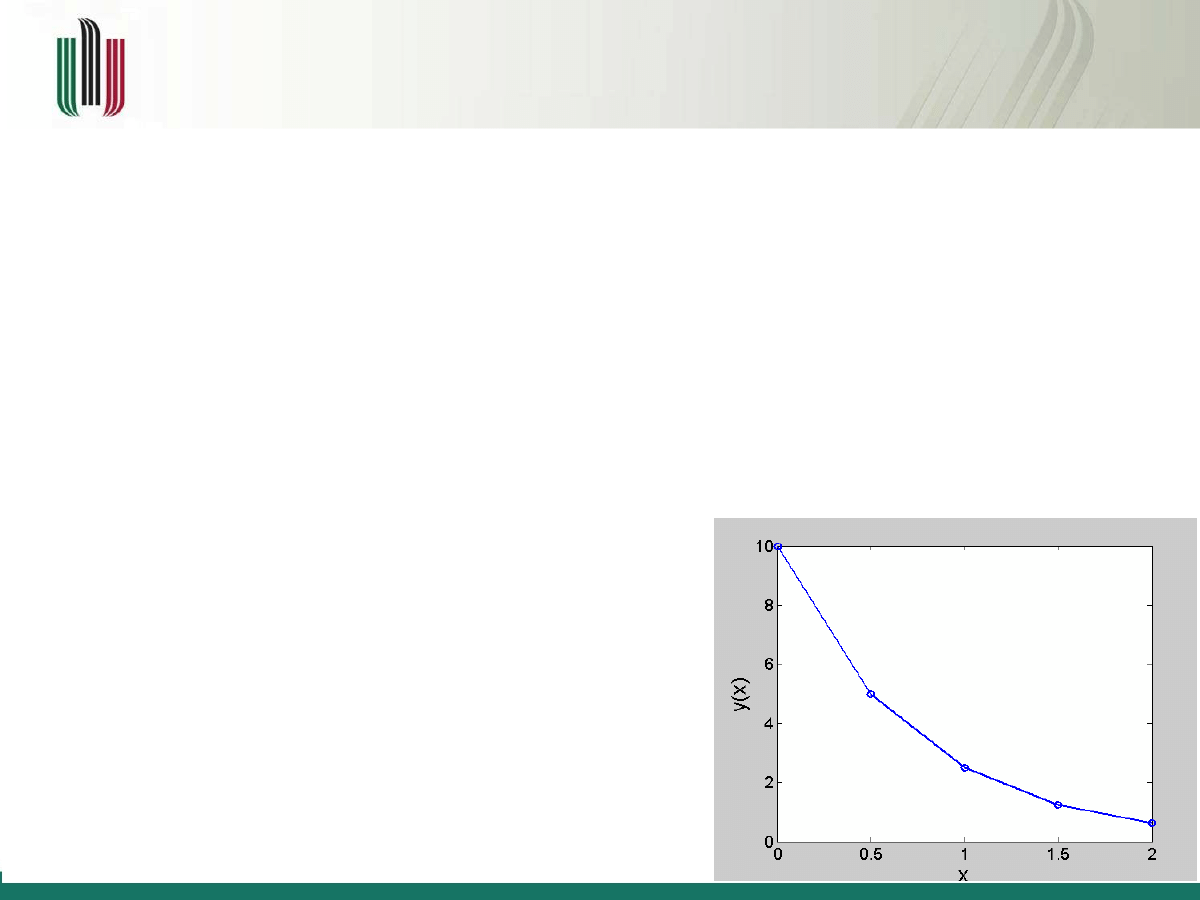
Dla pierwszego kroku obliczeń (i=1):

10

10

1

25

,

0

0

0

0

1

=

⋅

⋅

−

=

⋅

⋅

+

=

y

a

h

y

y

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

22

Rozwiązywanie równań różniczkowych

pierwszego rzędu

Dla pierwszego kroku obliczeń (i=1):

10

10

1

25

,

0

0

0

0

1

=

⋅

⋅

−

=

⋅

⋅

+

=

y

a

h

y

y

Dla drugiego kroku obliczeń (i=2):

5

10

1

5

,

0

10

1

1

2

=

⋅

⋅

−

=

⋅

⋅

+

=

y

a

h

y

y

Dla trzeciego kroku obliczeń (i=3):

25

,

0

5

1

25

,

0

5

2

2

3

=

⋅

⋅

−

=

⋅

⋅

+

=

y

a

h

y

y

Dla czwartego kroku obliczeń (i=4):

0.625

10

1

25

,

0

25

,

0

3

3

4

=

⋅

⋅

−

=

⋅

⋅

+

=

y

a

h

y

y

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

23

Rozwiązywanie równań różniczkowych

pierwszego rzędu

Dla pierwszego kroku obliczeń (i=1):

10

10

1

25

,

0

0

0

0

1

=

⋅

⋅

−

=

⋅

⋅

+

=

y

a

h

y

y

Dla drugiego kroku obliczeń (i=2):

5

10

1

5

,

0

10

1

1

2

=

⋅

⋅

−

=

⋅

⋅

+

=

y

a

h

y

y

Dla trzeciego kroku obliczeń (i=3):

25

,

0

5

1

25

,

0

5

2

2

3

=

⋅

⋅

−

=

⋅

⋅

+

=

y

a

h

y

y

Dla czwartego kroku obliczeń (i=4):

0.625

10

1

25

,

0

25

,

0

3

3

4

=

⋅

⋅

−

=

⋅

⋅

+

=

y

a

h

y

y

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

24

Rozwiązywanie równań różniczkowych

wyższych rzędów

Przedstawione wcześniej metody pozwalają na rozwiązywanie równań różniczkowych
zwyczajnych I rzędu. Równanie różniczkowe wyższego rzędu można rozwiązać po
sprowadzaniu go do układu równań różniczkowych rzędu I

W przypadku rozwiązywania równań różniczkowych wyższego rzędu

równanie zostaje sprowadzone do układu równań rzędu I przy wykorzystaniu metody

podstawienia zmiennych. Stosując notację

równoważny układ równań przybiera postać

(

)

( )

)

1

(

0

0

)

1

(

0

0

0

0

)

1

(

)

(

)

(

,...,

'

)

(

'

,

,

,...,

'

,

,

−

−

−

=

=

=

=

n

n

n

n

y

x

y

y

x

y

y

x

y

y

y

y

x

f

y

)

1

(

3

2

1

,

....

,

''

,

'

,

−

=

=

=

=

n

n

y

y

y

y

y

y

y

y

(

)













=

=

=

n

n

y

y

y

x

f

y

y

y

y

y

,...,

,

,

'

...

'

'

2

1

3

2

2

1

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

25

Rozwiązywanie równań różniczkowych

wyższych rzędów

Jest to równanie różniczkowe zwyczajne rzędu II. Aby je
sprowadzić do układu dwóch równań różniczkowych rzędu I
dzielimy je stronami przez m

( )

t

F

kx

x

b

x

m

=

+

+ &

&

&

( )

m

t

F

x

m

k

x

m

b

x

=

+

+

&

&

&

Równanie ruchu opisujące ten układ ma postać:

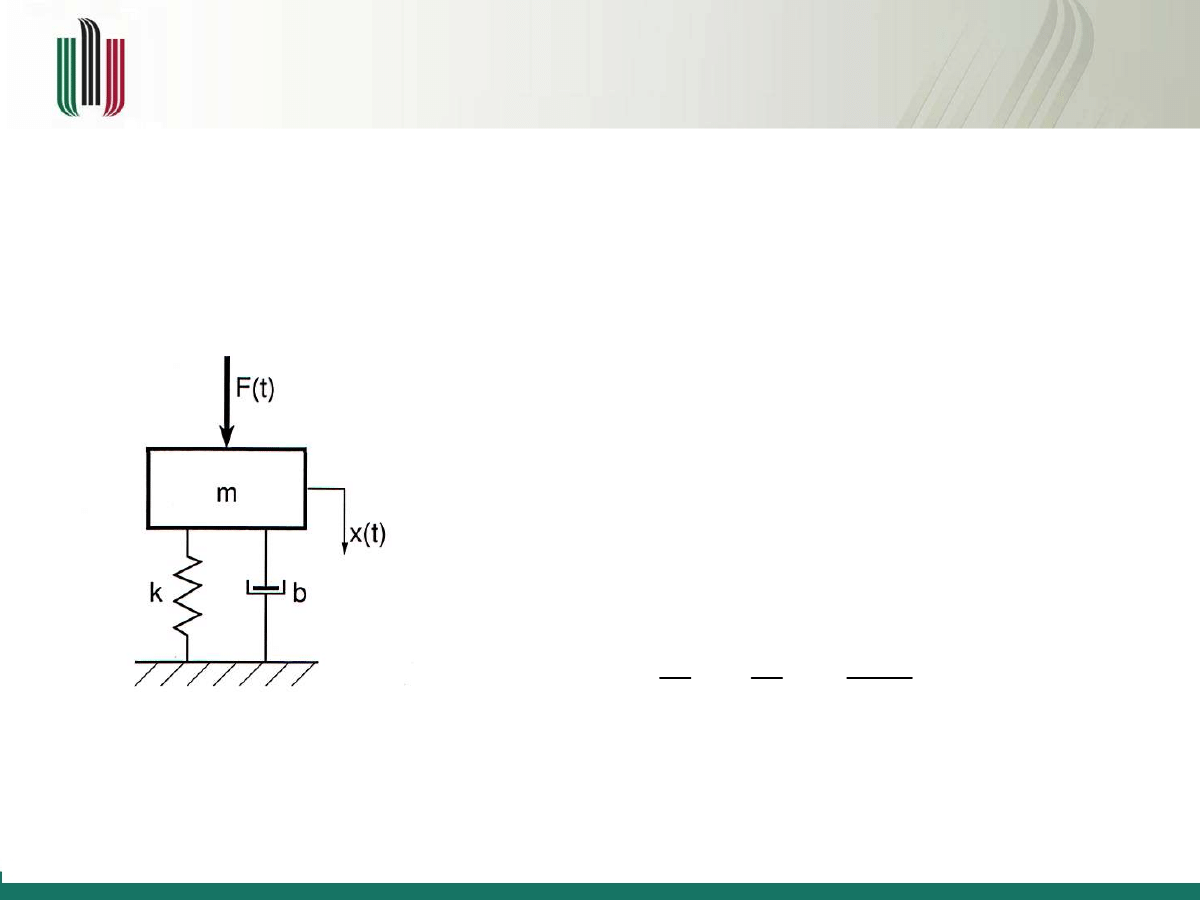
Przykład 2

Rozpatrzmy układ drgający o jednym stopniu swobody

x

(t), masie

m

, współczynniku

sprężystości

k

, współczynniku tłumienia

b

. Wymuszeniem jest siła harmoniczna

F(t)=F·sin(ωt)

, gdzie

F

oznacza amplitudę,

ω

– częstość drgań

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

26

Rozwiązywanie równań różniczkowych

wyższych rzędów

Po lewej stronie pozostawiamy najwyższą pochodną

x

Dokonujemy następującego podstawienia:

Równanie różniczkowe można zapisać jako układ dwóch równań rzędu I:

Układ równań zapisany w postaci macierzowej:

B

X

A

X

+

⋅

=

&

( )

m

t

F

x

m

k

x

m

b

x

+

−

−

=

&

&

&







=

=

2

1

1

x

x

x

x

&









+

−

−

=

=

m

t

F

x

m

b

x

m

k

x

x

x

)

(

2

1

2

2

1

&

&

















+













⋅

















−

−

=













m

t

F

x

x

m

b

m

k

x

x

)

(

0

1

0

2

1

2

1

&

&

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

27

Zastosowanie funkcji środowiska MATLAB do

rozwiązywania równań różniczkowych

Aby rozwiązać układ przy pomocy funkcji środowiska Matlab należy:

1.

Napisać m-plik funkcyjny zwracający wartości funkcji

f

(

x, t

) zapisanej macierzowo jako ,w którym:

Dane: Masa

m = 1 [kg],

sprężystość

k = 100,

tłumienie

b = 0,1. W

ymuszenie

–

siła

harmoniczna

F (t) = F·sin(ωt)

o amplitudzie

F = 1 [N].

Szukane jest przemieszczenie

x

masy

m

w okolicy częstości rezonansowej układu w przedziale czasu

[t

0

= 0, t

k

= 10 ]

przy

zadanych warunkach początkowych

x

0

= 0, x’

0

= 0

X

&

B

X

A

X

+

⋅

=













=

2

1

x

x

&

&

&

,

)

(

0

,

,

1

0

2

1

















=













=

















−

−

=

m

t

F

x

x

m

b

m

k

B

X

A

,

2. Napisać m-plik skryptowy definiujący warunki początkowe oraz rozwiązujący równanie

różniczkowe, w którym:

•

Określony jest przedział argumentów rozwiązania [t

0

, t

k

]

•

Wprowadzone są warunki początkowe

x

0

, x’

0

•

Rozwiązane jest układ równań zapisany w pliku funkcyjnym przy wykorzystaniu funkcji
środowiska (ode23, ode45)

•

Przedstawione jest rozwiązanie w postaci wykresu funkcji x(t)

• Przyjęte zostają stałe parametry opisujące układ

m

,

k

,

F

,

b

• Na podstawie wyznaczonego wcześniej układu równań różniczkowych (zapisanego w postaci
macierzowej) obliczane są wartości prawej strony równania

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

28

Zastosowanie funkcji środowiska MATLAB do

rozwiązywania równań różniczkowych

[X,Y] = solver(odefun,tspan,y0,options)

Składnia funkcji (ode23, ode45,…) rozwiązującej równania różniczkowe zwyczajne (ODE –

ang. ordinary

differential equations

) rzędu I jest następująca (w MATLAB 6.5):

gdzie solver oznacza nazwę funkcji reprezentującej algorytm rozwiązania. Funkcje ode23 i ode45
korzystają z par metod Rungego-Kutty odpowiednio: rzędu 2 i 3 (ode23) oraz 4 i 5 (ode45). Funkcje te
zwracają wektor Y stanowiący rozwiązanie równania oraz X – wektor argumentów funkcji, który wyznaczany
jest adaptacyjnie na podstawie założonej tolerancji błędu

odefun – odwołanie pośrednie do funkcji znajdującej się po prawej stronie równania różniczkowego przy
pomocy znaku @, na przykład - @nazwa, gdzie nazwa oznacza nazwę funkcji

tspan - wektor określający granice przedziału w którym rozwiązywane jest równanie [x0 xk]

y0 – wektor określający warunki początkowe y(x0)

options – opcjonalny parametr zawierający parametry całkowania, stworzony przy pomocy funkcji odeset

options = odeset('name1',value1,'name2',value2,...)

Łańcuch tekstowy 'name1', 'name2',… określa parametr, natomiast value1, value2,… jego wartość.
Przykładowo za ’name1’, ’name2’,… można przyjąć

AbsTol – określający tolerancję błędu bezwzględnego, domyślna wartość to 1·10

-6

RelTol – określający tolerancję błędu względnego, domyślna wartość to 1·10

-3

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

29

Zastosowanie funkcji środowiska MATLAB do

rozwiązywania równań różniczkowych

W celu stworzenia pliku funkcyjnego o nazwie NazwaFunkcji.m w oknie poleceń (Command
Window) należy wpisać

>> edit NazwaFunkcji

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

30

Zastosowanie funkcji środowiska MATLAB do

rozwiązywania równań różniczkowych

Otwarte zostaje okno edytora, w którym należy umieścić kod pliku funkcyjnego

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

31

Zastosowanie funkcji środowiska MATLAB do

rozwiązywania równań różniczkowych

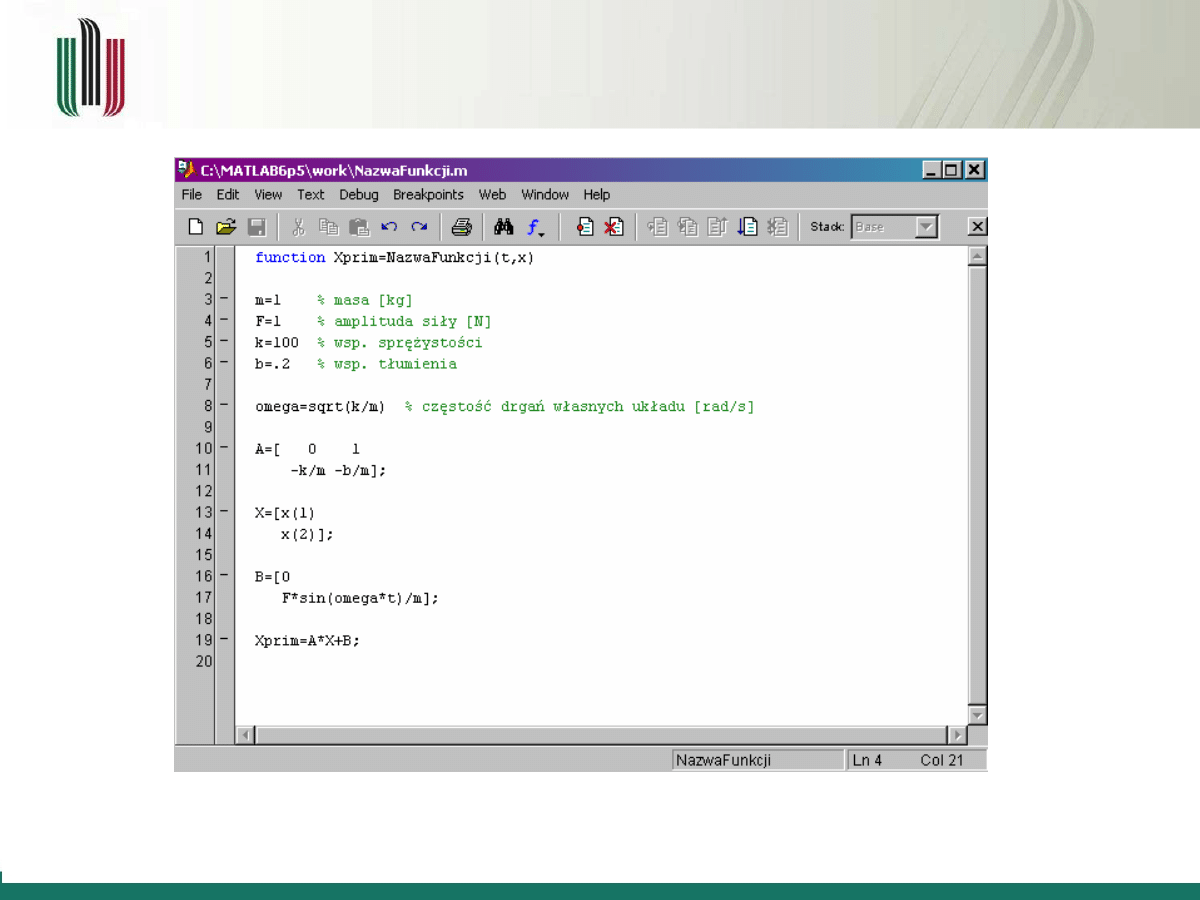
function

Xprim = NazwaFunkcji(t,x)

m=1

% masa [kg]

F=1

% amplituda siły [N]

k=100

% wsp. sprężystości

b=.2

% wsp. tłumienia

omega=sqrt(k/m)

% częstość [rad/s]

A=[ 0 1

-k/m -b/m];

X=[ x(1)

x(2)];

B=[ 0

F*sin(omega*t)/m];

Xprim=A*X+B;

% wynik

Wyrażenie definiujące funkcję o nazwie
NazwaFunkcji w której parametry wejściowe to
t, x oraz parametrem wyjściowym jest Xprim

Przyjęcie stałych parametrów równania

Przyjęcie częstości wymuszenia równej
częstości drgań własnych układu

Wprowadzenie macierzy opisujących równanie
ruchu układu

Obliczenie Xprim

m-plik funkcjny – NazwaFunkcji.m

opis

Kolor zielony

– komentarz

Kolor niebieski

– wyrażenie Matlab

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

32

Zastosowanie funkcji środowiska MATLAB do

rozwiązywania równań różniczkowych

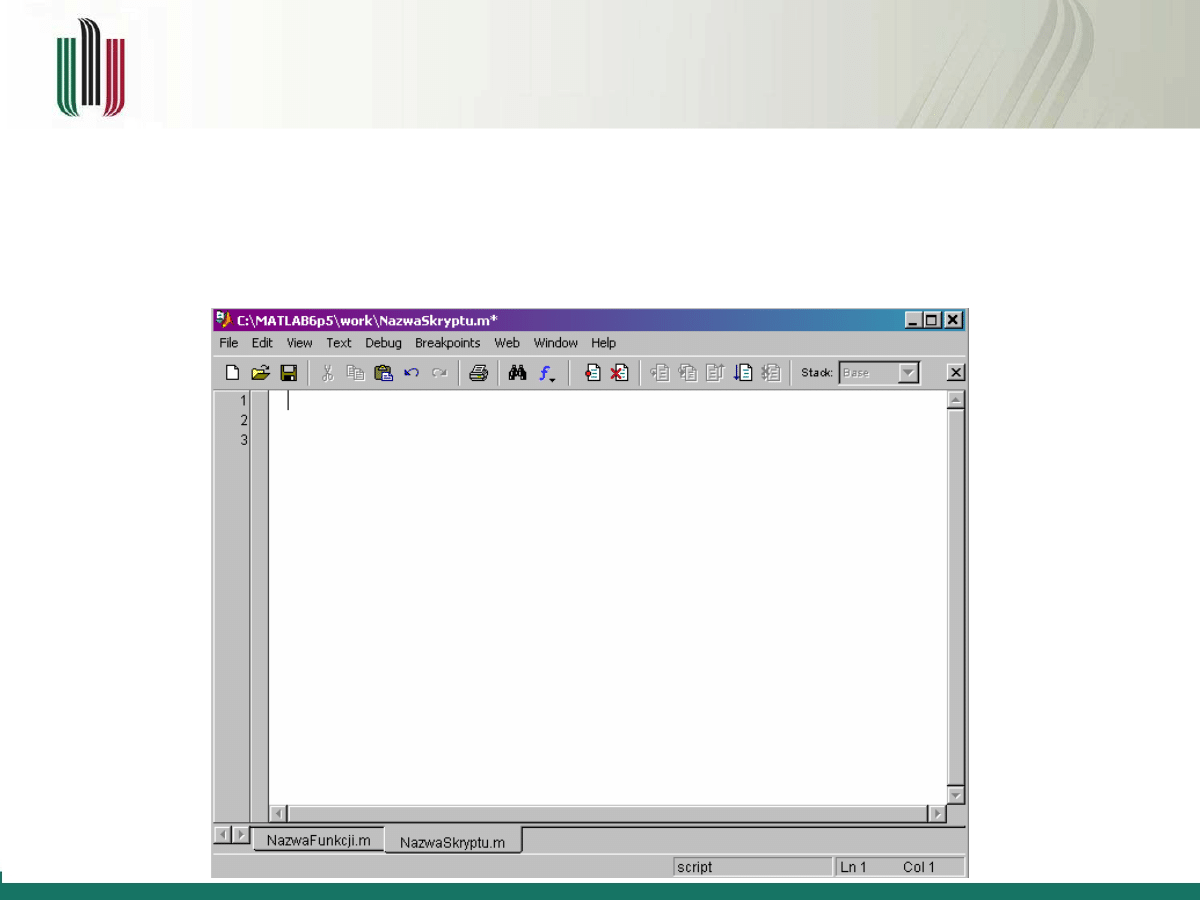
Po wprowadzeniu kodu plik należy zapisać w katalogu roboczym File -> Save (lub Ctr+S)

Ważne! Nazwa podana przy definiowaniu funkcji musi być nazwą m-pliku

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

33

Zastosowanie funkcji środowiska MATLAB do

rozwiązywania równań różniczkowych

W celu stworzenia pliku skryptowego o nazwie NazwaSkryptu w oknie poleceń należy wpisać

>> edit NazwaSkryptu

co powoduje, że w kolejnej zakładce otwarty jest nowy plik tekstowy o nazwie NazwaSkryptu

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

34

Zastosowanie funkcji środowiska MATLAB do

rozwiązywania równań różniczkowych

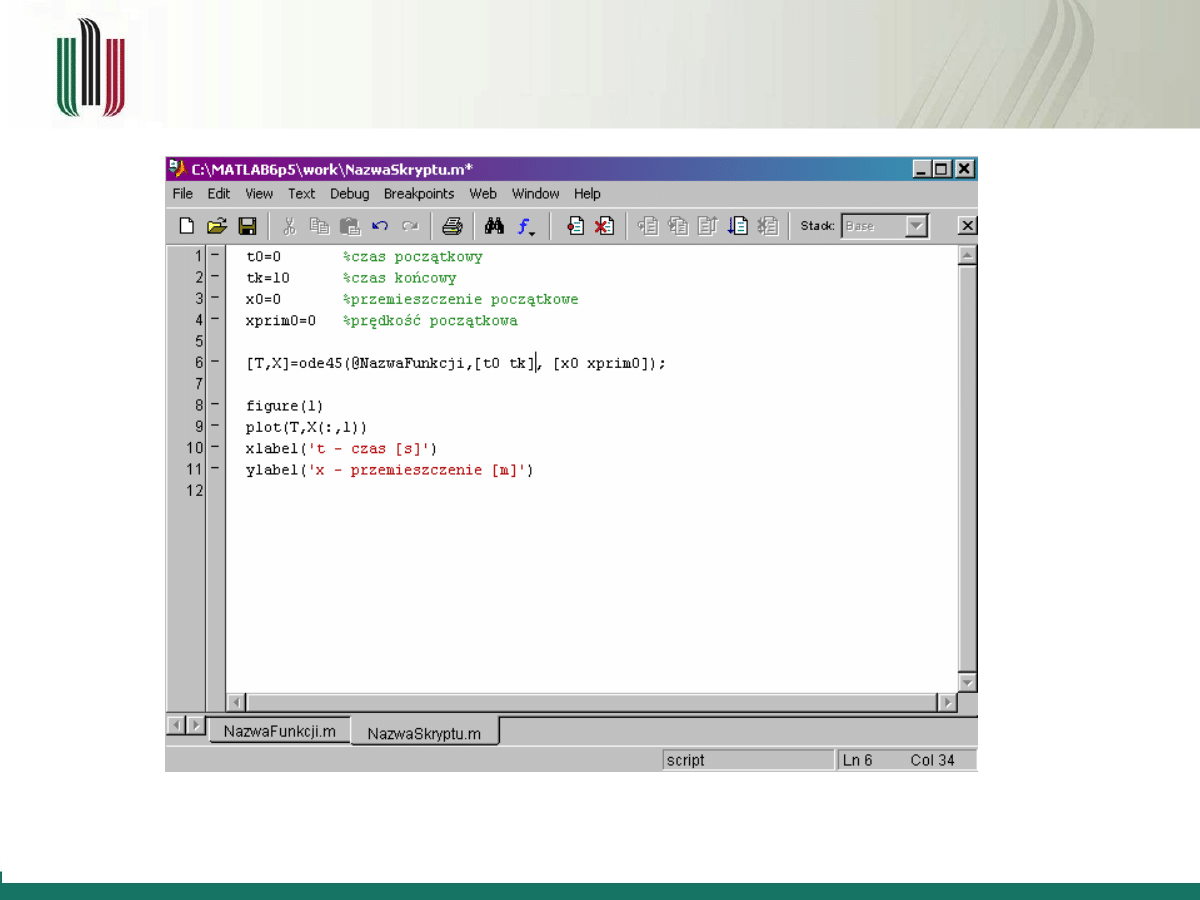
t0=0

%czas początkowy

tk=10

%czas końcowy

x0=0

%przemieszczenie początkowe

xprim0=0

%prędkość początkowa

[T,X]=ode45(@NazwaFunkcji,[t0 tk],...

[x0 xprim0]);

figure(1)

%nowe okno graficzne

plot(T,X(:,1))

%wykres funkcji x(t)

xlabel(

't - czas [s]'

)

ylabel(

'x - przemieszczenie [m]'

)

Przyjęcie przedziału czasu oraz parametrów
początkowych równania

Rozwiązanie równania różniczkowego przy
pomocy funkcji ode45, przy ustawieniach
domyślnych dla funkcji zapisanej w pliku
NazwaFunkcji.m

Otworzenie okna graficznego. Narysowanie
wykresu funkcji przemieszczeń x(t)

Opisanie osi wykresu

m-plik skryptowy – NazwaSkryptu.m

opis

Kolor zielony

– komentarz

Kolor czerwony

– łańcuch tekstowy

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

35

Zastosowanie funkcji środowiska MATLAB do

rozwiązywania równań różniczkowych

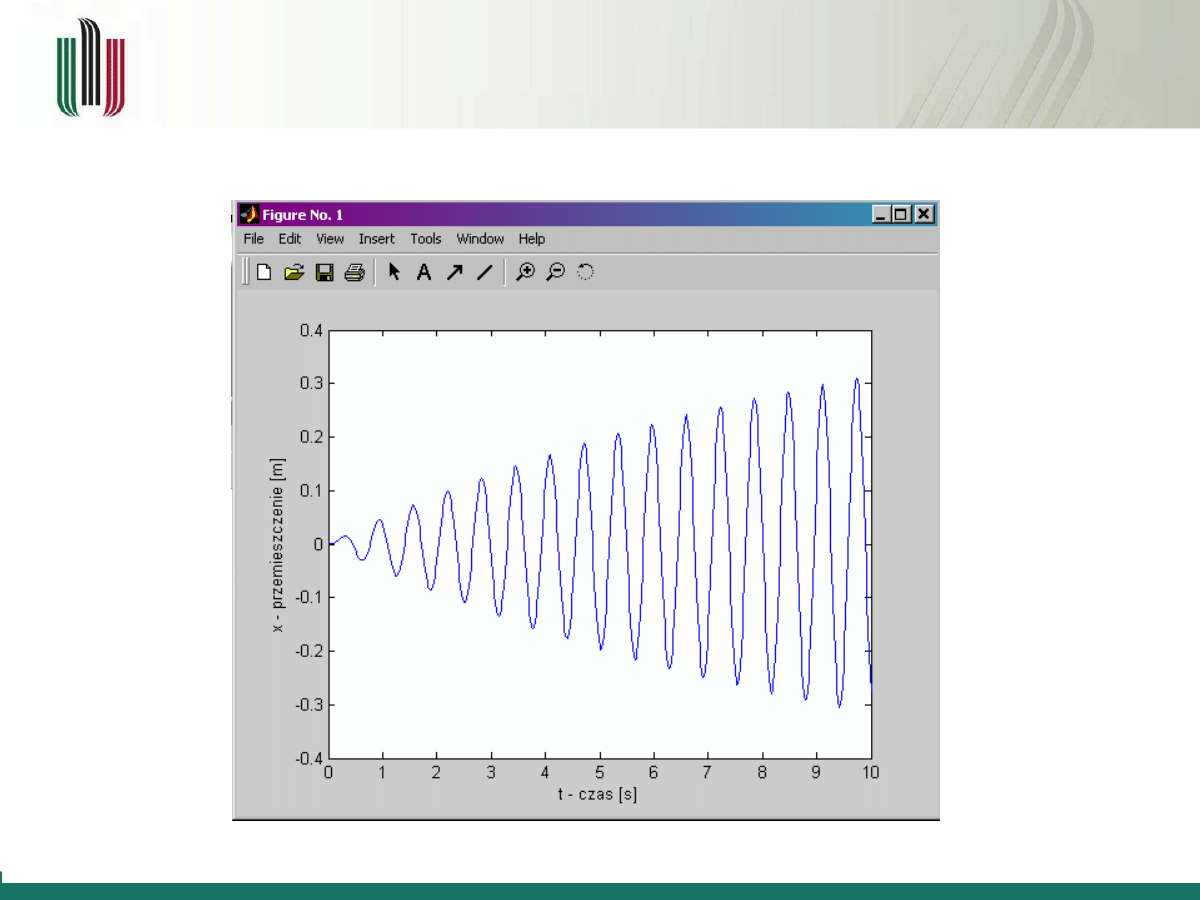
Po wprowadzeniu kodu plik należy zapisać w katalogu roboczym File -> Save (lub Ctr+S)

Program uruchamia się wybierając w menu Debug -> Run (lub klawisz funkcyjny F5)

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

36

Zastosowanie funkcji środowiska MATLAB do

rozwiązywania równań różniczkowych

Efektem działania programu jest wykres przemieszczeń x w zależności od czasu t

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

39

W roku 1956 Newmark zaproponował rodzinę metod umożliwiających jednokrokowe
rozwiązywanie liniowych dynamicznych równań ruchu o postaci

Przy założeniu obliczeń w chwilach czasu

∆t, 2∆t, 3∆t,

… rozwinięcie wyrażenia

x

t

oraz

w szereg Taylora w punkcie

t

prowadzi do uzyskania równań:

Bezpośrednie całkowanie równań ruchu.

Metoda Newmarka

t

t

t

t

F

Kx

x

C

x

M

=

+

+ &

&

&

( )

( )

...

6

2

3

2

+

∆

+

∆

+

∆

+

=

∆

−

∆

−

∆

−

∆

−

t

t

t

t

t

t

t

t

t

t

t

t

x

x

x

x

x

&

&

&

&

&

&

( )

...

2

2

+

∆

+

∆

+

=

∆

−

∆

−

∆

−

t

t

t

t

t

t

t

t

t

x

x

x

x

&

&

&

&

&

&

&

( )

( )

t

t

t

t

t

t

t

t

t

t

t

t

∆

−

∆

−

∆

−

∆

−

∆

+

∆

+

∆

+

=

x

x

x

x

x

&

&

&

&

&

&

3

2

2

β

( )

t

t

t

t

t

t

t

t

t

∆

−

∆

−

∆

−

∆

+

∆

+

=

x

x

x

x

&

&

&

&

&

&

&

2

γ

Jeżeli zakładamy, że przyspieszenie jest liniowe w przedziale długości kroku, można

zapisać zależność

t

t

t

t

t

∆

−

=

−

∆

−

1

x

x

x

&

&

&

&

&

&

&

Newmark obciął pozostałe wyrazy szeregu, wprowadził współczynniki

β

i

γ

oraz zapisał

równania w postaci:

t

x

&

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

40

Metoda Newmarka

Po podstawieniu otrzymywane są równania

t

t ∆

−

x

&

&

&

( )

( )

t

t

t

t

t

t

t

t

t

t

t

x

x

x

x

x

&

&

&

&

&

2

2

2

1

∆

+

∆











 −

+

∆

+

=

∆

−

∆

−

∆

−

β

β

t

t

t

t

t

t

t

t

x

x

x

x

&

&

&

&

&

&

∆

+

∆

−

+

=

∆

−

∆

−

γ

γ

)

1

(

( )

( )

t

t

t

t

t

t

t

t

t

t

t

t

t

∆

−

∆

+

∆

+

∆

+

=

−

∆

−

∆

−

∆

−

)

(

2

1

3

2

x

x

x

x

x

x

&

&

&

&

&

&

&

β

( )

t

t

t

t

t

t

t

t

t

t

∆

−

∆

+

∆

+

=

−

∆

−

∆

−

)

(

1

2

x

x

x

x

x

&

&

&

&

&

&

&

&

γ

Po przekształceniach, otrzymywane są standardowe równania Newmarka

Zależności te można rozwiązać rekurencyjnie dla każdego kroku czasowego, dla każdego

stopnia swobody układu będącego przemieszczeniem. Wyraz wyznacza się z równania
ruchu po podzieleniu jego obu stron przez masę

t

x

&

&

M

F

x

M

K

x

M

C

x

t

t

t

t

=

+

+

&

&

&

t

t

t

t

x

M

K

x

M

C

M

F

x

−

−

=

&

&

&

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

41

Metoda Newmarka – bezpośrednie rozwiązanie

równań w pojedynczym kroku

Równania Newmarka można przekształcić do postaci

(

)

(

)

t

t

t

t

t

t

t

t

t

t

t

t

t

t

t

t

b

b

b

b

b

b

∆

−

∆

−

∆

−

∆

−

∆

−

∆

−

+

+

−

=

+

+

−

=

x

x

x

x

x

x

x

x

x

x

&

&

&

&

&

&

&

&

&

&

&

6

5

4

3

2

1

( )

(

)

γ

γ

γ

γ

β

β

β

−

+

∆

=

∆

+

=

∆

=

−

=

∆

−

=

∆

=

3

6

2

5

1

4

3

2

2

1

1

,

1

,

,

2

1

1

,

1

,

1

b

t

b

t

b

b

tb

b

b

t

b

t

b

gdzie poszczególne współczynniki wynoszą

Po podstawieniu do równania ruchu układu otrzymuje się zależność

t

t

t

t

F

Kx

x

C

x

M

=

+

+ &

&

&

(

)

(

)

t

t

t

t

t

t

t

t

t

t

t

t

t

t

b

b

b

b

b

b

b

b

∆

−

∆

−

∆

−

∆

−

∆

−

∆

−

−

−

+

−

−

+

=

+

+

x

x

x

C

x

x

x

M

F

x

K

C

M

&

&

&

&

&

&

6

5

4

3

2

1

4

1

)

(

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

42

Stabilność metody Newmarka

β

γ

ω

β

γ

−

≤

≤

≥

2

1

oraz

2

1

,

2

1

max

∆t

2

1

2

≥

≥

γ

β

W przypadku zerowego tłumienia metoda Newmarka jest warunkowo stabilna jeżeli

gdzie

ω

max

jest maksymalną częstością układu strukturalnego

Metoda Newmarka jest bezwarunkowo stabilna jeżeli spełniony jest warunek

Jednak w momencie gdy

γ

jest większa niż

0,5

wprowadzone zostają błędy związane z

„tłumieniem numerycznym” oraz „wydłużaniem okresu czasu”

Zazwyczaj przyjmuje się

2

1

,

4

1

=

=

β

γ

Metody numeryczne i statystyka - Rozwiązywanie równań różniczkowych

43

Metoda Newmarka – algorytm obliczeń

Dla układu o jednym stopniu swobody o masie

M

, sztywności

K

, tłumieniu

C

przy wymuszeniu siłą

F

t

1. Obliczenia wstępne

1. Przyjąć wartości

M

,

K

i

C

2. Przyjąć parametry całkowania

β

oraz

γ

3. Obliczyć współczynniki (stałe całkowania)

b

1

, b

2

, b

2

, b

3

, b

4

, b

5

, b

6

4. Wyznaczyć efektywną sztywność

5. Przyjąć warunki początkowe:

2. Obliczenia dla każdego kroku czasu:

1. Obliczyć efektywne wymuszenie

2. Wyznaczyć przemieszczenie dla czasu t

3. Obliczyć przyspieszenie i prędkość dla czasu t

4. Przejść do kroku 2.1 wraz z

t = t + ∆t

0

0

0

,

,

x

x

x

&

&

&

,...

3

,

2

,

t

t

t

t

∆

∆

∆

=

C

M

K

K

4

1

b

b

+

+

=

)

(

)

(

6

5

4

3

2

1

t

t

t

t

t

t

t

t

t

t

t

t

t

t

b

b

b

b

b

b

∆

−

∆

−

∆

−

∆

−

∆

−

∆

−

−

−

+

−

−

+

=

x

x

x

C

x

x

x

M

F

F

&

&

&

&

&

&

K

F

F

K

t

t

t

t

x

x

=

⇒

=

(

)

(

)

t

t

t

t

t

t

t

t

t

t

t

t

t

t

t

t

b

b

b

b

b

b

∆

−

∆

−

∆

−

∆

−

∆

−

∆

−

+

+

−

=

+

+

−

=

x

x

x

x

x

x

x

x

x

x

&

&

&

&

&

&

&

&

&

&

&

6

5

4

3

2

1