Rozwiązywanie liniowych równań różniczkowych zwyczajnych za pomocą przekształcenia Laplace'a

Doniosła rola przekształcenia Laplace'a polega m.in. na tym, że daje ono prostą metodę rozwiązywania równań różniczkowych, polegająca na ich algebraizacji.

Niech będzie dane liniowe równanie różniczkowe o stałych współczynnikach

(1)

gdzie
- znana funkcja zmiennej rzeczywistej t.

Dane są ponadto warunki początkowe:
;
;...;
.

Rozwiązując równanie typu (1) należy:

1. poddać je przekształceniu Laplace'a z uwzględnieniem warunków początkowych,

2. wyznaczyć transformatę
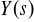
   szukanego rozwiązania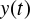
   ,

3. doprowadzić tę transformatę do postaci
   ,

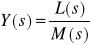
4. wyznaczyć poszukiwane rozwiązanie
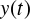
   , będące oryginałem transformaty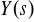
   :

.

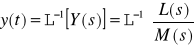
Zadanie 1.

Rozwiązać równanie

dla warunków początkowych
;
.

Rozwiązanie

Obie strony równania poddajemy przekształceniu Laplace'a, uwzględniając przy tym warunki początkowe.

Wyróżnik trójmianu mianownika transformaty
, a więc mianownik transformaty posiada dwa pierwiastki pojedyncze i rzeczywiste:

;
;
.

Rozkładając transformatę na ułamki proste mamy:

Z warunku tożsamości mamy:

Po podstawieniu za
, otrzymamy:

; stąd
.

Podobnie, dla

; stąd
.

A zatem transformata rozwiązania
ma postać:

Rozwiązanie
.

Zadanie 2.

Rozwiązać równanie

dla warunków początkowych
.

Rozwiązanie

Po transformacji Laplace'a obu stron równania oraz po uwzględnieniu warunków początkowych otrzymamy:

stąd

Wyróżnik trójmianu

, co oznacza, że mianownik transformaty
ma pierwiastki zespolone. Wobec tego rozkład
na ułamki proste wygląda następująco:

.

Po sprowadzeniu do wspólnego mianownika, mamy:

Po podstawieniu
otrzymamy

, stąd
.

Podstawiając
oraz wyznaczoną wcześniej wartość A, otrzymamy dwa równania z niewiadomymi B i C.

I tak, dla

stąd

Dla
mamy

stąd
.

A zatem
, skąd
;
.

Po podstawieniu wyliczonych powyżej wartości współczynników A, B, C oraz po uwzględnieniu, że
, transformata rozwiązania
przybiera postać:

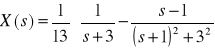
Przekształcamy drugi człon transformaty, do postaci dogodnej dla wyznaczenia oryginału:

Po uwzględnieniu powyższych przekształceń, transformata
ma postać:

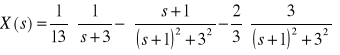
Rozwiązanie równania

.

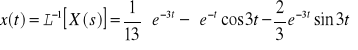
Zadania do samodzielnego rozwiązania

Zadanie 1

Wyznaczyć transformatę Laplace'a funkcji:

a)

b)

c)

Odp. a)

b)

c)

Zadanie 2

Wyznaczyć oryginały transformat:

a)

Odp.

b)

Odp.

Zadanie 3

Rozwiązać równanie różniczkowe
dla warunków początkowych
;
.

Odp.
.

Zadanie 4

Rozwiązać równanie różniczkowe
dla warunków początkowych
;
.

Odp.

Zadanie 5

Rozwiązać równanie różniczkowe
dla warunków początkowych
.

Odp.

Zadanie 6

Rozwiązać równanie różniczkowe
dla warunków początkowych
.

Odp.
.

Zadanie 7

Rozwiązać równanie różniczkowe
dla warunków początkowych
.

Odp.

5