GM-M1-132

U

k

ad

g

ra

fi

cz

n

y

©

C

K

E

2

0

1

1

UZUPE NIA ZESPÓ

NADZORUJ

CY

miejsce

na naklejkę

z kodem

UZUPE NIA UCZEŃ

dysleksja

WI

I

201

Czas pracy:

90 minut

KOD UCZNIA

PESEL

EGZ

IN

W KLASIE TRZECIEJ GIMNAZJUM

CZĘŚĆ MATEMATYCZNO-PRZYRODNICZA

MATEMATYKA

Instrukcja dla ucznia
1.

Sprawd , czy zestaw zada zawiera 12 stron (zadania 1–23).

Ewentualny brak stron lub inne usterki zg o nauczycielowi.

2.

Ze rodka zestawu wyrwij strony od 7. do 10. przeznaczone na rozwi zania

zada od 21. do 23. i brudnopis.

3.

Na pierwszej stronie zestawu wpisz swój kod i numer PESEL.

4.

Na karcie odpowiedzi wpisz swój kod i numer PESEL, wype nij matryc

znaków.

5.

Na stronie 7. wpisz swój kod i PESEL. Na stronach 8.–10. wpisz swój kod.

6.

Czytaj uwa nie wszystkie teksty i zadania. Wykonuj zadania zgodnie

z poleceniami.

7.

Rozwi zania zada zapisuj d ugopisem lub piórem z czarnym tu-

szem/atramentem. Nie u ywaj korektora.

8.

W arkuszu znajduj si ró ne typy zada . Rozwi zania zada od 1. do 20.

zaznaczaj na karcie odpowiedzi w nast puj cy sposób:

 wybierz jedn z podanych odpowiedzi i zamaluj kratk z odpowiadaj -

c jej liter , np. gdy wybra e odpowied A:

 wybierz w a ciw odpowied i zamaluj kratk z odpowiednimi literami,

np. gdy wybra e odpowied FP lub NT:

lub

 do informacji oznaczonych w a ciw liter dobierz informacje ozna-

czone liczb lub liter i zamaluj odpowiedni kratk , np. gdy wybra-

e liter B i liczb 1 lub litery NB:

lub

9.

Staraj si nie pope niać błędów przy zaznaczaniu odpowiedzi, ale jeśli się

pomylisz, błędne zaznaczenie otocz kółkiem i zaznacz inną odpowiedź, np.

10.

Rozwiązania zadań od 21. do 23. zapisz czytelnie i starannie w wyznaczo-

nych miejscach na stronach 7., 8. i 9. Pomyłki przekreślaj.

11.

Rozwiązując zadania, możesz wykorzystać miejsce opatrzone napisem

Brudnopis

(strona 10.). Zapisy w brudnopisie nie będą sprawdzane i oce-

niane.

12.

Po zakończeniu pracy z zestawem włóż strony z rozwiązaniami zadań od

21. do 23. do środka zestawu.

Powodzenia!

Centralna Komisja Egzaminacyjna

Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu.

Strona 2 z 12

10 lat

14 lat

15 lat

16 lat

0%

20%

40%

60%

80%

100%

10 lat

25%

14 lat

15%

15 lat

20%

16 lat

40%

I

ń 2.

W tabeli przedstawiono informacje dotycz ce wieku wszystkich uczestników obozu
narciarskiego.

Wiek uczestnika Liczba uczestników

10 lat

5

14 lat

3

15 lat

4

16 lat

8

Zadanie 1. (0–1)

ń

t

,

y

y

Mediana wieku uczestników obozu jest równa

A. 14 lat.

B. 14,5 roku.

C. 15 lat.

D. 15,5 roku.

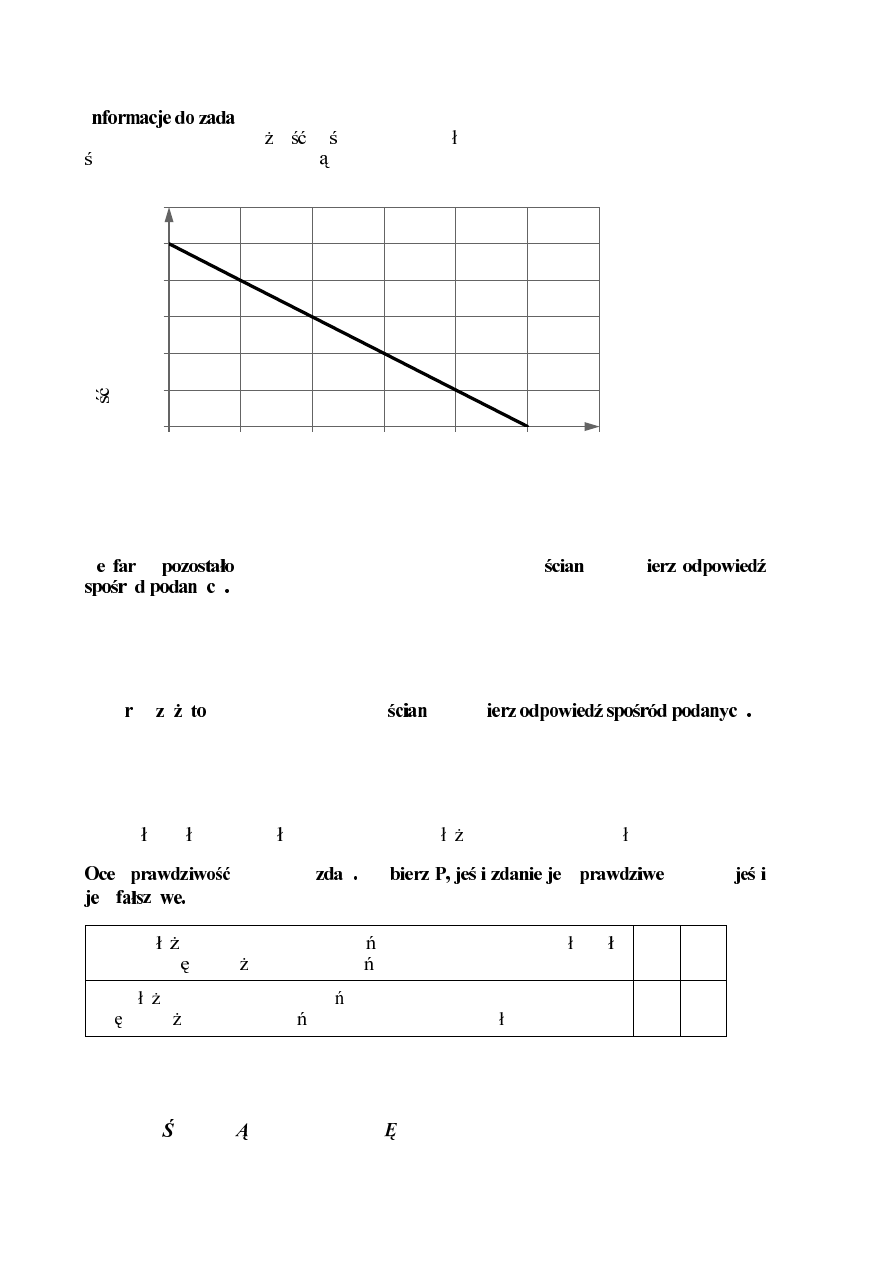
Zadanie 2. (0–1)
Na którym diagramie poprawnie przedstawiono procentowy

u

k

u

gl

u

Wyb

h

PRZENIE ROZWI ZANIA NA KART ODPOWIEDZI!

40%

15%

20%

25%

0%

20%

40%

60%

80% 100%

10 lat

14 lat

15 lat

16 lat

25%

20%

15%

40%

0%

20%

40%

60%

80%

100%

10 lat

14 lat

15 lat

16 lat

A.

B.

C.

D.

Strona 3 z 12

Zadanie 3. (0–1)
W pewnej hurtowni za 120 jednakowych paczek herbaty trzeba zap aci 1500 z .

Ile takich paczek h b ty

ku

t hu t

, przy tej samej cenie za

k ? Wyb

h

A. 48

B. 50

C. 52

D. 56

Zadanie 4. (0–1)
Cena brutto = cena netto + podatek VAT

ń

y

ń Wy

P,

l

st

, lub F –

l

st

y

Je eli cena netto 1 kg jab ek jest równa 2,50 z , a cena brutto jest równa 2,70 z ,
to podatek VAT wynosi 8% ceny netto.

P

F

Je eli cena netto podr cznika do matematyki jest równa 22 z , to cena tej

ksi ki z 5% podatkiem VAT wynosi 24,10 z .

P

F

Zadanie 5. (0–1)

Il

liczb:

3

2

,

2

1

,

25

10

,

4

1

k

5

2

< x <

5

3

?

Wyb

h

A. Jedna liczba.

B. Dwie liczby.

C. Trzy liczby.

D. Cztery liczby.

Zadanie 6. (0–1)
Dane s liczby: a = (–2)

12

, b = (–2)

11

, c = 2

10

.

ń

t

,

y

y

Liczby te uporz dkowane od najmniejszej do najwi kszej to:

A. c, b, a.

B. a, b, c.

C. c, a, b.

D. b, c, a.

Zadanie 7. (0–1)
Dane s liczby x i y spe niaj ce warunki: x < 0 i y < x.

ń

y

ń Wy

l zdanie jest prawdziwe, lub F –

l

st

y

Liczba y jest ujemna.

P

F

Liczba x jest wi ksza od liczby y.

P

F

PRZENIE ROZWI ZANIA NA KART ODPOWIEDZI!

Strona 4 z 12

I

ń 8. i 9.

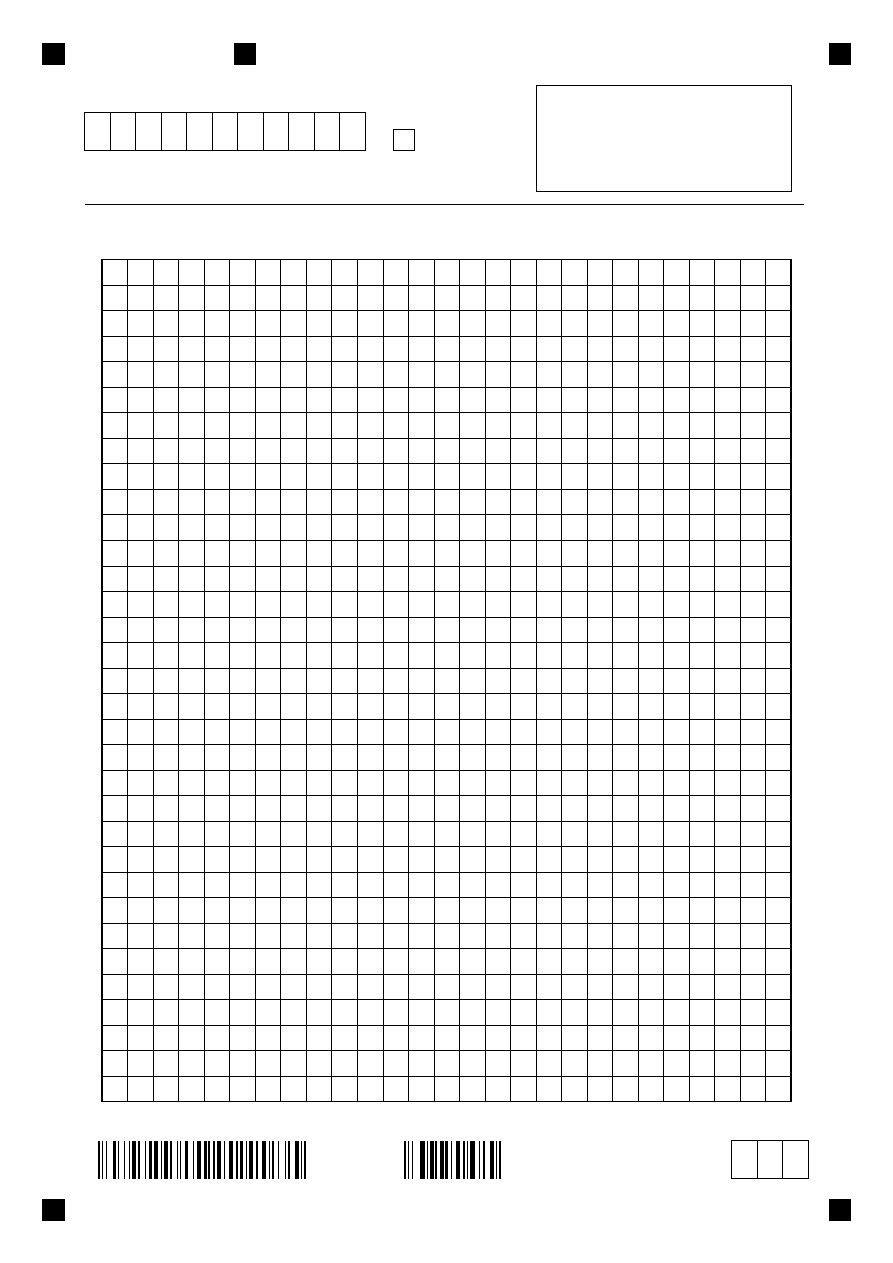
Wykres przedstawia zale no ilo ci farby pozosta ej w pojemniku (w litrach) od powierzchni

ciany (w m

2

) pomalowanej farb z tego pojemnika.

Zadanie 8. (0–1)
Il

by

w pojemniku po pomalowaniu 30 m

2

y? Wyb

ó

y h

A. 8 litrów

B. 12 litrów

C. 16 litrów

D. 20 litrów

Zadanie 9. (0–1)
Ile fa by u y na pomalowanie 10 m

2

y? Wyb

h

A. 4 litry

B. 8 litrów

C. 10 litrów

D. 16 litrów

Zadanie 10. (0–1)
W pude ku by o 20 kul bia ych i 10 czarnych. Do o ono jeszcze 10 kul bia ych i 15 czarnych.

ń

podanych

ń Wy

l

st

, lub F –

l

st

y

Przed do o eniem kul prawdopodobie stwo wylosowania kuli bia ej by o

trzy razy wi ksze ni prawdopodobie stwo wylosowania kuli czarnej.

P

F

Po do o eniu kul prawdopodobie stwo wylosowania kuli czarnej jest
wi ksze ni prawdopodobie stwo wylosowania kuli bia ej.

P

F

PRZENIE ROZWI ZANIA NA KART ODPOWIEDZI!

0

4

8

12

16

20

24

10

20

30

40

50

60

il

o

f

ar

by

w poje

mni

ku (

li

tr)

pomalowana powierzchnia (m

2

)

Strona 5 z 12

80 cm

50 cm

60 cm

Zadanie 11. (0–1)

rednia pr dko samochodu na trasie przebytej w czasie 4 godzin wynios a 60

h

km .

ń

h

ń Wyb

,

li zdanie jest prawdziwe, lub F –

l

st

y

Aby czas przejazdu by o 1 godzin krótszy, rednia pr dko samochodu

na tej trasie musia aby wynosi 80

h

km .

P

F

Gdyby rednia pr dko samochodu na tej trasie by a równa 40

h

km ,

to czas przejazdu by by równy 6 godzin.

P

F

Zadanie 12. (0–1)
Ania ma w skarbonce 99 z w monetach o nomina ach 2 z i

5 z . Monet dwuz otowych jest

2 razy wi cej ni pi cioz otowych.

ń

t

,

y

y

Je eli przez x oznaczymy liczb monet pi cioz otowych, a przez y – liczb monet
dwuz otowych, to podane zale no ci

opisuje uk ad równa

A.







99

5

2

2

y

x

x

y

B.







99

2

5

2

y

x

x

y

C.







99

2

5

2

y

x

y

x

D.







99

5

2

2

y

x

y

x

Zadanie 13. (0–1)

W prostopad o ciennym akwarium, o wymiarach podanych na rysunku, woda si ga

3

2

jego

wysoko ci.








Ile litrów wody jest w akwarium? Wyb

y h

A. 16000 litrów

B. 1600 litrów

C. 160 litrów

D. 16 litrów

PRZENIE ROZWI ZANIA NA KART ODPOWIEDZI!

Strona 6 z 12

A

K

D

B

C

L

A

B

C

Zadanie 14. (0–1)
W równoleg oboku ABCD bok AB jest

dwa razy

d u szy od boku AD.
Punkt K jest rodkiem boku AB, a punkt L jest

rodkiem boku CD.

ń

y

ń Wy

l

st

, lub F –

l

st

y

Trójk t ABL ma takie samo pole, jak trójk t ABD.

P

F

Pole równoleg oboku ABCD jest cztery razy wi ksze od pola trójk ta AKD.

P

F

Zadanie 15. (0–1)
Punkt B jest rodkiem okr gu. Prosta AC jest styczna do okr gu w punkcie C, |AB| = 20 cm
i |AC| = 16 cm.

ń

t

,

y

y

Promie BC okr gu ma d ugo

A. 12 cm

B. 10 cm

C. 4 cm

D. 2 cm

Zadanie 16. (0–1)
Jeden z k tów wewn trznych trójk ta ma miar

α

, drugi ma miar o 30° wi ksz ni k t

α

,

a trzeci ma miar trzy razy wi ksz ni k t

α

.

ń

t

,

y

y

Trójk t ten jest

A. równoboczny.

B. równoramienny.
C. rozwartok tny.

D. prostok tny.

PRZENIE ROZWI ZANIA NA KART ODPOWIEDZI!

Miejsce na rozwi¹zania zadañ od 21. do 23.

KOD UCZNIA

PESEL

Miejsce na naklejkê

z kodem

(PESEL i identyfikator szko³y)

Rozwi¹zanie zadania 21.

Zapisy na marginesie poza ramk¹ nie bêd¹ oceniane. Zapisy na marginesie poza ramk¹ nie bêd¹ oceniane.

Zapisy na marginesie poza ramk¹ nie bêd¹ oceniane. Zapisy na marginesie poza ramk¹ nie bêd¹ oceniane.

Zapisy na marginesie poza ramk¹ ni

e bêd¹ ocen

iane.

Zapisy na marginesie poza ramk¹ nie bêd

¹ oceniane.

Zapisy na marginesie poza ramk¹ nie b

êd¹ oceniane.

Zapisy na ma

rginesie poza ramk¹ nie bêd¹

oceniane.

GM-M1-132

Strona 7 z 12

dysleksja

Rozwi¹zanie zadania 22.

Zapisy na marginesie poza ramk¹ nie bêd¹ oceniane. Zapisy na marginesie poza ramk¹ nie bêd¹ oceniane.

Zapisy na marginesie poza ramk¹ nie bêd¹ oceniane. Zapisy na marginesie poza ramk¹ nie bêd¹ oceniane.

Zapisy na marginesie poza ramk¹ nie b

êd¹ oceniane.

Zapisy na marginesie poza ramk¹ nie bêd¹

oceniane.

Zapisy na marginesie poza ramk¹ n

ie bêd¹ oceniane.

Zapisy na marginesie poza ramk¹ nie bê

d¹ oceniane.

KOD UCZNIA

GM-M1-132

Strona 8 z 12

A

B

C

D

E

F

Rozwi¹zanie zadania 23.

Zapisy na marginesie poza ramk¹ nie bêd¹ oceniane. Zapisy na marginesie poza ramk¹ nie bêd¹ oceniane.

Zapisy na marginesie poza ramk¹ nie b

êd¹ oceniane.

Zapisy na marginesie poza ramk¹ nie bêd¹

oceniane.

Zapisy na marginesie poza ramk¹ n

ie bêd¹ oceniane.

Zapisy na marginesie poza ramk¹ nie bê

d¹ oceniane.

Zapisy na marginesie poza ramk¹ nie bêd¹ oceniane. Zapisy na marginesie poza ramk¹ nie bêd¹ oceniane.

KOD UCZNIA

GM-M1-132

Strona 9 z 12

BRUDNOPIS

Zapisy w brudnopisie nie bêd¹ oceniane. Zapisy w brudnopisie nie bêd¹ oceniane.

Zapisy w brudnopisie nie bê

d¹ oceniane.

Zapisy w brudnopisie nie bêd¹

oceniane.

Zapisy w brudnopisie nie bê

d¹ oceniane.

Zapisy w brudnopisie nie bêd¹

oceniane.

Zapisy w brudnopisie nie bêd¹ oceniane. Zapisy w brudnopisie nie bêd¹ oceniane.

KOD UCZNIA

GM-M1-132

Strona 10 z 12

Strona 11 z 12

Zadanie 17. (0–1)
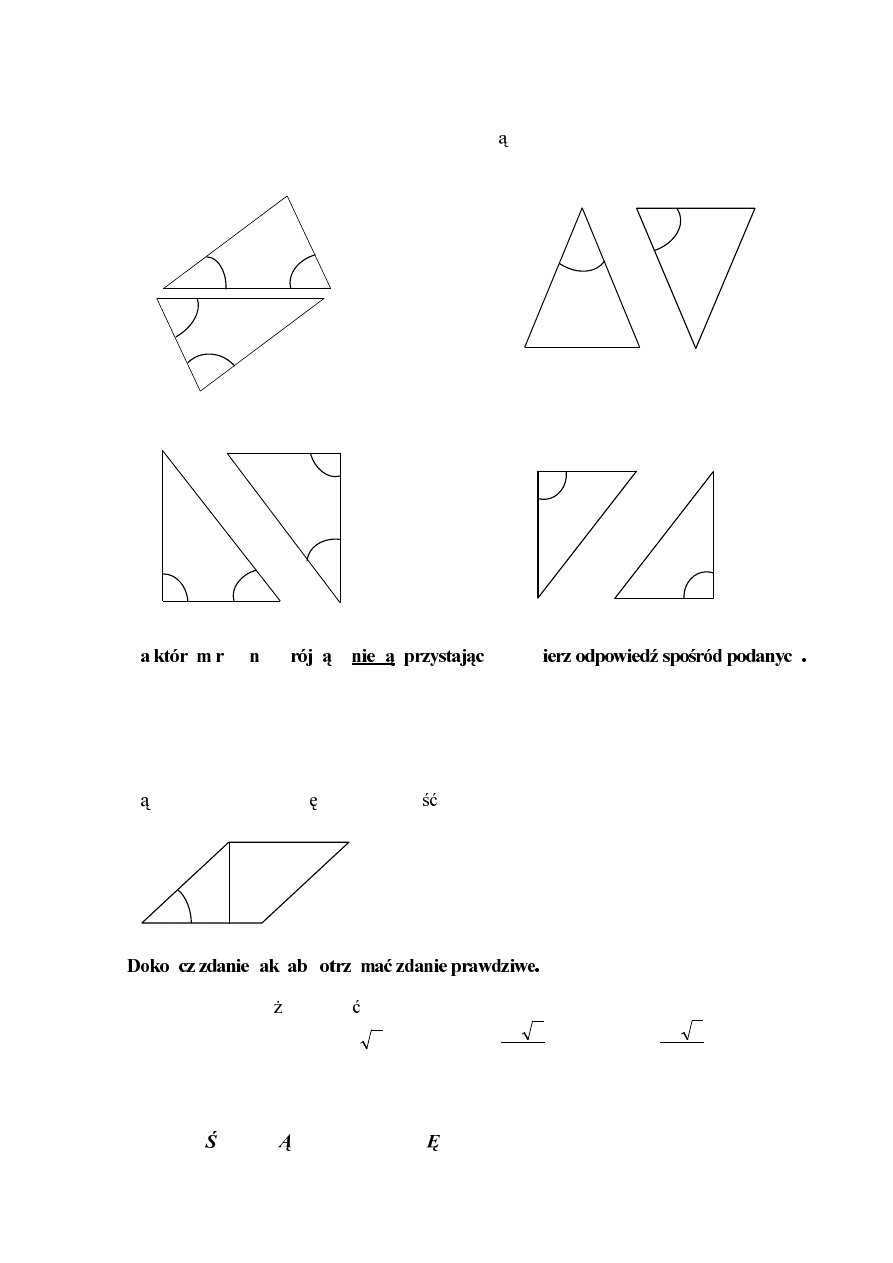
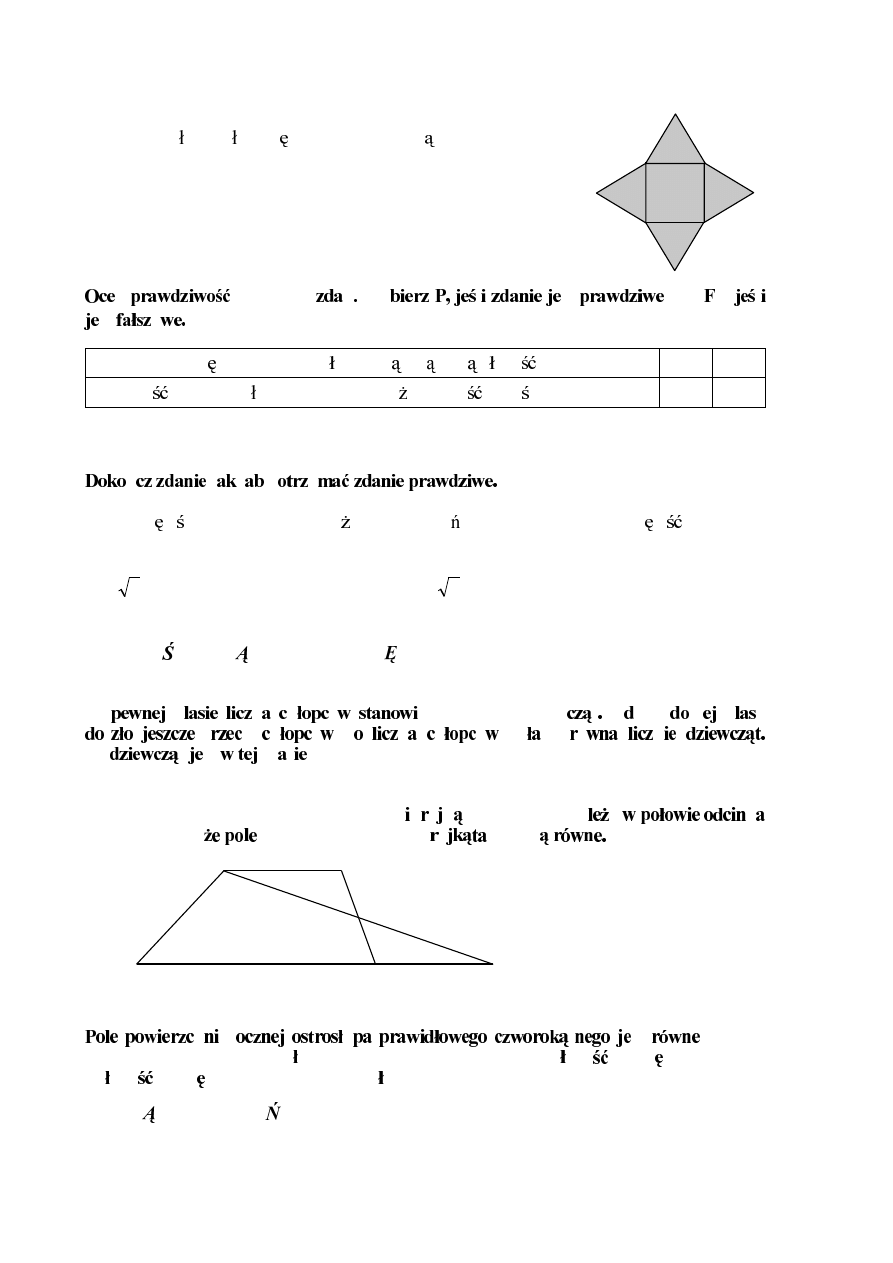
Na rysunkach I–IV przedstawiono cztery pary trójk tów.

I

II

III

IV

N

y ysu ku t

k ty

s

A. I

B. II

C. III

D. IV

e? Wyb

h

Zadanie 18. (0–1)
K t ostry rombu ma miar 45º, a wysoko rombu jest równa h.

ń

t

,

y

y

Pole tego rombu mo na wyrazi wzorem

A. P =

2

h

B. P =

2

2

h

C. P =

2

2

2

h

D. P =

4

3

2

h

PRZENIE ROZWI ZANIA NA KART ODPOWIEDZI!

45º

h

37°

65°

4

65°

78°

4

44°

4

4

68°

4

4

52°

5

.

41°

5

.

5

3

.

4

5

.

Strona 12 z 12

Zadanie 19. (0–1)
Siatka ostros upa sk ada si z kwadratu i trójk tów równobocznych
zbudowanych na bokach tego kwadratu.

ń

podanych

ń Wy

l

st

, lub –

l

st

y

Wszystkie kraw dzie tego ostros upa maj tak sam d ugo .

P

F

Wysoko tego ostros upa jest mniejsza ni wysoko jego ciany bocznej.

P

F

Zadanie 20. (0–1)

ń

t

,

y

y

Suma obj to ci 8 kul, z których ka da ma promie 1, jest taka sama jak obj to jednej kuli
o promieniu

A.

3

8

B. 8

C.

2

2

D. 2

PRZENIE ROZWI ZANIA NA KART ODPOWIEDZI!

Zadanie 21. (0–3)
W

k

b h

ó

80% liczby dziew

t G yby

t k

y

s

t

h h

ó , t

b h

ó by by ó

b

Ile

t st

kl s ? Zapisz obliczenia.

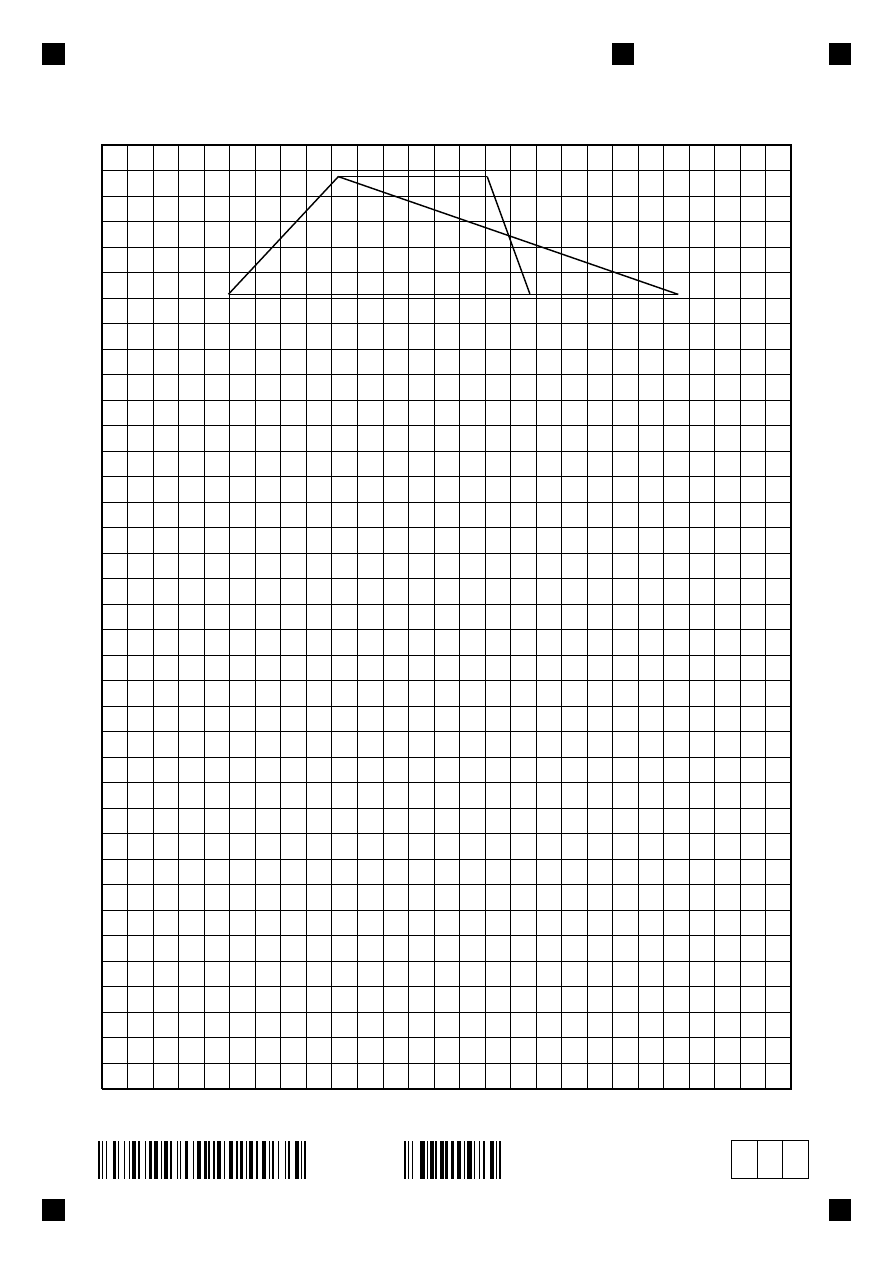
Zadanie 22. (0–2)
Na rysunku przedstawiono trapez ABCD t ó k t AFD. Punkt E

y

k

BC

. Uzasadnij,

trapezu ABCD i pole t ó

AFD s

Zadanie 23. (0–4)

h b

u

t

st

80 cm

2

,

a pole jego powierzchni ca kowitej wynosi 144 cm

2

. Oblicz d ugo kraw dzi podstawy

i d ugo kraw dzi bocznej tego ostros upa. Zapisz obliczenia.

ROZWI ZANIA ZADA

OD 21. DO 23. ZAPISZ W WYZNACZONYCH MIEJSCACH

NA STRONACH 7., 8. I 9.

A

B

C

D

E

F