
Obliczenia z wykorzystaniem równowagi w roztworach

Obliczenia w roztworach
Jakie są składniki roztworu?
Które reakcje dysocjacji przebiegają
całkowicie (100% dysocjacji)?
Które reakcje osiągają stan
równowagi?
Które z reakcji równowagowych jest
dominująca i determinuje pH
roztworu?

Obliczenia w roztworach
1.
Utwórz listę składników roztworu
2.
Wskaż reakcje, które przebiegają całkowicie bez ustalania równowagi
(mocny kwas lub zasada)
Dla tej reakcji określ
Stężenia produktów
Wypisz główne składniki roztworu po reakcji
3.
Określ, który z głównych składników roztworu jest kwasem i zasadą
4.
Na podstawie wartości stałych równowag dla reakcji z kwasami i
zasadami określ, która z reakcji równowagowych będzie kontrolować
pH
5.
Dla dominującej reakcji utwórz wyrażenie na stałą równowagi
6.
Wypisz stężenia początkowe składników roztworu
7.
Określ zmianę, jaka musiała nastąpić, aby mógł być osiągnięty stan
równowagi
8.
Stosując wielkość określającą zmianę określ stężenia równowagowe
9.
Wstaw równania określające stężenia równowagowe do wyrażenia na
stałą równowagi
10.
Rozwiąż równanie w sposób przybliżony zakładając niewielką zmianę
11.
Sprawdź stopień dysocjacji. Jeżeli α<5% to rozwiązanie można uznać
za dokładne. Jeżeli α>5% powtórz obliczenia w sposób dokładny lub
iteracyjnie
Algorytm

Obliczenia - równowagi w
roztworach
Oblicz stopień dysocjacji i pH 1.00 dm
3
0.010 M roztworu
CH
3
COOH. Stała K
a
dla tego kwasu w temperaturze 25
o
C
wynosi 1.8·10
-5
.
H
2
O, CH
3
COOH – składniki roztworu
14
3
2
2
5
3
3
2
3
10
10
8
.
1
−
−
+
−
+
−
=
+
↔
+
⋅
=
+
↔
+
w
a
K
OH
O
H
O
H
O
H
K
O
H
COO
CH
O
H
COOH
CH
]
[
]
][
[
3
3
3
COOH
CH
O
H
COO
CH
K
a
+
−
=
Przyk
Przyk
ł
ł
ad 1 s
ad 1 s
ł
ł
aby kwas
aby kwas
5
3
3
2
3
10
8
.
1
−
+
−
⋅
=
+
↔
+
a
K
O
H
COO
CH
O
H
COOH
CH
Obliczenia - równowagi w
roztworach
Stan początkowy
0.01
0
0
Zmiana
-x
+x
+x
Równowaga
0.01-x
x
x
4
7
5
2
5
2
10
24
.
4
10
8
.
1
10
8
.
1
01
.
0
01
.
0
01
.
0
10
8
.
1
01
.
0
−
−
−
−
⋅
=
⋅
=
⋅
⋅
=
≅
−
⋅
=
−
=
x
x
x
x
x
K
a
+
−
+
↔
+
O
H
COO
CH
O
H
COOH
CH
3
3
2
3
Przyk
Przyk
ł
ł
ad 1 s
ad 1 s
ł
ł
aby kwas
aby kwas

Obliczenia - równowagi w
roztworach
Przyk
Przyk
ł
ł
ad 1 s
ad 1 s
ł
ł
aby kwas
aby kwas
%
5
%
2
.
4
%
100
01
.
0
10
24
.
4
%
100
]
[
4
3
<
≅
⋅
=
⋅
=
−
COOH
CH
x
o
α
Cyfry znaczące wyniku
Specyfika funkcji logarytmicznej
37
.
3
])
log([
10
24
.
4
]
[
3
3
4
3
=
−
=
⋅
=
=
+
−
+
O
H
pH
dm
mol
O
H
x

Obliczenia - równowagi w
roztworach
C
o
= 0.10 mol/dm
3
Przyk
Przyk
ł
ł
ad 1 s
ad 1 s
ł
ł
aby kwas
aby kwas
Stan początkowy
0.1
0
0
Zmiana
-x
+x
+x
Równowaga
0.1-x
x
x
+
−
+
↔
+
O
H
COO
CH
O
H
COOH
CH
3
3
2
3
3
6
5
2
5
2
10
34
.
1
10
8
.
1
10
8
.
1
1
.
0
1
.
0
1
.
0
10
8
.
1
1
.
0
−
−
−
−
⋅
=
⋅
=
⋅
⋅
=
≅
−
⋅
=
−
=
x
x
x
x
x
K
a

Obliczenia - równowagi w
roztworach
Przyk
Przyk
ł
ł
ad 1 s
ad 1 s
ł
ł
aby kwas
aby kwas
87
.
2
])
log([
10
34
.
1
]
[
%
5
%
3
.
1
%
100
1
.
0
10
34
.
1
%
100
]
[
3
3
4
3
3
3
=
−
=
⋅
=
=
<
≅
⋅
=
⋅
=
+
−
+
−
O
H
pH
dm
mol
O
H
x
COOH
CH
x
o
α
cyfry znaczące wyniku!!!
Obliczenia - równowagi w
roztworach
C
o
,
mol/dm
3
[H
3
O
+
],
mol/dm
3
α, %
0.00001
1.3·10
-5
134
0.0001
4.2 ·10
-5
42
0.001
1.3 ·10
-4
13
0.01
4.2 ·10
-4
4.2
0.1
1.3 ·10
-3
1.3
1
4.2 ·10
-3
0.42
Przyk
Przyk
ł
ł
ad 1 s
ad 1 s
ł
ł
aby kwas
aby kwas
rozwiązanie przybliżone
Założenie o małym
α
nie działa?

Obliczenia - równowagi w
roztworach
Przyk
Przyk
ł
ł
ad 1 s
ad 1 s
ł
ł
aby kwas
aby kwas
rozwiązania dokładne
0
2
4
lub
0
2
4
0
4
4
0
0
2
1
0
2
1
0
2
0
2
0
2
0
2
<
+
−
−
=
>
+
+
−
=
>
+
=
∆
+
=
∆
=
−
+
=
−
c
K
K
K
x
c
K
K
K
x
c
K
K
c
K
K
c
K
x
K
x
K
x
c
x
a
a
a
a
a
a
a
a
a
a
a
a
a
C
o
,
mol/dm
3
[H
3
O
+
],
mol/dm
3
α, %
0.00001
7.2·10
-6
72
0.0001
3.4·10
-5
34
0.001
1.3 ·10
-4
13
0.01
4.2 ·10
-4
4.2
0.1
1.3 ·10
-3
1.3
1
4.2 ·10
-3
0.42
Obliczenia - równowagi w
roztworach
Przyk
Przyk
ł
ł
ad 1 s
ad 1 s
ł
ł
aby kwas
aby kwas
rozwiązania dokładne
C
o
,
mol/dm
3
[H
3
O
+
],
mol/dm
3
α, %
0.00001
1.3·10
-5
134
0.0001
4.2 ·10
-5
42
0.001
1.3 ·10
-4
13
0.01
4.2 ·10
-4
4.2
0.1
1.3 ·10
-3
1.3
1
4.2 ·10
-3
0.42
rozwiązania przybliżone
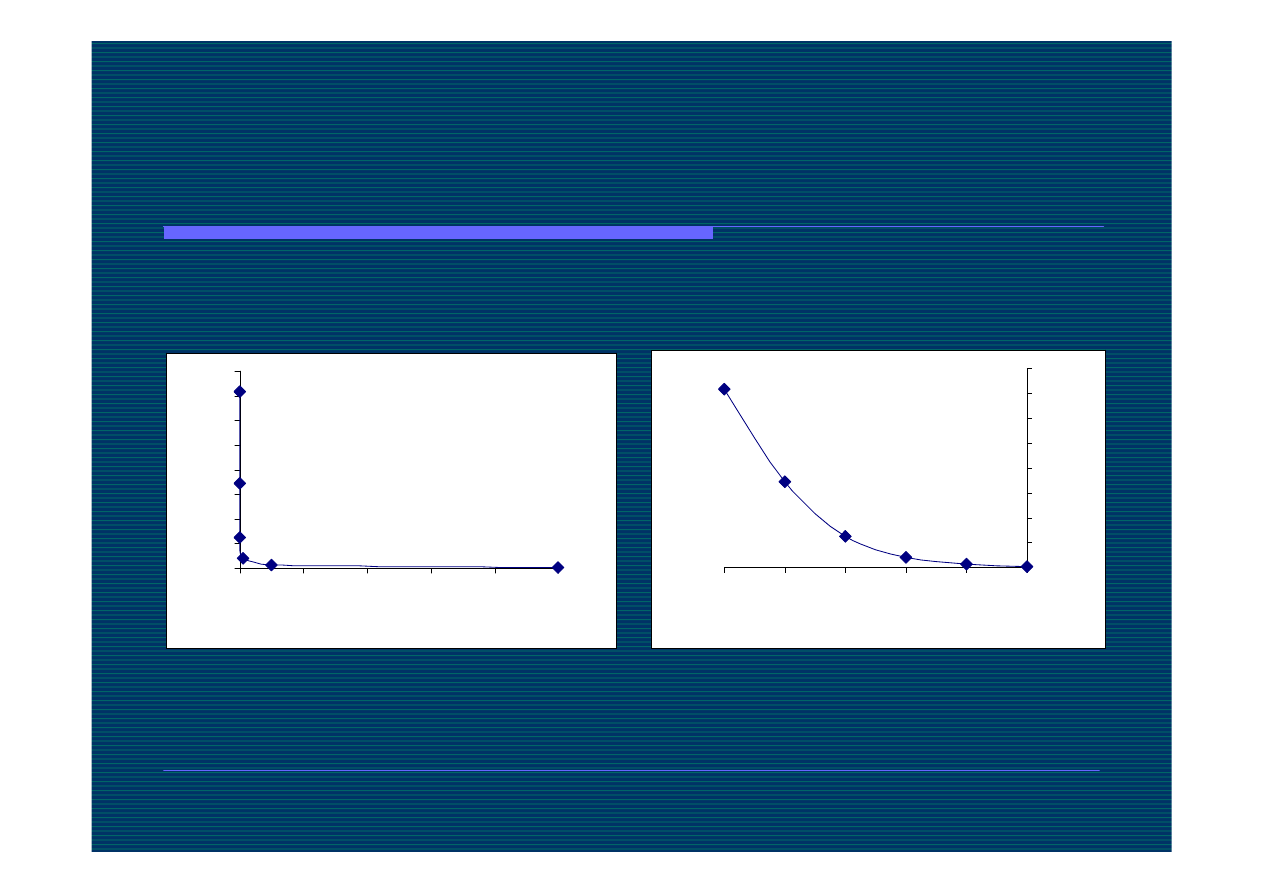
Zależność stopnia dysocjacji od
stężenia
0
10
20
30
40
50
60
70
80
1E-05 0.0001 0.001
0.01
0.1
1
c
0
, mol/dm3
α
, %
0
10
20
30
40
50
60
70
80
0
0.2
0.4
0.6
0.8
1
c
0
, mol/dm3
α
, %
Przyk
Przyk
ł
ł
ad 1 s
ad 1 s
ł
ł
aby kwas
aby kwas
w skali logarytmicznej
5
3
3
2
3
10
8
.
1
−
+
−
⋅
=
+
↔
+
a
K
O
H
COO
CH
O
H
COOH
CH
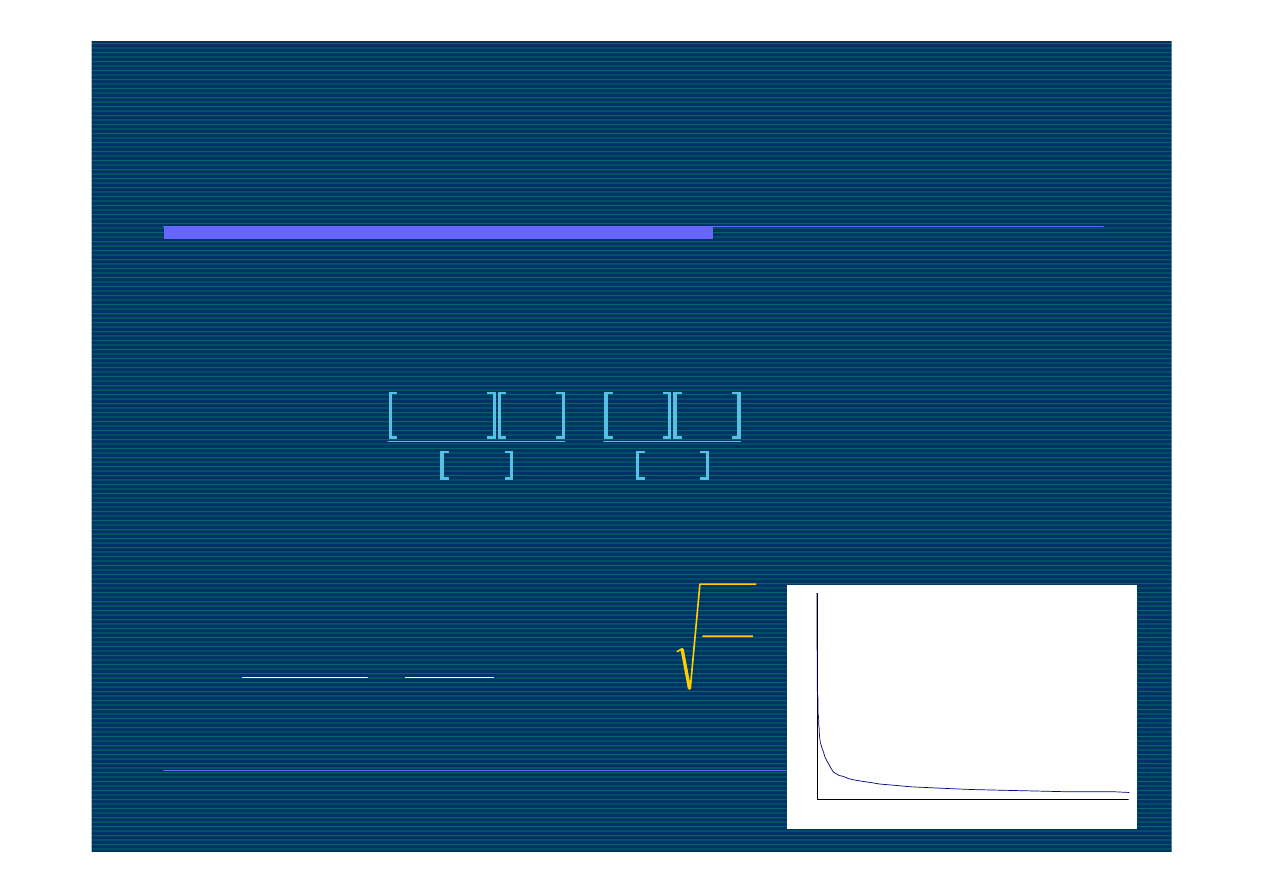
Zależność stopnia dysocjacji od
stężenia
HA
(aq)
+ H
2
O(l) ↔ H
3
O
(aq)
+ A
-
(aq)
(
)
α
α
α
α
α
α
α
−
⋅
=
−
⋅
=
−
=
⋅
−
=
⋅
=
=
+
−
1
)
1
(
)
1
(
]
[
]
[
]
[
2
0
0
2
0
0
0
0
0
3
c
c
c
K
c
c
c
HA
c
O
H
A
a
Prawo
Prawo
rozcie
rozcie
ń
ń
cze
cze
ń
ń
Ostwalda
Ostwalda
K
a
3
H O
A
H A
H
A
H A
=
=
+
−
+
−
0
2
0
1
c
K
i
c
K
a
a
=
<<
⋅
=
α
α
α
stężenie
st
o
p
ie
ń
d
ys
o
cj
ac
ji
a,
%

Obliczenia - równowagi w
roztworach
Przyk
Przyk
ł
ł
ad 1 s
ad 1 s
ł
ł
aby kwas i
aby kwas i
autodysocjacja
autodysocjacja
wody
wody
14
3
2
2
5
3
3
2
3
10
)
2
10
8
.
1
)
1
−
−
+
−
+
−
=
+
↔
+
⋅
=
+
↔
+
w
a
K
OH
O
H
O
H
O
H
K
O
H
COO
CH
O
H
COOH
CH
C
o
= 0.00000001 mol/dm
3
Stan początkowy
0.00000001
0 0
0
Zmiana
-x
1
+x
1
+x
1
+x
2
+x
2
Równowaga 0.00000001-x
1
x
1
x
1
+ x
2
x
2
−
+
−
OH
O
H
COO
CH
COOH
CH
3
3
3

Obliczenia - równowagi w
roztworach
Przyk
Przyk
ł
ł
ad 1 s
ad 1 s
ł
ł
aby kwas i
aby kwas i
autodysocjacja
autodysocjacja
wody
wody
C
o
= 0.000010 mol/dm
3
(
)
14
2
1
2
5
1
8
2
1
1
10
10
8
.
1
10
)
(
−
−
−
=
+
=
⋅
=
−
+
=
x
x
x
K
x
x
x
x
K
w
a
Rozwiązanie tego układu równań wymaga
zastosowania metod numerycznych

Stężenie
Temperatura
Rodzaj rozpuszczalnika
Wspólny jon
Czynniki wpływające na stopień
dysocjacji

Obliczenia - równowagi w
roztworach
Przyk
Przyk
ł
ł
ad 2 s
ad 2 s
ł
ł
aby kwas i mocny kwas
aby kwas i mocny kwas
Oblicz pH oraz stopień dysocjacji 1.00 dm
3
roztworu
zawierającego 0.010 mola CH
3
COOH oraz 0.010 mola
HCl. Oblicz stopień dysocjacji CH
3
COOH w tym
roztworze. Stała K
a
dla tego kwasu w temperaturze
25
o
C wynosi 1.8·10
-5
.
CH
3
COOH, HCl
−
+
−
+
−
+
→
+
⋅
=
+
↔
+
Cl
O
H
O
H
HCl
K
O
H
COO
CH
O
H
COOH
CH
a
3
2
5
3
3
2
3
10
8
.
1
]
[
]
][
[
3
3
3
COOH
CH
O
H
COO
CH
K
a
+
−
=

Obliczenia - równowagi w
roztworach
Stan początkowy
0.01 0
0.01
Zmiana
-x
+x
+x
Równowaga
0.01-x
x 0.01+x
(
)
3
5
5
/
10
8
.
1
01
.
0
01
.
0
01
.
0
01
.
0
10
8
.
1
01
.
0
01
.
0
dm
mol
x
x
i
x
x
x
x
K
a
−
−
⋅
=
≅
+
≅
−
⋅
=
−
+
=
+
−
+
↔
+
O
H
COO
CH
O
H
COOH
CH
3
3
2
3
Przyk
Przyk
ł
ł
ad 2 s
ad 2 s
ł
ł
aby kwas i mocny kwas
aby kwas i mocny kwas

%
18
.
0
%
100
01
.
0
10
8
.
1
%
100
]
[
5
3
≅
⋅
=
⋅
=
−
COOH
CH
x
o
α
Obliczenia - równowagi w
roztworach
Przyk
Przyk
ł
ł
ad 2 s
ad 2 s
ł
ł
aby kwas i mocny kwas
aby kwas i mocny kwas
Pod wpływem dodatku HCl stopień
dysocjacji CH
3
COOH zmalał z 4.2 % do
0.18%
pH roztworu pochodzi jednak od
mocnego kwasu!
2
])
log([
01
.
0
]
[
3
3
3
=
−
=
≈
+
+
O
H
pH
dm
mol
O
H

Obliczenia - równowagi w
roztworach
Przyk
Przyk
ł
ł
ad 3 bufory
ad 3 bufory
Oblicz pH 1.00 dm
3
roztworu zawierającego 0.010 mola
CH
3
COOH oraz 0.010 mola CH
3
COONa. Stała K
a
dla
tego kwasu w temperaturze 25
o
C wynosi 1.8·10
-5
.
CH
3
COOH,
CH
3
COONa
−
+
−
+
−
+
→
⋅
=
+
↔
+
COO
CH
Na
COONa
CH
K
O
H
COO
CH
O
H
COOH
CH
a
3
3
5
3
3
2
3
10
8
.
1
]
[
]
][
[
3
3
3
COOH
CH
O
H
COO
CH
K
a
+
−
=

Obliczenia - równowagi w
roztworach
Stan początkowy
0.01
0.01
0
Zmiana
-x
+x
+x
Równowaga
0.01-x
0.01+x x
(
)
5
5
10
8
.
1
01
.
0
01
.
0
01
.
0
01
.
0
10
8
.
1
01
.
0
01
.
0
−
−
⋅
=
≅
+
≅
−
⋅
=
−
+
=
x
x
i
x
x
x
x
K
a
+
−
+
↔
+
O
H
COO
CH
O
H
COOH
CH
3
3
2
3
Przyk
Przyk
ł
ł
ad 3 bufory
ad 3 bufory

74
.
4
])
log([
10
8
.
1
]
[
3
3
5
3
=
−
=
⋅
=
=
+
−
+
O
H
pH
dm
mol
O
H
x
Obliczenia - równowagi w
roztworach
Przyk
Przyk
ł
ł
ad 3 bufory
ad 3 bufory
W ogólności
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
−
=
=
=
−
−
+
−
+
+
−
0
3
0
3
0
3
0
3
3
0
3
0
3
3
3
3
3
]
[
]
[
log
log
]
[
]
[
log
])
log([
]
[
]
[
]
[
]
[
]
][
[
COO
CH
COOH
CH
K
COO
CH
COOH
CH
K
O
H
pH
COO
CH
COOH
CH
K
O
H
COOH
CH
O
H
COO
CH
K
a
a
a
a

Bufory
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
s
kw
a
c
c
pK
pH
log
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
=
zas
s
b
w
c
c
pK
pK
pH
log
kwasowy
zasadowy
Własności roztworu buforowego:
- pH nie zmienia się z rozcieńczeniem
- pH zmienia się nieznacznie pod wpływem niewielkiego dodatku
kwasu lub zasady nieznacznie zmienia pH

Obliczenia - równowagi w
roztworach buforowych
Przyk
Przyk
ł
ł
ad 4 dzia
ad 4 dzia
ł
ł
anie buforu
anie buforu
Dodajemy 0.0050 mola NaOH (stałego) do roztworu z
przykładu 3.
CH
3
COOH, CH
3
COONa, NaOH
−
−
+
−
−
+
−
−
−
+
⋅
=
+
↔
+
+
→
+
↔
+
+
→
5
3
3
2
3
3
3
2
3
3
10
8
.
1
a
K
O
H
COO
CH
O
H
COOH
CH
COO
CH
Na
COONa
CH
O
H
COO
CH
COOH
CH
OH
OH
Na
NaOH
]
[
]
][
[
3
3
3
COOH
CH
O
H
COO
CH
K
a
+
−
=
Film 1 bufor działanie.MOV

Obliczenia - równowagi w
roztworach buforowych
Stan początkowy
0.005
0.015
0
Zmiana
-x
+x
+x
Równowaga
0.005-x
0.015+x +x
(
)
5
5
5
10
8
.
1
3
10
8
.
1
005
.
0
015
.
0
015
.
0
015
.
0
005
.
0
005
.
0
10
8
.
1
005
.
0
015
.
0
−
−
−
⋅
=
⋅
=
=
≅
+
≅
−
⋅
=
−
+
=
x
x
K
x
i
x
x
x
x
K
a
a
+
−
+
↔
+
O
H
COO
CH
O
H
COOH
CH
3
3
2
3
Przyk
Przyk
ł
ł
ad 4
ad 4

48
.
0
74
.
4
22
.
5
22
.
5
])
log([
10
0
.
6
]
[
3
3
6
3
=
−
=
∆
=
−
=
⋅
=
=
+
−
+
pH
O
H
pH
dm
mol
O
H
x
Obliczenia - równowagi w
roztworach buforowych
Przyk
Przyk
ł
ł
ad 4
ad 4
Po dodaniu 0.005 mola NaOH do 1 dm
3
czystej wody (pH=7 w
temperaturze 25
o
C)
70
.
4
0
.
7
7
.
11
7
.
11
30
.
2
])
log([
0050
.
0
]
[
3
=
−
=
∆
=
=
−
=
=
−
−
pH
pH
OH
pOH
dm
mol
OH

Bufory
Przyk
Przyk
ł
ł
ad 5 projektowanie roztwor
ad 5 projektowanie roztwor
ó
ó
w buforowych
w buforowych
Potrzebny jest bufor o pH 4.30. Do dyspozycji są następujące kwasy i ich
sole sodowe:
Kwas chlorooctowy CH
2
ClCOOH
K
a
= 1.35·10
-3
Kwas propionowy C
2
H
5
COOH
K
a
= 1.3·10
-5
Kwas benzoesowy C
6
H
5
COOH
K
a
= 6.4·10
-5
Kwas chlorowy (I) HClO
K
a
= 3.5·10
-8
]
[
]
[
]
[
]
[
]
][
[
3
3
3
2
−
+
−
+
−
+
=
=
+
⇔
+
A
HA
K
O
H
HA
A
O
H
K
A
O
H
O
H
HA
a
a

Bufory
1.4·10
3
5.0·10
-5
=3.5·10
-8
Kwas chlorowy
(I)
0.78
5.0·10
-5
=6.4·10
-5
Kwas
benzoesowy
3.8
5.0·10
-5
=1.3·10
-5
Kwas
propionowy
3.7·10
-2
5.0·10
-5
=1.35·10
-3
Kwas
chlorooctowy
Odczynnik
]
[
]
[
−
A
HA
]
[
]
[
−
A
HA
]
[
]
[
−
A
HA
]
[
]
[
−
A
HA
]
[
]
[
−
A
HA
]
[
]
[
]
[
3
−
+
=
A
HA
K
O
H
a
Przyk
Przyk
ł
ł
ad 5 projektowanie roztwor
ad 5 projektowanie roztwor
ó
ó
w buforowych
w buforowych

Bufory
1.4·10
3
5.0·10
-5
=3.5·10
-8
Kwas chlorowy
(I)
0.78
5.0·10
-5
=6.4·10
-5
Kwas
benzoesowy
3.8
5.0·10
-5
=1.3·10
-5
Kwas
propionowy
3.7·10
-2
5.0·10
-5
=1.35·10
-3
Kwas
chlorooctowy
Odczynnik
]
[
]
[
−
A
HA
]
[
]
[
−
A
HA
]
[
]
[
−
A
HA
]
[
]
[
−
A
HA
]
[
]
[
−
A
HA
]
[
]
[
]
[
3
−
+
=
A
HA
K
O
H
a
Przyk
Przyk
ł
ł
ad 5 projektowanie roztwor
ad 5 projektowanie roztwor
ó
ó
w buforowych
w buforowych

Bufory
Przyk
Przyk
ł
ł
ad 6 pojemno
ad 6 pojemno
ść
ść
buforowa
buforowa
Dodajemy 0.0050 mola NaOH (stałego) do 1.00 dm
3
roztworu roztworu zawierającego 0.50 mola CH
3
COOH
oraz 0.50 mola CH
3
COONa. Stała K
a
dla tego kwasu w
temperaturze 25
o
C wynosi 1.8·10
-5
.
CH
3
COOH,
CH
3
COONa, NaOH
−
−
+
−
−
+
−
−
⋅
=
+
↔
+
+
→
+
→
+
5
3
3
2
3
3
3
2
3
3
10
8
.
1
a
K
O
H
COO
CH
O
H
COOH
CH
COO
CH
Na
COONa
CH
O
H
COO
CH
COOH
CH
OH

Bufory
Przyk
Przyk
ł
ł
ad 6 pojemno
ad 6 pojemno
ść
ść
buforowa
buforowa
Stan początkowy
0.495
0.505
0
Zmiana
-x
+x
+x
Równowaga
0.495-x
0.505+x +x
(
)
5
5
10
76
.
1
505
.
0
505
.
0
495
.
0
495
.
0
10
8
.
1
495
.
0
505
.
0
−
−
⋅
=
≅
+
≅
−
⋅
=
−
+
=
x
x
i
x
x
x
x
K
a
+
−
+
↔
+
O
H
COO
CH
O
H
COOH
CH
3
3
2
3

Bufory
Przyk
Przyk
ł
ł
ad 6 pojemno
ad 6 pojemno
ść
ść
buforowa
buforowa
01
.
0
74
.
4
75
.
4
75
.
4
])
log([
10
76
.
1
]
[
3
3
5
3
=
−
=
∆
=
−
=
⋅
=
=
+
−
+
pH
O
H
pH
dm
mol
O
H
x
Zmiana pH w przypadku buforu bardziej rozcieńczonego była znacznie
większa (przykład 4)
Co określa pojemność buforową? Który bufor ma większą pojemność?
48
.
0
74
.
4
22
.
5
=
−
=
∆pH

Iloczyn rozpuszczalności
W nasyconym roztworze słabo rozpuszczalnej soli również
ustala się równowaga:
−
+
+
↔
n
r
m
r
s
m
n
mB
nA
B
A
)
(
)
(
)
(
równowaga heterogeniczna – 2 fazy
m
n
n
m
s
B
A
K
]
[
]
[
−
+
=
iloczyn rozpuszczalności
(solubility product)
)
,
(
p
T
f
K
s
=

Iloczyn rozpuszczalności
R – rozpuszczalność soli, mol/dm
3
m
n
m
n
s
n
m
R
m
n
K
m
R
B
n
R
A
+
−
+
=
⋅
=
⋅
=
]
[
]
[
]
[

Iloczyn rozpuszczalności
Substance
T, °C
K
sp
Carbonates
CaCO
3
25
5 × 10
-9
PbCO
3
20
1.4 × 10
-13
Li
2
CO
3
0
2 × 10
-3
NiCO
3
25
1.2 × 10
-7
Chromates
PbCrO
4
25
1.8× 10
-14
Ag
2
CrO
4
25
1.1× 10
-12
SrCrO
4
25
3.5× 10
-5
Halides: chlorides,
bromides, iodides
CuI
18
7 × 10
-13
PbBr
2
20
9 × 10
-6
PbCl
2
20
1.2 × 10
-5
HgI
2
25
3 × 10
-29
Hg
2
Br
2
25
6 × 10
-23
Hg
2
Cl
2
25
1.4 × 10
-18
AgBr
100
5 × 10
-10
AgCl
10
4 × 10
-11
AgI
25
9 × 10
-17
Hydroxides
Ca(OH)
2
0
9 × 10
-6
Fe(OH)
2
18
7 × 10
-16
Pb(OH)
2
20
2 × 10
-15
Mn(OH)
2
18
1.7 × 10
-13
Oxalates
CdC
2
O
4
25
1.5× 10
-8
MgC
2
O
4
25
8.5× 10
-5
Sulfates
BaSO
4
25
1.1 × 10
-10
CaSO
4
30
6 × 10
-5
Hg
2
SO
4
25
7 × 10
-7
Ag
2
SO
4
0
5 × 10
-6
SrSO
4
0
4 × 10
-7
Sulfides
CdS
18
4 × 10
-30
MnS
18
3 × 10
-14
HgS
18
1.5 × 10
-53
CuS
18
2 × 10
-37

Obliczenia związane z iloczynem
rozpuszczalności
Przyk
Przyk
ł
ł
ad 6 rozpuszczalno
ad 6 rozpuszczalno
ść
ść
Iloczyn rozpuszczalności Cu(IO
3
)
2
=1.4·10
-7
(w temp.
25
o
C)
.
Oblicz rozpuszczalność tego związku w mol/dm
3
.
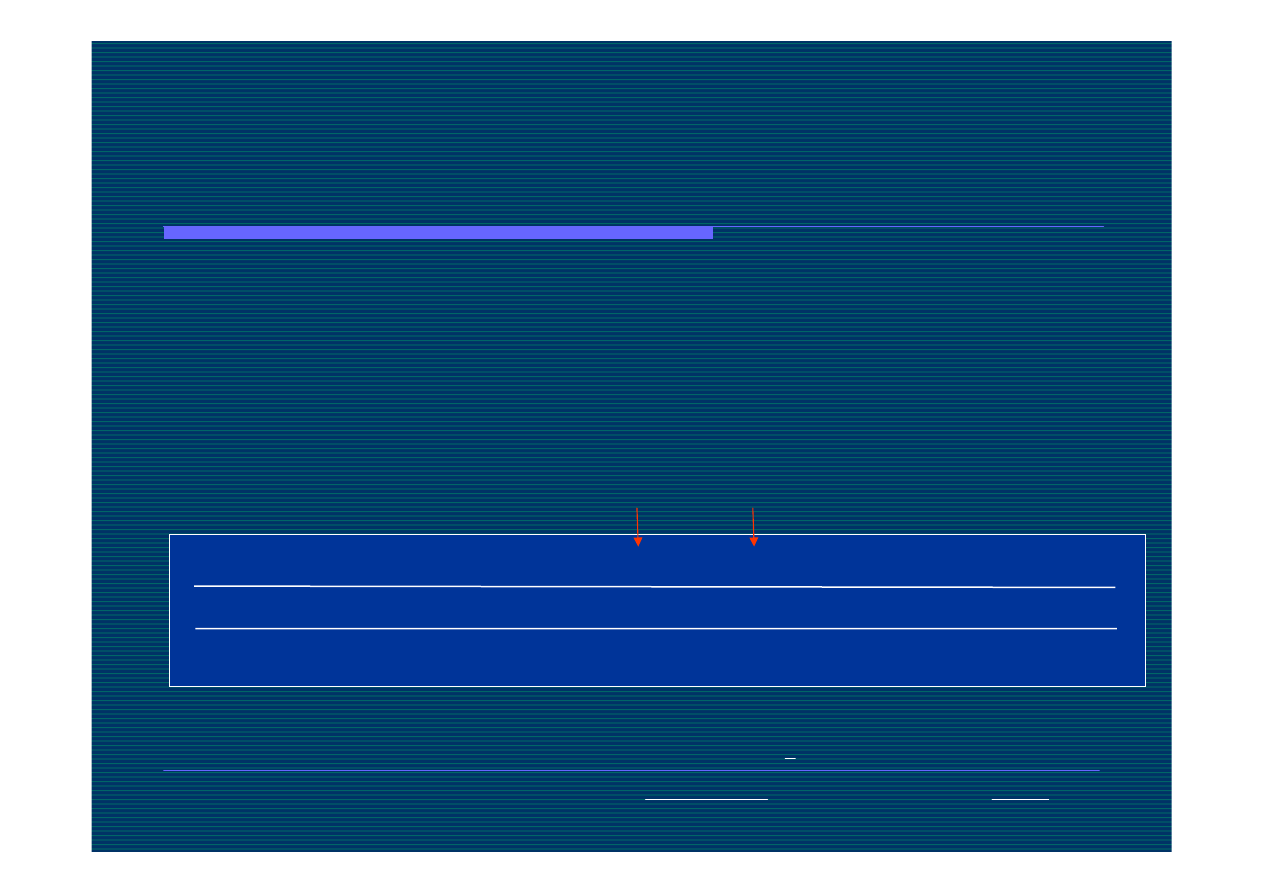
3
3
3
7
7
3
2
)
(
3
3
3
)
(
3
)
(
)
(
2
3
10
3
.
3
4
10
4
.
1
10
4
.
1
4
)
2
(
2
2
)
(
2
3
2
dm
mol
R
R
R
R
K
dm
mol
R
dm
mol
R
dm
mol
R
IO
Cu
IO
Cu
IO
Cu
r
r
s
−
−
−
−
⋅
=
⋅
=
⋅
=
=
⋅
=
+
↔
+
Obliczenia związane z iloczynem
rozpuszczalności
Przyk
Przyk
ł
ł
ad 7 wsp
ad 7 wsp
ó
ó
lny jon i rozpuszczalno
lny jon i rozpuszczalno
ść
ść
Iloczyn rozpuszczalności CaF
2
=4.0·10
-11
(w temp. 25
o
C)
.
Oblicz rozpuszczalność tego związku w wodzie i w
0.025 M roztworze NaF.
2
2
)
(
2
)
(
2
]
][
[
2
2
)
(
−
+
−
+
=
+
↔
F
Ca
K
F
Ca
CaF
CaF
r
s
r
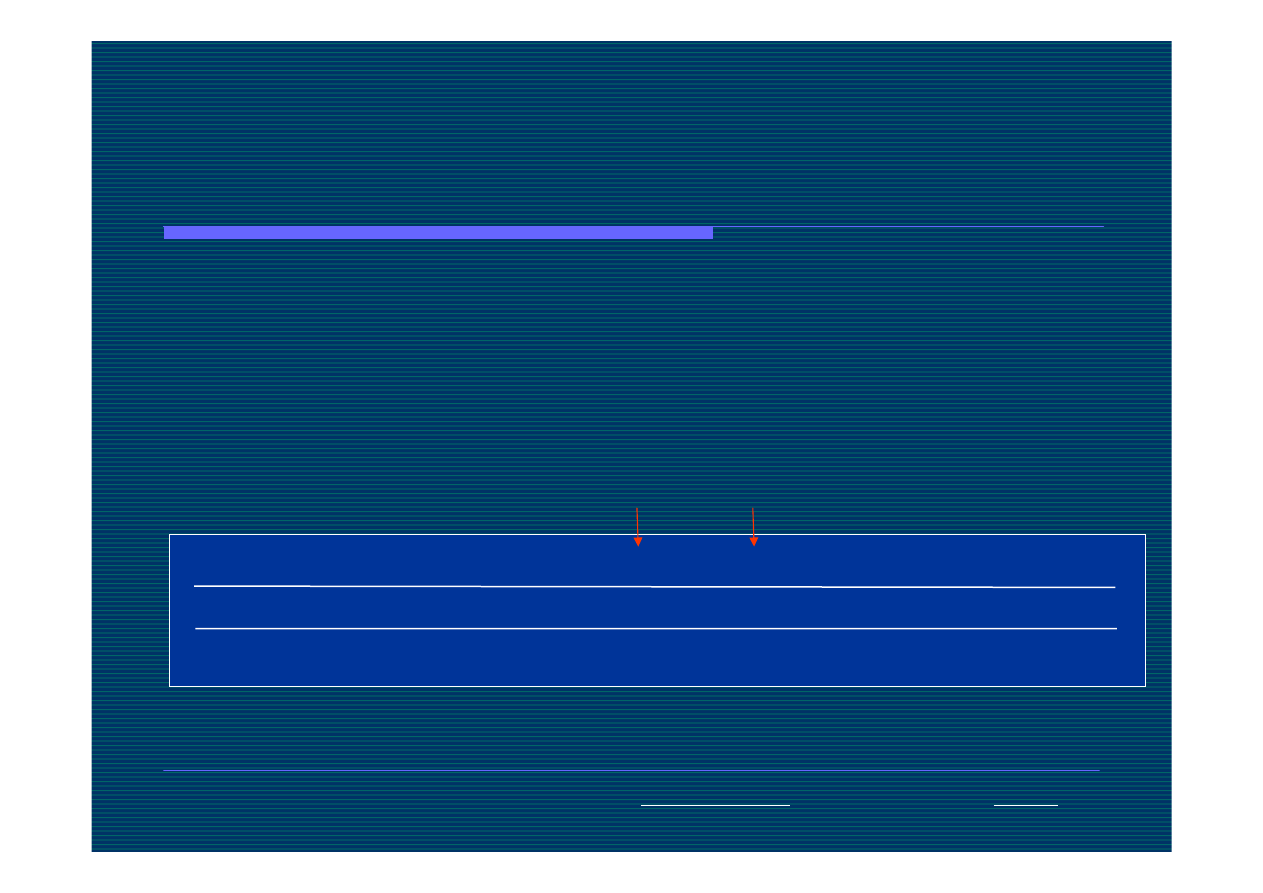
3
4
3
1
11
3
2
10
15
.
2
4
10
0
.
4
4
)
2
(
2
dm
mol
R
R
R
R
K
CaF
−
−
⋅
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
=
≅
⋅
=
Stan początkowy
0
0
Zmiana
+R +2R
Równowaga
R 0+2R
w wodzie
Obliczenia związane z iloczynem
rozpuszczalności
Przyk
Przyk
ł
ł
ad 7 wsp
ad 7 wsp
ó
ó
lny jon i rozpuszczalno
lny jon i rozpuszczalno
ść
ść
Iloczyn rozpuszczalności CaF
2
=4.0·10
-11
(w temp. 25
o
C)
.
Oblicz rozpuszczalność tego związku w wodzie i w
0.025 M roztworze NaF.
2
2
)
(
2
)
(
2
]
][
[
2
2
)
(
−
+
−
+
=
+
↔
F
Ca
K
F
Ca
CaF
CaF
r
s
r
3
6
4
11
2
2
10
4
.
6
10
25
.
6
10
0
.
4
025
.
0
)
2
025
.
0
(
2
dm
mol
R
R
R
R
K
CaF
−
−
−
⋅
=
⋅
⋅
=
⋅
≅
+
⋅
=
Stan początkowy
0
0.025
Zmiana
+R +2R
Równowaga
R 0.025+2R
w NaF

Obliczenia związane z iloczynem
rozpuszczalności
Przyk
Przyk
ł
ł
ad 8 warunki wytr
ad 8 warunki wytr
ą
ą
cania osad
cania osad
ó
ó
w
w
Zmieszano 750 cm
3
0.0040 M roztworu Ce(NO
3
)
3
i
300 cm
3
0.020 M roztworu KIO
3
. Czy wytrąci się osad?
10
)
(
3
3
)
(
3
3
)
(
10
9
.
1
)
(
3
−
−
+
⋅
=
↔
+
s
s
r
r
K
IO
Ce
IO
Ce
Objętość końcowa roztworu:
Z bilansu masy (liczby moli) wynika:
3
,
)
(
,
1050
300
750
3
3
3
cm
V
V
V
KIO
p
NO
Ce
p
k
=
+
=
+
=
3
3
3
3
3
3
3
3
3
3
3
3
3
3
,
,
,
,
,
,
)
(
,
,
)
(
,
,
,
,
KIO
k
IO
k
KIO
p
IO
p
IO
k
IO
p
NO
Ce
k
Ce
k
NO
Ce
p
Ce
p
Ce
k
Ce
p
V
c
V
c
n
n
V
c
V
c
n
n
⋅
=
⋅
=
⋅
=
⋅
=
−
−
−
−
+
+
+
+
⇒
⇒

Obliczenia związane z iloczynem
rozpuszczalności
Przyk
Przyk
ł
ł
ad 8 warunki wytr
ad 8 warunki wytr
ą
ą
cania osad
cania osad
ó
ó
w
w
3
3
3
3
3
2
3
3
3
3
3
3
3
3
10
71
.
5
1050
300
10
0
.
2
]
[
10
86
.
2
1050
750
10
0
.
4
]
[
dm
mol
cm
cm
dm
mol
IO
dm
mol
cm
cm
dm
mol
Ce
−
−
−
−
−
+
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
=
Obliczamy równoważnik reakcji Q
(
) (
)
10
10
3
3
3
3
0
3
0
3
10
9
.
1
10
54
.
3
10
71
.
5
10
90
.
1
]
[
]
[
−
−
−
−
−
+
⋅
=
>
⋅
=
⋅
⋅
⋅
=
⋅
=
s
K
Q
IO
Ce
Q
Osad wytrąci się

Obliczenia związane z iloczynem
rozpuszczalności
Przyk
Przyk
ł
ł
ad 9 warunki wytr
ad 9 warunki wytr
ą
ą
cania osad
cania osad
ó
ó
w
w
Zmieszano 100 cm
3
0.050 M roztworu Pb(NO
3
)
2
i
200 cm
3
0.100 M roztworu NaI. Oblicz stężenia
równowagowe jonów w tym roztworze?
Objętość końcowa roztworu:
Z bilansu masy (liczby moli) wynika:
3
,
)
(
,
300
200
100
2
3
cm
V
V
V
NaI
p
NO
Pb
p
k
=
+
=
+
=
NaI
k
I
k
NaI
p
I
p
I
k
I
p
NO
Pb
k
Pb
k
NO
Pb
p
Pb
p
Pb
k
Pb
p
V
c
V
c
n
n
V
c
V
c
n
n
,
,
,
,
,
,
)
(
,
,
)
(
,
,
,
,
2
3
2
2
3
2
2
2
⋅
=
⋅
=
⋅
=
⋅
=
−
−
−
−
+
+
+
+
8
)
(
2
)
(
2
)
(
10
4
.
1
2
−
−
+
⋅
=
↔
+
s
s
r
r
K
PbI
I
Pb

Obliczenia związane z iloczynem
rozpuszczalności
3
2
3
3
3
1
3
2
3
3
3
2
2
10
67
.
6
300
200
10
0
.
1
]
[
10
67
.
1
300
100
10
0
.
5
]
[
dm
mol
cm
cm
dm
mol
I
dm
mol
cm
cm
dm
mol
Pb
−
−
−
−
−
+
⋅
=
⋅
⋅
=
⋅
=
⋅
⋅
=
1. Obliczamy równoważnik reakcji Q
(
) (
)
8
5
2
2
2
2
0
0
2
10
4
.
1
10
4
.
7
10
67
.
6
10
67
.
1
]
[
]
[
−
−
−
−
−
+
⋅
=
>
⋅
=
⋅
⋅
⋅
=
⋅
=
s
K
Q
I
Pb
Q
Osad wytrąci się
Przyk
Przyk
ł
ł
ad 9 warunki wytr
ad 9 warunki wytr
ą
ą
cania osad
cania osad
ó
ó
w
w

Obliczenia związane z iloczynem
rozpuszczalności
Przyk
Przyk
ł
ł
ad 9 warunki wytr
ad 9 warunki wytr
ą
ą
cania osad
cania osad
ó
ó
w
w
2. Sprawdzamy, czy któryś z substratów jest w nadmiarze
)
(
2
)
(
2
)
(
2
s
r
r
PbI
I
Pb
→
+
−
+
mol
dm
mol
dm
V
c
n
mol
dm
mol
dm
V
c
n
NaI
p
I
p
I
p
NO
Pb
p
Pb
p
Pb
p
02
.
0
1
.
0
2
.
0
005
.
0
05
.
0
1
.
0
3
3
,
,
,
3
3
)
(
,
,
,
2
3
2
2
=
⋅
=
⋅
=
=
⋅
=
⋅
=
−
−
+
+
Pb
2+
jest substratem limitującym
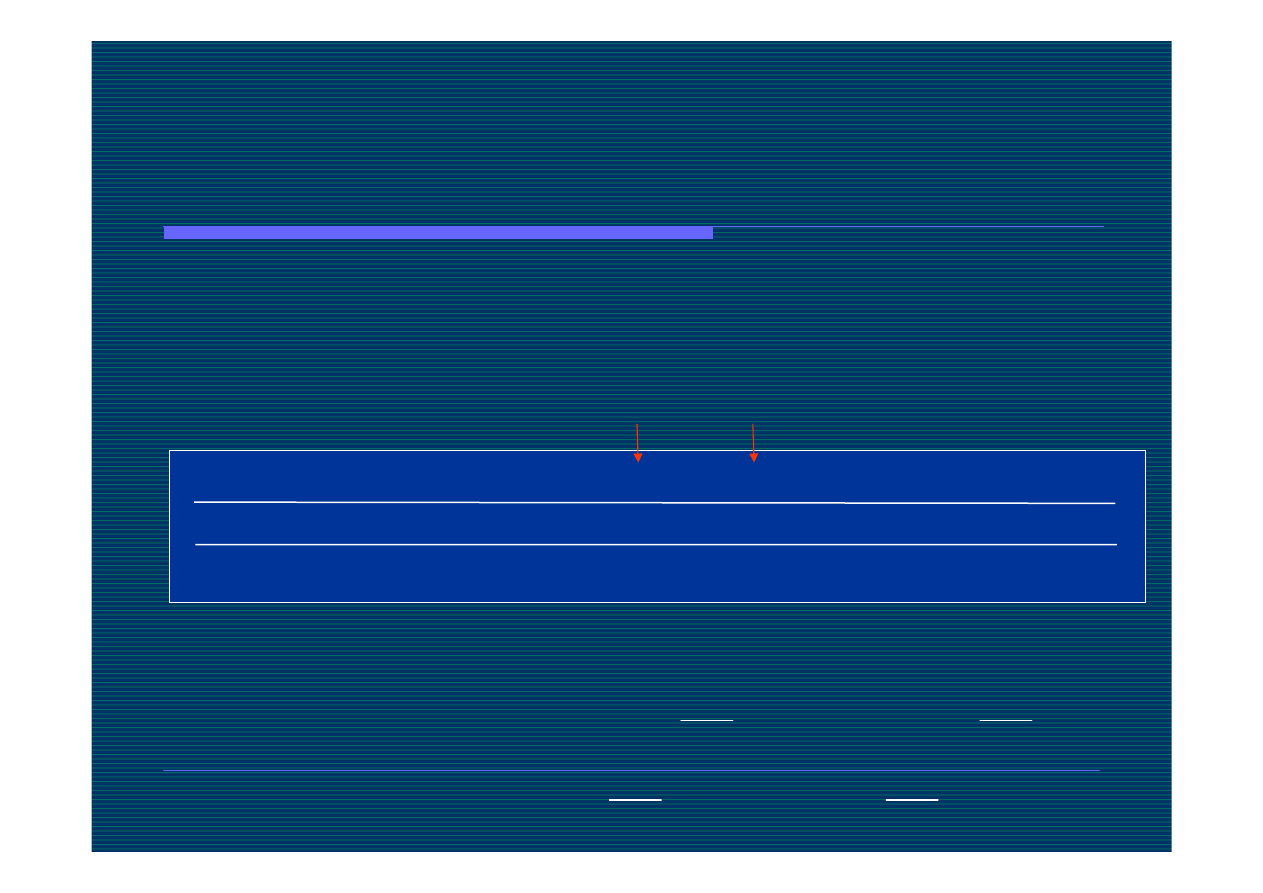
przy założeniu reakcji nieodwracalnej pozostaje w roztworze:
3
2
3
,
,
,
,
10
33
.
3
3
.
0
01
.
0
01
.
0
005
.
0
2
02
.
0
0
0
2
2
dm
mol
dm
mol
c
mol
n
c
n
I
k
I
k
Pb
k
Pb
k
−
⋅
=
=
=
⋅
−
=
=
=
−
−
+
+
Obliczenia związane z iloczynem
rozpuszczalności
Przyk
Przyk
ł
ł
ad 8 warunki wytr
ad 8 warunki wytr
ą
ą
cania osad
cania osad
ó
ó
w
w
3. Obliczamy stężenia równowagowe reakcji
−
+
+
↔
)
(
2
)
(
)
(
2
2
r
r
s
I
Pb
PbI
Stan początkowy
0
0.0333
Zmiana
+x +2x
Równowaga
x 0.0333+2x
3
5
3
2
3
2
3
5
2
2
2
10
3
.
1
2
10
3
.
3
]
[
10
3
.
3
]
[
10
3
.
1
]
[
0333
.
0
0333
.
0
)
2
0333
.
0
(
2
dm
mol
x
dm
mol
I
dm
mol
I
i
dm
mol
Pb
x
x
i
x
x
x
K
PbI
−
−
−
−
−
−
+
⋅
⋅
=
>>
⋅
=
⋅
=
⋅
=
=
<<
⋅
≅
+
⋅
=
sprawdzamy
założenie
Film 1 iloczyn rozpuszczalności.MOV
Iloczyn rozpuszczalności

Iloczyn rozpuszczalności
2AgNO
3(r)
+ NaHCO
3(r)
+ NaOH
(r)
→
Ag
2
CO
3(s)
+ 2NaNO
3
+ H
2
O
Ag
2
CO
3(s)
+ 2NaCl
(r)
→ 2
AgCl
(s)
+ Na
2
CO
3(r)
2AgCl
(s)
+ 2NH
3(r)
→ Ag(NH
3
)
2
Cl
(r)
Ag(NH
3
)
2
Cl
(r)
+ NaBr
(r)
→
AgBr
(s)
+ NaCl + 2 NH
3(r)
AgBr
(s)
+ 2Na
2
S
2
O
3(r)
→ Na
3
Ag(S
2
O
3
)
2(r)
+ NaBr
(r)
Na
3
Ag(S
2
O
3
)
2(r)
+ KI →
AgI
(s)
+ KNaS
2
O
3(r)
+ Na
2
S
2
O
3(r)
2AgI
(s)
+ Na
2
S
(r)
→
Ag
2
S
(s)
+ 2NaI
(r)
brązowy osad
biały osad
rozpuszczanie
rozpuszczanie
biały osad
kremowy osad
brunatny osad

Iloczyn rozpuszczalności
S
Ag
AgI
AgBr
AgCl
CO
Ag
R
R
R
R
R
2
3
2
>
>
>
>
17
3
49
3
2
2
8
16
2
7
13
2
5
10
2
4
3
12
3
2
3
2
10
4
.
3
4
10
6
.
1
4
]
[
]
[
10
2
.
1
10
5
.
1
]
][
[
10
1
.
7
10
0
.
5
]
][
[
10
3
.
1
10
6
.
1
]
][
[
10
3
.
1
4
10
2
.
8
4
]
[
]
[
2
3
2
−
−
−
+
−
−
−
+
−
−
−
+
−
−
−
+
−
−
−
+
⋅
=
⋅
=
=
=
⋅
=
⋅
=
=
=
⋅
=
⋅
=
=
=
⋅
=
⋅
=
=
=
⋅
=
⋅
=
=
=
R
R
S
Ag
K
R
R
I
Ag
K
R
R
Br
Ag
K
R
R
Cl
Ag
K
R
R
CO
Ag
K
S
Ag
AgI
AgBr
AgCl
CO
Ag
Ag
2
CO
3
K=8.1·10
-12
AgCl
K=1.6·10
-10
AgBr
K=5.0 ·10
-13
AgI
K=1.5·10
-16
Ag
2
S
K=1.6·10
-49
Obserwacja
Wyjaśnienie
3
dm
mol
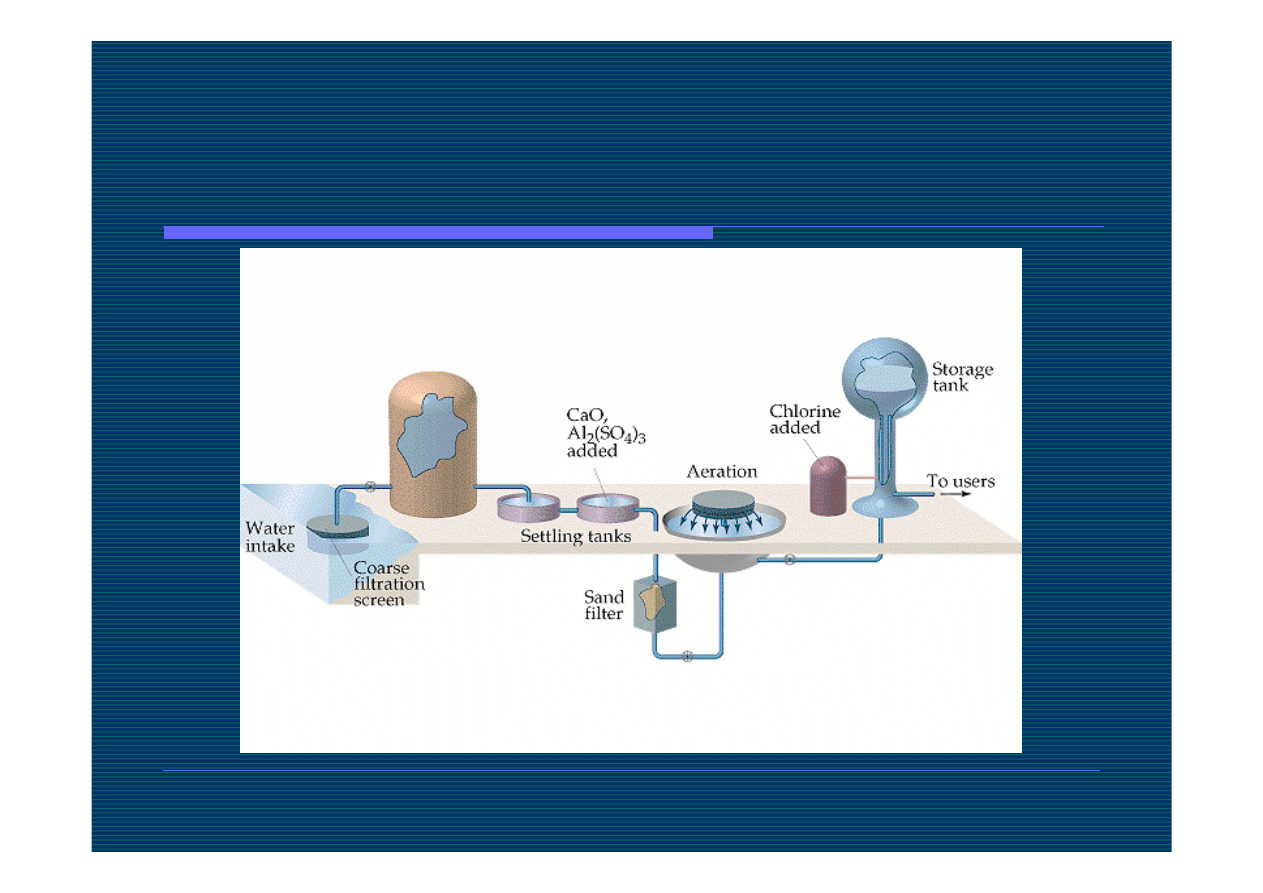
Filtrowanie wody
Wyszukiwarka
Podobne podstrony:
Fizjologia Cwiczenia 11 id 1743 Nieznany
Biologia Cwiczenia 11 id 87709 Nieznany (2)
dodatkowe1 analiza 11 12 2 sem Nieznany
moje wykresy 11 id 306777 Nieznany
11 21id 12110 Nieznany (2)
G2 PB 02 B Rys 3 11 id 185401 Nieznany
III CZP 33 11 id 210275 Nieznany
11 14id 12096 Nieznany (2)
2013 11 04id 28244 Nieznany (2)
mat bud cwicz 10 11 id 282450 Nieznany
Odpowiedzi 1 3 5 8 9 11 13 id 3 Nieznany
grupa 11 id 441853 Nieznany
24 11 id 30514 Nieznany (2)
mnozenie do 25 11 id 304283 Nieznany
cwiczenie 11 id 125145 Nieznany
11 transportid 12256 Nieznany (2)
11 bucid 12376 Nieznany (2)
Egzamin Zobowiazania (11 18) id Nieznany
więcej podobnych podstron