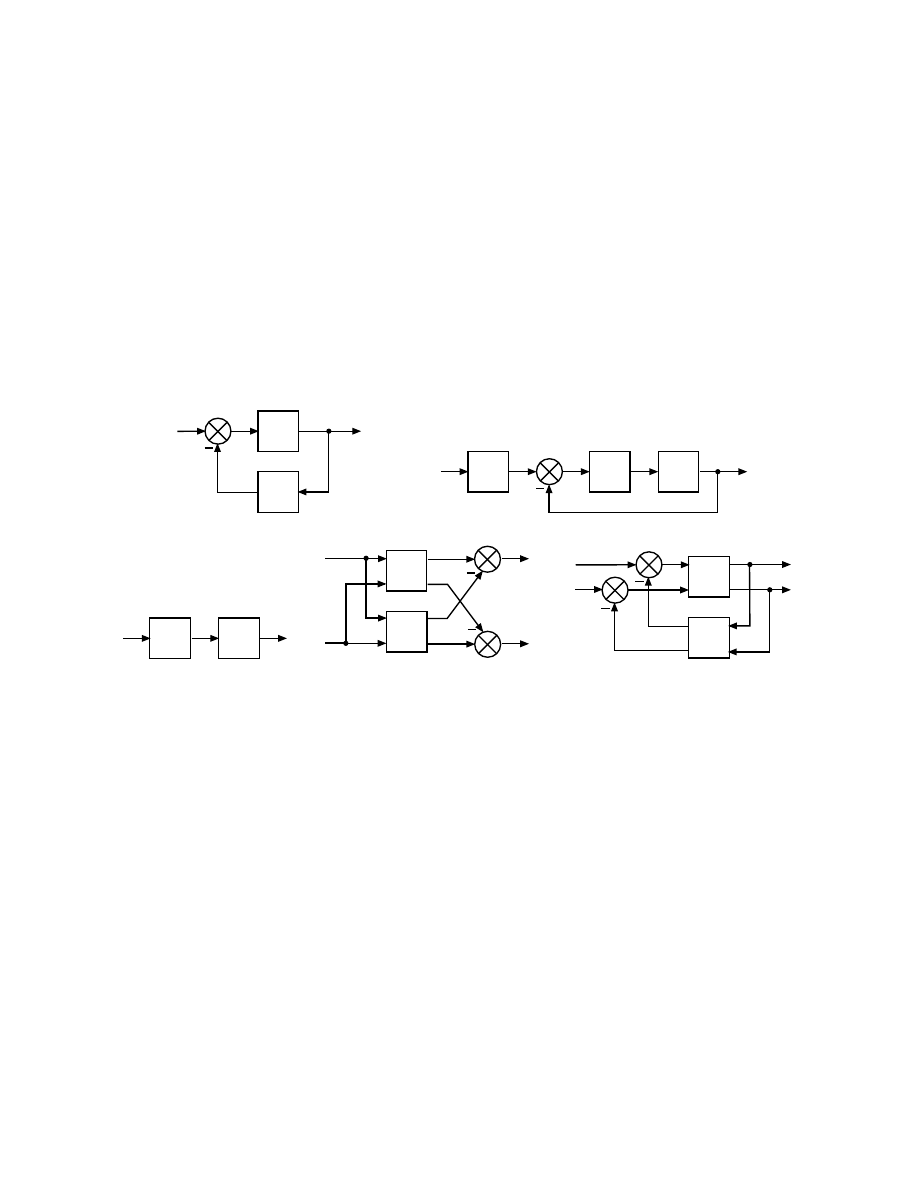
Ćwiczenia z teorii systemów

Lista 1

23 lutego 2010

1. Na podstawie schematów blokowych systemów z rys. 1 wyznaczyć ich opis analityczny w formie równań

algebraicznych lub różniczkowych. Parametry K

1

i K

2

na schemacie blokowym 1(c) są następujące:

2

3

u

y

(a)

3

0,5

R

u

y

(b)

K

2

K

1

y

u

(c)

y

1

y

2

u

1

u

2

K

1

K

2

(d)

u

2

u

1

y

2

y

1

K

1

K

2

(e)

Rys. 1: Schematy blokowe systemów z zadania 1.

K

1

=






3

0

1

4

−1 2






,

K

2

=

"

1

2

−1

0

3

2

#

.

Dla systemu z rys. 1(d)

K

1

=

"

3

−2

1

4

#

,

K

2

=

"

−5 3

0

2

#

.

Schemat blokowy na rys. 1(e) ma parametry:

K

1

=

"

2

1

0

1

#

,

K

2

=

"

−1 0

2

2

#

.

2. Mamy daną halę produkcyjną. Aby stworzyć produkt y

1

potrzebujemy 2 jednostki komponentu u

1

,

4 jednostki komponentu u

2

oraz 3 jednostki komponentu u

3

. Aby stworzyć produkt y

2

potrzebujemy

1

7 jednostek komponentu u

1

, tyle samo komponentu u

2

oraz 5 jednostek komponentu u

3

. Stworzyć

schemat blokowy (wzmocnienia, przecięcia niefunkcyjne, węzły sumacyjne) oraz wyznaczyć funkcje
opisujące zależności między komponentami i produktami. Zapisać te zależność w formie macierzowej.

3. Dane są matematyczne opisy systemów, przy czym u i y oznaczają odpowiednio sygnał wejściowy

i wyjściowy, natomiast a i b są pewnymi parametrami liczbowymi. Które z nich są liniowe? Które są
statyczne, a które dynamiczne? Uzasadnij odpowiedź.

(a) y = au,

(b) y = au + b,

(c) y = 2u

2

,

(d) y

0

(t) = y(t) + u(t)

4. Mamy dany opis y = Au, gdzie A jest macierzą opisującą zbiór wzmocnień dla różnych wejść systemu.

Wyznaczyć funkcje opisujące ten system oraz zbudować schemat blokowy według znanych reguł jego
tworzenia.

A =






6

1

0

3

1

1






5. Dany jest opis systemu dyskretnego w formie równania różnicowego:

y(n) = 0.5y(n − 1) − 0.25u(n − 1),

gdzie n = 1, 2 . . .

Wyznaczyć wartości pierwszych 3 wyrazów ciągu odpowiedzi, przy warunku początkowym y(0) = 0 dla
stałego wymuszenia u(n) = 1. Narysować schemat blokowy tego systemu z wykorzystaniem elementów
opóźniających.

6. Dane są opisy analityczne systemów. Wyznaczyć ich schematy blokowe używając tylko wzmacniaczy,

układów całkujących, sumatorów i węzłów zaczepowych (rozgałęźników).

(a) y

1

= 2u

1

,

y

2

= −0,5u

2

+ 4u

3

(b) y

0

(t) + 2y(t) = 0,25u(t)

(c) y

00

(t) + 4y

0

(t) + y(t) = 5u(t)

Jacek Cichosz

2