1.

Przykłady

1.1.

X

≠≠≠≠

φφφφ

, jedno rozwiązanie optymalne, n = 2

Funkcja celu:

2

1

0

4

max

x

x

x

+

=

Ograniczenia:

0

,

36

5

4

1

4

2

.

3

.

2

.

1

2

1

2

1

2

1

≥











≤

+

≤

+

−

≤

+

−

x

x

x

x

x

x

x

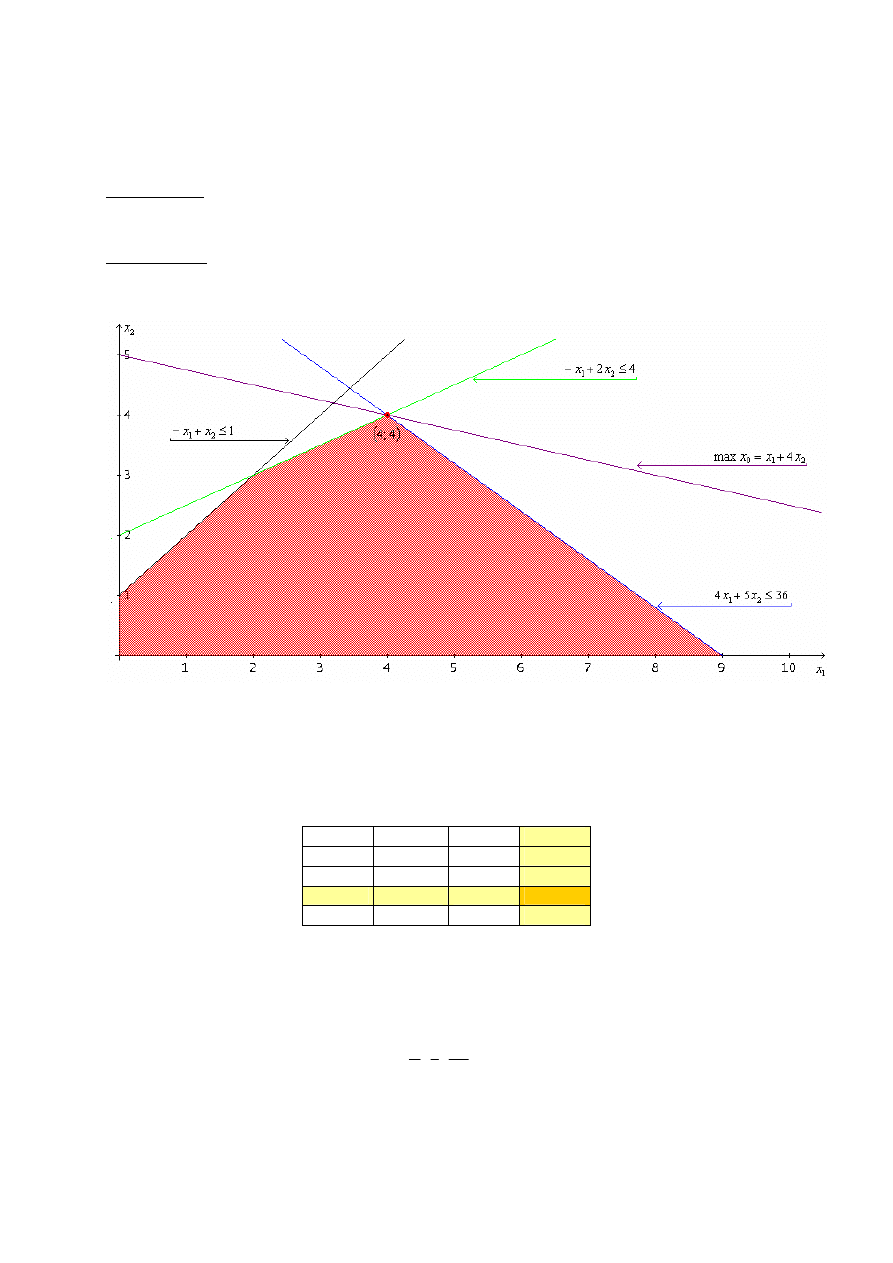
Rys. 1. Ilustracja graficzna do przykładu pierwszego (Derive)

Rozwiązanie z wykorzystaniem tablic simpleks

Na podstawie wyżej przedstawionej funkcji celu i ograniczeniom zbudowano pierwszą
tablicę.

Przykład 1 - Tablica 1

b

x

1

x

2

x

0

0

-1

-4

x

3

4

-1

2

x

4

1

-1

1

x

5

36

4

5

1.

W kolumnie b brak jest elementów ujemnych.

2.

W wierszu x

0

występuje element ujemny – brak rozwiązania optymalnego.

3.

Najmniejsza wartość wiersza x

0

wynosi

{

}

4

4

,

1

,

0

min

−

=

−

−

(kolumna x

2

).

4.

Wyznaczenie punktu centralnego w kolumnie x

2

(rozpatrywane tylko elementy

dodatnie) poprzez obliczenie

{

}

1

2

7

,

1

,

2

min

5

36

,

1

1

,

2

4

min

=

=













.

.

5.

Obliczenie nowych wartości do tablicy 2.

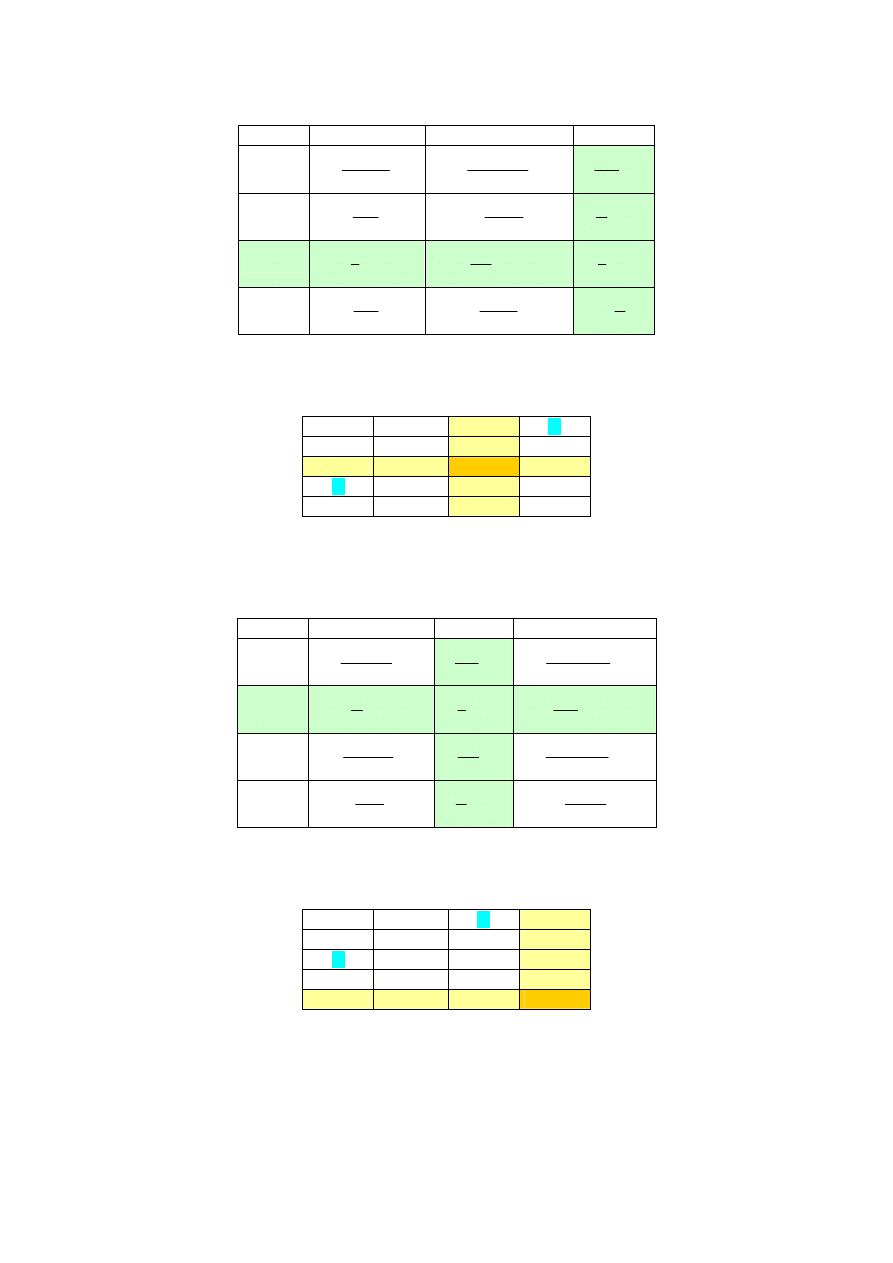
Przykład 1 – Tworzenie tablicy 2

b

x

1

x

2

x

0

4

1

)

4

(

1

0

=

−

⋅

−

5

1

)

4

(

1

1

−

=

−

⋅

−

−

−

4

1

4

=

−

−

x

3

2

1

2

1

4

=

⋅

−

1

1

2

1

1

=

⋅

−

−

−

2

1

2

−

=

−

x

4

1

1

1

=

1

1

1

−

=

−

1

1

1

=

x

5

31

1

5

1

36

=

⋅

−

9

1

5

1

4

=

⋅

−

−

1

5

−

W ten sposób otrzymano tablicę 2.

Przykład 1 - Tablica 2

b

x

1

x

4

x

0

4

-5

4

x

3

2

1

-2

x

2

1

-1

1

x

5

31

9

-5

W nowo utworzonej tablicy w wierszu x

0

nadal znajduje się element ujemny w związku z

czym obliczono kolejną tablicę stosując wcześniej podany algorytm.

Przykład 1 - Tworzenie tablicy 3

b

x

1

x

4

x

0

14

1

)

5

(

2

4

=

−

⋅

−

5

1

5

=

−

−

6

1

)

5

(

2

4

−

=

−

⋅

−

−

x

3

2

1

2

=

1

1

1

=

2

1

2

−

=

−

x

2

3

1

)

1

(

2

1

=

−

⋅

−

1

1

1

=

−

−

1

1

)

1

(

2

1

−

=

−

⋅

−

−

x

5

13

1

9

2

31

=

⋅

−

9

1

9

−

=

−

13

1

9

2

5

=

⋅

−

−

−

W powyższy sposób utworzono tablicę 3.

Przykład 1 - Tablica 3

b

x

3

x

4

x

0

14

5

-6

x

1

2

1

-2

x

2

3

1

-1

x

5

13

-9

13

Ponownie w wierszu x

0

znalazł się element ujemnym w związku z czym rozwiązanie

optymalne nadal nie zostało odnalezione.

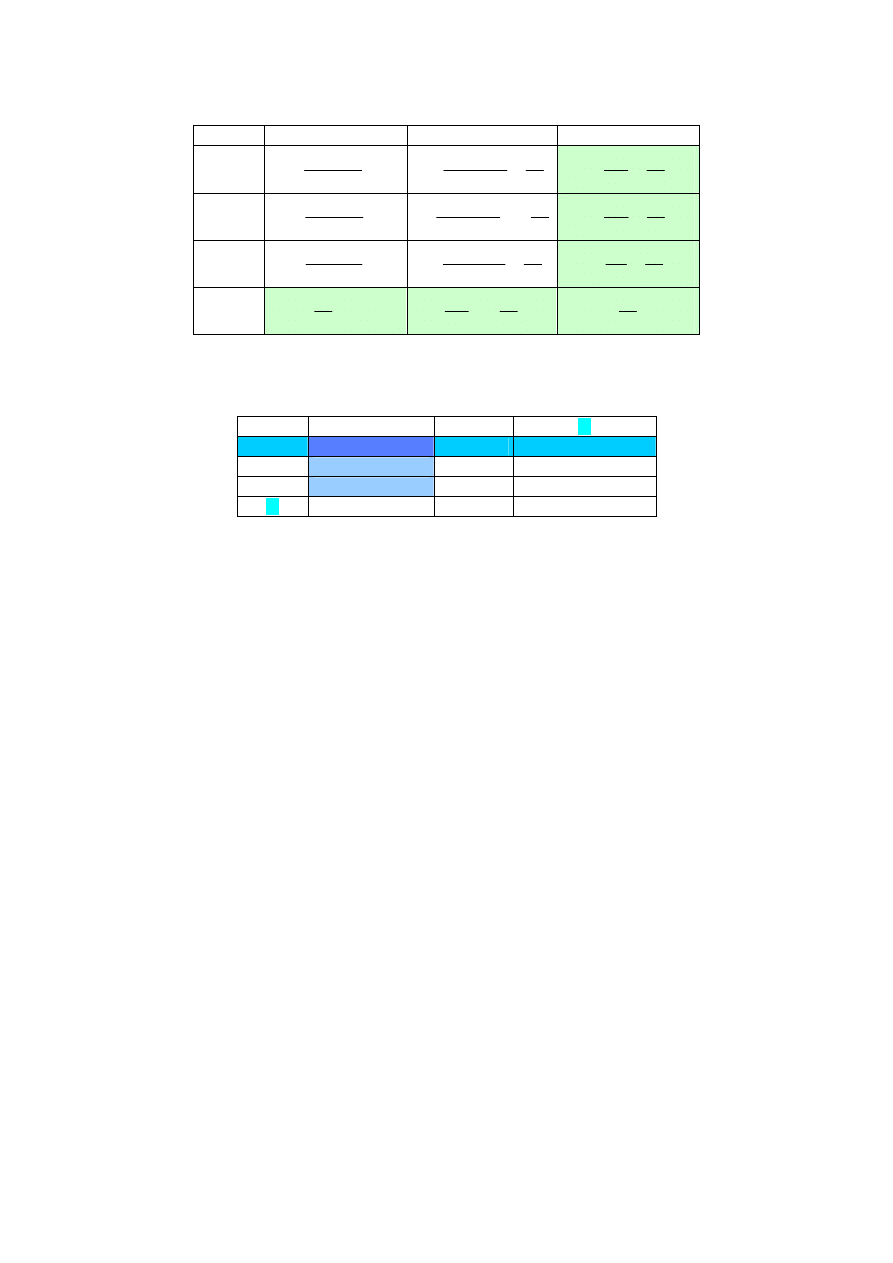
Przykład 1 - Tworzenie tablicy 4

b

x

3

x

4

x

0

20

13

)

6

(

13

14

=

−

⋅

−

13

11

13

)

6

(

9

5

=

−

⋅

−

−

13

6

13

6

=

−

−

x

1

4

13

)

2

(

13

2

=

−

⋅

−

13

5

13

)

2

(

9

1

−

=

−

⋅

−

−

13

2

13

2

=

−

−

x

2

4

13

)

1

(

13

3

=

−

⋅

−

13

4

13

)

1

(

9

1

=

−

⋅

−

−

13

1

13

1

=

−

−

x

5

1

13

13

=

13

9

13

9

−

=

−

13

1

Ostatecznie otrzymano tablicę z rozwiązaniem.

Przykład 1 – Tablica 4

b

x

3

x

5

x

0

20

0.85

0.46

x

1

4

-0.38

0.15

x

2

4

0.31

0.08

x

4

1

-0.69

0.08

W wierszu x

0

brak jest elementów ujemnych w związku z czym tablica 4 zawiera rozwiązanie

optymalne.

x

0

= 20

x

1

= 4

x

2

= 4

Wyniki obliczeń (Matlab)

x

1

= 4

x

2

= 4

fval = 20
iterations = 3
exitflag = 1 (Function converged to a solution x)