Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

1

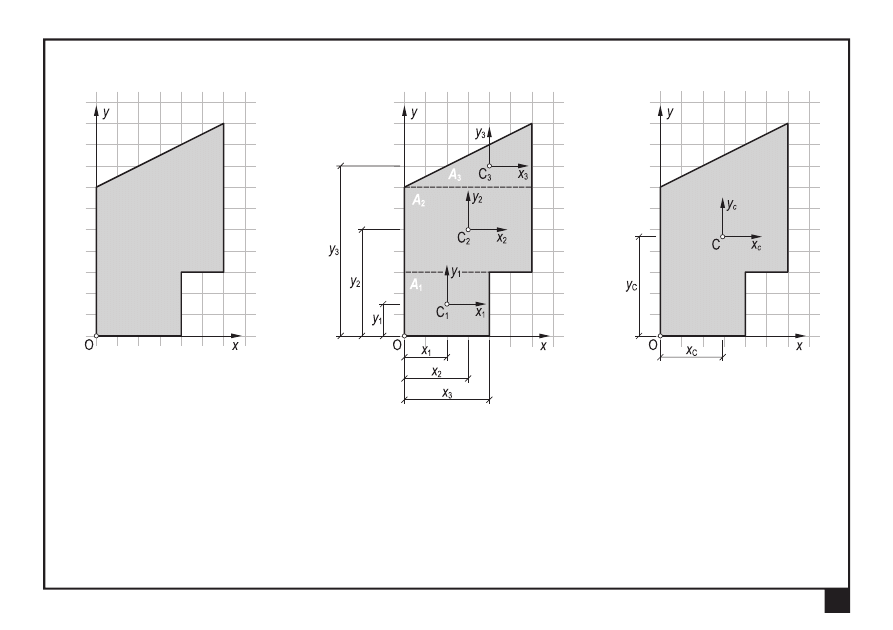
Środek masy figury płaskiej

y

x,

—

układ osi dowolnych

i

i

y

x ,

—

układ osi centralnych i-tej figury regularnej (lokalne osie centralne)

)

,

(

C

i

i

i

y

x

—

środek masy i-tej figury regularnej

i

A

—

pole

powierzchni

i-tej figury regularnej

c

c

y

x ,

—

układ osi centralnych figury złożonej

)

,

(

C

C

C

y

x

—

środek masy figury złożonej

Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

2

Środek masy figury płaskiej

Współrzędne środka masy C (

C

C

,y

x

) figury złożonej:

∑

∑

i

i

i

A

x

A

x =

C

[m]

(1.1)

∑

∑

i

i

i

A

y

A

y =

C

[m]

(1.2)

gdzie:

i

A

—

pole

powierzchni

i-tej figury regularnej,

i

x

—

odległość środka masy i-tej figury regularnej
od osi x dowolnego układu współrzędnych,

i

y

—

odległość środka masy i-tej figury regularnej
od osi y dowolnego układu współrzędnych.

Wielkości

∑

i

i

x

y

A

S =

∫

=

A

A

y d

[m

3

]

(1.3)

∑

i

i

y

x

A

S =

∫

=

A

A

x

d

[m

3

]

(1.4)

nazywamy

momentami statycznymi figury złożonej względem osi

odpowiednio

x oraz y

Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

3

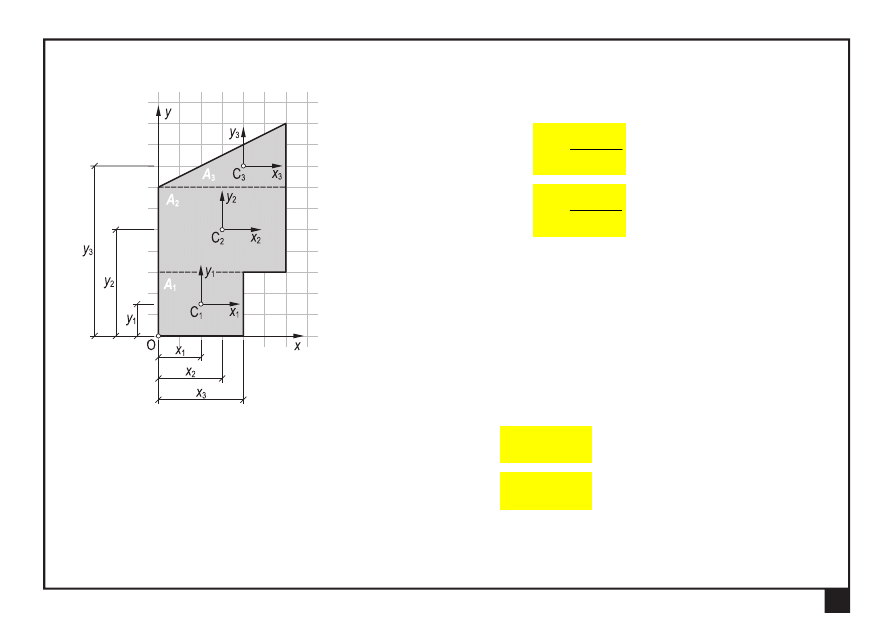
Środek masy figury płaskiej

Wielkość

∑

i

A

A =

∫

=

A

A

d [m

2

]

(1.5)

jest polem powierzchni figury złożonej

Współrzędne środka masy C (

C

C

,y

x

) figury złożonej:

A

S

x

y

=

C

∫

∫

=

A

A

A

A

x

d

d

[m]

(1.6)

A

S

y

x

=

C

∫

∫

=

A

A

A

A

y

d

d

[m]

(1.7)

Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

4

Geometryczne momenty bezwładności figur płaskich

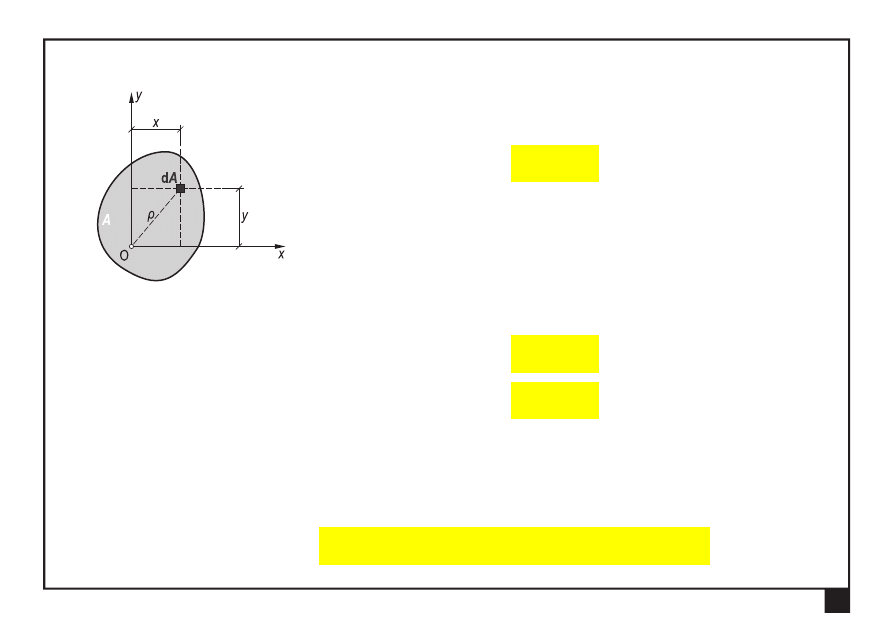
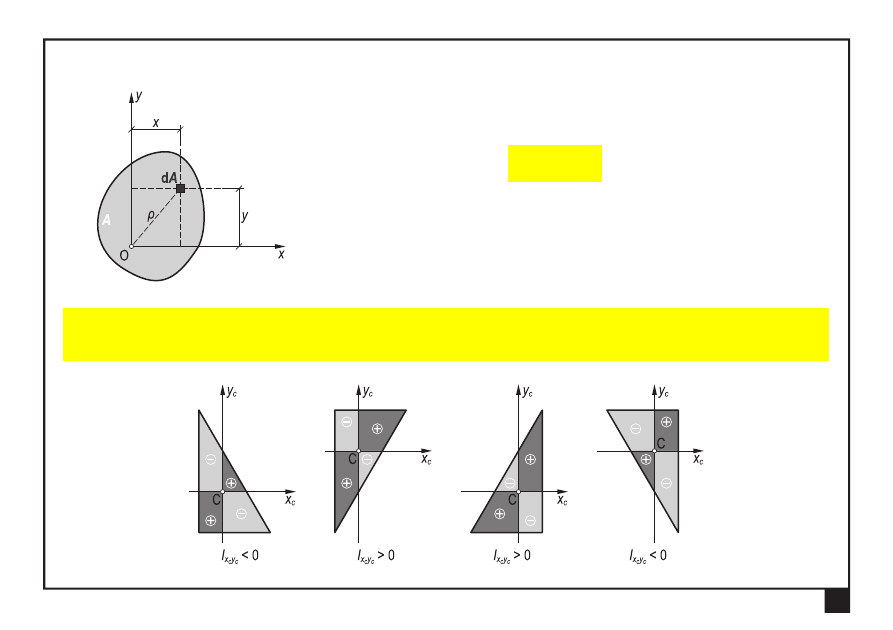
Moment bezwładności

O

I

figury płaskiej względem punktu O

(biegunowy moment bezwładności):

∫

=

A

A

ρ

I

d

2

O

[m

4

]

(1.8)

gdzie:

ρ

—

odległość elementu powierzchni od punktu O,

A

d

— element powierzchni.

Momenty bezwładności

x

I

,

y

I

figury płaskiej względem osi

odpowiednio

x oraz y:

∫

=

A

x

A

y

I

d

2

[m

4

]

(1.9)

∫

=

A

y

A

x

I

d

2

[m

4

]

(1.10)

gdzie:

y

x

,

— odległość elementu powierzchni od osi odpowiednio

y oraz x,

A

d — element powierzchni.

y

x

A

A

A

A

I

I

A

y

A

x

A

y

x

A

ρ

I

+

=

+

=

+

=

=

∫

∫

∫

∫

d

d

d

)

(

d

2

2

2

2

2

O

(1.11)

Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

5

Geometryczne momenty bezwładności figur płaskich

Moment dewiacji (moment zboczenia, moment odśrodkowy)

xy

I

figury płaskiej dla układu współrzędnych Oxy:

∫

=

A

xy

A

xy

I

d

[m

4

]

(1.12)

gdzie:

y

x

,

— odległość elementu powierzchni od osi odpowiednio y oraz x,

A

d

— element powierzchni.

Momenty bezwładności przyjmują tylko wartości dodatnie, natomiast momenty dewiacji

mogą być zarówno dodatnie, jak i ujemne. Znak momentu dewiacji zależy od położenia figury.

Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

6

Geometryczne momenty bezwładności figur płaskich

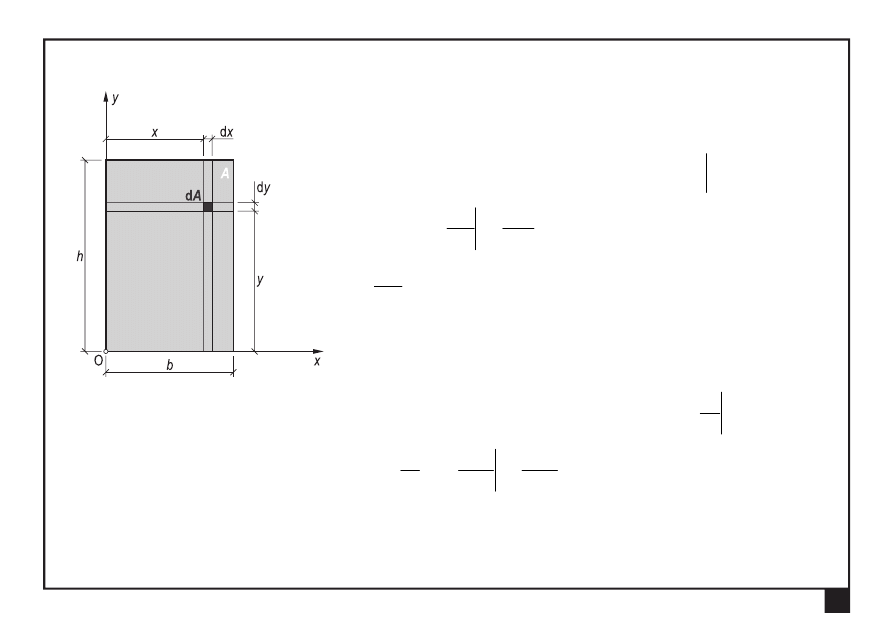
Momenty bezwładności prostokąta o bokach bh względem
osi dowolnych y

x

,

:

3

3

d

d

d

d

d

d

d

3

0

3

0

2

0

0

2

0

0

2

2

2

h

b

b

y

y

b

y

y

x

y

y

x

y

y

x

y

A

y

I

h

h

h

b

h

b

A

x

=

=

=

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

=

∫

∫

∫ ∫

∫ ∫

∫

3

3

h

b

I

y

=

Moment dewiacji prostokąta o bokach bh względem
osi dowolnych

y

x,

:

4

4

d

2

d

2

d

d

d

d

d

2

2

0

2

2

0

2

0

0

2

0

0

h

b

b

y

y

b

y

y

x

y

y

x

xy

y

x

xy

A

xy

I

h

h

h

b

h

b

A

xy

=

=

=

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

=

∫

∫

∫ ∫

∫ ∫

∫

Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

7

Geometryczne momenty bezwładności figur płaskich

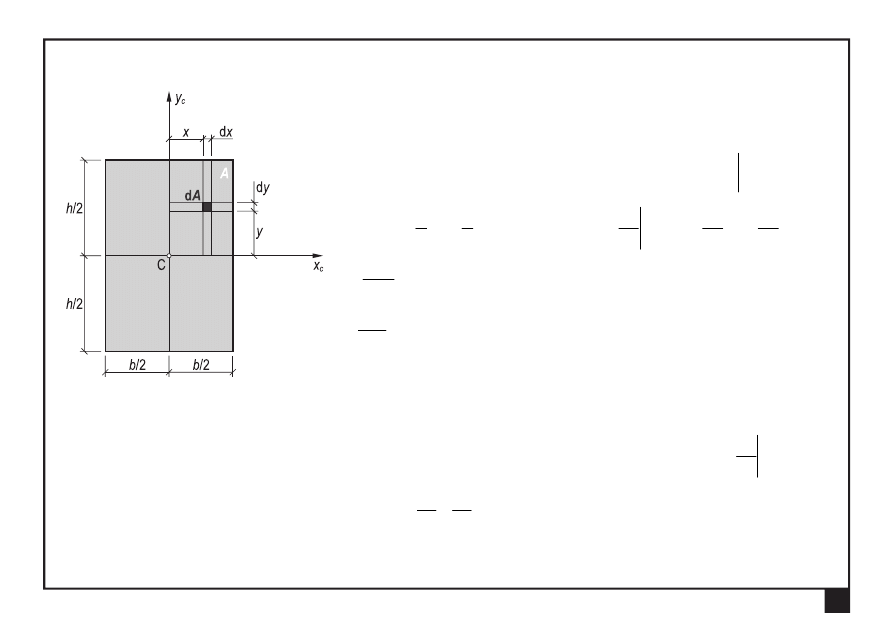
Momenty bezwładności prostokąta o bokach bh względem
osi centralnych

c

c

y

x ,

:

12

24

24

3

d

d

2

2

d

d

d

d

d

d

3

3

3

2

/

2

/

3

2

/

2

/

2

2

/

2

/

2

2

/

2

/

2

/

2

/

2

2

/

2

/

2

/

2

/

2

2

2

h

b

h

h

b

y

b

y

y

b

y

b

b

y

y

x

y

y

x

y

y

x

y

A

y

I

h

h

h

h

h

h

h

h

b

b

h

h

b

b

A

x

c

=

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

=

=

=

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛−

−

=

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

=

+

−

+

−

+

−

+

−

+

−

+

−

+

−

∫

∫

∫

∫ ∫

∫ ∫

∫

12

3

h

b

I

y

=

Moment dewiacji prostokąta o bokach bh względem
osi centralnych

c

c

y

x ,

:

0

d

0

d

8

8

d

2

d

d

d

d

d

2

/

2

/

2

/

2

/

2

2

2

/

2

/

2

/

2

/

2

2

/

2

/

2

/

2

/

=

=

⎥

⎦

⎤

⎢

⎣

⎡

−

=

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

=

∫

∫

∫

∫ ∫

∫ ∫

∫

+

−

+

−

+

−

+

−

+

−

+

−

y

y

b

b

y

y

x

y

y

x

xy

y

x

xy

A

xy

I

h

h

h

h

h

h

b

b

h

h

b

b

A

y

x

c

c

Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

8

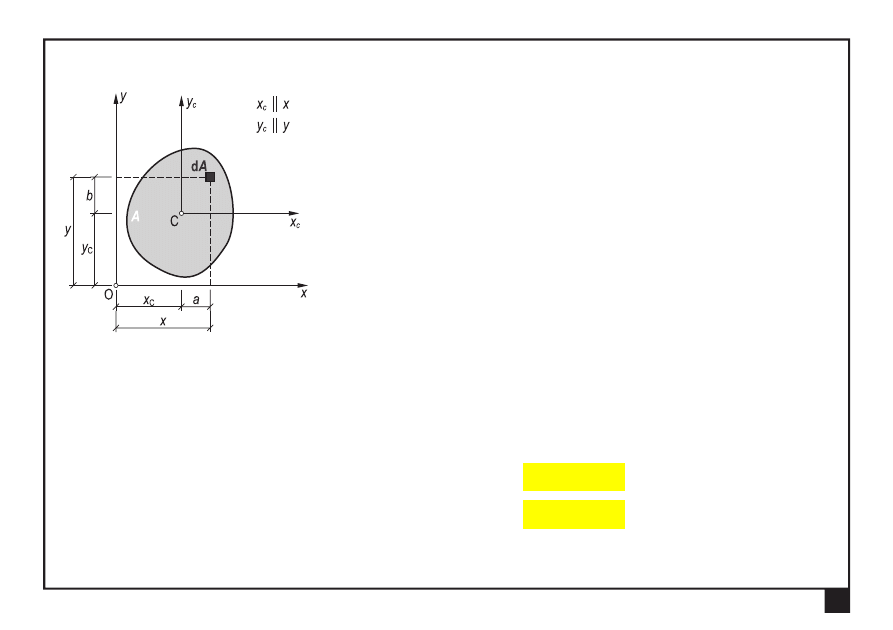
Twierdzenie Steinera

Momenty bezwładności

x

I

,

y

I

oraz moment dewiacji

xy

I

figury płaskiej względem osi dowolnych y

x,

:

∫

=

A

x

A

y

I

d

2

,

∫

=

A

y

A

x

I

d

2

,

∫

=

A

xy

A

xy

I

d

Momenty bezwładności

c

x

I

,

c

y

I

oraz moment dewiacji

c

c

y

x

I

figury płaskiej względem osi centralnych

c

c

y

x

,

(momenty centralne):

∫

=

A

x

A

b

I

c

d

2

,

∫

=

A

y

A

a

I

c

d

2

,

∫

=

A

y

x

A

ab

I

c

c

d

Podstawiamy

a

x

x

+

=

C

,

b

y

y

+

=

C

, przy czym

C

C

,

y

x

— stałe,

b

a

y

x

,

,

,

— zmienne:

2

C

2

C

0

C

2

2

C

d

d

2

d

d

)

(

y

A

I

A

y

A

b

y

A

b

A

y

b

I

c

x

A

A

A

A

x

+

=

+

+

=

+

=

∫

∫

∫

∫

=

43

42

1

2

C

y

A

I

I

c

x

x

+

=

(1.13)

2

C

x

A

I

I

c

y

y

+

=

(1.14)

Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

9

Twierdzenie Steinera

C

C

C

C

0

C

0

C

C

C

d

d

d

d

d

)

)(

(

y

x

A

I

A

y

x

A

b

x

A

a

y

A

ab

A

y

b

x

a

I

c

c

y

x

A

A

A

A

A

xy

+

=

=

+

+

+

=

+

+

=

∫

∫

∫

∫

∫

=

=

43

42

1

43

42

1

C

C

y

x

A

I

I

c

c

y

x

xy

+

=

(1.15)

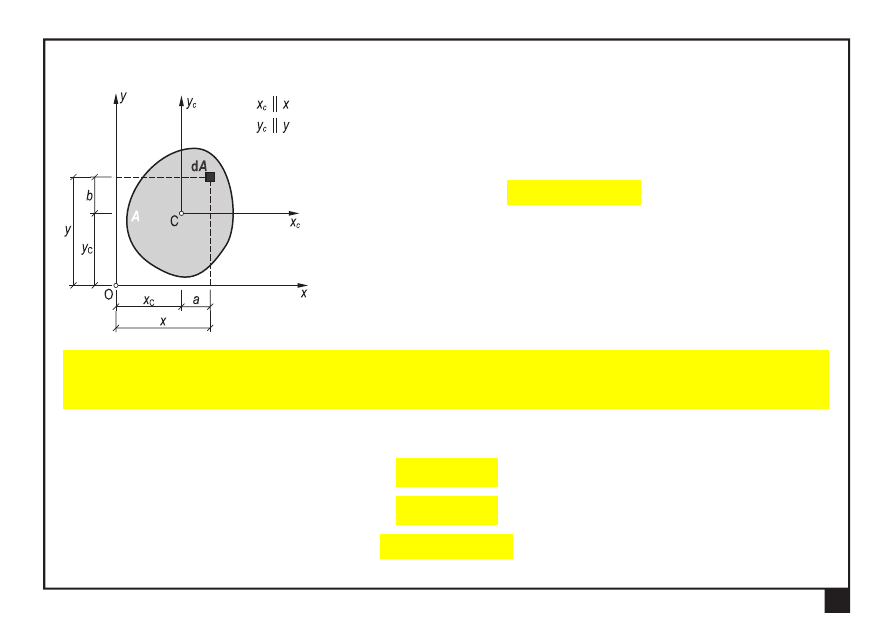
Moment bezwładności figury płaskiej względem dowolnej osi równoległej do osi centralnej

jest równy momentowi centralnemu zwiększonemu o iloczyn powierzchni figury

przez kwadrat odległości między osiami.

Odwrotne twierdzenie Steinera

2

C

y

A

I

I

x

x

c

−

=

(1.16)

2

C

x

A

I

I

y

y

c

−

=

(1.17)

C

C

y

x

A

I

I

xy

y

x

c

c

−

=

(1.18)

Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

10

Twierdzenie Steinera

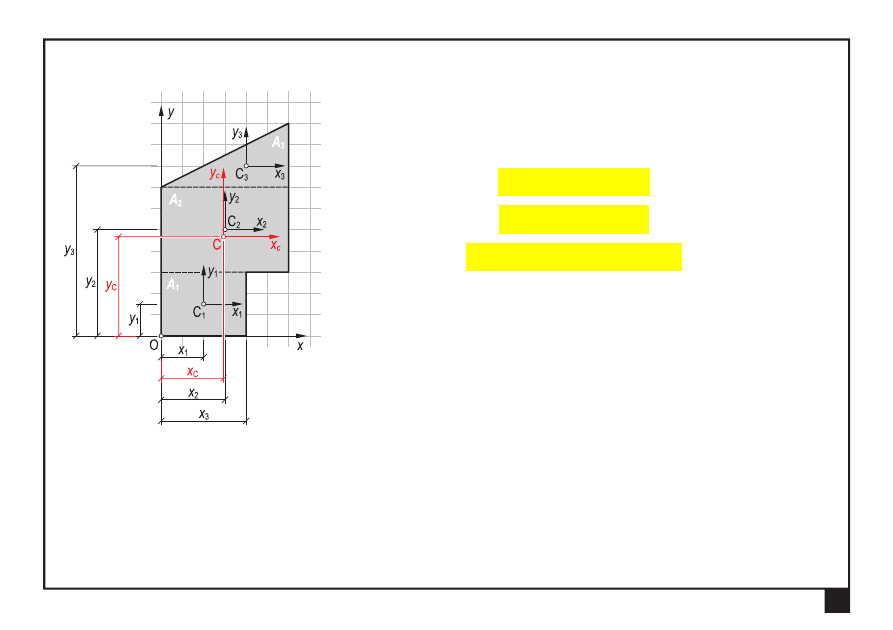
W przypadku figury złożonej z figur regularnych twierdzenie

Steinera dla i-tej figury składowej możemy zapisać w następującej
postaci:

2

C

)

(

)

(

y

y

A

I

I

i

i

x

i

x

i

c

−

+

=

(1.19)

2

C

)

(

)

(

x

x

A

I

I

i

i

y

i

y

i

c

−

+

=

(1.20)

)

)(

(

C

C

)

(

y

y

x

x

A

I

I

i

i

i

y

x

i

y

x

i

i

c

c

−

−

+

=

(1.21)

gdzie:

)

(

)

(

)

(

,

,

i

y

x

i

y

i

x

c

c

c

c

I

I

I

— momenty bezwładności i moment dewiacji

i-tej

figury regularnej względem osi centralnych

c

c

y

x

,

figury złożonej,

i

i

i

i

y

x

y

x

I

I

I

,

,

— centralne momenty bezwładności i moment dewiacji

i-tej figury regularnej względem osi

i

i

y

x

,

,

i

A

—

pole

powierzchni

i-tej figury regularnej,

i

i

y

x

,

—

odległości lokalnych osi centralnych

i

i

x

y

,

od osi dowolnego układu współrzędnych

x

y

,

,

C

C

,

y

x

—

odległości centralnych

c

c

x

y

,

figury złożonej

od osi dowolnego układu współrzędnych

x

y

,

.

Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

11

Obrót osi centralnych

Centralne momenty bezwładności

c

x

I

,

c

y

I

oraz centralny moment dewiacji

c

c

y

x

I

są równe:

∫

=

A

x

A

y

I

c

d

2

,

∫

=

A

y

A

x

I

c

d

2

,

∫

=

A

y

x

A

xy

I

c

c

d

Momenty bezwładności

ξ

I

,

η

I

oraz moment dewiacji

ξη

I

względem osi obróconych o kąt

φ

:

∫

=

A

ξ

A

η

I

d

2

,

∫

=

A

η

A

ξ

I

d

2

,

∫

=

A

ξη

A

η

ξ

I

d

Podstawiamy

φ

y

φ

x

ξ

sin

cos

+

=

oraz

φ

x

φ

y

η

sin

cos

−

=

∫

∫

∫

∫

∫

∫

∫

+

−

=

=

+

−

=

=

−

=

A

A

A

A

A

A

A

ξ

A

x

φ

A

xy

φ

φ

A

y

φ

A

φ

x

A

φ

φ

y

x

A

φ

y

A

φ

x

φ

y

I

d

sin

d

cos

sin

2

d

cos

d

sin

d

cos

sin

2

d

cos

d

)

sin

cos

(

2

2

2

2

2

2

2

2

2

φ

I

φ

φ

I

φ

I

I

c

c

c

c

y

y

x

x

ξ

2

2

sin

cos

sin

2

cos

+

−

=

φ

I

φ

φ

I

φ

I

I

c

c

c

c

y

y

x

x

η

2

2

cos

cos

sin

2

sin

+

+

=

Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

12

Obrót osi centralnych

∫

∫

∫

∫

∫

∫

∫

∫

−

+

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

=

=

−

+

−

=

=

−

+

=

A

A

A

A

A

A

A

A

ξη

A

xy

φ

φ

A

x

A

y

φ

φ

A

φ

xy

A

φ

φ

y

A

φ

φ

x

A

φ

xy

A

φ

x

φ

y

φ

y

φ

x

I

d

)

sin

(cos

d

d

cos

sin

d

sin

d

cos

sin

d

cos

sin

d

cos

d

)

sin

cos

)(

sin

cos

(

2

2

2

2

2

2

2

2

)

sin

(cos

cos

sin

)

(

2

2

φ

φ

I

φ

φ

I

I

I

c

c

c

c

y

x

y

x

ξη

−

+

−

=

Podstawiamy

φ

φ

φ

2

sin

cos

sin

2

=

,

2

2

cos

1

sin

2

φ

φ

−

=

,

2

2

cos

1

cos

2

φ

φ

+

=

φ

I

φ

I

I

I

I

I

c

c

c

c

c

c

y

x

y

x

y

x

ξ

2

sin

2

cos

)

(

2

1

)

(

2

1

−

−

+

+

=

(1.22)

φ

I

φ

I

I

I

I

I

c

c

c

c

c

c

y

x

y

x

y

x

η

2

sin

2

cos

)

(

2

1

)

(

2

1

+

−

−

+

=

(1.23)

φ

I

φ

I

I

I

c

c

c

c

y

x

y

x

ξη

2

cos

2

sin

)

(

2

1

+

−

=

(1.24)

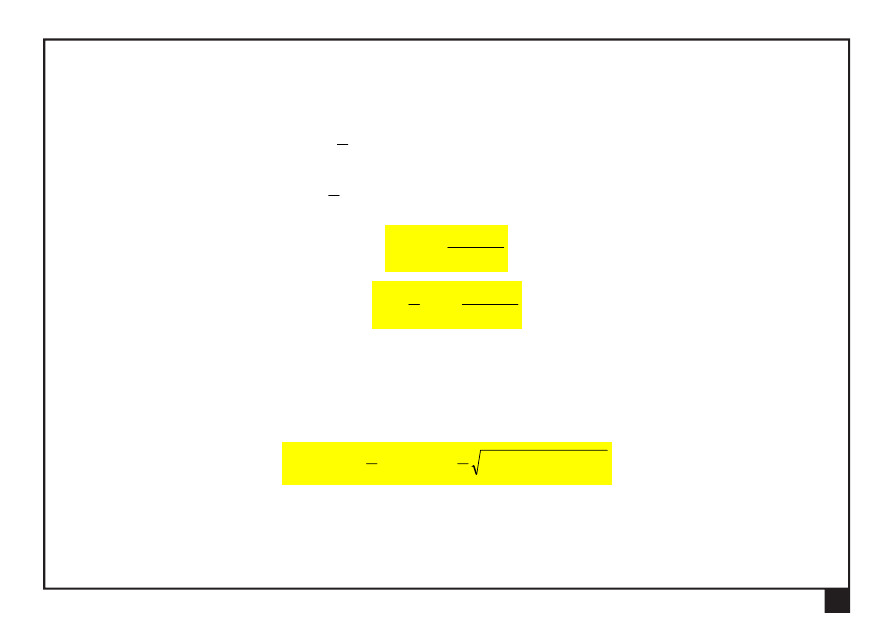
Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

13

Obrót osi centralnych — główne centralne osie i momenty bezwładności

Wyznaczmy takie położenie układu osi ξη

O

(taki kąt

0

φ

), dla którego moment dewiacji

ξη

I

jest równy zeru:

0

2

cos

2

sin

)

(

2

1

0

0

=

+

−

=

φ

I

φ

I

I

I

c

c

c

c

y

x

y

x

ξη

0

0

2

cos

2

sin

)

(

2

1

φ

I

φ

I

I

c

c

c

c

y

x

y

x

−

=

−

c

c

c

c

x

y

y

x

I

I

I

φ

−

=

2

2

tg

0

(1.25)

c

c

c

c

x

y

y

x

I

I

I

φ

−

=

2

arctg

2

1

0

(1.26)

Osie (

η

ξ ,

) układu obróconego o kąt

0

φ

nazywamy

głównymi centralnymi osiami bezwładności i ozna-

czamy cyframi 1 i 2. Momenty bezwładności względem tych osi osiągają wartości ekstremalne —
maksymalną

1

I

oraz minimalną

2

I

:

2

2

min

max

2

,

1

4

)

(

2

1

)

(

2

1

c

c

c

c

c

c

y

x

y

x

y

x

I

I

I

I

I

I

I

+

−

±

+

=

=

(1.27)

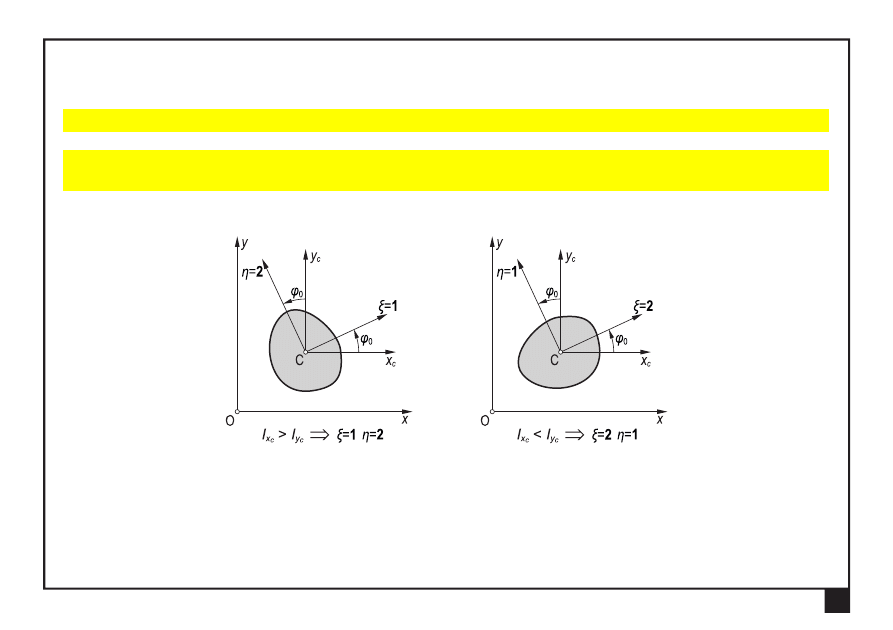
Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

14

Główne centralne osie i momenty bezwładności

Każda oś symetrii figury płaskiej jest jej główną centralną osią bezwładności.

Drugą główną centralną osią bezwładności jest oś prostopadła do osi symetrii

i przechodząca przez środek masy figury płaskiej.

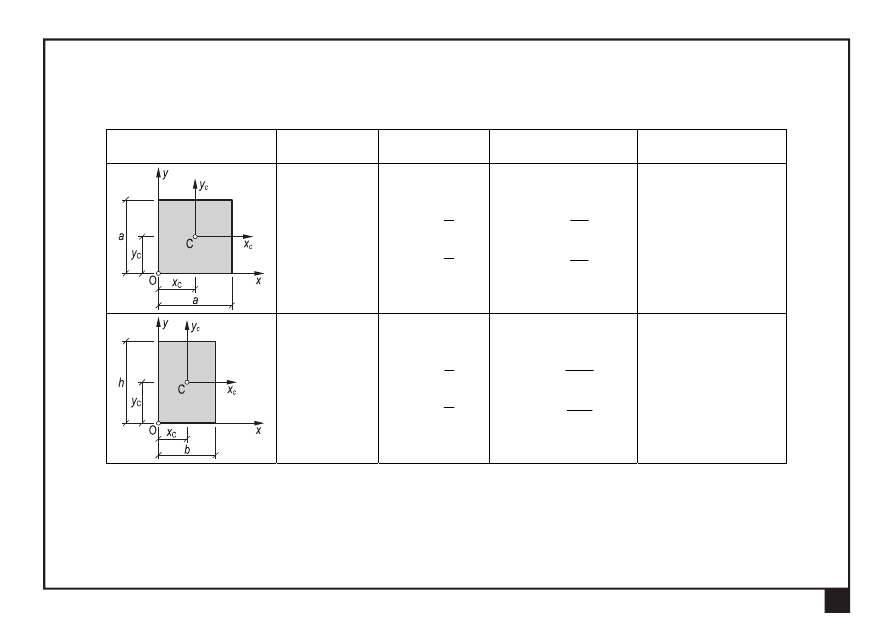
Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

15

Centralne momenty bezwładności wybranych figur regularnych

Tabela 1.1. Charakterystyki geometryczne wybranych figur regularnych

Figura

Pole

powierzchni

Współrzędne
środka masy

Centralne momenty

bezwładności

Centralny moment

dewiacji

2

a

A =

2

C

a

x =

2

C

a

y =

12

4

a

I

c

x

=

12

4

a

I

c

y

=

0

=

c

c

y

x

I

h

b

A =

2

C

b

x =

2

C

h

y =

12

3

h

b

I

c

x

=

12

3

h

b

I

c

y

=

0

=

c

c

y

x

I

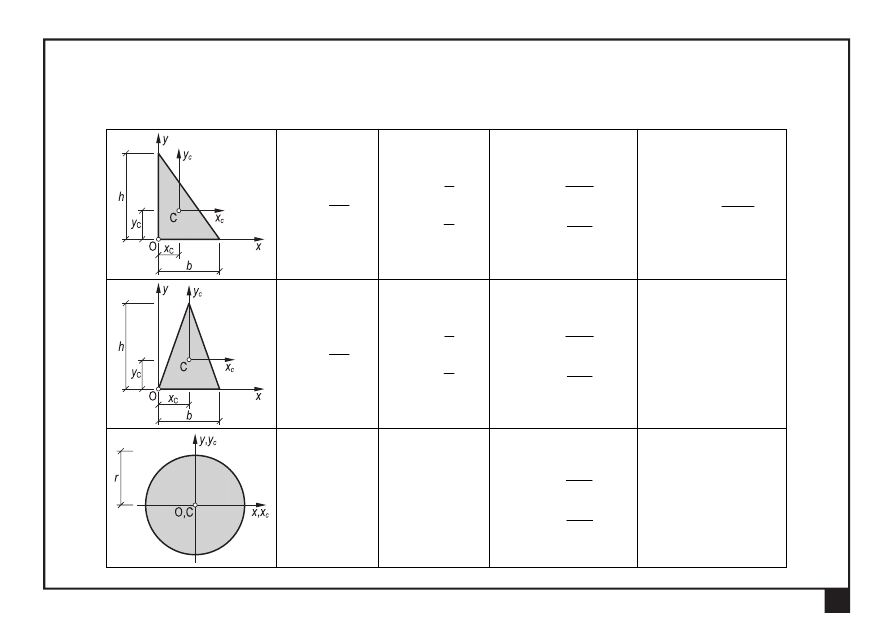
Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

16

Centralne momenty bezwładności wybranych figur regularnych

Tabela 1.1. Charakterystyki geometryczne wybranych figur regularnych

2

h

b

A =

3

C

b

x =

3

C

h

y =

36

3

h

b

I

c

x

=

36

3

h

b

I

c

y

=

72

2

2

h

b

I

c

c

y

x

−

=

2

h

b

A =

2

C

b

x =

3

C

h

y =

36

3

h

b

I

c

x

=

36

3

h

b

I

c

y

=

0

=

c

c

y

x

I

2

r

π

A =

0

C

=

x

0

C

=

y

4

4

r

π

I

c

x

=

4

4

r

π

I

c

y

=

0

=

c

c

y

x

I

Środek masy i geometryczne momenty bezwładności figur płaskich. Główne centralne osie i momenty bezwładności

BIBLIOGRAFIA
Dyląg Z., Jakubowicz A., Orłoś Z.,

Wytrzymałość materiałów, tom I, WNT, Warszawa 1999.

Klasztorny M.,

Skrypt do wytrzymałości materiałów [w przygotowaniu].