KATEDRA MECHANIKI STOSOWANEJ

Zakład Mechaniki Ogólnej i Biomechaniki

Wydział Mechaniczny Technologiczny

POLITECHNIKA ŚLĄSKA

INSTRUKCJA DO ĆWICZEŃ TABLICOWYCH

Przedmiot:
MECHANIKA

Kod przedmiotu: A0PT11P00D11

Kod ćwiczenia:
Nr ćwiczenia: 7

Temat:
Płaskie układy sił z tarciem

Kierunek:

AiR

Specjalizacja:

-

1.

Ćwiczenie

Celem ćwiczenia jest zapoznanie studentów z płaskimi układami sił z tarciem oraz przedstawienie sposobu
rozwiązywania układów płaskich w których występuje tarcie.

2.

Wyposażenie stanowiska

•

Tablica

•

Rzutnik

•

Folie i kserokopie schematów zadań

3.

Przebieg ćwiczenia

•

Omówienie tarcia ślizgowego – podstawowe pojęcia i równania

•

Omówienie tarcia cięgna o krążek – równanie Eulera

•

Omówienie tarcia tocznego – podstawowe pojęcia i równania

•

Rozwijanie i ćwiczenie umiejętności rozwiązywania zadań z omówionych zagadnień.

LITERATURA:

[1] Leyko J, Szmeltera J.: Zbiór zadań z mechaniki, PWN, Warszawa 1980
[2] Mieszczerski I. W.: Zbiór zadań z mechaniki, Państwowe Wydawnictwa Naukowe, Warszawa 1971
[3] Misiak J.: Zadania z mechaniki ogólnej, część I - statyka, Wydawnictwa Naukowo - Techniczne, Warszawa

1994.

[4] Niezgodziński M., Niezgodziński T., Walczak W.: Mechanika ogólna w zadaniach, Wydawnictwo Politechniki

Łódzkiej, Łódź 1994

[5] Nizioł J.: Metodyka rozwiązywania zadań z mechaniki, Wydawnictwa Naukowo - Techniczne, Warszawa 2002

Opracował:
mgr inż. Paweł Potkowa

Sprawdził:
Prof. dr hab. inż. Dagmara Tejszerska

Zatwierdził:
Prof. dr hab. inż. Dagmara Tejszerska

Uwagi:
Załącznikiem są tematy zadań

ZAŁĄCZNIK DO ĆWICZEŃ TABLICOWYCH Nr 9

Równowaga przestrzennego zbieżnego układu sił – cz.1

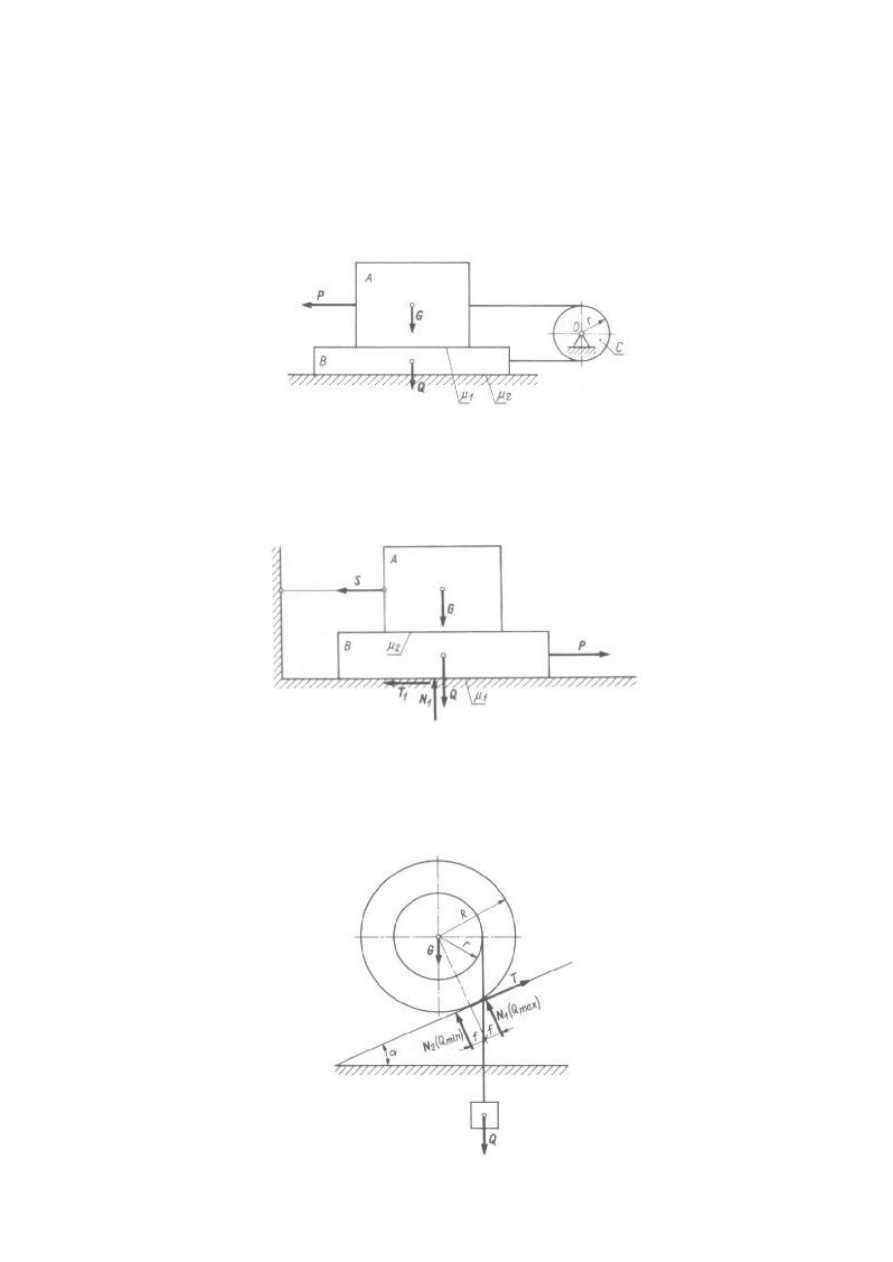
Zadanie 1

Ciało A o ciężarze G położono na płycie B o ciężarze Q i połączono je nieważkim cięgnem wiotkim przerzuconym przez krążek
C. Obliczyć maksymalną wartość poziomej siły P przyłożonej do ciała A, przy której ciało A będzie pozostawać w spoczynku,
jeżeli współczynnik tarcia ślizgowego (statycznego) ciała A o płytę B wynosi

µ

1

, a płyty B o podłoże

µ

2

. Tarcie cięgna o krążek C

należy pominąć. Ponadto wyznaczyć napięcie cięgna S

1

i S

2

, reakcje normalne N

1

i N

2

oraz siły tarcia T

1

i T

2

.

Zadanie 2

Ciało A o ciężarze G=3 kN położono na płycie B o ciężarze Q=5 kN i umocowano je nieważkim cięgnem do pionowej ściany.
Obliczyć maksymalną wartość poziomej siły P w położeniu równowagi, przyłożonej do płyty B, jeżeli współczynnik tarcia
ślizgowego (statycznego) płyty B o podłoże wynosi

µ

1

=0,35, a ciała A o płytę B

µ

2

=0,15. Ponadto obliczyć napięcie cięgna S.

Zadanie 3

Dwie współśrodkowo zamocowane tarcze kołowe o łącznym ciężarze G ustawiono na równi nachylonej do poziomu pod kątem

α

.

Na tarczę o promieniu r nawinięto nić, na końcu której zawieszono ciało o ciężarze Q. Podać, w jakich granicach może zmieniać
się wartość ciężaru Q, aby istniała równowaga, jeżeli współczynnik tarcia tocznego przy toczeniu się tarczy po równi wynosi f, a
współczynnik tarcia ślizgowego (statycznego) wynosi

µ

.

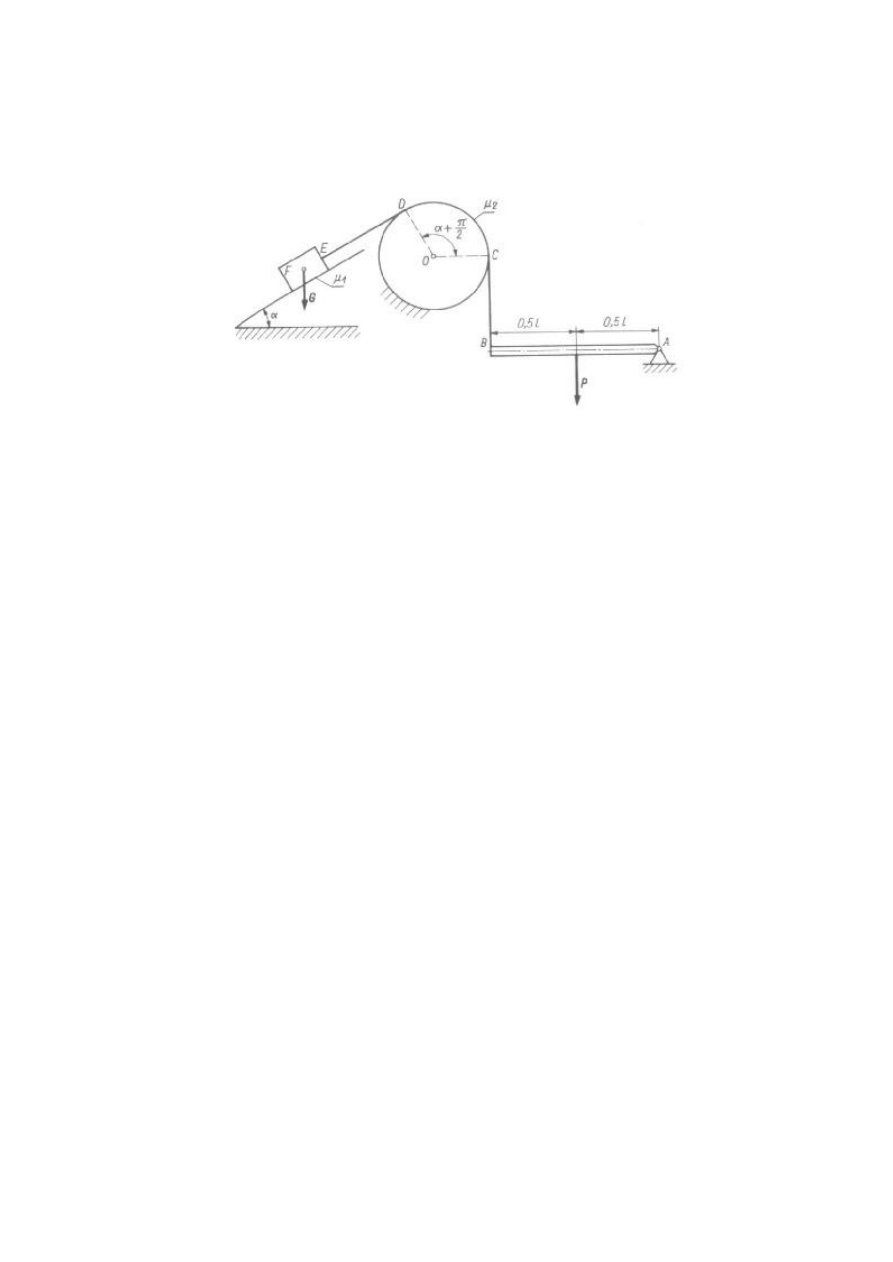
Zadanie 4

Nieważki pręt AB o długości l opiera się w punkcie A na stałej podporze przegubowej. Na końcu pręta w punkcie B
przymocowano cięgno, które przerzucono przez chropowaty krążek i na jego końcu E przywiązano ciało F o ciężarze G, leżące
na równi pochyłej tworzącej z poziomem kąt

α

=30

°

. Współczynnik tarcia ślizgowego ciała F o równię wynosi

µ

1

, a cięgna o

powierzchnię krążka

µ

2

. Wyznaczyć, w jakich granicach musi się mieścić wartość pionowej siły P, przyłożonej w środku pręta

AB, aby zachodziła równowaga.