Mechanika ogólna
Mechanika ogólna
1
1
Wykład nr 4
Wykład nr 4
Reakcje w układach z przegubami.
Reakcje w układach z przegubami.
Reakcje
Reakcje –
– belki
belki
przegubowe
przegubowe
(1)
(1)
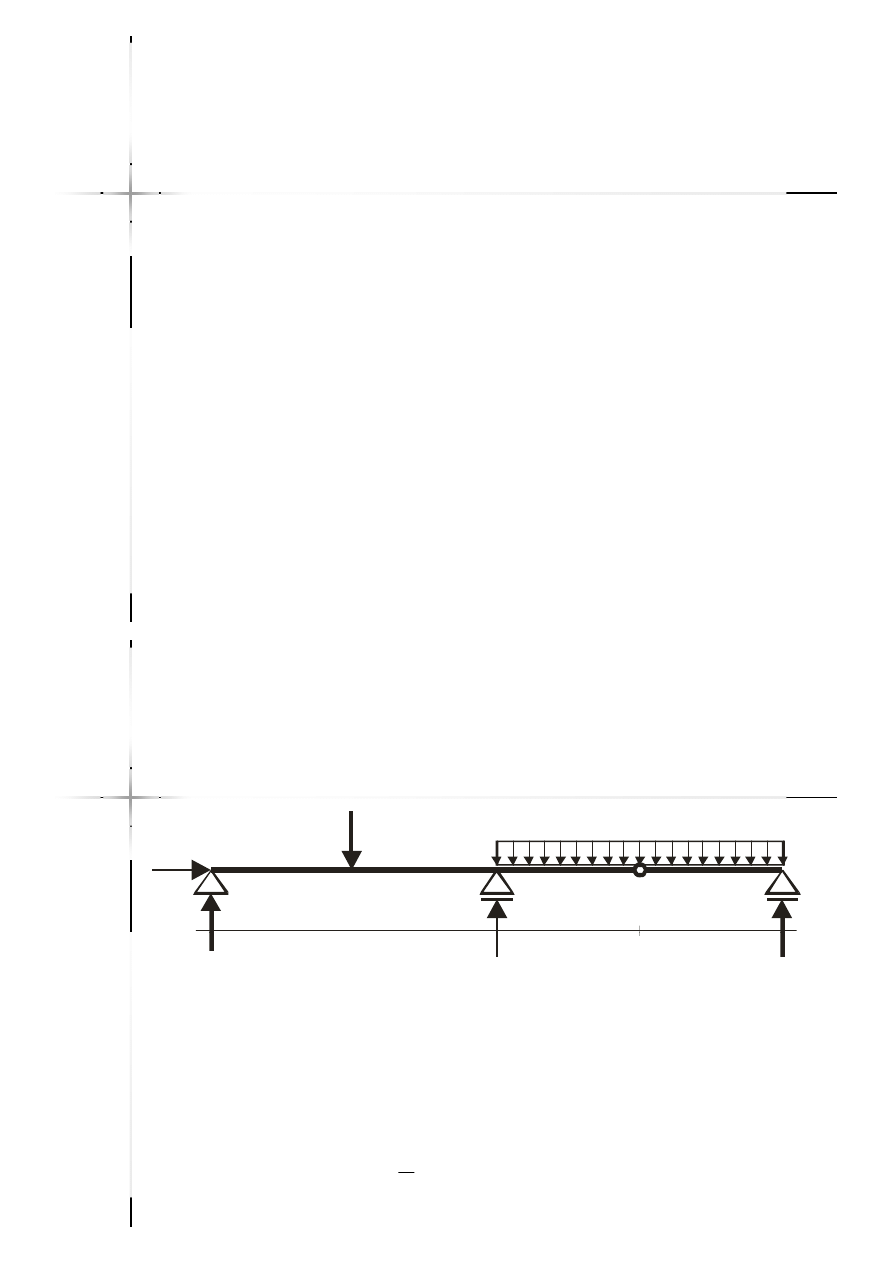
l
P
l
l
l
q
A
B
C
D
V
H
A
2
2
0
:
A
H
X
0
2
:
l
q
P
R
R
V
Y
D
B
A
0
2
:
l
l
q
l
R
M
D
p
C
0
3
2
4
2
:
l
l
q
l
P
l
R
l
R
M
D
B
A
V
A
R
B
R
D

Rozwiązanie
Rozwiązanie
0
:
A
H
X
2
0
2
:
l
q
R
l
l
q
l
R
M
D
D
p
C
3
3
2
2
2
2
2
2
2
0
2
:
l
q
P
l
q
l
q
P
l
q
P
R
R
l
q
P
V
l
q
P
R
R
V
Y
D
B
A
D
B
A
l
q
P
l
q
P
R
l
l
l
q
l
P
l
R
R
l
l
q
l
P
l
R
l
R
M
D
D
B
D
B
A
2
2
3
2
2
2
3
2
4
0
3
2
4
2
:
Podstawienie danych
Podstawienie danych
m
l
kN
P
m
kN
q
2
10
/
5
0
A
H
4
4
0
A
H
0
2
2
/
5
2
10
m
m
kN
kN
V
A
kN
m
m
kN
l
q
R
D
5
2
2
/
5
2
kN
m
m
kN
kN
l
q
P
R
B
25
2
2
/
5
2
10
2
2
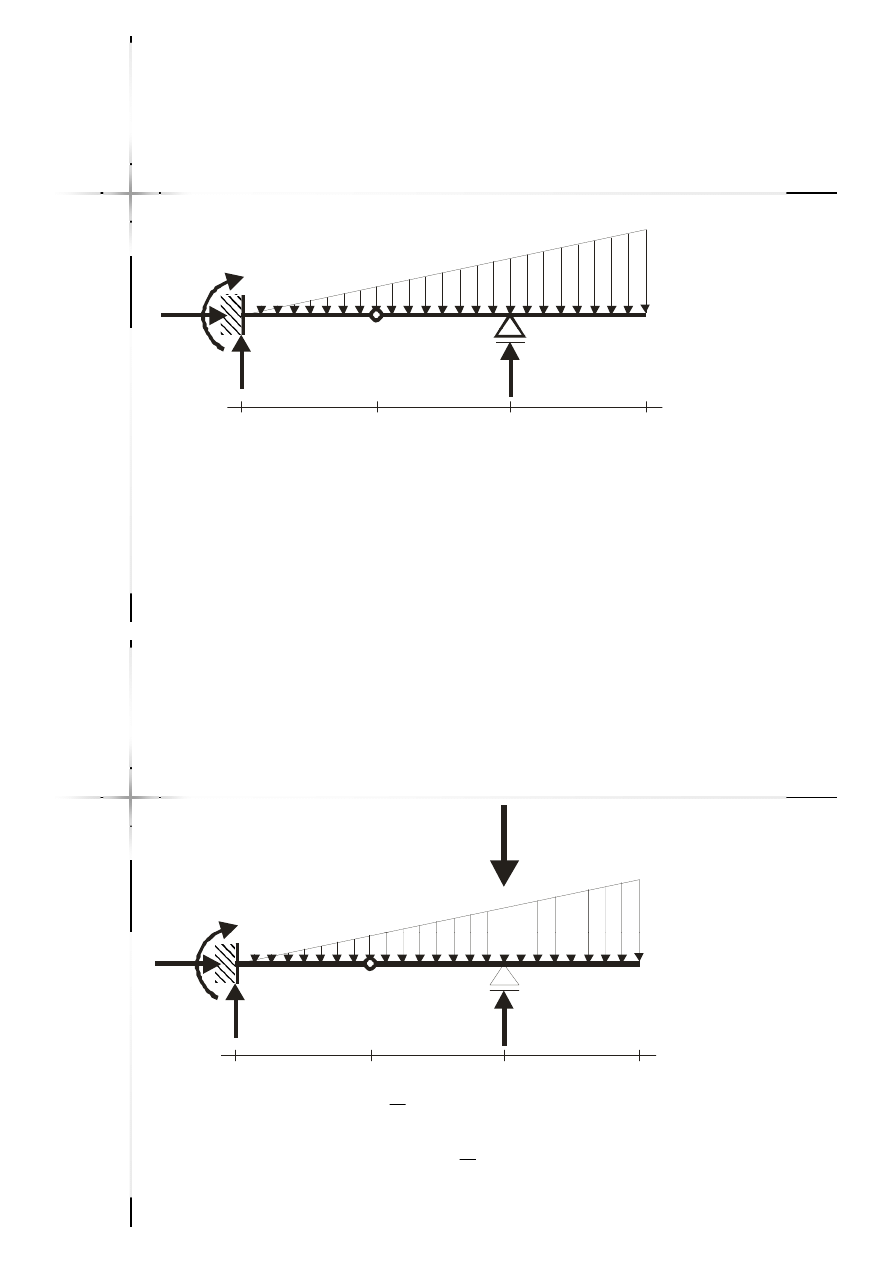
Reakcje
Reakcje –
– belki
belki
przegubowe
przegubowe
(2)
(2)
q
H
A
M
A
5
5
V
A
R
B
l
l
l
0
:
A
H
X
Wypadkowa obciążenia
Wypadkowa obciążenia
trójkątnego
trójkątnego
q
M
A
½
q 3l
·
6
6
0
3
2
1
:
l
q
R
V
Y
B
A
0
2
3
2
1
2
:
l
l
q
M
l
R
M
A
B
A
V
A
H
A
A
R
B
l
l
l
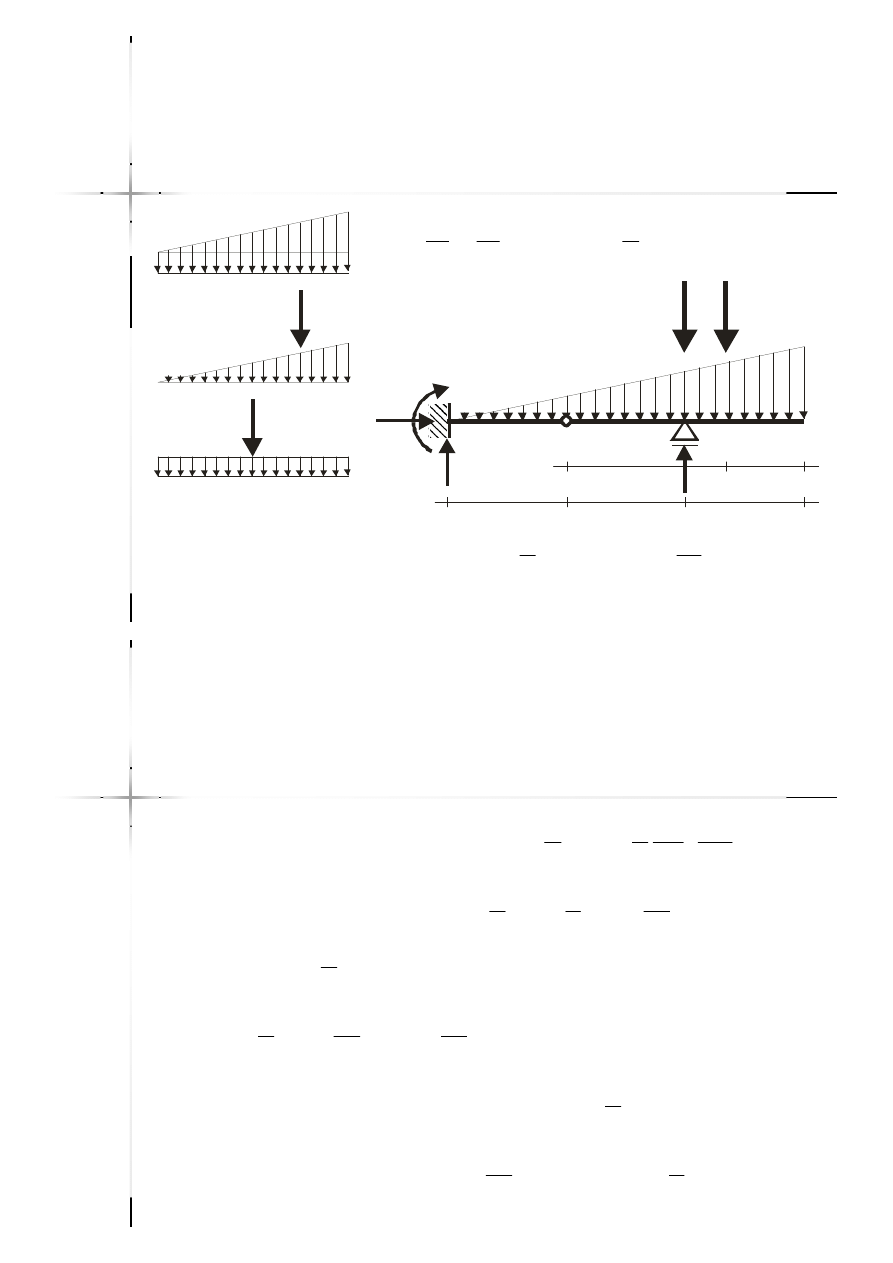
Suma momentów
Suma momentów
względem przegubu
względem przegubu
q
q
’
=
q
- ’
q
½( - ’)
q q
l
·2
q
q
l
’·2
½( - ’)
q q
l
·2
3
3
q
q
l
q
l
q
7
7
0
3
2
2
2
2
1
2
:
l
l
q
q
l
l
q
l
R
M
B
p
C
q
- ’
q
+
q
’
q
’
q
l
’·2
q
V
A
H
A
M
A
R
B
l
2l 3
/
C
l
l
2
·
2l 3
/
q
’
Rozwiązanie
Rozwiązanie
0
:
A
H
X
ql
ql
ql
R
l
q
l
q
l
R
M
B
B
p
C
9
14
9
8
3
2
0
3
8
3
2
2
1
2
3
:
2
2
8
8
ql
ql
ql
V
l
q
R
V
Y
A
B
A
18
1
9
14
2
3
0
3
2
1
:
2
2
2
9
1
3
2
9
14
0
2
3
2
1
2
:
ql
ql
ql
M
l
l
q
M
l
R
M
A
A
B
A
9
9
3
Podstawienie danych
Podstawienie danych
m
l
m
kN
q
5
,
1
/
10
0
A
H
9
9
0
A
H
kN
m
m
kN
ql
V
A
833
,
0
5
,
1
/
10
18
1
18
1
kNm
m
m
kN
ql
M
A
5
,
2
5
,
1
/
10
9
1
9
1
2
2
kN
m
m
kN
ql
R
B
333
,
23
5
,
1
/
10
9
14
9
14
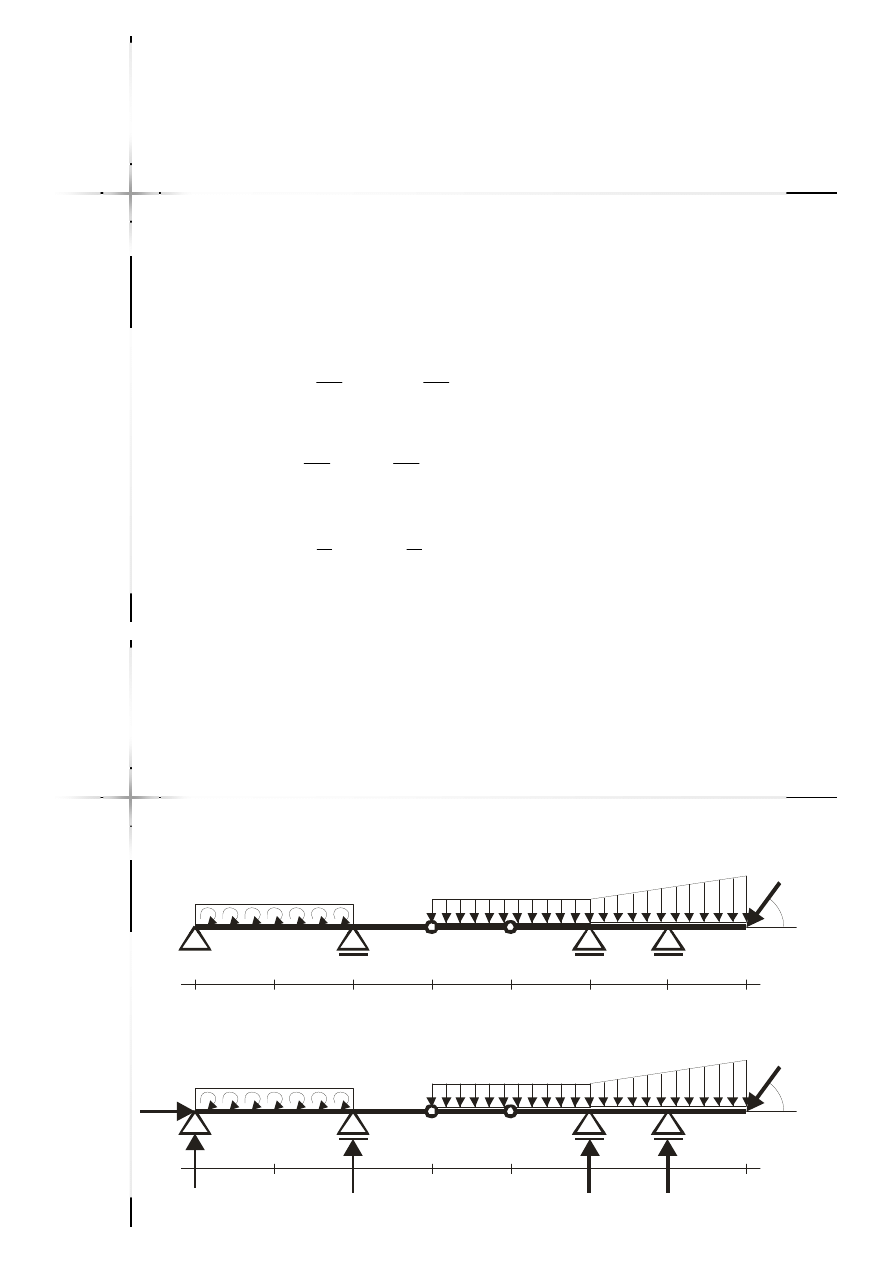
Belki przegubowe
Belki przegubowe
(3)
(3)
Sąsiadujące przeguby
Sąsiadujące przeguby
P
q
A
B
E
m
2q
F
q
10
10
l
P
l
l
l
l
l
l
q
A
B
C
E
V
A
H
A
R
B
R
E
m
D
2q
F
R
F
q
l
l
l
l
l
l
l
A
B
C
E
D
F
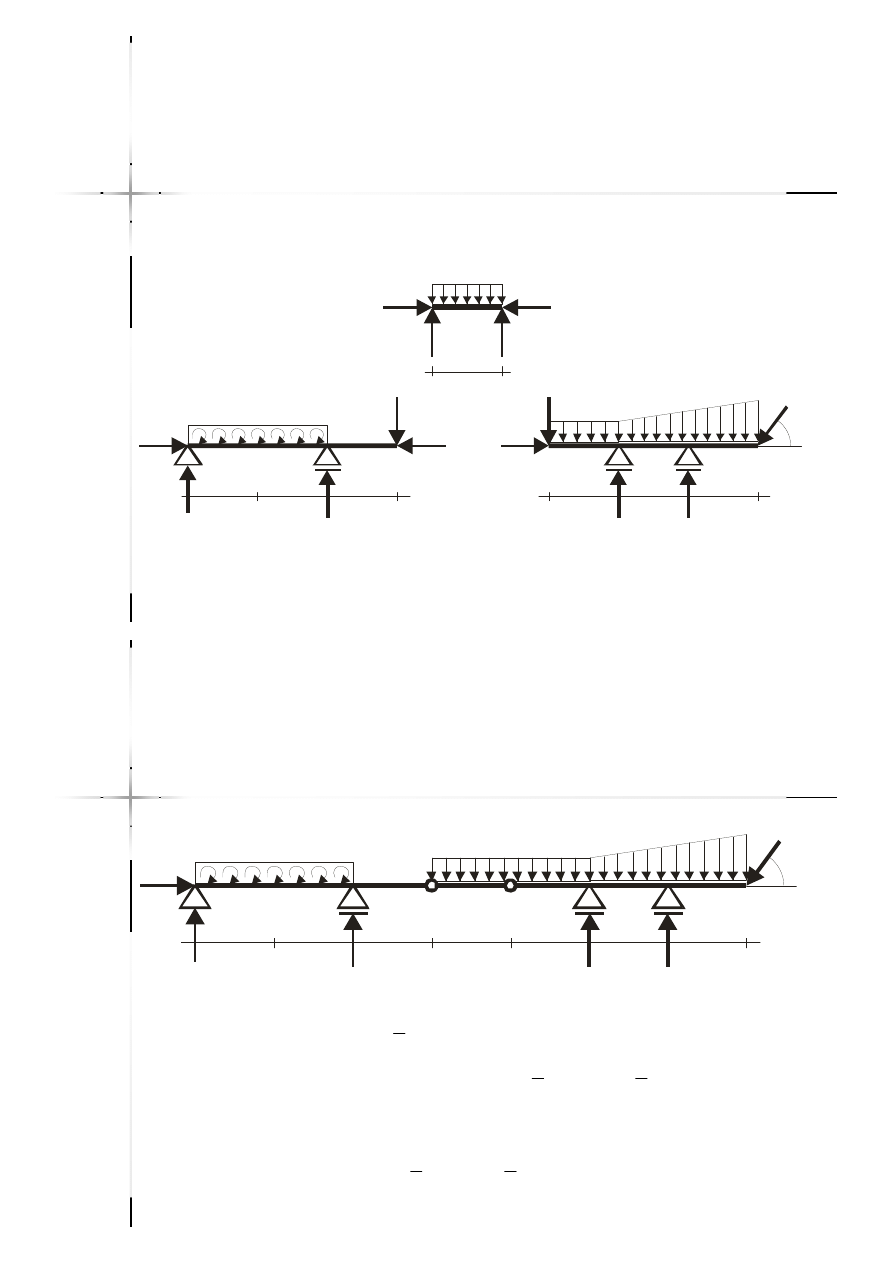
Belki proste
Belki proste –
– równania
równania
równowagi
równowagi
C
H
C
V
q
D
H
D
V
0
X
0
Y
9 niewiadomych
9 niewiadomych –– 9 równań
9 równań
11
11
H
C
V
C
V
C
l
P
l
l
l
l
l
l
q
A
B
C
E
V
A
H
A
R
B
R
E
m
D
2q
F
R
F
q
V
D
H
D
V
D
0
Y
0
C
M
0
X
0
Y
0
A
M
0
X
0
Y
0
D
M
Reakcje
Reakcje –
– belki
belki
przegubowe
przegubowe
(3)
(3)
l
P
l
l
l
l
l
l
q
A
B
C
E
V
H
A
m
D
2q
F
q
12
12
l
l
l
l
l
l
l
V
A
R
B
R
E
R
F
0
cos
:
P
H
X
A
0
sin
2
2
1
4
:
P
l
q
l
q
R
R
R
V
Y
F
E
B
A
0
2
3
:
l
m
l
R
l
V
M
B
A
l
C
0
7
sin
2
3
2
5
2
2
1
5
4
2
6
5
2
:
l
P
l
l
l
q
l
l
q
l
m
l
R
l
R
l
R
M
F
E
B
A
0
3
sin
2
3
2
2
2
1
5
,
1
3
2
:
l
P
l
l
l
q
l
l
q
l
R
l
R
M
F
E
p
D
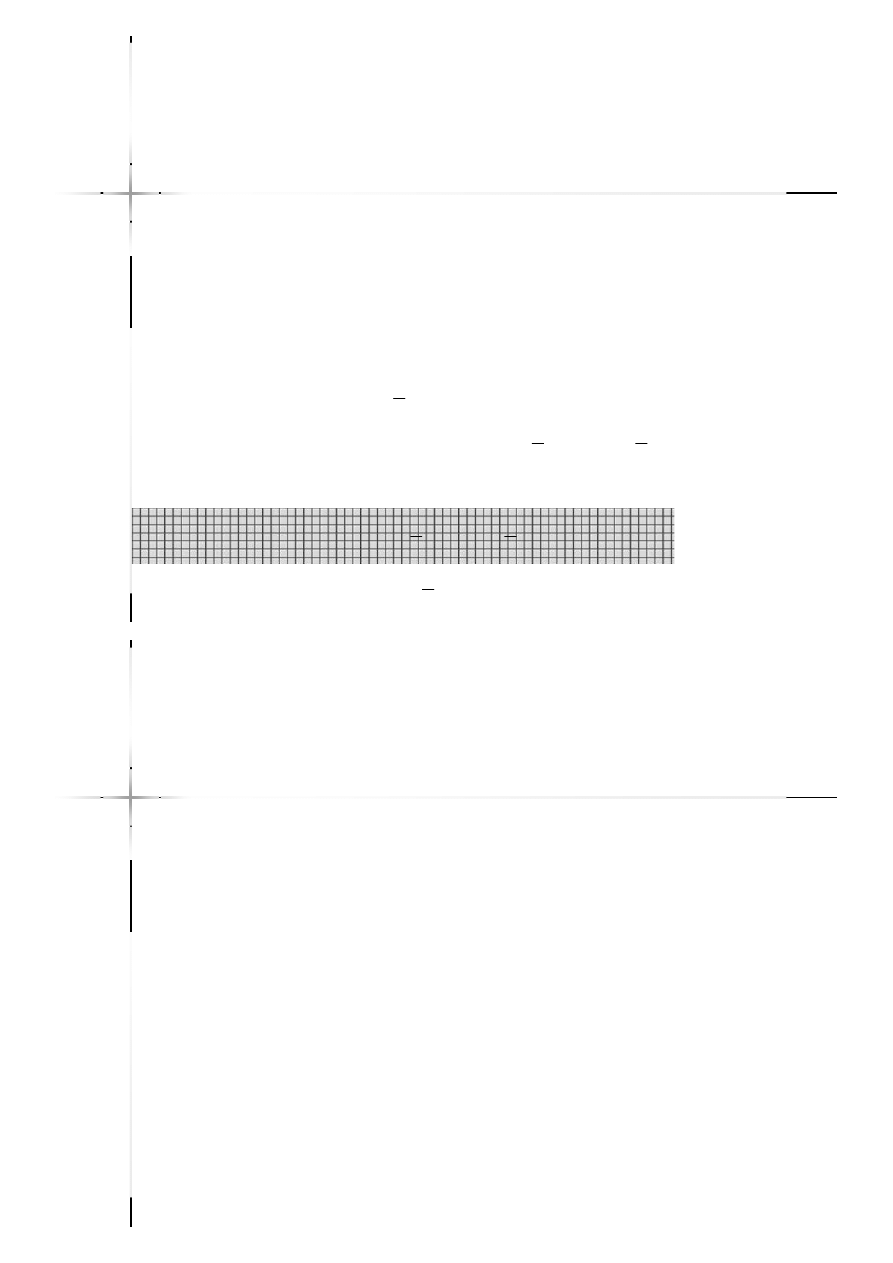
Równania względem sąsiadujących
Równania względem sąsiadujących
przegubów lepiej zapisać z tej samej
przegubów lepiej zapisać z tej samej
strony.
strony.
Sąsiadujące przeguby
Sąsiadujące przeguby –
–
łatwość rozwiązania
łatwość rozwiązania
13
13
strony.
strony.
0
cos
:
P
H
X
A
0
sin
2
2
1
4
:
P
l
q
l
q
R
R
R
V
Y
F
E
B
A
0
2
3
:
l
m
l
R
l
V
M
B
A
l
C
0
7
sin
2
3
2
5
2
2
1
5
4
2
6
5
2
:
l
P
l
l
l
q
l
l
q
l
m
l
R
l
R
l
R
M
F
E
B
A
0
3
sin
2
3
2
2
2
1
5
,
1
3
2
:
l
P
l
l
l
q
l
l
q
l
R
l
R
M
F
E
p
D
0
2
1
2
2
4
:
l
l
q
l
m
l
R
l
V
M
B
A
l
D
Rozwiązanie
Rozwiązanie
kN
H
A
5
m
kNm
m
m
kN
q
kN
P
/
5
/
5
10
14
14
kN
V
A
25
,
6
kN
R
B
75
,
8
kN
R
F
987
,
28
m
l
m
kNm
m
1
/
5
kN
R
E
173
,
2

Zasady pisania dodatkowych
Zasady pisania dodatkowych
równań dla przegubów
równań dla przegubów
(1)
(1)
Dodatkowe równanie względem
Dodatkowe równanie względem
przegubu musi wykorzystywać
przegubu musi wykorzystywać
własność przegubu, tj. że moment w
własność przegubu, tj. że moment w
15
15
własność przegubu, tj. że moment w
własność przegubu, tj. że moment w
przegubie równy jest 0, a więc
przegubie równy jest 0, a więc
dodatkowe równanie nie może być
dodatkowe równanie nie może być
zwykłą sumą momentów względem
zwykłą sumą momentów względem
przegubu, a musi być sumą
przegubu, a musi być sumą
momentów od sił z jednej strony
momentów od sił z jednej strony
przegubu.
przegubu.
Zasady pisania dodatkowych
Zasady pisania dodatkowych
równań dla przegubów
równań dla przegubów
(2)
(2)
Każdy przegub musi zostać
Każdy przegub musi zostać
wykorzystany co najmniej jeden raz.
wykorzystany co najmniej jeden raz.
Jeżeli chcemy zapisać równanie dla
Jeżeli chcemy zapisać równanie dla
16
16
Jeżeli chcemy zapisać równanie dla
Jeżeli chcemy zapisać równanie dla
przegubu z drugiej strony, to
przegubu z drugiej strony, to
zastępuje ono jedno z równań
zastępuje ono jedno z równań
podstawowych (sumę momentów
podstawowych (sumę momentów
względem dowolnego punktu).
względem dowolnego punktu).
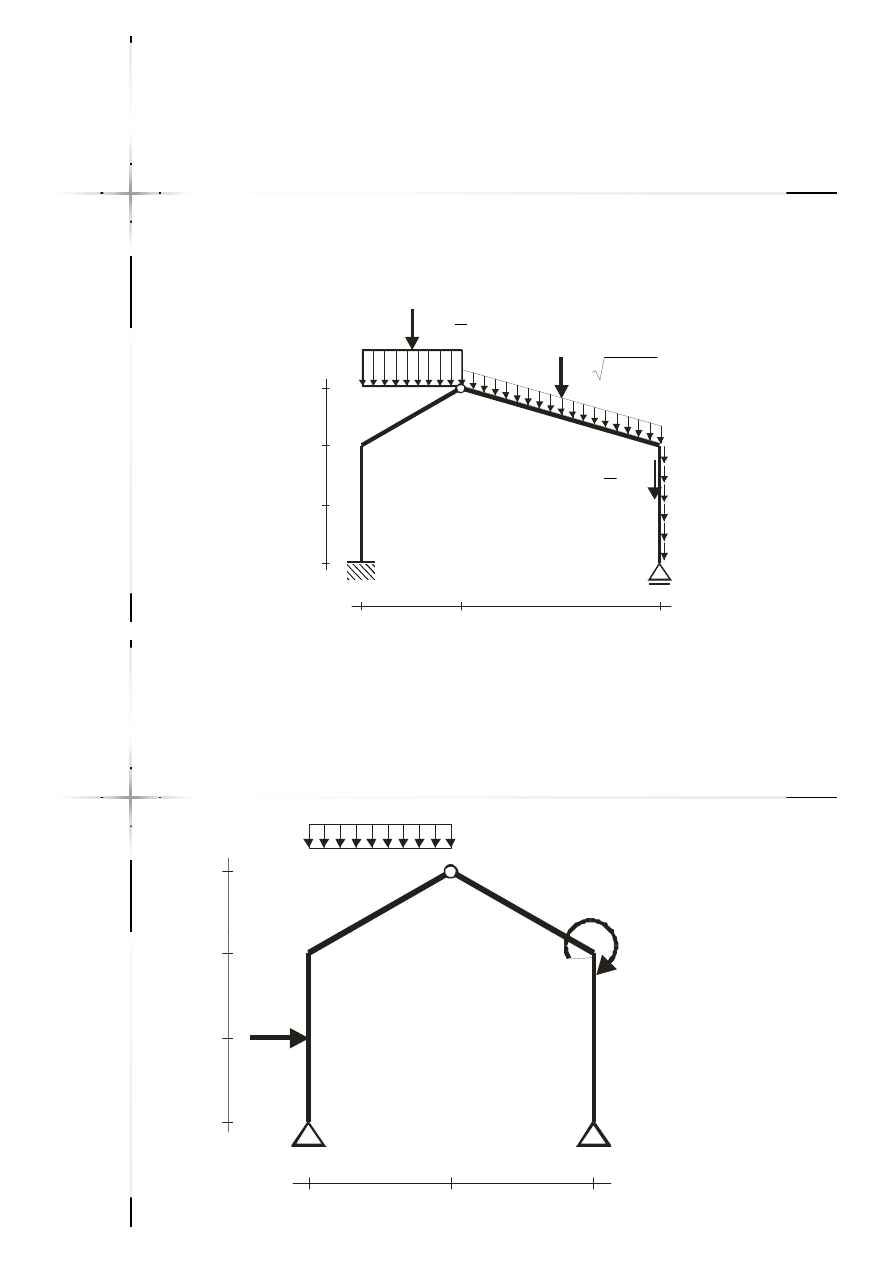
Inne rodzaje obciążeń
Inne rodzaje obciążeń
Obciążenie osiowe rozłożone wzdłuż pręta.
Obciążenie osiowe rozłożone wzdłuż pręta.
Obciążenie pionowe na pręcie ukośnym:
Obciążenie pionowe na pręcie ukośnym:
–– intensywność na jednostkę rzutu;
intensywność na jednostkę rzutu;
–– intensywność na jednostkę długości pręta.
intensywność na jednostkę długości pręta.
2q
2
2
l
q
17
17
l
h
h
h
q
q
/2
l
/2
2q
2
2
h
l
q
2
2q
h
q
2
2
Reakcje
Reakcje –
– rama
rama
trójprzegubowa
trójprzegubowa
(1)
(1)
h
q
M
18
18
l
l
P
h
h
M
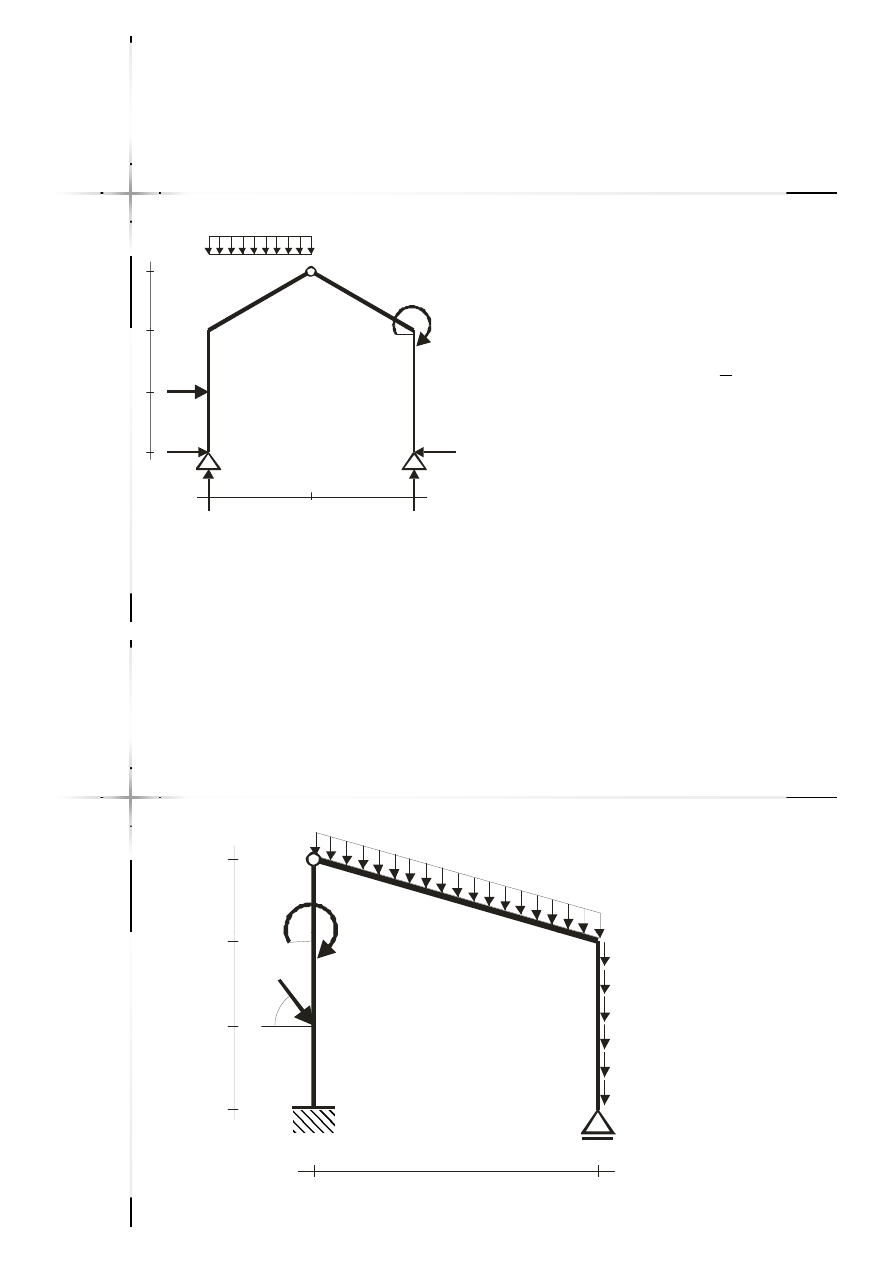
Reakcje
Reakcje –
– rama
rama
trójprzegubowa
trójprzegubowa
(2)
(2)
C
h
q
M
0
:
P
H
H
X
B
A
0
:
l
q
V
V
Y
B
A
19
19
l
l
P
A
B
V
A
H
A
V
B
H
B
h
h
M
0
:
l
q
V
V
Y
B
A
0
3
:
M
h
H
l
V
M
B
B
p
C
0
2
1
2
:
M
l
l
l
q
h
P
l
V
M
A
B
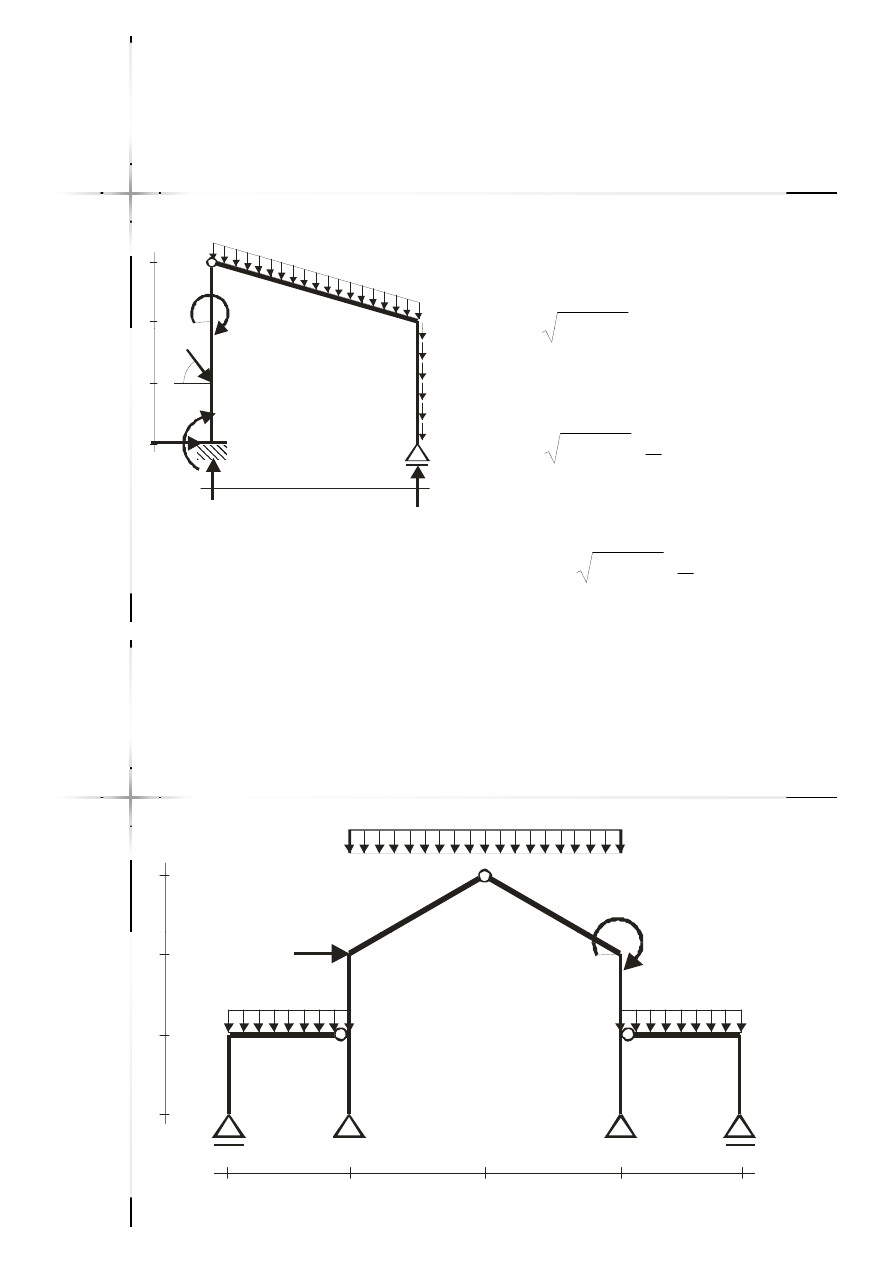
Reakcje
Reakcje –
– rama
rama
przegubowa
przegubowa
(1)
(1)
h
2q
M
20
20
l
h
h
q
M
P
Reakcje
Reakcje –
– rama
rama
przegubowa
przegubowa
(2)
(2)
0
cos
:
P
H
X
A
0
2
2
sin
:
2
2
h
q
h
l
q
P
R
V
Y
B
A
h
2q
M
C
21
21
0
2
2
2
2
h
q
h
l
q
0
2
2
2
:
2
2
l
h
l
q
l
h
q
l
R
M
B
p
C
0
2
2
2
cos
:
2
2
l
R
l
h
q
l
h
l
q
M
h
P
M
M
B
A
A
V
A
H
A
M
A
l
h
h
q
P
R
B
A
B
Rama nawowa
Rama nawowa
h
q
P
M
22
22
l
l
h
h
l
l
q
q
P
M
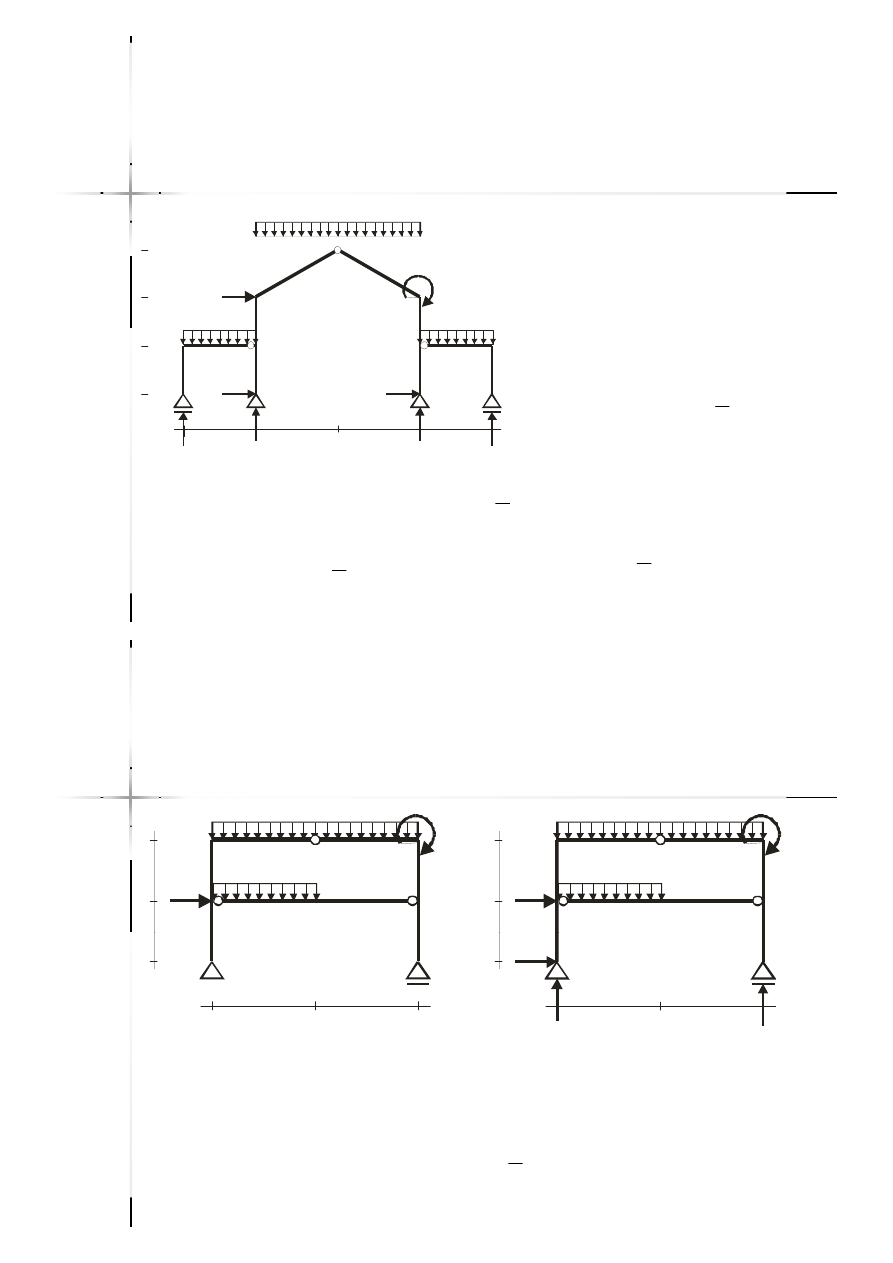
Rama nawowa
Rama nawowa –
–
równania równowagi
równania równowagi
0
:
P
H
H
X
C
B
0
2
:
l
q
l
q
l
q
R
V
V
R
Y
D
C
B
A
h
h
q
q
q
P
M
G
23
23
0
5
,
1
2
2
3
:
l
l
q
M
l
l
q
l
R
h
H
l
V
M
D
C
C
p
G
0
5
,
3
2
2
2
2
4
3
:
l
l
q
l
l
q
l
l
q
M
h
P
l
R
l
V
l
V
M
D
C
B
A
0
2
:
l
l
q
l
R
M
A
l
E
0
2
:
l
l
q
l
R
M
D
p
F
A
l
l
h
h
l
l
V
B
H
B
V
C
H
C
R
A
R
D
C
B
D
E
F
Rama ze ściągiem
Rama ze ściągiem –
– reakcje
reakcje
podporowe (3 niewiadome)
podporowe (3 niewiadome)
P
h
h
2q
M
q
P
h
h
2q
M
q
C
D
E
24
24
l
l
h
0
:
P
H
X
A
0
2
2
:
l
q
l
q
R
V
Y
B
A
0
2
2
2
2
:
l
l
q
l
l
q
M
h
P
l
R
M
B
A
l
l
A
B
V
A
H
A
R
B
h
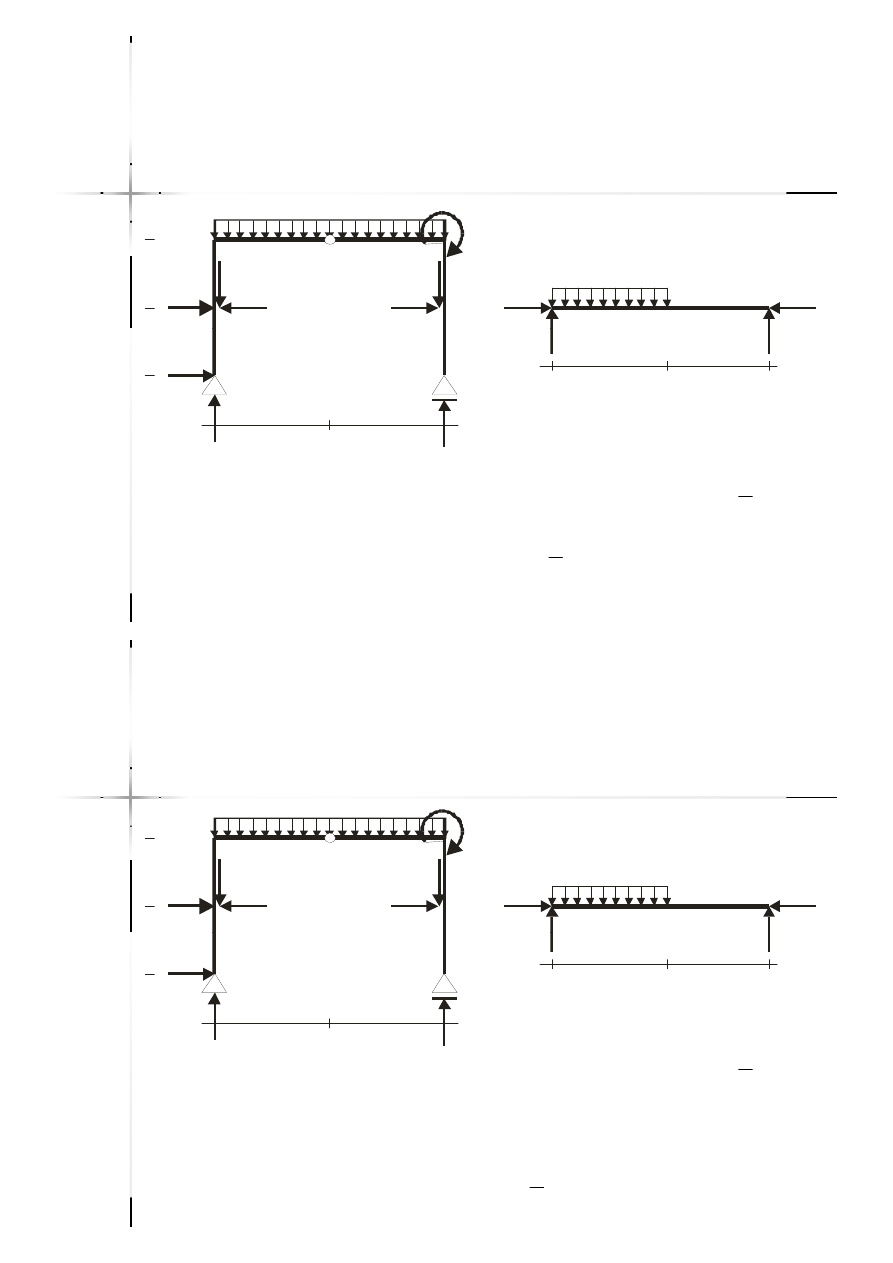
Siły w ściągu
Siły w ściągu –
– cztery
cztery
dodatkowe równania
dodatkowe równania
P
h
2q
M
C
D
E
D
E
q
V
H
D
H
E
V
V
D
H
D
V
E
H
E
25
25
0
:
E
D
H
H
X
0
:
l
q
V
V
Y
E
D
0
2
2
:
l
l
q
l
V
M
E
D
0
2
2
:
l
l
q
M
l
R
h
H
l
V
M
B
E
E
p
C
l
l
A
B
V
A
H
A
R
B
h
V
D
V
E
l
l
Rama ze ściągiem
Rama ze ściągiem –
– 7
7
niewiadomych
niewiadomych
P
h
h
2q
M
C
D
E
D
E
q
V
H
D
H
E
V
V
D
H
D
V
E
H
E
26
26
0
:
E
D
H
H
X
0
:
l
q
V
V
Y
E
D
0
2
2
:
l
l
q
l
V
M
E
D
0
2
2
:
l
l
q
M
l
R
h
H
l
V
M
B
E
E
p
C
0
:
P
H
H
H
X
E
D
A
0
2
2
:
l
q
V
V
R
V
Y
E
D
B
A
0
2
2
2
2
:
h
H
h
H
l
V
l
l
q
M
h
P
l
R
M
D
E
E
B
A
l
l
A
B
V
A
H
A
R
B
h
V
D
V
E
l
l
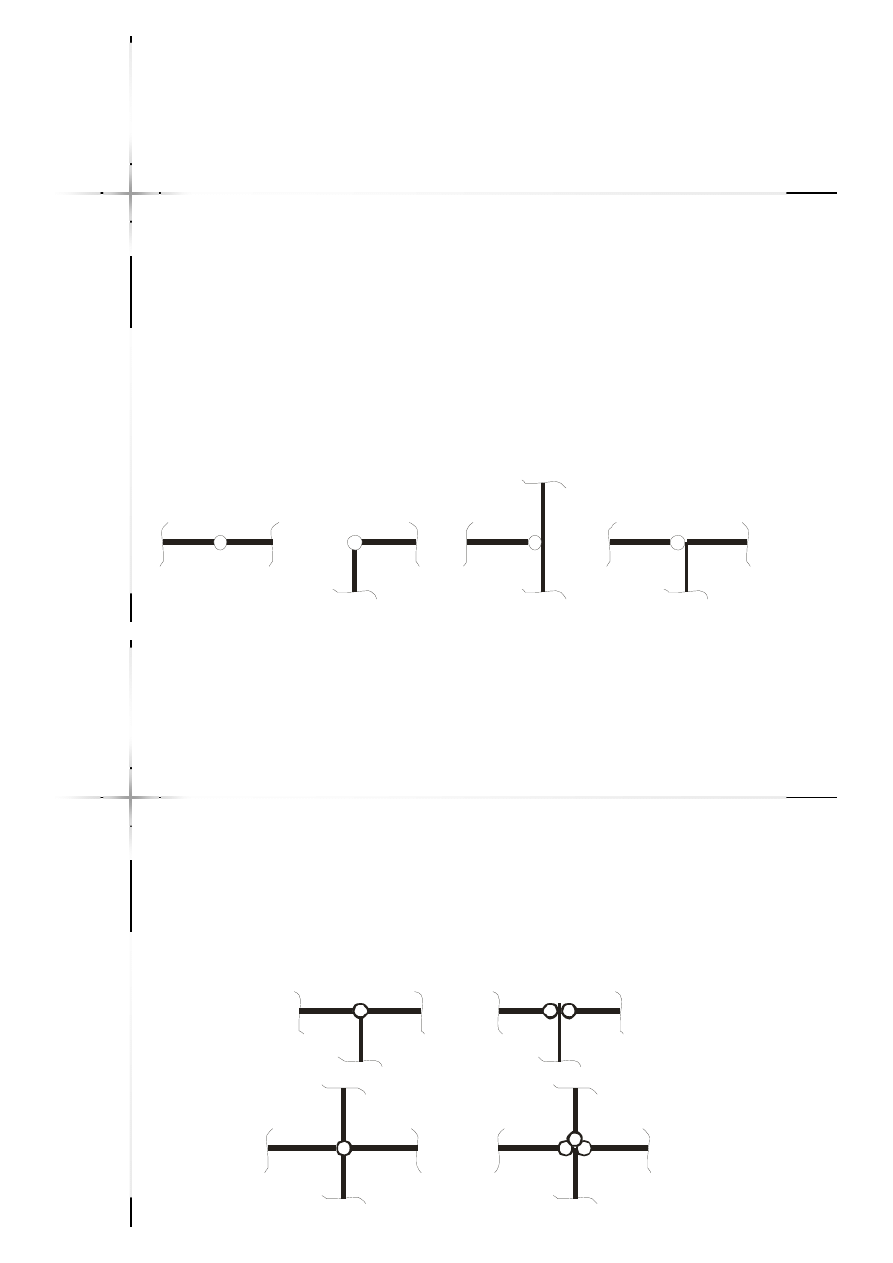
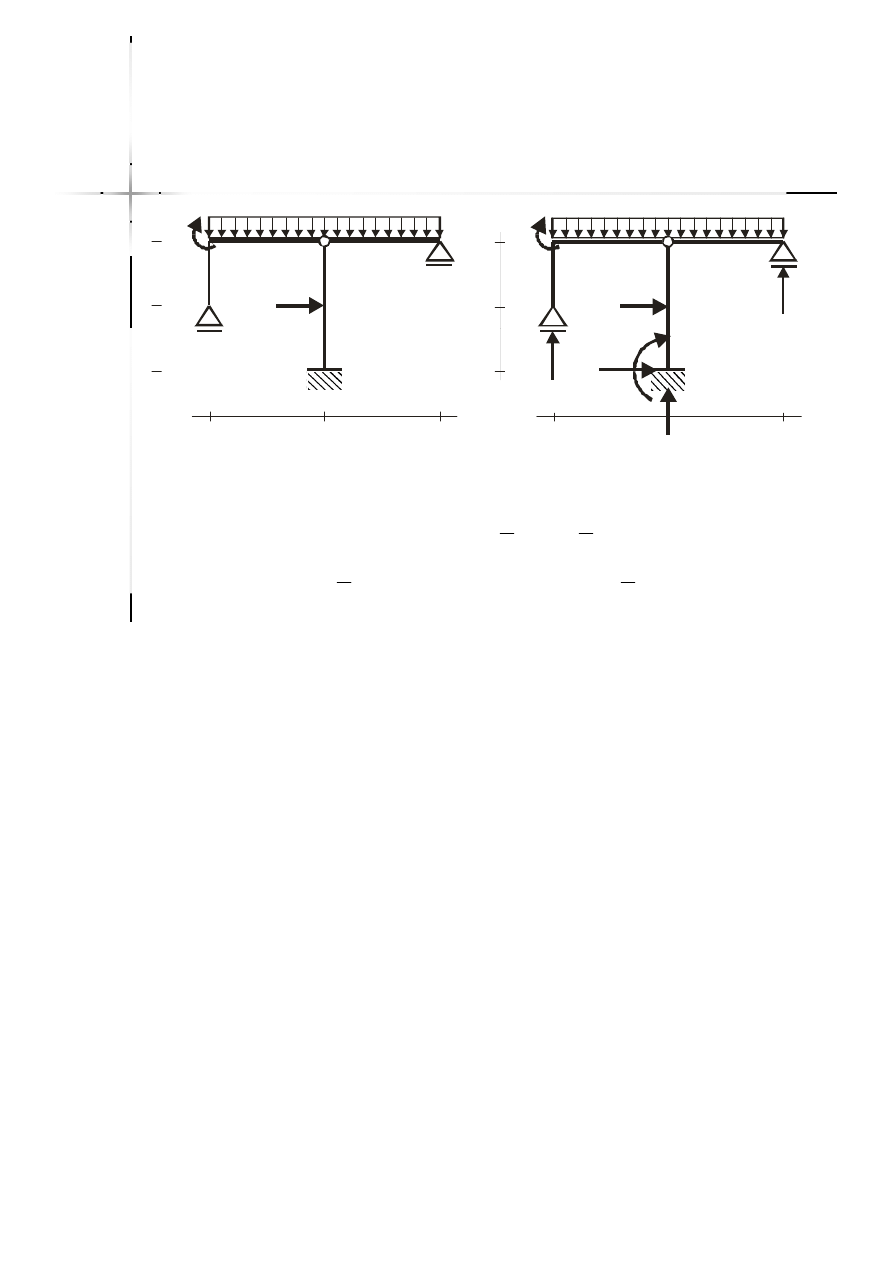
Przeguby pojedyncze
Przeguby pojedyncze
Przeguby, w których jeden pręt łączy
Przeguby, w których jeden pręt łączy
się z drugim ze swobodą obrotu.
się z drugim ze swobodą obrotu.
Pozwala na zapisanie jednego
Pozwala na zapisanie jednego
dodatkowego równania (sumy
dodatkowego równania (sumy
27
27
Pozwala na zapisanie jednego
Pozwala na zapisanie jednego
dodatkowego równania (sumy
dodatkowego równania (sumy
momentów względem przegubu od sił
momentów względem przegubu od sił
na jednej części konstrukcji
na jednej części konstrukcji
oddzielonej przegubem).
oddzielonej przegubem).
Przeguby wielokrotne
Przeguby wielokrotne
Przeguby, w których łączą się ze sobą
Przeguby, w których łączą się ze sobą
więcej niż dwa pręty ze swobodą obrotu
więcej niż dwa pręty ze swobodą obrotu
względem pozostałych prętów.
względem pozostałych prętów.
Pozwalają na zapisanie więcej niż jednego
Pozwalają na zapisanie więcej niż jednego
dodatkowego równania równowagi.
dodatkowego równania równowagi.
28
28
Pozwalają na zapisanie więcej niż jednego
Pozwalają na zapisanie więcej niż jednego
dodatkowego równania równowagi.
dodatkowego równania równowagi.
Rama z przegubem
Rama z przegubem
dwukrotnym
dwukrotnym
M
q
P
h
h
M
q
P
h
h
R
C
M
D
29
29
0
2
:
l
l
q
l
R
M
C
p
D
0
:
P
H
X
B
0
2
:
l
q
R
V
R
Y
C
B
A
0
2
2
:
h
P
l
l
q
l
l
q
M
l
R
M
l
R
M
C
B
A
B
0
2
:
M
l
l
q
l
R
M
A
l
D
h
l
l
h
l
l
R
A
V
B
H
B
M
B
Wyszukiwarka
Podobne podstrony:
5366 Ref 22 id 41421 Nieznany (2)
G2 PB 02 B Rys 3 22 id 185421 Nieznany
IMG 22 id 210963 Nieznany
23 Rozdziae 22 id 30122 Nieznany (2)
PR ETI W 22 1 id 382134 Nieznany
mikro 22 id 300571 Nieznany
IMG 22 id 211205 Nieznany
6 22 id 43144 Nieznany
3 22 id 32895 Nieznany (2)
IMG 22 id 211227 Nieznany
5366 Ref 22 id 41421 Nieznany (2)
G2 PB 02 B Rys 3 22 id 185421 Nieznany
Cwicz 22 2 instrukcja id 124025 Nieznany
Egzamin 22 06 2013 id 151910 Nieznany
Cwicz 22 2 instrukcja id 124025 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
więcej podobnych podstron