3. NOŚNOŚĆ PODŁOŻA GRUNTOWEGO
POD FUNDAMENTAMI BEZPOŚREDNIMI
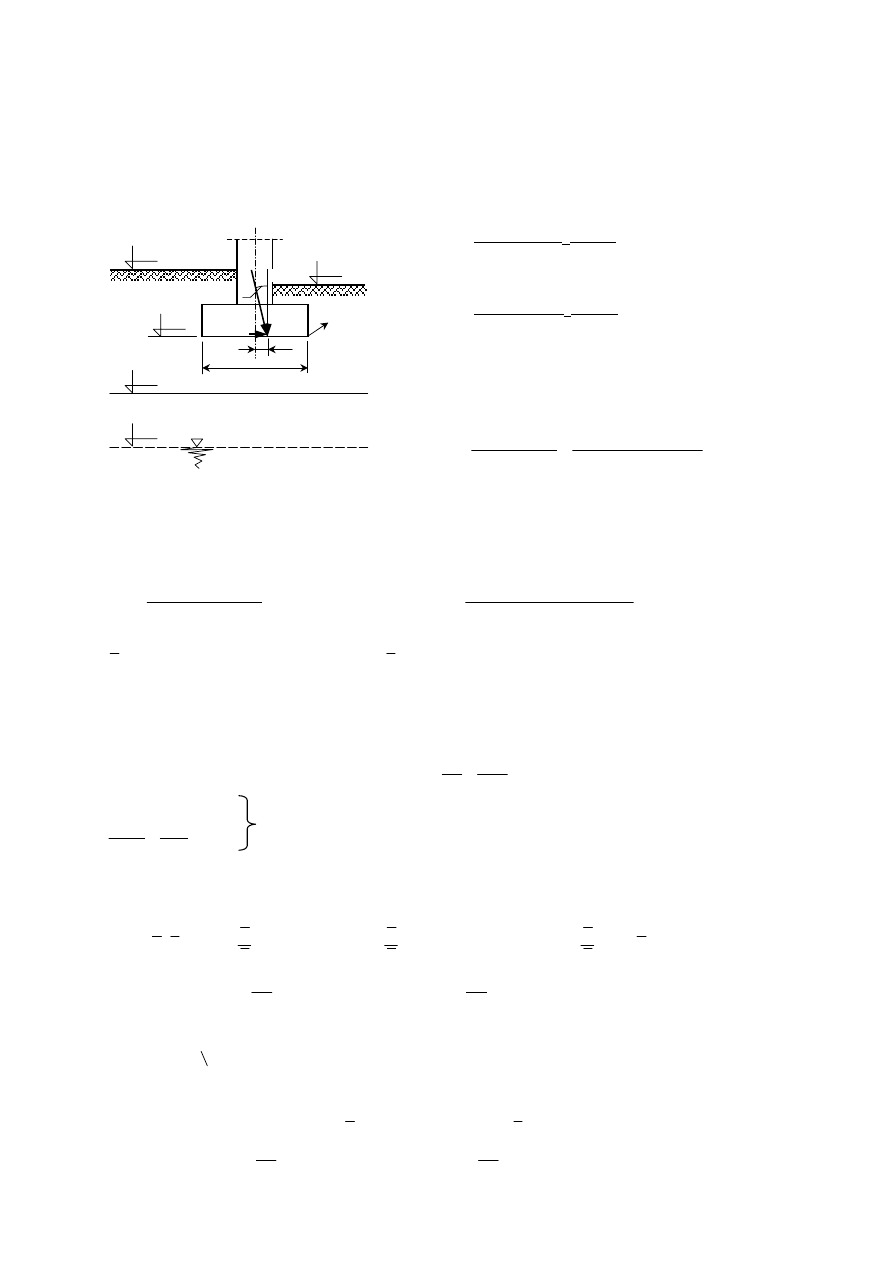
Zadanie przykładowe nr 3.1.
Sprawdzić warunek nośności pionowej podłoża gruntowego pod fundamentem przedstawionym na
rysunku poniżej.
1. Wyznaczenie parametrów geotechnicznych podłoża
gruntowego metodą B, wg PN-81/B-03020
a) warstwa Ps, I
D
= 0.55
φ
(n)
= 33
°, wartość oblicz.
φ
(r)
= 0.9
⋅33 = 29.7°
γ
(n)
= 16.7 kN/m
3
,
γ
(r)
= 0.9
⋅16.7 = 15.0 kN/m
3
,
b) warstwa Pd, I
D
= 0.60
φ
(n)
= 31
°,
φ
(r)
= 0.9
⋅31 = 27.9°
nad wodą (piasek wilgotny):
w = 16%,
γ
(n)
= 17.2 kN/m
3
,
γ
(r)
= 0.9
⋅17.2 = 15.5 kN/m
3
,
pod wodą (piasek nawodniony):
w = 24%,
γ
(n)
= 18.6 kN/m
3
,
γ
s
(n)
= 26.0 kN/m
3
,
42
0
24
0
1
0
26
6
18
24
0
1
0
26
1
1
.
)
.
(
.
.
)
.
(
.
)
w
(
)
w
(
n
s
s
=
+
⋅
−
+
⋅
=
+
−
+
⋅
=
γ
γ
γ
3
9
0
10
0
26
42
0
1
1
.
)
.
.
)(
.
(
)
)(
n
(
w
s
=
−
−
=
−
−
=
′
γ
γ
γ
kN/m
3
γ
’
(r)
= 0.9
⋅ 9.3 = 8.4 kN/m
3
2. Średnie ważone parametry do głębokości 2B
Ze względu na uwarstwioną budowę podłoża gruntowego, z warstw o zbliżonych parametrach, zastąpiono je
podłożem jednorodnym o średnich ważonych parametrach, obliczonych do głębokości 2B.
°
=
⋅
+
⋅
=
6
28
0
3
8
1
9
27
2
1
7
29
.
.
.
.
.
.
)
r
(
φ
=
φ
B
(r)
,
5
12
0
3
2
1
4
8
6
0
5
15
2
1
0
15
.
.
.
.
.
.
.
.
)
r
(
=
⋅
+
⋅
+
⋅
=
γ
kN/m
3
=
γ
B
(r)
3. Zredukowane wymiary fundamentu
2
.
1
15
.
0
2
5
.
1
2
=
⋅
−
=
−
=
B
E
B
B
m,
6
.
2
20
.
0
2
0
.
3
2
=
⋅
−
=
−
=
L
E
L
L
m
4. Współczynniki nośności
dla
φ
B
(r)
= 28.6
° odczytano z nomogramów w PN-81/B-02482 : N
D
= 15.8, N
c
= 27.0, N
B
= 6.0
5. Współczynniki wpływu nachylenia wypadkowej obciążeń Q
r
kąt odchylenia wypadkowej obciążeń od pionu:
15
.
0
1000
150 =
=
=
r
r
N
T
tg
δ
→
δ = 8.5° < φ
B
(r)
= 28.6
°
55
.
0
6
.
28
)
(
=
°
= tg
tg
r
B
φ
27
.
0
55
.
0
15
.
0
)
(
=
=
r
B
tg
tg
φ
δ
6. Zagłębienie minimalne fundamentu: D
min
= 0.8 m,
γ
D
(r)
= 15.0 kN/m
3
7. Opór graniczny podłoża gruntowego:
0
.
880
56
.
0
5
.
12
2
.
1
0
.
6
6
.
2
2
.
1
25
.
0
1
74
.
0
0
.
15
8
.
0
8
.
15
6
.
2
2
.
1
5
.
1
1
6
.
2
2
.
1
25
.
0
1
5
.
1
1
3
.
0
1
)
(
)
(
min
)
(
=
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⋅
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛ −
+
⋅
⋅
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
=
=
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⋅
⋅
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
⋅
⋅
⋅
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
⋅
⋅
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⋅
⋅
=
B
r
B
B
D
r
D
D
c
r
c
fNB
i
B
N
L
B
i
D
N
L
B
i
c
N
L
B
L
B
Q
γ
γ
8. Warunek nośności:
N
r
= 1000 kN
≤ m
⋅Q
fNB
= 0.9
⋅0.9⋅880.0 = 713.0 kN → warunek nie jest spełniony, należy zwiększyć wymiary
fundamentu
9. Sprawdzenie nośności dla fundamentu o zwiększonych wymiarach:
Przyjęto: B = 1.8 m, L = 3.4 m
→
5
.
1
15
.
0
2
8
.
1
=
⋅
−
=
B
m,
0
.
3
20
.
0
2
4
.
3
=
⋅
−
=
L
m
0
.
1353
56
.
0
5
.
12
5
.
1
0
.
6
0
.
3
5
.
1
25
.
0
1
74
.
0
0
.
15
8
.
0
8
.
15
0
.
3
5
.
1
5
.
1
1
0
.
3
5
.
1
=
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⋅
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛ −
+
⋅
⋅
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛ +
⋅
⋅
=
fNB
Q
N
r
= 1000 kN <
m
⋅Q
fNB
= 0.9
⋅0.9⋅1353.0 = 1096.0 kN → warunek nośności spełniony
B = 1.5m
Q
r
N
r
T
r
E
B
L = 3.0m
+ 1.1
0.0
– 1.2
– 1.8
zwg
+ 0.8
Ps, I
D
= 0.55
Pd, I
D
= 0.60
δ
N
r
= 1000 kN
T
r
= 150 kN
E
B
= 0.15 m
E
L
= 0.20 m
kN
z nomogramów wg PN-81/B-02482: i
B
= 0.56, i
D
= 0.74, i
c
= 0.72
(uwaga: dla
δ = 0 → i
B
= i
D
= i
c
= 1.0)
kN
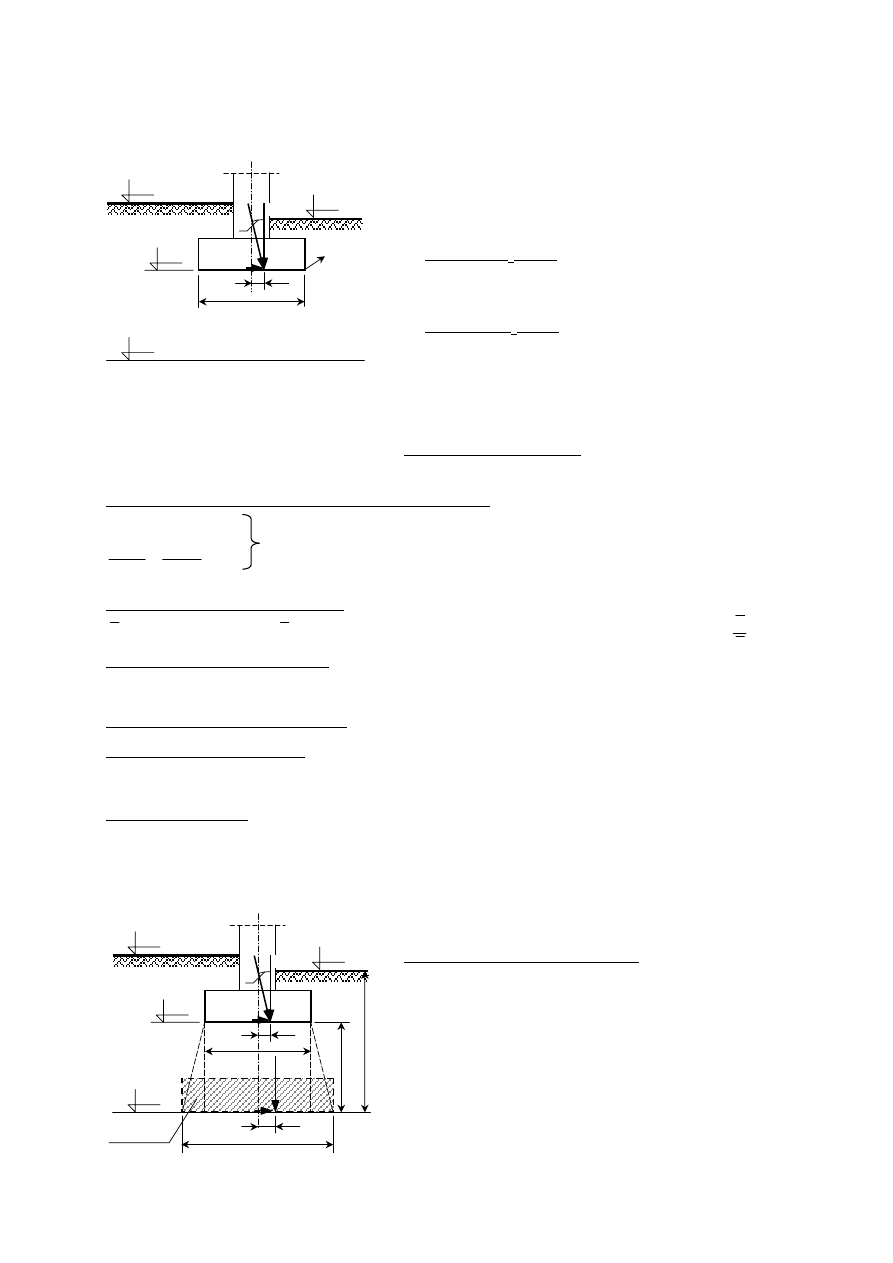
Zadanie przykładowe nr 3.2.
Sprawdzić warunek nośności pionowej podłoża gruntowego pod ławą fundamentową,
przedstawioną na rysunku poniżej.
Ze względu na uwarstwienie podłoża gruntowego oraz
stosunkowo niskie parametry drugiej warstwy G
π, należy
dokonać oddzielnego sprawdzenia nośności dla warstwy Pd i dla
warstwy G
π.
1. Wyznaczenie obliczeniowych parametrów geotechnicznych
podłoża gruntowego
a) warstwa Pd, I
D
= 0.50
φ
(r)
= 0.9
⋅32 = 28.8°
γ
(r)
min
= 0.9
⋅16.5 = 14.85 kN/m
3
,
γ
(r)
max
= 1.1
⋅16.5 = 18.15 kN/m
3
b) warstwa G
π, I
L
= 0.40
φ
(r)
= 0.9
⋅11.5 = 10.35°
c
(r)
= 0.9
⋅10 = 9.0 kPa
γ
(r)
min
= 0.9
⋅ 18.5 = 16.65 kN/m
3
2. Sprawdzenie nośności warstwy pierwszej (Pd)
2.1. Współczynniki nośności:
dla
φ
B
(r)
= 28.8
° → N
D
= 16.1, N
B
= 6.2
2.2. Współczynniki wpływu nachylenia wypadkowej obciążeń :
55
.
0
8
.
28
)
(
=
°
= tg
tg
r
B
φ
24
.
0
55
.
0
5
.
7
)
(
=
°
=
tg
tg
tg
r
B
φ
δ
2.3 Zredukowane wymiary fundamentu
0
.
1
20
.
0
2
4
.
1
=
⋅
−
=
B
m,
0
.
1
=
L
m (ława) , dla ławy o L > 5B we wzorze na Q
fNB
przyjmuje się
0
=
L
B
2.4. Składowe wypadkowej obciążeń
N
r
= Q
r
⋅cos
δ = 125⋅cos7.5° = 124.0 kN/mb, T
r
= Q
r
⋅sin
δ = 125⋅sin7.5° = 16.3 kN/mb
2.5. Zagłębienie minimalne fundamentu: D
min
= 0.5 m,
γ
D
(r)
= 14.85 kN/m
3
2.6. Opór graniczny warstwy Pd:
(
)
(
)
[
]
7
.
156
66
.
0
85
.
14
0
.
1
23
.
6
0
25
.
0
1
80
.
0
85
.
14
5
.
0
1
.
16
0
5
.
1
1
0
.
1
0
.
1
=
⋅
⋅
⋅
⋅
⋅
−
+
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
=
fNB
Q
kN/mb
2.7. Warunek nośności:
N
r
= 124.0 kN/mb < m
⋅Q
fNB
= 0.9
⋅156.7 = 141.0 kN/mb → warunek spełniony
3. Sprawdzenie nośności warstwy drugiej (G
π)
Sprawdzenia nośności drugiej warstwy dokonuje się dla fundamentu
zastępczego, spoczywającego na stropie warstwy drugiej (rys. obok).
3.1. Wymiary fundamentu zastępczego
B’ = B + b, L’ = L + b, (dla ławy L’ = L = 1.0 mb)
- dla warstwy 1 z gruntu niespoistego : przy h
≤ B → b = h/3
przy h > B
→ b = 2/3h
- dla warstwy 1 z gruntu spoistego : przy h
≤ B → b = h/4
przy h > B
→ b = h/3
przy h > 2B – nośności drugiej warstwy można nie sprawdzać
W zadaniu:
warstwa 1 – grunt niespoisty, h = 1.6 m > B
→ b = 2/3⋅1.6 = 1.07 m
B’ = 1.4 + 1.07 = 2.47 m, L’ = L = 1.0 mb
B = 1.4m
Q
r
N
r
T
r
E
B
Ława
L > 5B
+ 0.9
0.0
– 1.6
+ 0.5
Pd, I
D
= 0.50
φ
(n)
= 32
°, c = 0.0
γ
(n)
= 16.5 kN/m
3
G
π, I
L
= 0.40, gen. C
φ
(n)
= 11.5
°, c
(n)
= 10 kPa
γ
(n)
= 18.5 kN/m
3
δ
Q
r
= 125 kN/m
δ = 7.5°
E
B
= 0.20 m
→ i
D
= 0.80, i
B
= 0.66
B = 1.4m
Q
r
N
r
T
r
E
B
+ 0.9
0.0
– 1.6
+ 0.5
warstwa 1
Pd, I
D
= 0.50
warstwa 2
G
π, I
L
= 0.40
δ
B’ = B+b
N
r
’
E’
B
T
r
’
h
fundament
zastępczy
D’
min
3.2. Obciążenia fundamentu zastępczego i mimośrody:
N
r
’ = N
r
+ B’
⋅L’⋅h⋅
γ
1
(r)
max
= 124.0 + 2.47
⋅1.0⋅1.6⋅18.15 = 195.7 kN/m,
T
r
’ = T
r
= 16.3 kN/mb (brak dodatkowych obciążeń poziomych)
26
.
0
7
.
195
6
.
1
3
.
16
2
.
0
0
.
124
=
⋅
+
⋅
=
′
⋅
±
⋅
=
′
r
rB
B
r
B
N
h
T
E
N
E
m,
0
.
0
=
′
⋅
±
⋅
=
′
r
rL
L
r
L
N
h
T
E
N
E
m
3.3. Współczynniki nośności:
dla
φ
B
(r)
= 10.35
° → N
c
= 8.5, N
D
= 2.52, N
B
= 0.21
3.4. Zredukowane wymiary fundamentu zastępczego :
95
.
1
26
.
0
2
47
.
2
=
⋅
−
=
′
B
m,
0
.
1
=
′
L
m
3.5. Współczynniki wpływu nachylenia wypadkowej obciążeń :
W przypadku gruntu spoistego należy obliczyć zastępczy kąt pochylenia wypadkowej obciążeń:
0559
.
0
0
.
1
95
.
1
35
.
10
0
.
9
7
.
195
3
.
16
)
(
)
(
*
=
⋅
⋅
°
⋅
+
=
⋅
⋅
⋅
+
=
ctg
L
B
ctg
c
N
T
tg
r
B
r
r
r
φ
δ
→
δ* = 3.2° < φ
B
(r)
= 10.35
°
(w powyższym wzorze wstawiono wielkości dla fundamentu zastępczego:
r
r
T
L
B
N
′
′
′
′
,
,
,
)
18
.
0
35
.
10
)
(
=
°
= tg
tg
r
B
φ
31
.
0
18
.
0
0559
.
0
)
(
*
=
=
r
B
tg
tg
φ
δ
3.6. Zagłębienie minimalne fundamentu zastępczego: D’
min
= 0.5 + 1.6 = 2.1 m,
γ
D
(r)
= 14.85 kN/m
3
3.7. Opór graniczny warstwy G
π:
[
]
0
.
287
82
.
0
65
.
16
95
.
1
21
.
0
0
.
1
95
.
0
85
.
14
1
.
2
52
.
2
0
.
1
88
.
0
0
.
9
5
.
8
0
.
1
0
.
1
95
.
1
=
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
=
′
fNB
Q
kN/mb
3.7. Warunek nośności:
N
r
’ = 195.7 kN/mb < m
⋅Q’
fNB
= 0.9
⋅287.0 = 258.3 kN/mb → warunek spełniony
Wniosek końcowy:
Nośność pionowa uwarstwionego podłoża gruntowego pod zadanym fundamentem jest wystarczająca.
→ i
c
= 0.88, i
D
= 0.95, i
B
= 0.82
Nomogramy i materiały pomocnicze
fNB
r
Q
m
N
⋅
≤
⎥⎦
⎤
⎢⎣
⎡
⋅
⋅
⋅
⋅
−
+
⋅
⋅
⋅
⋅
+
+
⋅
⋅
⋅
+
⋅
⋅
=
B
r
B
B
D
r
D
D
c
r
C
fNB
i
B
N
L
B
i
D
N
L
B
i
c
N
L
B
L
B
Q
)
(
min
)
(
)
(
)
25
.
0
1
(
)
5
.
1
1
(
)
3
.
0
1
(
γ
γ
gdzie:
L
B
E
L
L
E
B
B
L
B
≤
−
=
−
=
,
2
,
2
Dla ław fundamentowych przyjmuje się:
r
N
[kN/m],
0
,
1
=
=
L
B
mb
L
)
2
4
(
2
φ
π
φ
π
+
⋅
=
tg
e
N
tg
D
φ
ctg
N
N
D
C
⋅
−
=
)
1
(
φ
tg
N
N
D
B
⋅
−
⋅
=
)
1
(
75
.
0
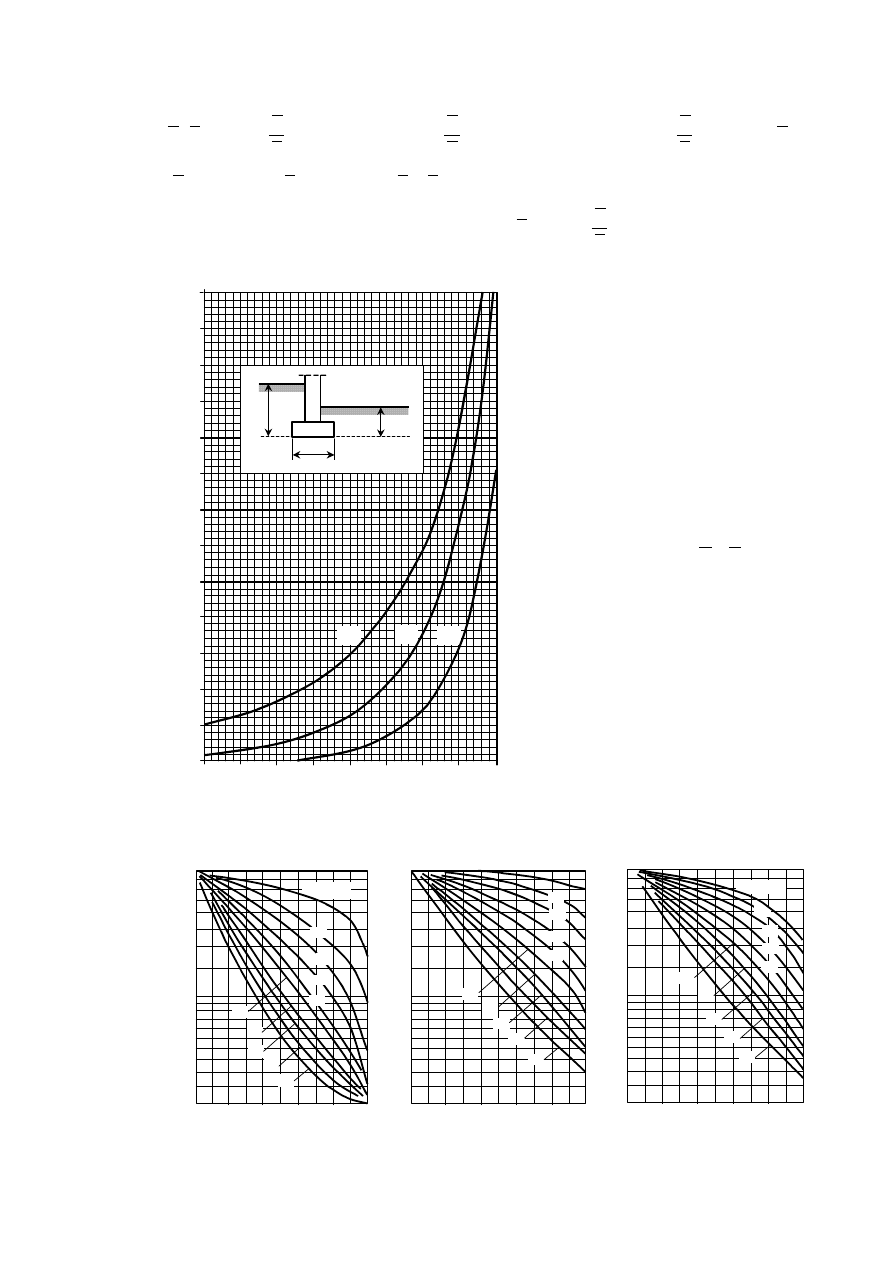
Rys. 9.1. Nomogram do wyznaczania współczynników nośności N
C
, N
D
i N
B
według PN-81/B-03020
Rys. 9.2. Nomogramy do wyznaczania współczynników redukcyjnych „i” według PN-81/B-03020
0
°
0
N
D
N
B
5
10
15
20
25
30
35
40
45
50
55
60
N
φ
(r)
5
° 10° 15° 20° 25°
30
°
35
°
B
D
D
min
γ
D
γ
B
N
C
1.0
0.8
0.6
0.5
0.4
0.3
0.2
0.1
0.2
0 0.4
0.6
0.8
1.0
tg
δ/tgφ
(r)
i
B
tg
φ
(r)
=0.1
0.6
0.7
0.8
0.9
1.0
0.4
0.2
0.3
0.5
1.0
0.8
0.6
0.5
0.4
0.3
0.2
0.1
0.2
0 0.4
0.6
0.8
1.0
tg
δ/tgφ
(r)
i
D
tg
φ
(r)
=0.1
0.6
0.7
0.8
0.9
1.0
0.2
0.3
0.4
0.5
1.0
0.8
0.6
0.5
0.4
0.3
0.2
0.1
0.2
0 0.4
0.6
0.8
1.0
tg
δ/tgφ
(r)
i
C
tg
φ
(r)
=0.1
0.6
0.7
0.8
0.9
1.0
0.4
0.2
0.5
0.3
