Zad. 1.

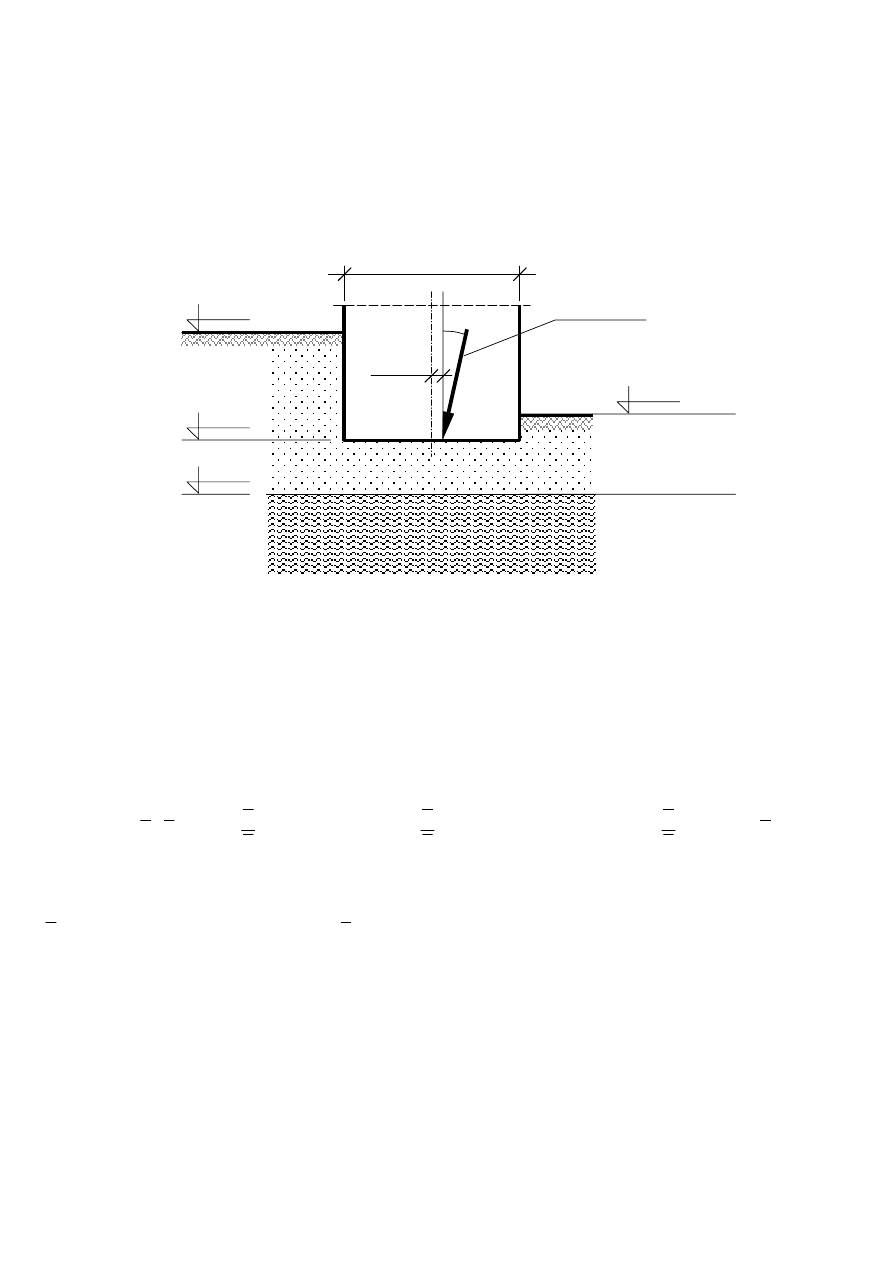
Sprawdzić zgodnie z normą PN-81/B-03020 warunek I-go stanu granicznego (warunek nośności podłoża) dla

podłoża uwarstwionego przedstawionego na rysunku. Parametry geotechniczne podłoża ustalono metoda A

(otrzymane współczynniki materiałowe wynoszą

γ

m

= 0.9). Wymiary fundamentu: B = 2.0 m, L = 4.0 m.

Obliczeniowa siła wypadkowa R

r

= 1460 kN nachylona jest do pionu pod kątem

δ

B

= 6.75

° i działa na

mimośrodzie e

B

= 0.1 m.

Warunek I-go stanu granicznego: N

r

≤ m · Q

fNB

gdzie: N

r

– obliczeniowa wartość pionowej składowej obciążenia [kN],

m – współczynnik korekcyjny ( m = 0.9 dla metody „A” określania parametrów gruntowych,

m = 0.9 · 0.9 dla metody „B” określania parametrów gruntowych),

Q

fNB

– pionowa składowa obliczeniowego oporu granicznego podłoża gruntowego [kN],

obliczona wg wzoru:

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⋅

γ

⋅

⎟

⎠

⎞

⎜

⎝

⎛ −

+

⋅

⋅

γ

⋅

⎟

⎠

⎞

⎜

⎝

⎛ +

+

⋅

⋅

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

=

B

)

r

(
B

B

D

min

)

r

(
D

D

c

)

r

(
u

c

fNB

i

B

N

L

B

25

.

0

1

i

D

N

L

B

5

.

1

1

i

c

N

L

B

3

.

0

1

L

B

Q

Szerokość i długość z uwzględnieniem mimośrodów:

m

8

.

1

m

1

.

0

2

m

0

.

2

e

2

B

B

B

=

⋅

−

=

−

=

,

m

0

.

4

0

m

0

.

4

e

2

L

L

L

=

−

=

−

=

e

B

, e

L

– mimośrody działania obciążenia w kier. równoległym do szerokości i długości podstawy fundamentu,

D

min

= 0.5 m – głębokość posadowienia, mierzona do najniższego poziomu terenu (np. podłogi piwnicy),

φ

u

(r)

– obliczeniowa wartość kąta tarcia wewnętrznego gruntu zalegającego bezpośrednio poniżej poziomu

posadowienia [

°],

c

u

(r)

– obliczeniowa wartość spójności gruntu zalegającego bezpośrednio poniżej poziomu posadowienia [kPa],

γ

D

(r)

– obliczeniowy ciężar objętościowy gruntu zalegającego powyżej poziomu posadowienia [kN/m

3

],

γ

B

(r)

– obliczeniowy ciężar objętościowy gruntu zalegającego bezpośrednio poniżej poziomu posad. [kN/m

3

],

B= 2.0 m

Piasek drobny, I

D

= 0.6

φ

(n)

= 31

°

γ

(n)

= 16.18 kN/m

3

+ 2.0

e

B

= 0.10 m

R

r

= 1460 kN

+ 0.5

± 0.0

Ił pylasty, I

L

= 0.4

φ

(n)

= 7.5

°

c

(n)

= 39.22 kPa

γ

(n)

= 18.14 kN/m

3

- 1.0

δ

B

= 6.75

°

Dla piasku drobnego:

φ

u

(r)

=

φ

u

(n)

·

γ

m

= 31

° · 0.9 = 27.9°

γ

D

(r)

=

γ

B

(r)

=

γ

(n)

·

γ

m

= 16.18 kN/m

3

· 0.9 = 14.56 kN/m

3

Dla iłu pylastego:

φ

u

(r)

=

φ

u

(n)

·

γ

m

= 7.5

° · 0.9 = 6.75°

c

u

(r)

= c

u

(n)

·

γ

m

= 39.22 · 0.9 = 35.30 kPa

γ

B

(r)

=

γ

(n)

·

γ

m

= 18.14 kN/m

3

· 0.9 = 16.32 kN/m

3

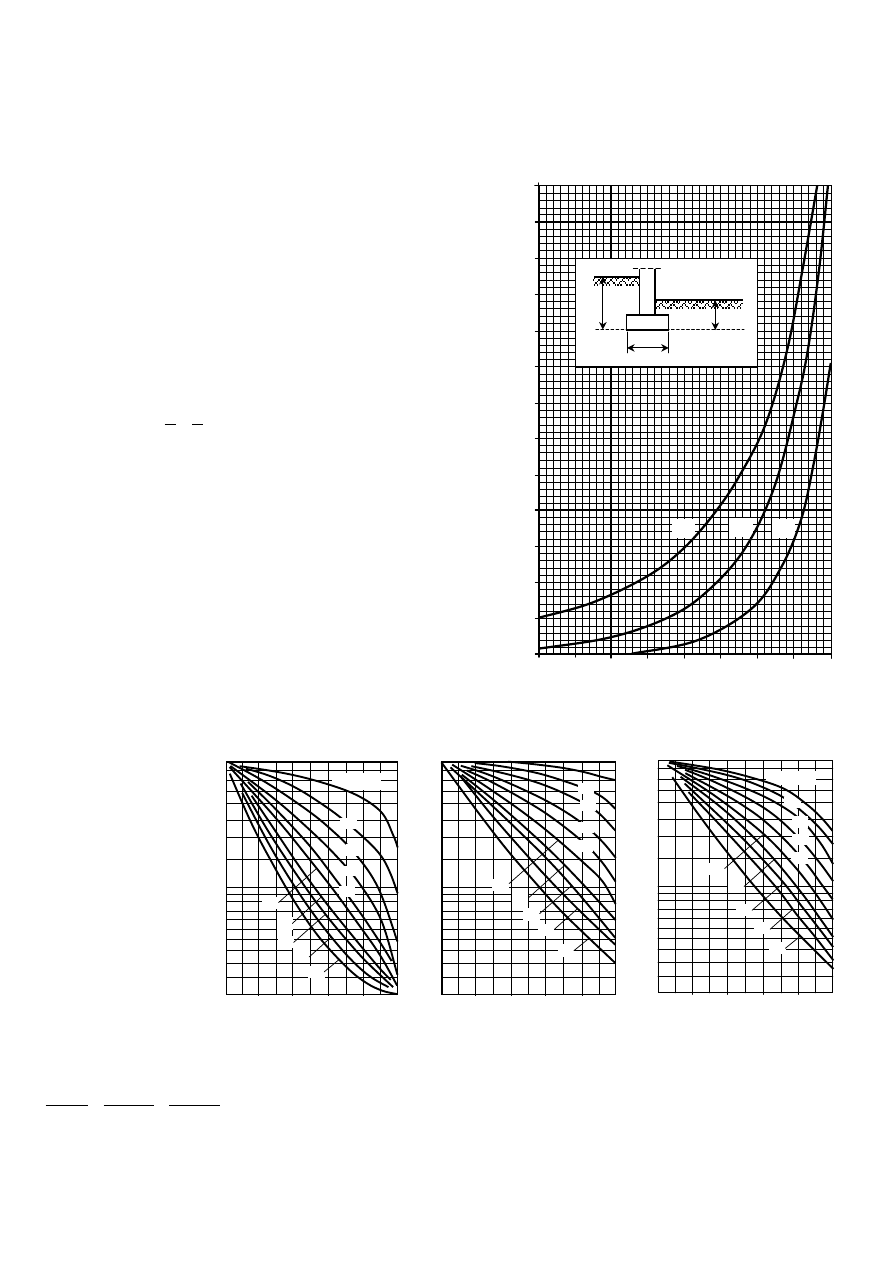
N

c

, N

D

, N

B

– współczynniki nośności

przyjmowane wg wzorów lub wykresu:

⎟

⎠

⎞

⎜

⎝

⎛

φ

+

π

=

φ

π

2

4

tg

N

2

tg

D

)

r

(

e

,

φ

−

=

ctg

)

1

N

(

N

D

C

,

φ

−

=

tg

)

1

N

(

75

.

0

N

D

B

Dla piasku (

φ

u

(r)

= 27.9

°):

N

D

= 14.6, N

B

= 5.4

Dla iłu pylastego (

φ

u

(r)

= 6.75

°):

N

c

= 7.07, N

D

= 1.84, N

B

= 0.08

i

c

, i

D

, i

B

– współczynniki wpływu nachylenia wypadkowej obciążenia przyjmowane z nomogramów:

dla:

62

.

0

i

,

85

.

0

i

5294

.

0

tg

2235

.

0

5294

.

0

1183

.

0

9

.

27

tg

75

.

6

tg

tg

tg

B

D

)

r

(
u

)

r

(
u

B

=

=

⇒

⎪

⎭

⎪

⎬

⎫

=

φ

=

=

=

φ

δ

0

°

0

N

D

N

B

5

10

15

20

25

30

35

40

45

50

55

60

N

φ

(r)

5

°

10

°

15

° 20° 25° 30°

35

°

B

D

D

min

γ

D

γ

B

N

C

1.0

0.8

0.6

0.5

0.4

0.3

0.2

0.1

0.2

0 0.4

0.6

0.8

1.0

tg

δ/tgφ

(r)

i

B

tg

φ

(r)

=0.1

0.6

0.7

0.8

0.9

1.0

0.4

0.2

0.3

0.5

1.0

0.8

0.6

0.5

0.4

0.3

0.2

0.1

0.2

0

0.4

0.6

0.8

1.0

tg

δ/tgφ

(r)

i

D

tg

φ

(r)

=0.1

0.6

0.7

0.8

0.9

1.0

0.2

0.3

0.4

0.5

1.0

0.8

0.6

0.5

0.4

0.3

0.2

0.1

0.2

0 0.4

0.6

0.8

1.0

tg

δ/tgφ

(r)

i

C

tg

φ

(r)

=0.1

0.6

0.7

0.8

0.9

1.0

0.4

0.2

0.5

0.3

A. Sprawdzenie warunku I-go stanu granicznego w poziomie posadowienia

Obliczeniowa wartość pionowej składowej obciążenia: N

r

= R

r

· cos

δ

B

= 1460 kN · cos 6.75

° = 1450 kN

kN

2

.

1650

Q

62

.

0

m

8

.

1

m

kN

56

.

14

4

.

5

m

0

.

4

m

8

.

1

25

.

0

1

85

.

0

m

5

.

0

m

kN

56

.

14

6

.

14

m

0

.

4

m

8

.

1

5

.

1

1

m

0

.

4

m

8

.

1

Q

fNB

3

3

fNB

=

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⋅

⋅

⎟

⎠

⎞

⎜

⎝

⎛ −

+

⋅

⋅

⋅

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

=

N

r

≤ m · Q

fNB

1450 kN < 0.9 · 1650.2 = 1485.2 kN

warunek w poziomie posadowienia jest spełniony.

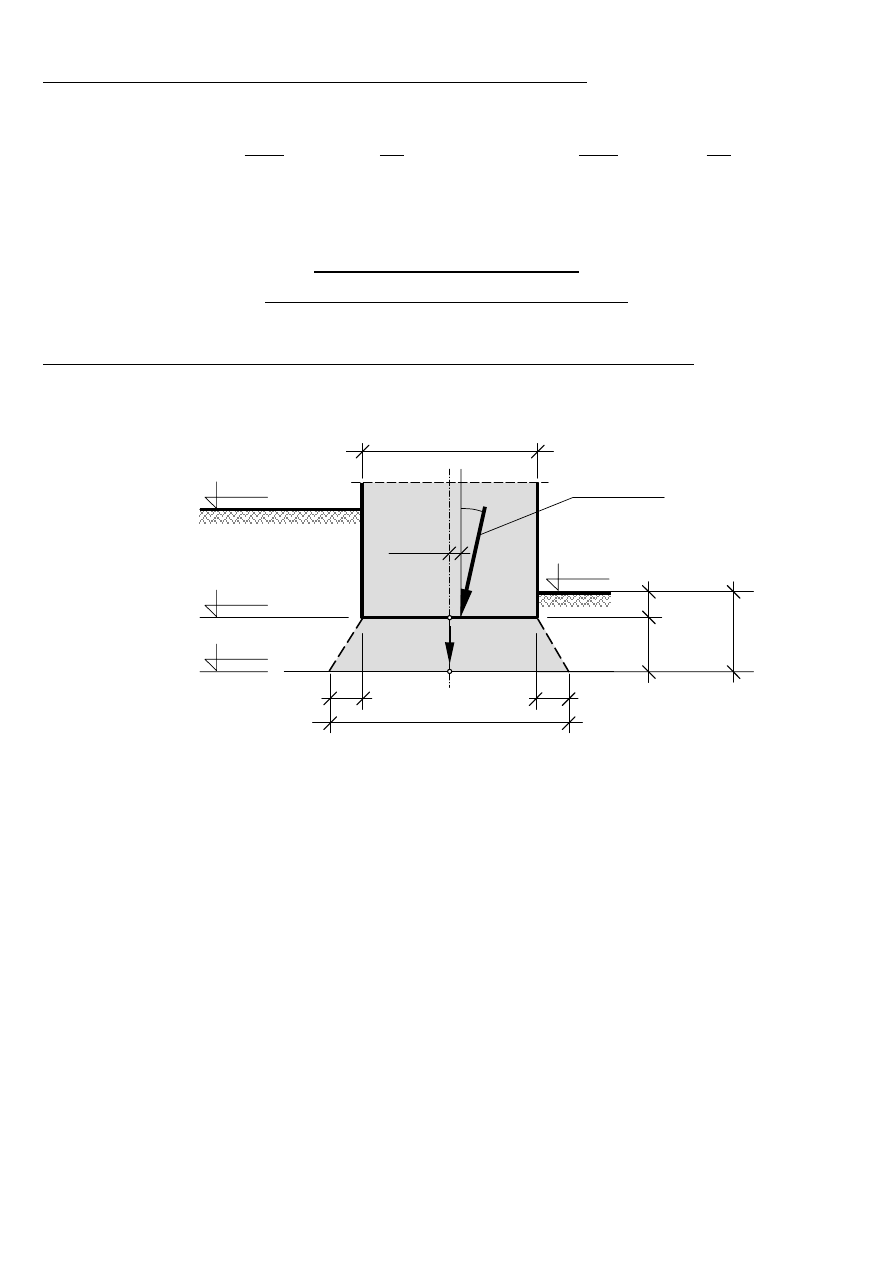
B. Sprawdzenie warunku I-go stanu granicznego w poziomie stropu warstwy iłu pylastego

Do sprawdzenia warunku wykorzystuje się metodę „fundamentu zastępczego” o szerokości B’ posadowionego

na głębokości D’

min

= D

min

+ h:

Wymiary podstawy fundamentu zastępczego zwiększamy o wartość b w zależności od odległości stropu

sprawdzanej od poziomu fundamentu oraz rodzaju gruntu:

dla gruntów spoistych:

przy h

≤ B → b = h/4

przy h > B

→ b = h/3

dla gruntów niespoistych: przy h

≤ B → b = h/3

przy h > B

→ b = 2h/3

Dla gruntu niespoistego oraz przy h = 1.0 m < B = 2.0 m wymiary podstawy fundamentu zastępczego

zwiększamy o b = h/3 = 1.0m/3 = 0.333 m:

B’ = B + b = 2.0 m + 0.333 m = 2.333 m

L’ = L + b = 4.0 m + 0.333 m = 4.333 m

Minimalna głębokość posadowienia:

D’

min

= D

min

+ h = 0.5 m + 1.0 m = 1.5 m

Obliczeniowa wartość pionowej składowej obciążenia (zwiększona o ciężar gruntu G):

N

r

’ = Nr + B’ · L’ · h ·

γ

h

(r)

= 1450 kN + 2.333 m · 4.333 m · 1.0 m · 14.56 kN/m

3

= 1597.18 kN

B= 2.0 m

+ 2.0

e

B

= 0.10 m

R

r

= 1460 kN

+ 0.5

± 0.0

- 1.0

δ

B

= 6.75

°

B’ = B +b

b/2 b/2

h = 1.0 m

D

min

= 0.5 m

D’

min

= 1.5 m

0

0’

G

Obliczeniowa wartość poziomej składowej obciążenia:

T

rB

= Nr · tg

δ

B

= 1450 · tg 6.75

° = 171.62 kN

o

13

.

6

'

1074

.

0

kN

18

.

1597

kN

62

.

171

'

N

T

'

tg

B

r

rB

B

=

δ

→

=

=

=

δ

Nowy mimośród obciążenia:

'

N

h

T

e

N

N

M

'

e

r

rB

B

r

'

0

B

⋅

±

⋅

=

=

∑

∑

W niniejszym przypadku moment od siły N

r

kręci w prawo względem 0’ a od siły T

rB

w lewo, stąd:

m

0166

.

0

18

.

1597

0

.

1

62

.

171

1

.

0

1450

'

N

h

T

e

N

'

e

r

rB

B

r

B

−

=

⋅

−

⋅

=

⋅

−

⋅

=

znak „minus” oznacza, że mimośród e

B

’ występuje po lewej stronie środka podstawy fundamentu zastępczego.

Szerokość i długość z uwzględnieniem mimośrodów:

m

3

.

2

m

0166

.

0

2

m

333

.

2

'

e

2

'

B

B

B

=

⋅

−

=

−

=

,

m

333

.

4

'

L

L

=

=

współczynniki wpływu nachylenia wypadkowej obciążenia dla:

5

.

0

i

,

8

.

0

i

,

5

.

0

i

1183

.

0

tg

9074

.

0

75

.

6

tg

13

.

6

tg

tg

tg

B

D

c

)

r

(
u

)

r

(
u

B

=

=

=

⇒

⎪

⎭

⎪

⎬

⎫

=

φ

=

=

φ

δ

kN

1

.

2030

Q

5

.

0

m

3

.

2

m

kN

32

.

16

08

.

0

m

333

.

4

m

3

.

2

25

.

0

1

8

.

0

m

5

.

1

m

kN

56

.

14

84

.

1

m

333

.

4

m

3

.

2

5

.

1

1

5

.

0

kPa

30

.

35

07

.

7

m

333

.

4

m

3

.

2

5

.

1

1

m

333

.

4

m

3

.

2

Q

fNB

3

3

fNB

=

⎥

⎦

⎤

⋅

⋅

⋅

⎟

⎠

⎞

⎜

⎝

⎛ −

+

+

⋅

⋅

⋅

⎟

⎠

⎞

⎜

⎝

⎛ +

+

⎢

⎣

⎡

+

⋅

⋅

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

=

N

r

≤ m · Q

fNB

1597.18 kN < 0.9 · 2030.1 = 1827.1 kN

warunek w poziomie stropu iłu pylastego jest spełniony.

e

B

= 0.10 m

R

r

= 1460 kN

δ

B

= 6.75

°

0

0’

T

rB

N

r

h = 1.0 m

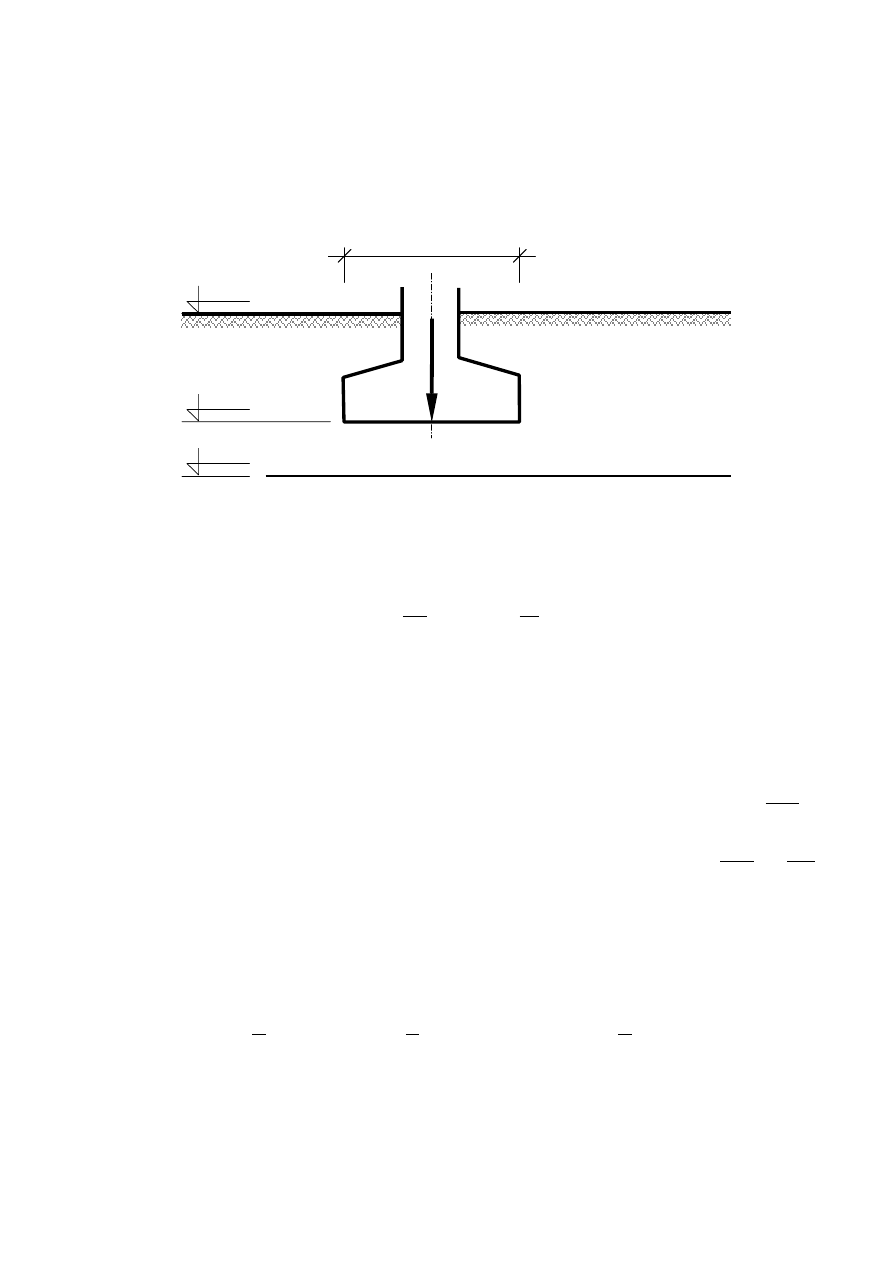
Zad. 2.

Stopa fundamentowa ma wymiary 2.0 × 2.0 m i posadowiona jest poprzez średniozagęszczoną podsypkę

żwirową o miąższości 0.8 m na glinie pylastej. Obliczeniowe pionowe obciążenie osiowe stopy wynosi

N

r

= 2400 kN. Sprawdzić nośność podłoża (dla żwiru i gliny) dla warunków jak na rysunku. Parametry

geotechniczne podłoża ustalono metoda A.

Dla obciążenia pionowego osiowego lub gdy

1

.

0

N

T

r

rB

<

oraz

035

.

0

B

e

B

≤

warunek I-go stanu granicznego

dopuszcza się sprawdzać według wzorów:

q

rs

≤ m · q

f

q

rmax

≤ 1.2 · m · q

f

gdzie: q

rs

– średnie obliczeniowe obciążenie jednostkowe podłoża pod fundamentem [kPa],

L

B

N

q

r

rs

⋅

=

,

q

rmax

– maksymalne obciążenie jednostkowe podłoża pod fundamentem [kPa],

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

=

B

e

6

1

L

B

N

q

B

r

rs

,

m – współczynnik korekcyjny jak w zadaniu 1,

q

f

– obliczeniowy opór jednostkowy jednowarstwowego podłoża pod fundamentem [kPa],

obliczany wg wzoru:

B

N

L

B

25

.

0

1

D

N

L

B

5

.

1

1

c

N

L

B

3

.

0

1

q

)

r

(
B

B

min

)

r

(
D

D

)

r

(
u

c

f

⋅

γ

⋅

⎟

⎠

⎞

⎜

⎝

⎛ −

+

⋅

γ

⋅

⎟

⎠

⎞

⎜

⎝

⎛ +

+

⋅

⎟

⎠

⎞

⎜

⎝

⎛ +

=

Współczynniki nośności:

dla żwiru o kącie tarcia wewnętrznego

φ

(r)

= 35

° → N

D

= 33.3 N

B

= 16.96,

dla gliny pylastej o kącie tarcia

φ

(r)

= 11.25

° → N

c

= 8.63 N

D

= 33.3 N

B

= 16.96,

B= 2.0 m

Żwir,
φ

(r)

= 35

°

γ

(r)

= 16.33 kN/m

3

+ 2.0

N

r

= 2400 kN

± 0.0

Glina pylasta,
φ

(n)

= 11.25

°

c

(n)

= 19.41 kPa

γ

(n)

= 17.65 kN/m

3

- 0.8

Obliczeniowy opór jednostkowy żwiru pod fundamentem:

kPa

39

.

3134

0

.

2

33

.

16

96

.

16

0

.

2

0

.

2

25

.

0

1

0

.

2

33

.

16

3

.

33

0

.

2

0

.

2

5

.

1

1

q

f

=

⋅

⋅

⎟

⎠

⎞

⎜

⎝

⎛ −

+

⋅

⋅

⎟

⎠

⎞

⎜

⎝

⎛ +

=

kPa

600

0

.

2

0

.

2

2400

L

B

N

q

r

rs

=

⋅

=

⋅

=

q

rs

≤ m · q

f

600 kPa < 0.9 · 3134.39 = 2829 kPa

warunek spełniony

Sprawdzenie warunku nośności dla stropu gliny pylastej należy wykonać stosując fundament zastępczy.

Dla gruntu niespoistego ora h < B, b = h/3 = 0.8/3 = 0.267 m

B’ = L’ = 2.0 + 0.267 m

N

r

’ = N

r

+ B’ · L’ · h ·

γ

h

(r)

= 2400 + 2.267 · 2.267 · 0.8 · 16.33 = 2467.17 kN

D’

min

= D

min

+ h = 2.0 + 0.8 = 2.8 m

(

)

(

)

(

)

kPa

48

.

536

267

.

2

65

.

17

26

.

0

25

.

0

1

8

.

2

33

.

16

72

.

2

5

.

1

1

41

.

19

63

.

8

3

.

0

1

q

f

=

⋅

⋅

−

+

⋅

⋅

+

+

⋅

+

=

kPa

05

.

480

267

.

2

267

.

2

14

.

2467

'

L

'

B

'

N

q

r

rs

=

⋅

=

⋅

=

q

rs

≤ m · q

f

480.05 kPa < 0.9 · 536.48 = 482.80 kPa

warunek spełniony