1) Definicja, dziedzina, zbiór wartości, wykres : funkcji wykładniczej i logarytmicznej. 

dziedziną funkcji nazywa się zbiór wszystkich dopuszczalnych argumentów danej 
funkcji, lub – dla funkcji wieloargumentowej – zbiór par, trójek lub ogólnie krotek jej 
argumentów.  
Zbiór wartości to zbiór zawierający wszystkie liczby, które możemy otrzymać ze 
wzoru funkcji wykł:  

, gdzie 

. 



 

podstawa   funkcji wykładniczej była różna od 1, ponieważ dla 

funkcja 

jest 

funkcją stałą. 

 



 

 

 



 

Dla 

funkcja wykładnicza o podstawie   jest rosnąca, dla 

malejąca. 

Jeśli 

to funkcja 

jest stała. 



 

Pochodna funkcji wykładniczej to: 

 

(patrz dowód w logarytm naturalny) 

Czyli w szczególności dla 

 mamy 

 



 

Funkcja wykładnicza o podstawie 

 jest (przy argumencie dążącym do 

) 

asymptotycznie większa niż funkcja wielomianowa, mniejsza zaś niż silnia. 

Funkcja logarytmiczna – funkcja 

, określona wzorem 

(dla pewnego ustalonego 

). Zalicza się ją do funkcji 

elementarnych. Jest funkcją odwrotną do funkcji wykładniczej. 

Często funkcję logarytmiczną nazywa się krótko logarytmem, chociaż są to dwa różne 
pojęcia: logarytm liczby to wartość funkcji logarytmicznej dla ustalonego argumentu. 

Ważną funkcją logarytmiczną jest logarytm naturalny: jest to funkcja pierwotna funkcji 

 

 

 

 
Funkcja logarytmiczna jest 



 

ściśle monotoniczna – dla 

 funkcja ta jest rosnąca, dla 

funkcja jest 

malejąca, 



 

różnowartościowa. 



 

nieograniczona 



 

nieokresowa, 



 

suriekcją, 



 

ciągła, 



 

różniczkowalna, 



 

przestępna. 

Funkcja ta nie jest parzysta ani nieparzysta. 

 
2) Definicja granicy skończonej oraz nieskończonej ciągu (an).  
Def. liczby e , twierdzenie o ciągach zbieżnych do liczby e. 

 

wzór na ciąg zbieżny do liczby e 

 
3) Udowodnić, że dla n= 1,2,...  arg (z)= n arg z ,   z=(przekreślone) (0,0) 

 
 
 
 
 
 
 
 
 
 

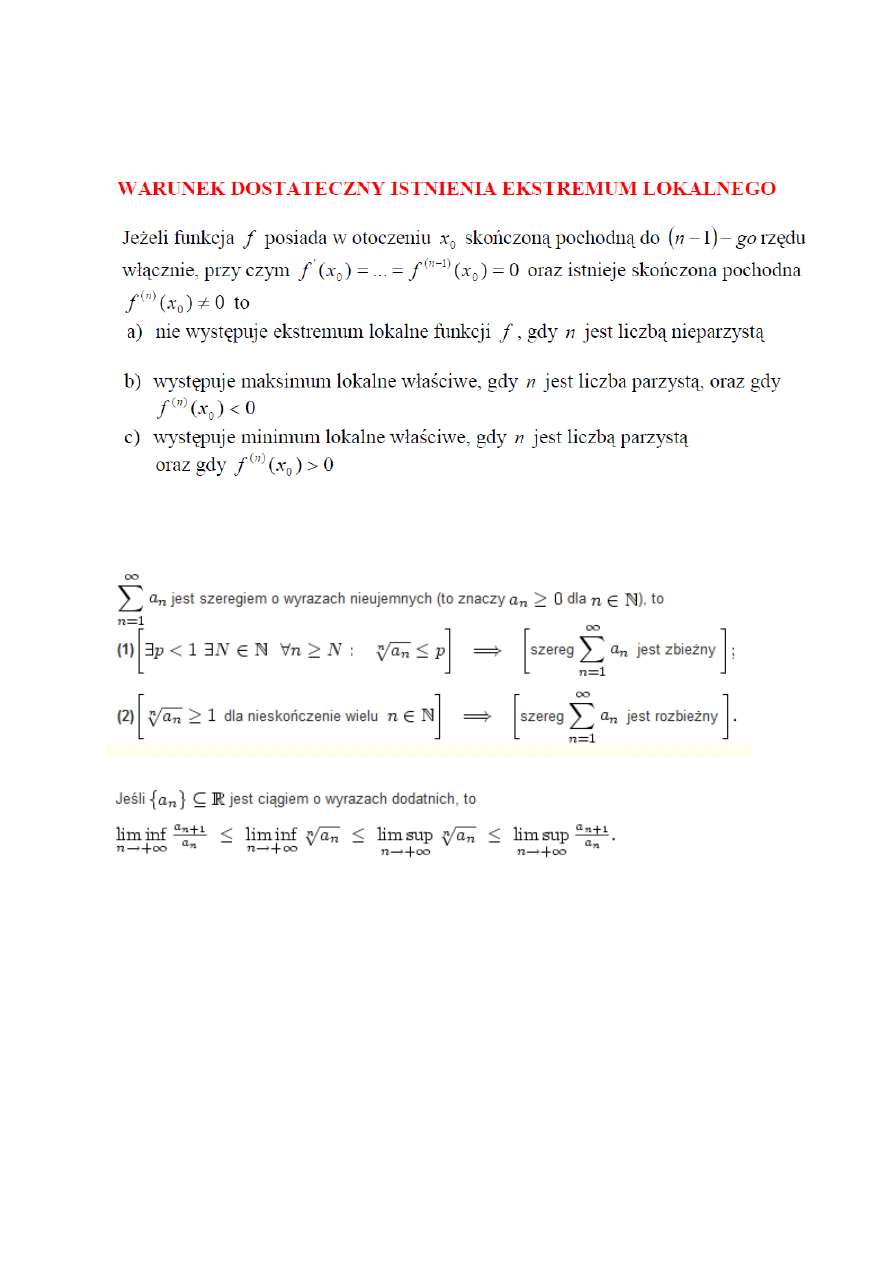
4) Udowodnić warunek dostateczny istnienia ekstremum lokalnego funkcji przy pomocy 
II pochodnej 
 

 

 
5) Badanie szeregów o wyrazach nieujemnych lub dodatnich.