Fizyka dla WIMiR 

Zestaw 6 (19.12.2011) 

Zadanie 1 

Proszę  wyprowadzić  wzór  na  moment  bezwładności  cienkiego  pręta  względem  prostopadłej  osi 
przechodzącej przez środek pręta oraz osi przechodzącej przez jego koniec. Pręt ma masę m i długość L. 

Zadanie 2 

Proszę wyprowadzić wzór na moment bezwładności cienkiej prostokątnej płyty o bokach a i b względem 

osi symetrii płyty. Płyta ma masę m. 

Zadanie 3 

Proszę wyprowadzić wzór na moment bezwładności cienkiej obręczy względem osi symetrii prostopadłej 
do jej płaszczyzny. Obręcz ma masę m i promień R. 

Zadanie 4 

Proszę wyprowadzić wzór na moment bezwładności cienkiego dysku względem osi symetrii prostopadłej 
do jego płaszczyzny. Dysk ma masę m i promień R. 

Zadanie 5 

Proszę wyprowadzić wzór na moment bezwładności cylindrycznej rury względem osi symetrii prostopadłej 
do płaszczyzny jej podstawy. Rura ma masę m, promień wewnętrzny R

1

 i promień zewnętrzny R

2

. Proszę 

następnie,  w  oparciu  o  wynik  wyprowadzenia,  podać  momenty  bezwładności  walca  oraz  powłoki 
cylindrycznej  względem  osi  symetrii  prostopadłych  do  płaszczyzn  ich  podstaw.  Walec  i  powłoka  mają 
jednakowe masy m i promienie podstawy R. 

Zadanie 6 

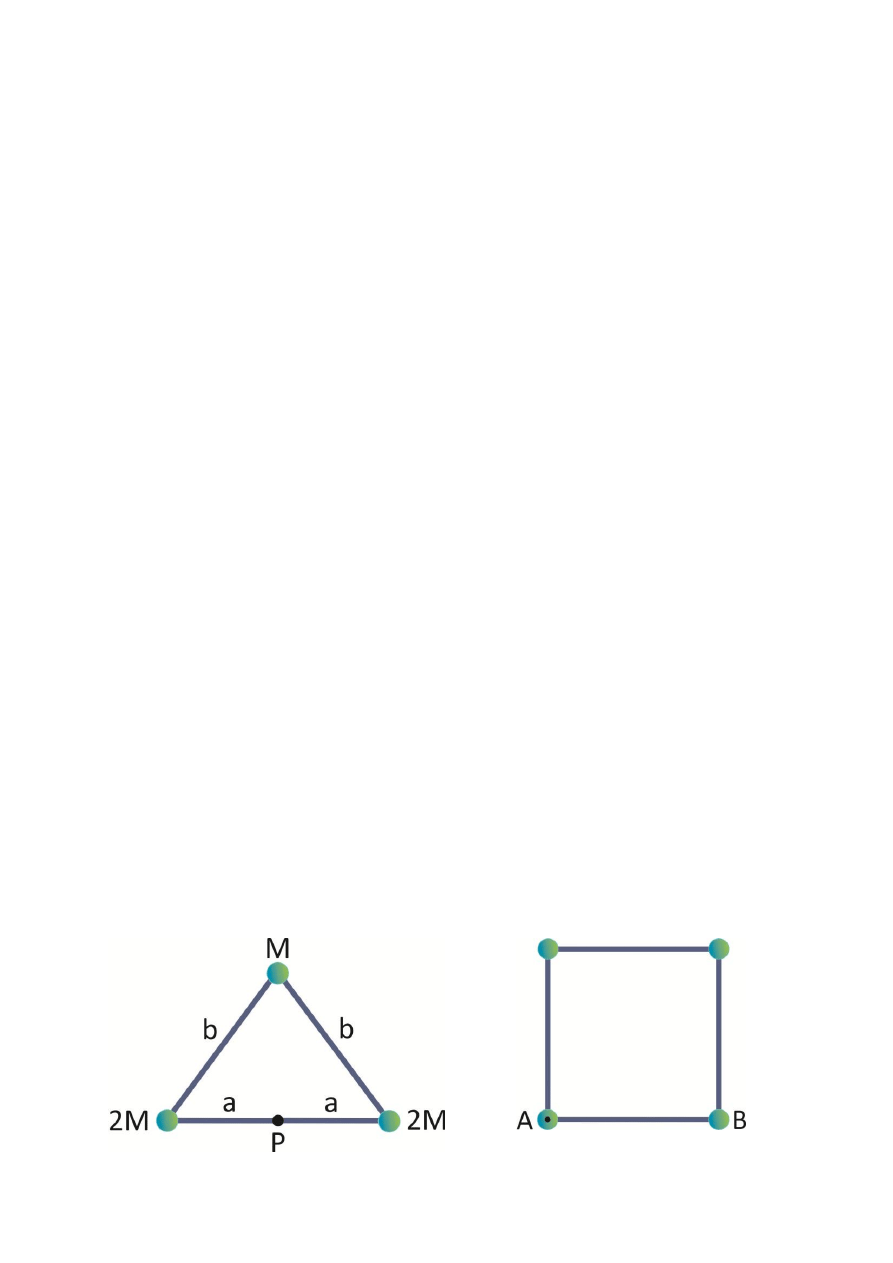
Przedstawione na rysunku ciało sztywne składające się z trzech kul połączonych prętami o znikomo małej 
masie  może  obracać  się  wokół  osi  prostopadłej  do  płaszczyzny  rysunku  i  przechodzącej  przez  punkt  P. 
Początkowo  ciało  pozostaje  w  spoczynku.  Proszę  obliczyć  pracę  potrzebną  do  nadania  temu  ciału 
prędkości kątowej równej 5 rad/s, jeśli wiadomo, że M = 0.4 kg, a = 30 cm i b = 50 cm. 

 

 

Zadanie 7 

Cztery kule o masach 0.2 kg umieszczone są w wierzchołkach kwadratu o boku 0.5 m i połączone prętami 
o  znikomo  małej  masie.  Otrzymane  tym  sposobem  ciało  sztywne  może  obracać  się  w  płaszczyźnie 
pionowej  wokół  osi  przechodzącej  przez  punkt  A  i  prostopadłej  do  płaszczyzny  kwadratu.  Początkowo 
ciało  utrzymywane  jest  w  spoczynku  w  położeniu  pokazanym  na  rysunku.  Proszę  wyznaczyć  moment 
bezwładności  ciała  względem  osi  przechodzącej  przez  punkt  A  oraz  jego  prędkość  kątową  w  chwili,  gdy 
pręt AB przechodzi przez położenie pionowe.